RDP 9313: The Determinants of Corporate Leverage: A Panel Data Analysis 4. Results
December 1993
- Download the Paper 105KB
4.1 Estimation Issues
We estimate the model of leverage using a balanced sample of 105 firms, each of which has data for the entire period from 1973 to 1990.[11] Results from the larger, unbalanced panel of firms are reported in Appendix 2.
Our model of leverage can be estimated in several ways. The appropriate technique depends upon the structure of the error term, uit, and the correlation between the components of the error term and the observed determinants of leverage.
In the simplest case, in which there are no firm- or time-specific effects, μi = λt = 0, Ordinary Least Squares (OLS) is appropriate. However it might be expected that both unobservable firm-specific and unobservable time-specific factors will have an effect on leverage. For example, the managers of one firm may be consistently more risk averse than other managers and as a result, the firm that they manage may have consistently low gearing (μi<0). Similarly, changes in taxation regulations may make debt relatively more expensive in some years than in others and for some firms more than others. As a result, desired leverage would be lower in those periods and for those firms (λt, μi<0).
In estimating Equation 1, unobservable effects can be accommodated using one of two techniques. First, the unobservable effects can be included in the error term. The variance-covariance matrix of the resulting non-spherical errors must be transformed to obtain consistent estimates of the standard errors. In this case, the ‘random effects’ estimator is appropriate (Hsiao, 1989).
However, a problem arises with the random effects estimator if the unobservable effects, which have been included in the error term, are correlated with some or all of the regressors. For example, managers' risk aversion may cause them to invest in fewer positive net present value projects and thus slow the growth of their firm. This would imply that the omitted variable measuring risk is correlated with both leverage and growth. This simultaneity would make the random effects estimator inconsistent. As a consistent alternative to the random effects estimator, a dummy variable can be included for each firm. This estimation approach, known as ‘fixed effects’, yields consistent estimates regardless of correlation between firm-specific error components and the regressors. However, it is less efficient than the random effects estimator. The inefficiency arises because the fixed effects estimator requires a separate parameter to be estimated for each firm in the sample in place of the single variance estimate that is required for the random effects estimator.
The above discussion of the random and fixed firm effects applies equally to the random and fixed time effects. The same techniques are also appropriate.
Before we discuss parameter estimates, two questions are addressed. First, is there evidence of individual and time effects? Second, if these effects exist, are they correlated with the observable regressors?
There are a number of ways in which we can examine the importance of the firm and time effects. First we test the joint significance of the firm and/or the time dummy variables in the fixed effects specification.[12] These tests, reported in Table 1, point to the existence of both firm and time effects.
| Null Hypothesis |
Test Statistic |
Statistic Distribution |
P-Value | |
|---|---|---|---|---|
| Time Intercepts | λt=0, ∀ t=1..T |
2.25 | F16,1658 | 0.003 |
| Firm Intercepts | μi=0, ∀ i=1..N |
31.07 | F104,1658 | 0.000 |
The fixed firm and time effects specification only includes the firm dummy variables, the time dummy variables and those variables that vary over both firms and time, Xit. The variables that vary only over time, Zt, are linear combinations of the time dummy variables and the variables that vary only over firms, Wi, are linear combinations of the firm dummy variables. This perfect collinearity prevents us from being able to incorporate Zt and Wi in the fixed firm and time effects specification.
Given that both the firm and the time effects are significant at the 5 per cent level, the interesting question becomes, can the information in these effects be more parsimoniously captured by our variables that vary only over firms or only over time? More specifically, can our firm dummy variables be replaced by the industry and listing dummy variables without a loss of explanatory power? Likewise, can the time dummy variables be replaced by our macro-economic variables? It turns out, as shown in Appendix 4, that replacing the T (N) time (firm) dummy variables with the Kz (Kw) variables that vary only over time (firms), implies a set of T-Kz (N-Kw) linear restrictions on the coefficients of the time (firm) dummy variables. These restrictions can be tested by comparing the residual sums of squares of the restricted and unrestricted models in the usual manner. Table 2 reports these tests on the firm and time effects.
| Test Statistic | Statistic Distribution | P-Value | |
|---|---|---|---|
| Time Intercepts vs the Macro-economic Variables | 1.55 | F13,1658 | 0.09 |
| Firm Intercepts vs the Industry and Listing Dummy Variables | 21.23 | F98,1658 | 0.00 |
| Note. 1. The null hypotheses are expressed in full in Appendix 4. |
|||
At the 5 per cent level, we cannot reject the restrictions that are required to validly replace the time dummies with the macro-economic variables. This suggests that, after allowing for the effects of the variables that vary over both firms and time, the macro-economic variables explain most of the residual variation in leverage, over the time dimension. In contrast, the restrictions implied by replacing the firm dummy variables with the industry and the listing dummy variables are rejected. This rejection implies that the industry and listing dummy variables do not have rich enough structures to adequately describe the unobserved firm-specific factors (firm risk and management risk aversity, effective marginal tax rates and investment opportunities etc.).
In summary, these two sets of F tests indicate that the fixed firm effects specification (which includes the macro-economic variables – the real asset price, consumer price inflation and the differential between the real cost of debt and the real cost of equity) is the most parsimonious and informative fixed effects specification.[13]
To examine the issue of whether or not the firm effects are uncorrelated with the regressors, we use the Hausman (1978) specification test. This test rejects exogeneity in the random effects model at the 5 per cent significance level.[14] In a comparison of the fixed and random effects models where time effects are also included, the Hausman statistic also rejects the null hypothesis of exogeneity.[15] As a result, we prefer to focus on the fixed effects estimates. For comparison, we still present estimates using the random effects estimator.
4.2 Estimation Results
The results of estimating the leverage equation are reported in Table 3. We present results using a range of different estimators. The estimates in the second column are from the OLS estimator with no firm or time effects. The third column presents the fixed firm effects estimates while the results in the fourth column include both firm and time fixed effects. Finally, the random effects estimates are included in the last two columns. The results are generally consistent with our a priori expectations, outlined in Section 2.4, and suggest that firm, institutional and macro-economic factors combine to affect capital structure decisions.
| Variables | Series Mean | OLS | Fixed Effects: Firms | Fixed Effects: Firms and Time | Random Effects: Firms | Random Effects: Firms and Time |
|---|---|---|---|---|---|---|
| Constant | 1.00 | 5.44 (5.71) |
0.49 | 3.25 | −4.18 | −6.50 |
| Cash Flow | 14.36 | −0.36 (0.14) |
−0.17 (0.09) |
−0.18 (0.09) |
−0.18 (0.06) |
−0.18 (0.06) |
| Firm Growth | 8.79 | 0.06 (0.01) |
0.03 (0.01) |
0.03 (0.01) |
0.03 (0.01) |
0.03 (0.01) |
| Real Tangible Assets | 78.18 | 0.23 (0.03) |
0.11 (0.03) |
0.11 (0.03) |
0.12 (0.02) |
0.10 (0.01) |
| Firm Size | 7.70 | 2.88 (0.44) |
5.60 (0.86) |
5.46 (0.89) |
5.35 (0.26) |
5.91 (0.19) |
| Potential Debt Tax Shield | 10.07 | 0.36 (0.15) |
0.13 (0.11) |
0.15 (0.11) |
0.15 (0.07) |
0.16 (0.07) |
| Tax Exhaustion | 0.08 | 5.06 (2.41) |
4.70 (1.64) |
4.71 (1.64) |
4.78 (1.04) |
5.27 (1.04) |
| Real Asset Prices | 0.98 | 5.41 (2.08) |
2.48 (1.56) |
– | 3.17 (1.10) |
2.60 (1.30) |
| CPI Inflation | 9.83 | 0.14 (0.17) |
0.12 (0.13) |
– | 0.12 (0.16) |
0.12 (0.20) |
| Fund Cost Differential | −15.96 | 0.20 (0.12) |
0.10 (0.08) |
– | 0.10 (0.08) |
0.11 (0.11) |
| Mining | 0.16 | −1.37 (1.76) |
– | – | −3.43 (3.02) |
−3.40 (3.00) |
| Wholesale | 0.06 | 20.93 (2.35) |
– | – | 20.25 (4.75) |
20.23 (4.72) |
| Retail | 0.05 | 3.62 (1.04) |
– | – | 3.85 (5.12) |
3.81 (5.08) |
| Service | 0.14 | 10.10 (1.56) |
– | – | 9.24 (3.19) |
9.24 (3.16) |
| Conglomerate | 0.02 | 15.37 (3.19) |
– | – | 8.32 (7.93) |
8.55 (7.87) |
| Unlisted | 0.24 | 9.02 (1.28) |
– | – | 9.65 (2.57) |
9.65 (2.55) |
| Notes. 1. Leverage, the dependent variable, has a mean of 53.45 per cent. 2. Numbers in parentheses are standard errors. 3. Newey West standard errors, calculated with 2 lags, have been reported for the OLS and fixed effects specifications. |
||||||
The estimated coefficient on cash flow is negative and significantly different from zero. The fixed firm effects model predicts that a 5 percentage point increase in a firm's cash flow, relative to its total assets, will induce a 1 percentage point decline in its leverage, other factors being held constant.
This finding is consistent with other studies including Chaplinsky and Niehaus (1990), Titman and Wessels (1988), Kester (1986) and the management survey by Allen (1991). It is also consistent with the predictions of the financing hierarchy models described in Section 2.2. The importance of cash flow (the availability of retained earnings) in determining leverage may reflect the agency/financial distress costs of using external finance.
Other factors may also be responsible, in part, for the preference for internal finance. These include the need to maintain financing flexibility and the desire to minimise the flow of information to outsiders. Also firms may prefer internal finance because it reduces monitoring by the marketplace, and because it prevents dilution of existing stockholder claims. A reliance on internal funds may also reflect the inability of some firms to access external capital markets. All of these factors potentially explain the negative coefficient on the cash flow variable in our leverage equation.
The coefficient on the firm growth variable is also significantly different from zero and it has a positive sign. Its magnitude indicates that a 33 percentage point increase in growth is required to induce a 1 percentage point rise in leverage. Thus, differences in the predicted leverage of firms with growth rates within the ‘usual’ 5 to 10 per cent band tend not to be driven by firms' growth rates. However, some firms in our sample experienced massive growth or shrinkage over the sample period. For these firms, growth could explain up to 15 percentage points of the variation in corporate leverage.
The positive relationship between leverage and firm growth is consistent with the view that rapid growth exhausts firms' internal fund reserves. This may result in increased dependence on debt, the next least expensive fund source. In this light, the positive coefficient on firm growth is consistent with a fund cost hierarchy.
Alternatively, assuming that past growth is an adequate proxy for future prospects, the positive coefficient on firm growth may reflect creditors being far sighted enough to lend in anticipation of higher future cash flows. However, this view is contrary to the arguments found in the agency cost literature that suggest that rapidly growing firms are not able to use their growth potential as collateral against which loans can be secured. Agency cost theories also suggest that firms in growing industries have greater flexibility in their choice of investments and, thus, equity holders have greater freedom to expropriate wealth from bondholders. Again this increases the agency costs of debt and creates a negative relationship between leverage and growth. Hence, our evidence conflicts with these aspects of the agency cost view of financial structure.
The coefficients on the real tangible assets variable and firm size variable are both positive and significantly different from zero. This is consistent with the view that there are various costs (agency costs and expected bankruptcy/financial distress costs) associated with the use of external funds and that these costs may be moderated by size and collateral. Large firms often have more diversified operations and longer operating and credit histories. Likewise, firms with high quality collateral can obtain debt at lower premiums because of the greater security for creditors.
The ratio of real tangible assets to total assets is also significant in an economic sense. A 10 percentage point increase in real tangible assets, relative to total assets, is required to increase leverage by 1 percentage point. Given the possibility that real tangible assets vary between 0 and 100 per cent of firms' assets, our measure of ‘quality collateral’ is capable of explaining up to 10 percentage points of the cross-sectional variation in leverage predicted by our fixed firm effects model.
The coefficient on firm size is more difficult to interpret. Because we have taken the natural log of real total assets, percentage change comparisons cannot easily be made. Instead we observe that as real assets increase, so does predicted leverage but at a diminishing rate. The leverage of a firm worth 100 million dollars is expected to be 3.8 percentage points higher than the leverage of a firm worth 50 million dollars.[16] In comparison, the leverage of a firm with 250 million dollars is expected to be only 1.2 percentage points higher than a firm worth 200 million dollars. In our balanced sample, firms' real assets vary between less than one million dollars to almost 13 billion dollars. Thus, firm size explains a significant proportion of the variation in corporate leverage within our balanced panel.
The coefficient on the potential debt tax shield variable is insignificant, suggesting that we have been unable to detect a role for the tax system in determining corporate leverage. In comparison, the tax exhaustion dummy variable has a positive and significant coefficient. Its significance suggests that the distortions caused by the tax system are more important to firms that are tax exhausted. The coefficient estimate of 4.70 implies that, for the observations where the potential debt tax shield is unobservable, the mean effect of the tax distortion is to increase predicted leverage by 4.70 percentage points.
The results in Table 3 suggest a relatively unimportant role for the macro-economic variables over the full sample. However, in Appendix 3, the split sample results suggest that the real asset price index is important following financial deregulation. Asset prices are strongly significant in the post-deregulation period whereas, in the pre-deregulation period, asset prices are insignificant. In this light, it would appear that the pooled results, in Table 3, under-estimate the role of asset prices in the post-deregulation period and over estimate the role of asset prices in the pre-deregulation period. Based upon the estimated asset price coefficient, movements in asset prices between 1982 and 1988 explain 34 per cent of the average movements in leverage over the same period.
The insignificance of the consumer price inflation variable suggests that general goods price inflation has played little independent part in the trend towards higher leverage over the sample period. This may be because creditors are able to compensate themselves for the wealth transfer to debt holders created by inflation through increases in nominal interest rates. The issue is confused, however, by the fact that the periods of highest inflation coincided with the presence of financial controls which limited the ability of firms to respond with increased leverage.
The fact that the aggregate fund cost differential fails to add explanatory power to our model may reflect the difficulty in accurately measuring the relative costs of debt and equity rather than the unimportance of relative funding costs.[17]
The insignificance of the fund cost differential can also be understood in the context of financial deregulation. Prior to deregulation nominal equity costs were able to incorporate inflationary shocks. In contrast, interest rate controls prevented inflationary shocks from being built fully into nominal interest rates. Thus, the increase in inflation in the mid 1970s reduced the real cost of debt while leaving the real cost of equity relatively unaffected. Firms were prevented from taking advantage of the relatively low real interest rates by the controls placed on monetary growth. Hence, the credit rationing caused by financial regulations partially severed the anticipated relationship between relative fund costs and financial structure.
Following deregulation, the equity cost and the debt cost could adjust to inflation shocks. This flexibility caused the fund cost differential to stabilise. However, in the period following deregulation, firms were increasing their gearing in response to a wide variety of other influences. This behaviour made it more difficult to identify any relationship between our measure of the fund cost differential and corporate leverage.
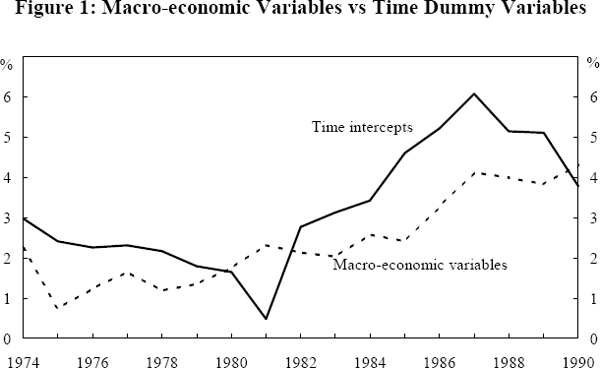
It is interesting to compare the estimated effect on leverage of the three macro-economic variables with the estimated coefficients on the time dummy variables. Figure 1, below, shows both the time effect coefficients (the black line) and the combined impact of the macro-economic variables (the grey line). The impact of the macro-economic variables is estimated as follows:
The constant term, α, is included to make the predicted impacts on leverage, from the macro-economic variables, directly comparable with the estimated time intercepts.
The tests presented in Table 1 reject the hypothesis that, if the macro-economic variables are excluded, the time dummy variables are insignificant. This finding is supported by the profile of coefficients on the time dummy variables shown in Figure 1. This profile suggests that significant variation in the time dimension is not explained by the variables that vary over both firms and time, Xit. We argued, based upon the tests reported in Table 2, that replacing the time dummy variables with our macro-economic variables, Zt, did not cause significant deterioration in the fit of the fixed effects model while improving the parsimony of the model. This finding is borne out in Figure 1 which shows that relatively high impacts on leverage from the macro-economic series coincide with high coefficients on the time dummy variables. However, it is also apparent that the macro-economic series do not capture some of the more subtle features of the evolution of corporate leverage.
Most clearly, the macro-economic variables fail to capture the move towards equity finance during the resources boom of the late 1970s and very early 1980s (See Lowe and Shuetrim, 1992, p. 14). Credit rationed firms, facing risky projects, concentrated in the primary resources sector, turned to external equity with the result that, even though asset prices were increasing, leverage fell.
During the 1980s the picture is somewhat different. Firms were more easily able to access debt finance to accumulate assets. Rising asset prices increased the perceived collateral of firms, increasing their demand for funds and increasing the financial sector's willingness to supply those funds. This change in the relationship between asset prices and leverage is made clear in Appendix 3 where we report estimates from the fixed firm effects model for the pre-deregulation part of our sample and for the post-deregulation part of our sample. The coefficient on real asset prices is insignificant when estimating with the sub sample that runs from 1974 to 1981. This supports the view that, prior to deregulation, rising asset prices simply led to a lengthening of the queue of borrowers. The coefficient becomes positive and significant when estimating using the sub sample from 1982 to 1990, supporting the view that financial deregulation removed the constraints on credit supply, enabling a more direct link from asset prices to credit.
Also, the macro-economic variables do not fully capture the turnaround in leverage in the late 1980s that is suggested by the profile of the time dummy variable coefficients. In part, this reflects the fact that there had been no generalised fall in asset prices by the end of our sample, yet there was rising concern in the business community, in the late 1980s, about high debt levels. It may also reflect the fact that the macro-economic variables do not incorporate the effects of changes in the tax system, which were occurring from 1985 onwards. The impacts on the effective tax rates of firms and the potential tax advantages of debt are not measured among our macro-economic variables, except in as much as the real cost of debt is measured after tax.
Coefficients on the industry dummy variables have been estimated using the OLS and the random effects approach. They cannot be estimated within the fixed effects framework because they are linear combinations of the firm dummy variables. The coefficients estimated for the OLS model are inconsistent because the firm effects have been incorrectly omitted. They are also likely to be inconsistently estimated for the random effects models given our a priori belief that the industry dummy variables are correlated with the unobserved determinants of leverage. More specifically, we feel that the industry dummy variables are correlated with the risks of financial distress that are captured by the firm effects (Lowe and Shuetrim, 1992). Also, the Hausman tests in Section 4.1 suggest that the random effects model may be inconsistently estimated because of endogeneity in the variables that vary over both firms and time.[18]
Instead of relying on inconsistent estimates of the industry effects, the average intercept terms for each of the firms (estimated from the fixed firm effects model) have been plotted in Figure 2. The firms are randomly ordered within each of the industry groups across the horizontal axis. The vertical axis is measured in percentage points of leverage explained by each firms' intercept term.
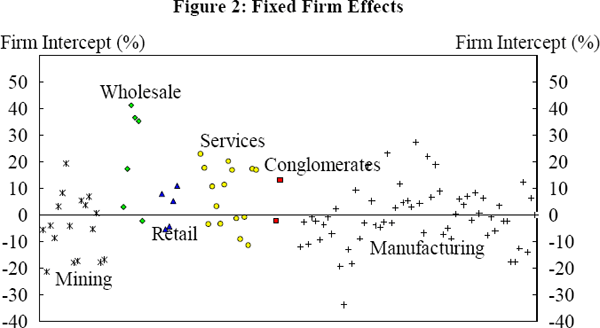
Figure 2 makes three points. First, even after controlling for other relevant and observed variables, mining and manufacturing firms do tend to have lower leverage than firms in the other industry groupings. This is consistent with the findings in Lowe and Shuetrim (1992) which suggest that firms in the wholesale, retail and service industries and conglomerates generally have higher leverage than do mining and manufacturing firms. Second, Figure 2 shows considerable variation within industry groupings that is not captured by the observed variables. Third, the individual effects are important, in an economic sense, relative to the observed variables. In some cases they dominate the explained components of leverage.
4.3 Specification Evaluation
4.3.1 Heteroscedasticity Tests
As a first step towards examining our specification, we calculated White tests for heteroscedasticity. In both the fixed firm and the fixed firm and time effects specifications, these tests reject the null hypothesis of homoscedasticity at the 5 per cent level which suggests that the residuals are non-spherical, even after allowing for firm and/or time effects.[19] The standard errors calculated for the OLS and fixed effects models take this heteroscedasticity into account.
4.3.2 Residual Autocorrelation Tests
Because of adjustment costs, firms may alter their financial structure slowly, as opportunities for new investments arise and as free cash flow becomes available to retire undesired debt. For this reason, a partial adjustment mechanism may well underlie movements in leverage over time.
To test the adequacy of the static specification, tests of the null hypothesis of no first or second order autocorrelation were conducted on the residuals from the fixed effects models. Only first and second order autocorrelation were considered because of our limited time dimension. In both cases, residuals were regressed on the independent variables from the original model and the first and second lags of the residuals. We tested the joint significance of the lagged residuals using Wald tests based upon White corrected variance-covariance matrices. These tests rejected the null hypothesis of no autocorrelation at the 5 per cent level.[20]
These rejections support the view that an autoregressive process is present in the error structure. For this reason, we report robust errors (which take into account both the heteroscedastic structure and the serial correlation in our residuals) for the OLS and fixed effects models in Table 3.
4.3.3 Tests for Non-linearities
As a final test of our static specification, we examine the validity of imposing a linear functional form upon our model of leverage. This is done within the broader context of the following general hypothesis:
where ut is a residual, Xt is the tth observation on
the regressors and ξt is a vector of other potential explanators
of the residuals. In this case, we replace the general term, ξt,
with (
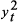 ,
,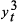 ,
,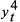 ), a series of powers
of the predicted values from the original model. A relationship between the
residuals and the powers of the predicted values can be interpreted as evidence
of non-linearity in the original
regression.[21]
Three tests are reported in Table 4 for each of the fixed effects models. For the
RESET 1 test, we regress the residual on a constant and the square of the predicted
value. For the RESET 2 test we also include the cube of the predicted value
and for the RESET 3 test we also include the fourth power of the predicted
value. The null hypothesis in each test is that the regressors explaining the
residuals are jointly insignificant.
), a series of powers
of the predicted values from the original model. A relationship between the
residuals and the powers of the predicted values can be interpreted as evidence
of non-linearity in the original
regression.[21]
Three tests are reported in Table 4 for each of the fixed effects models. For the
RESET 1 test, we regress the residual on a constant and the square of the predicted
value. For the RESET 2 test we also include the cube of the predicted value
and for the RESET 3 test we also include the fourth power of the predicted
value. The null hypothesis in each test is that the regressors explaining the
residuals are jointly insignificant.
| Tests | Distribution | Fixed Firm Effects | Fixed Firm and Time Effects | ||
|---|---|---|---|---|---|
| Test Statistic | P-Value | Test Statistic | P-Value | ||
| RESET 1 | 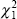 |
0.67 | 0.41 | 0.20 | 0.65 |
| RESET 2 | 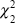 |
1.58 | 0.45 | 4.14 | 0.13 |
| RESET 3 | 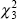 |
1.60 | 0.66 | 5.49 | 0.14 |
Wald tests of the joint significance of the regressors explaining the estimated residuals are reported. They have been calculated using the robust variance-covariance matrices which take into account both heteroscedasticity and autocorrelation. The tests fail to reject the null hypotheses at the 5 per cent level of significance. This supports the decision to adopt a simple linear relationship between leverage and its hypothesised determinants.
We also applied RESET tests to the full sample (which included firms with negative book values of equity in some periods and firms which made losses that were greater than 50 per cent of their end of period value). In this full sample, all of the RESET tests rejected the null hypothesis at the 1 per cent level. This finding suggests that the RESET tests do have power. It also supports our decision to omit the firms with negative book values of equity, or with massive losses which cut our sample from the available 224 firms to 209 firms. In the balanced sample, 5 firms were excluded on this basis.
4.3.4 The Dynamics of Leverage
To investigate the dynamic aspects of leverage, suggested by the presence of autocorrelation, we consider a single lag of the dependent variable. This primitive specification is adopted because of the relatively short time dimension in our panel. The model is estimated in differences to eliminate the fixed firm effects. We do not address the issue of non-stationarity in the leverage series, because, ignoring the exceptional cases where firms have negative equity, the book value of leverage is bounded between zero and unity.
An instrumental variable estimator is used to consistently estimate the parameters of the dynamic model (Hsiao, 1989).[22] This technique, unlike maximum likelihood estimation, is independent of the assumptions made about initial conditions. The results from the dynamic specification are reported in Table 5.
| Variables | Fixed Effects: Firms |
|---|---|
| Leverage−1 | 0.80 (0.27) [0.00] |
| Cash Flow | −0.17 (0.05) [0.00] |
| Firm Growth | 0.03 (0.01) [0.01] |
| Real Tangible Assets | 0.06 (0.03) [0.02] |
| Firm Size | 3.73 (2.45) [0.06] |
| Potential Debt Tax Shield | 0.03 (0.07) [0.35] |
| Tax Exhaustion | 1.78 (0.95) [0.03] |
| Real Asset Prices | −2.67 (1.93) [0.08] |
| CPI Inflation | −0.09 (0.10) [0.19] |
| Fund Cost Differential | −0.02 (0.11) [0.44] |
| Notes. 1. The numbers in round parentheses are standard errors. 2. The numbers in square brackets are p-values. |
|
The coefficient on the lagged dependent variable is significantly different from zero, supporting the view that leverage adjusts slowly to exogenous shocks. The speed of adjustment coefficient suggests that only 60 per cent of the full impact has been felt after 4 years. This estimate is fairly imprecise, however, and is not particularly robust to small changes in our specification. For example, the dynamic model estimated using the unbalanced panel of firms suggests that leverage is an explosive series. Given that leverage is bounded between zero and unity, this would appear difficult to support. In summary, our findings are consistent with the view that transaction costs are an important aspect of financial structure. However, further work is required to obtain precise estimates of the speed of adjustment.
The estimates reported for the dynamic model are qualitatively similar to those obtained from the static specification. The signs on the significant coefficients do not change (except for the coefficient estimate on the real asset price series which becomes insignificant at the 5 per cent level). Nevertheless, it is clear that further work towards an improved specification is required, especially in relation to the nature of the dynamic relationships involved.
Footnotes
Only 105 of the 110 firms with complete data are used because five had negative equity in some years or made losses that were greater than fifty per cent of their end-of-period total assets. These firms were treated as outliers. We also only estimated over the time interval from 1974 to 1990 because the 1973 data was used in calculating firms' growth rates. [11]
Baltagi and Chang (1992) conducted Monte Carlo experiments which suggested that F-tests of the firm intercepts and the time intercepts perform well in finite samples. [12]
The importance of the firm and time effects was also examined in the random effects framework. This was done by testing whether the variance of the firm error component and/or the variance of the time error component were significantly different from zero. We performed tests devised by Breusch and Pagan (1980), Honda (1985), Baltagi and Chang (1992) and Moulton and Randolph (1989). These all indicated that the firm effects were an important aspect of the specification. They were more mixed in their analysis of the time effects. The two-sided Breusch Pagan test rejected the null hypothesis while the one-sided Honda and Moulton and Randolph tests both failed to reject the null hypothesis. [13]
The test statistic is 28.82 and it has a
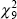 distribution under the null hypothesis.
[14]
distribution under the null hypothesis.
[14]
The test statistic is 48.47 and it has a
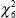 distribution under the null hypothesis.
[15]
distribution under the null hypothesis.
[15]
Firms' assets are valued at 1990 prices. [16]
See Appendix 1 for a description of the construction of these aggregate cost estimates. [17]
Hausman and Taylor (1981) suggest a consistent instrumental variable estimator which can be used to estimate the coefficients on the endogenous industry dummy variables using the firm averages of the Xit regressors as instruments. However, this technique is dependent upon the Xit regressors being exogenous with respect to the error components. [18]
For the fixed firm effects model, the Wald test statistic is 590 while the LM test
statistic for the fixed firm and time effects model is 489. These two statistics
are distributed
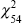 and
and
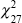 respectively under the null hypotheses.
[19]
respectively under the null hypotheses.
[19]
For the fixed firm effects model the statistic was 490. For the fixed firm and time
effects model, the test statistic was 494. Both statistics are
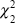 under the null hypothesis.
[20]
under the null hypothesis.
[20]
This form of the general hypothesis is known as the Regression Specification Error Test (RESET) (Ramsey, 1969). [21]
The second lag of the dependent variable and the second lagged difference in leverage are used as instruments for the lagged difference in leverage (Hsiao, 1989). [22]

