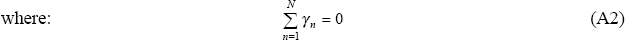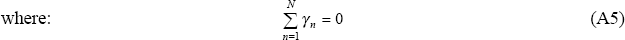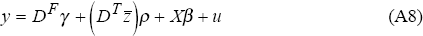RDP 9313: The Determinants of Corporate Leverage: A Panel Data Analysis Appendix 4: Testing The Firm and Time Specific Variables

In a panel data context, the time dummy variables are perfectly correlated with the observed variables that vary only over the time dimension. It is of interest to determine whether the variables that vary in the time dimension only, can adequately describe all of the variation in the dependent variable that is captured by the time dummy variables.

In an OLS regression model, using data with a single dimension, one would test this hypothesis by comparing the residual sum of squares from a general model in which all variables were included with the residual sum of squares from a restricted model in which the restriction had been incorporated. However, in our panel data framework, formulating the general model is not possible because of the perfect collinearity between the variables of interest.

In the following analysis, we show that the restricted model, which includes the variables that vary only across time but excludes the time dummy variables, is nested within the model that includes only the time dummy variables. In moving from the general model to the restricted model, we are enforcing a set of linear restrictions on the coefficients of the time dummy variables. Thus, we are still able to compare the residual sums of squares from the restricted and unrestricted models in the usual fashion. The problem described above extends simply to the case where the firm dummy variables are being replaced by variables that vary only across firms.

The proof that the models of interest are nested is as follows.

Stacking the observations by firm within each time period, the ‘unrestricted’ fixed firm and time effects model can be written as:

D^F = e_T ⊗ I_N is the (NT×N) matrix of firm dummy variables and 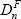is the nth firm dummy variable;

D^T = I_T ⊗ e_N is the (NT×T) matrix of time dummy variables and 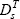is the sth time dummy variable;

e_s is a (S×1) vector of ones;

y is the (NT×1) vector representing the dependent variable;

X is the (NT×K) matrix of observed variables which vary over both firms and time;

u is the (NT×1) vector of residuals and

γ, δ and β are parameter vectors.

Alternatively, by dropping the intercept term, the normalisation restriction on the time dummy variable coefficients can be omitted. This reparameterisation of the ‘unrestricted’ model can be done without loss of generality.

The ‘restricted’ specification involves replacing the T time dummy variables with K_z variables that vary only over time, Z.

where ρ is the coefficient vector on Z. We can rewrite Z as a set of K_z linear combinations of the time dummy variables.

Where 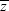is the (T×K_z) matrix containing the unique elements of Z. Hence, we can rewrite the ‘restricted’ specification in terms of the time dummy variables.

Comparing equation A4 and equation A6, the linear restrictions implicit in the ‘restricted’ model can be represented as:

This relation involves T restrictions, each repeated N times. The T unique restrictions can be written as:

To represent this set of linear restrictions in the standard form, ‘Rβ=r’, ρ must be eliminated. This involves projecting δ and 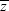ρ on 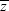to yield:

Hence, from equation A10 and A11:

Expressing in the Rβ=r form yields:

The orthogonal projection matrix 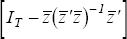has rank (T-K_z). Thus, moving from the unrestricted specification to the restricted specification involves T-K_z linearly independent, linear restrictions.

When replacing the N firm dummy variables by a set of K_w variables that vary only across firms, an analogous procedure can be used to show that N-K_w linearly independent, linear restrictions are implied.