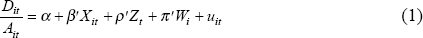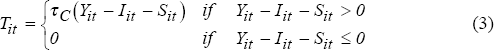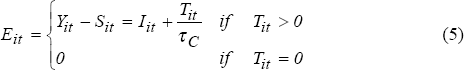RDP 9313: The Determinants of Corporate Leverage: A Panel Data Analysis 3. Empirical Model

The literature review suggests a number of factors that may influence financial structure. Some of these factors vary only across firms, while others vary only across time and still others vary across both firms and time. These variables are outlined below with more detailed definitions given in Appendix 1.

We assume a linear relationship between leverage and its determinants. That is:

where:

• leverage, our dependent variable, is firm debt, D_it expressed as a percentage of total assets, A_it. Both debt and total assets are measured at book value. Debt is measured as the difference between total assets and shareholders' funds.
• X_it is a vector of determinants that vary across both firms and time.
• Z_t is a vector of determinants that vary only over time.
• W_i is a vector of determinants that vary only across firms.
• α, β, ρ and π are vectors of coefficients that are assumed, in the standard model, to be constant over time and across firms.
• u_it is a composite residual comprised of a firm-specific component, μ_i, a time-specific component, λ_t, and a component that varies over both firms and time, v_it.

3.1 The Determinants of Leverage

3.1.1 Variables that vary across both firms and time: X_it

• Earnings before interest, tax and depreciation have been deducted, expressed as a percentage of total assets (Cash flow);
• The percentage growth in real assets (Growth);
• The natural log of real total assets (Size);
• Real tangible assets, measured as a percentage of total assets (Real tangible assets) and
• Income against which interest expenses can be offset, again expressed as a percentage of total assets (Potential debt tax shield).

To motivate the expected signs on these determinants of leverage, we draw upon our review of the literature. If firms face a fund cost hierarchy then cash flow should have a negative sign. As cash flow increases, more internal funds become available to firms, allowing them to reduce their reliance on more expensive debt funds. Likewise, firms facing a fund cost hierarchy are likely to have a positive relationship between leverage and their rate of growth. Higher growth rates are accompanied by greater demand for funds which will force firms to adopt external fund sources (debt first and then external equity). We also anticipate that an increase in real tangible assets, by increasing the quality of collateral, will lead to higher leverage. The coefficient on firm size is expected to have a positive sign because of the increased access to credit markets that is available to large firms. Finally, the potential income against which firms can offset their interest expenses (the potential debt tax shield) should have a positive sign because the gains from debt are reduced if interest cannot be deducted in the current period.

The precise definitions of these firm-related variables are given in Appendix 1. However, the complexity of the potential debt tax shield variable (denoted E_it hereafter) warrants further discussion. DeAngelo and Masulis (1980) and Titman and Wessels (1988) consider the relationship between non-interest tax deductions and the leverage of firms. They hypothesise that as these ‘non-debt tax shields’, S_it, increase, firms have less incentive to engage in debt financing for the purposes of tax minimisation. We take this a step further by recognising that firms focus on the amount of income that can be shielded from tax using interest payments, E_it. To determine this amount, one must first quantify the non-debt tax shields, S_it.

If the amount of tax paid by firm i in period t, T_it, is greater than zero then S_it can be obtained by working back from the expression for tax payable.

Thus, if a firm pays tax, the non-debt tax shields can be expressed as:

where Y_it is gross earnings, I_it is interest payments and τ_C is the corporate rate of tax. However, when firms pay no tax (ie., they are tax exhausted) we do not observe the extent to which non-debt tax shields plus interest payments exceed gross earnings. Thus non-debt tax shields are not observed. Because the earnings against which interest payments can be offset, E_it, are equal to gross earnings less non-debt tax shields, the following expression for E_it arises.

E_it, our measure of the potential debt tax shield, is unobserved when a company is paying no tax (i.e. is tax exhausted) because we cannot determine the relative proportions of income shielded by interest payments and by non-debt tax shields.

To allow for the fact that the potential debt tax shield is unobserved in some cases, firms' state of tax exhaustion is included as a regressor. It is a dummy variable that is set to one for all observations when the tax paid by a firm is equal to zero. This technique is referred to by Maddala (1977, p. 202) as the modified zero order regression method.

Given that the effects of the potential debt tax shield are always non-negative, we would expect a positive coefficient on the tax exhaustion dummy variable. Its value can be interpreted as the mean effect on leverage of the potential debt tax shields taken over all the observations with missing data.

3.1.2 Variables that vary only over time: Z_t

• Real asset prices;
• Consumer price inflation; and
• The differential between the real cost of debt and the real cost of equity where both costs are measured as aggregates for the Australian economy (Fund cost differential).^[9]

The expected signs on these variables are motivated by the discussion in Section 2 of the macro-economic influences on corporate leverage. We anticipate that increases in real asset prices will generate upward pressure on firms' demands for funds and, thus, raise leverage. Consumer price inflation should also have a positive relationship with debt if higher inflation increases the wealth transfer to debtors generated by the tax deductibility of nominal interest payments. Finally, we anticipate a negative sign on the fund cost differential variable because, as the relative cost of debt rises, profit maximising firms should tend to restructure their financing arrangements in such a manner as to reduce their debt dependence (leverage).

The summary of our literature review also highlights the importance of the effective rates of tax faced by firms. As Pender (1991) highlights, these effective tax rates depend upon five factors: (i) the tax status of shareholders, (ii) the non-debt tax shields associated with investment projects, (iii) earnings retention ratios, (iv) the rate of inflation and (v) the tax system. Because information is not readily available about investment projects or the tax status of shareholders, effective tax rates are not observed. Rather than deriving complicated approximations, we allow for time effects and individual firm effects which capture the influence of the major changes in the tax system (capital gains tax, dividend imputation and the steady reduction of corporate and personal tax rates).

3.1.3 Variables that vary only across firms: W_i

• Industry dummy variables;
• Listing category dummy variable.

We include these categorisation variables to pick up commonalities across industries and across listed and unlisted firms.

Many factors that influence individual firms' capital structure may be common within organisational structures and industrial groupings. Also many characteristics of firms may be reasonably similar within industry groupings but cannot be captured elsewhere. For example, industry classifications are strongly correlated with cash flow volatility; mining firms generally have more volatile earnings than firms in the service industry. Also, firms in the same industry often face common product and/or factor markets and are likely to have similar capital requirements and lumpiness of investment opportunities. For these reasons the industry classifications of firms are included in our specification. There is some previous support for the importance of industry groupings for capital structure decisions (Bradley, Jarrell and Kim, 1984).

The six broad industry classifications that we use are manufacturing, mining, wholesale trade, retail trade, services and conglomerates. To avoid perfect collinearity with the intercept term, the dummy variable representing the manufacturing firms (the largest category) is omitted.^[10]

Because listed firms are likely to have greater access to equity markets, we include a dummy variable that is set to one for all unlisted firms. This allows us to detect any differences in leverage between the listed and unlisted firms after allowing for the other observed factors.

Footnotes

We use the measure of the real cost of equity devised by Dews, Hawkins and Horton (1992). It is the sum of the average earnings yield and the ten year average growth rate in real non-farm gross domestic product. This is an approximate measure of the expected earnings prospects of firms after taking into account firms' current yields and the past growth of the economy (excluding the farm sector). [9]

Measures of the volatility of cash flow were also initially included in our specification. The various measures were insignificant. This may reflect the difficulty of obtaining an accurate measure of ex ante volatility of cash flow. An examination of macro-economic data indicates that particular sectors of the economy have considerably more volatile cash flows than other sectors. For this reason, our industry dummy variables may be capturing the effects of cash flow volatility on leverage. [10]