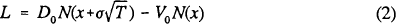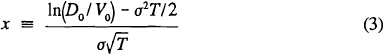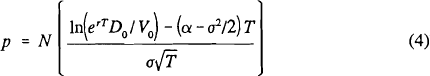RDP 9210: Contingent Claim Analysis of Risk-Based Capital Standards for Banks 2. Model

Define V_t as the market value of a bank's assets (the discounted value of earnings from those assets) and D_t as the value of the bank's deposits. For simplicity we assume that deposits are the bank's only liabilities, and that they are fully guaranteed and hence riskless. Interest on deposits accrues continuously at the riskfree rate, and is payable at some future date t=T. The bank makes decisions regarding asset risk and capital at the present (t=0), and is monitored by bank supervisors at date T.^[3] At the monitoring date T (and no sooner), the bank is declared insolvent if D_T > V_T; in that case, the deposit guarantor pays the depositors D_T and takes control of assets worth V_T, suffering a loss of D_T−V_T.

We assume that the value of bank assets follows a constant variance diffusion process:

where α > 0 is the instantaneous expected rate of return on assets, σ > 0 is the instantaneous standard deviation of the rate of return, and dz is the differential of a standard Wiener process.

2.1 The Contingent Liability of the Deposit Guarantor

Merton (1977) has shown that under the assumptions above the liability associated with the deposit guarantee can be evaluated using the Black-Scholes option pricing equation for put options. The expiration date of the implicit option provided by the deposit guarantor is date T, the next point at which the bank can be declared insolvent by supervisory authorities. The guarantor's liability at t=0, which we denote L, is:

where D₀ is the present value of deposits, V₀ is the present value of assets, N(•) denotes the standard normal cumulative density function, and x is defined as:

2.2 The Probability of Failure

As noted above, bank failure occurs in this model if the end-of-period value of assets V_T is less than the end-of-period value of deposits inclusive of continuously-compounded interest, D_T = e^rTD₀. As shown by Smith (1976, p. 15), the probability of failure, which we denote as p, can be written:

Assuming that the expected rate of return on bank assets equals or exceeds the riskfree interest rate, α ≥ r, the probability of failure satisfies the condition 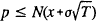. Thus, 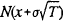is an upper bound on the probability of failure; we denote this upper bound as FP:

Footnote

We have assumed that the bank's deposits mature at the same point in time that the bank is monitored by authorities. This assumption simplifies the presentation of the model without substantial effect on the conclusions. [3]