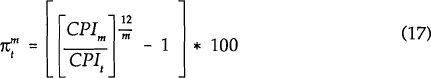RDP 9204: The Term Structure of Interest Rates, Real Activity and Inflation 4. The Yield Curve and Changes in Inflation
May 1992
- Download the Paper 439KB
4.1 The Mishkin Methodology.
The literature on the ability of the yield curve to predict changes in inflation typically begins with the standard Fisher equation:
where Et denotes the expectation at time t, 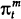 the
inflation rate between time t and m,
the
inflation rate between time t and m,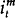 if the nominal
m period interest rate and
if the nominal
m period interest rate and 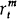 the real m period
interest rate.
the real m period
interest rate.
The observed rate of inflation (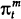 ) equals the expected rate plus a
forecast error:
) equals the expected rate plus a
forecast error:
Substituting (13) into (12) yields:
To obtain a relationship between the slope of the yield curve and the change in the inflation rate the n period inflation rate is subtracted from (14) yielding:
Mishkin (1990) assumes that the slope of the real yield curve is constant through time so that
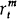 −
−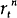 is a constant. Given the
additional assumption of rational expectations, the forecast errors cannot be forecasted given
information at time t. The dual assumptions of a constant real term structure and rational
expectations underpin the following equation which forms the basis of Mishkin's tests:
is a constant. Given the
additional assumption of rational expectations, the forecast errors cannot be forecasted given
information at time t. The dual assumptions of a constant real term structure and rational
expectations underpin the following equation which forms the basis of Mishkin's tests:
If prices are fully flexible and instantaneously adjust to changes in monetary policy, the assumption of a constant real rate spread is appropriate and β should equal one. The model presented in Section 2, however, shows that when such price flexibility does not exist, the slope of the real yield curve does change over time and the results in Section 3 suggest that these changes have real effects on the economy.
As Frankel and Lown (1991) argue, the assumption of a constant slope to the real yield curve is overly restrictive. Indeed, due to the existence of sticky prices, long term interest rates are more likely to accurately reflect inflationary expectations than short term rates. They argue that in an inflation change equation such as (15) the slope of the entire yield curve is likely to out-perform the spread between securities matching the period for which the change in inflation is being forecast. They develop a technique to obtain a summary measure of the slope of the yield curve using yields on securities of all maturities. Their technique is difficult to apply to Australian data due to the lack of data on yields on securities over a wide range of maturities. However, failure of the real interest rate spread to be a constant allows the possibility of superior forecasts of future changes in the inflation rate being generated by using a long-short spread compared to those generated by securities which match the period over which the change in inflation is being forecast.
4.2 Estimation Procedure and Data.
In the following tables, results are reported for the “Mishkin regressions” (that is, those using interest rate maturities which match the period over which the change in inflation is being forecast as in (16)) as well as for the less restrictive regressions where the spread between the 10 year bond rate and the 180 day bank bill is used to predict inflation. Two sets of estimates are presented for the Mishkin regressions. The first (Table 5) are Ordinary Least Squares results where the standard errors have been corrected for serial correlation and heteroskedasticity using the same procedure outlined in the previous section. The second set of results (Table 6) are obtained using the Seemingly Unrelated Regression (SUR) technique. The forecast errors from the equation for the change in inflation over the period m to n should be correlated with those from the equation for the change in inflation over the period i to n. The SUR technique uses the extra information contained in these correlations to obtain more efficient estimates.
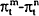 |
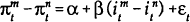 |
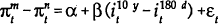 |
Nobs | ||||
|---|---|---|---|---|---|---|---|
| α | β |  |
α | β | 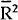 |
||
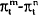 |
−0.18 (0.17) |
0.27 (0.55) |
−0.03 | −0.20 (0.20) |
−0.01 (0.07) |
−0.03 | 34 |
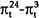 |
0.03 (0.55) |
0.46 (0.25) |
0.04 | −0.05 (0.49) |
0.47 (0.14) |
0.14 | 28 |
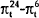 |
0.39 (0.43) |
0.76 (0.23) |
0.20 | 0.05 (0.37) |
0.48 (0.11) |
0.28 | 28 |
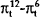 |
−0.15 (0.26) |
0.08 (0.08) |
−0.01 | 32 | |||
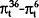 |
0.08 (0.26) |
0.53 (0.11) |
0.26 | 24 | |||
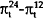 |
0.11 (0.21) |
0.42 (0.05) |
0.55 | 28 | |||
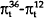 |
0.17 (0.14) |
0.50 (0.11) |
0.48 | 24 | |||
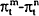 |
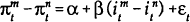 |
|
|---|---|---|
| α | β | |
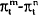 |
−0.09 (0.11) |
0.60 (0.46) |
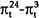 |
0.20 (0.54) |
0.65 (0.24) |
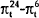 |
0.32 (0.42) |
0.69 (0.20) |
NOTES. |
||
The SUR standard errors have also been corrected to account the serial correlation induced by the overlapping observations[5]. SUR results are not reported for the equations estimated using the 10 year-180 day spread because they are identical to the OLS results as each equation has the same regressor. Other long-short spreads were examined, however the 10 year-180 day spread consistently proved superior. Mishkin regressions cannot be conducted for all horizons due to the lack of appropriate interest rates at certain maturities. The sample period runs from September 1982 to June 1991. This covers the period over which all government securities were issued by tender.
To estimate equation (16) as written, the price level needs to be observed at times t,
m and n. However, available price indices are for prices averaged over a period of
time and not prices at a particular point in time. For example the CPI for the June quarter
represents average prices over the months of April, May and June and not the level of prices at
the end of June. Accordingly, in estimating equation (16), the average of the three end-month
interest rates for the quarter is used in place of the end quarter interest rate. 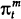 is
calculated as follows:
is
calculated as follows:
where CPIt is the Consumer Price Index (adjusted for Medicare changes) for the quarter ending at time t. The CPI data are taken from the Reserve Bank of Australia Database.
4.3 Results.
The results in both Tables 5 and 6 suggest that the slope of the yield curve provides no information about the change in inflation between 3 and 6 months. This is the case for both the 6–3 month spread and the 10 year-180 day spread. The Mishkin equations also perform poorly in explaining the change in inflation between two years and three months. Using the OLS estimates it is not possible to reject the hypothesis that the coefficient on the yield spread equals zero. In contrast, the hypothesis can be rejected using the SUR estimates. In both cases, however, the standard errors are relatively large making it difficult to distinguish between economically quite different hypotheses.
The spread between the two year bond rate and the 180 day bill does provide some statistically significant information about the change in inflation between six months and two years. Using both the SUR and OLS estimates it is possible to reject the hypothesis that the coefficient equals zero while it is not possible to reject the hypothesis that the coefficient equals one. The standard errors are once again relatively large making precise inferences difficult.
A comparison of the first and second blocks of Table 5 shows that the 10 year-180 day spread outperforms the “Mishkin” equations. Once one moves beyond the shortest period, the coefficient on the 10 year-180 day spread is generally significantly different from zero and is estimated more precisely than the comparable coefficients from the Mishkin equations. This long-short spread does best in explaining the difference between the inflation rate over the next year and the inflation rate over the next two years. In also does well in explaining the difference in the inflation rate over the next year and the inflation rate over the next three years. The results also suggest that the 10 year-180 spread provides little information about the change in inflation between six months and one year.
The failure of the slope of the yield curve to predict changes in inflation in the short run but its ability to predict changes in inflation in the medium run, is broadly consistent with international evidence[6]. It suggests that changes in the slope of the short end of the nominal yield curve reflect, to a substantial degree, changes in the slope of the real yield curve, largely brought about by the liquidity effects of monetary policy. The slope of the short end of the yield curve is thus a poor indicator of future changes in inflation.
If one accepts the expectations theory of the term structure, long term rates are not immune from the liquidity effects of monetary policy; however, the longer is the maturity the less important is the effect. Changes in long term interest rates thus more accurately reflect changes in inflationary expectations. The fact that the spread between the 10 year bond rate and the 180 day bill rate outperforms the spreads between the bill rate and both the two and five year rates supports this view. The greater accuracy of long term rates in measuring inflationary expectations allows the long-short spread to serve as an indicator of changes in inflation in the medium term. In the short run this spread is of limited use in predicting inflation because the bulk of the impact of expansionary monetary policy falls on output and not prices.
Footnotes
In a study of the US term structure for maturities less than 12 months, Mishkin (1990a) finds that for maturities of 6 months or less the term structure provides no information on inflation while for maturities of 9 to 12 months the term structure does provide some information. In a more comprehensive study of the “less than 12 months” term structure for a number of OECD countries, Mishkin (1991) finds little evidence that the term structure provides information about future changes in inflation. Examining the slope of the US yield curve between one and five years, Mishkin (1990b) concludes that at longer maturities the term structure can be used to assess inflationary expectations. Jorion and Mishkin (1991) provide similar evidence for a range of OECD countries. Browne and Manasse (1990), however, present conflicting evidence arguing that the inflation forecasting ability declines as the maturity lengthens. [6]



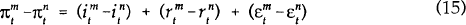
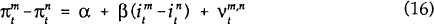
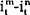 is the difference between the m period nominal
interest rate and the n period nominal interest rate at time t.
is the difference between the m period nominal
interest rate and the n period nominal interest rate at time t.