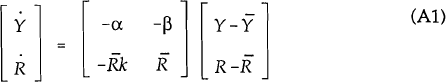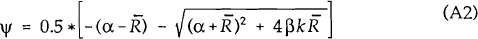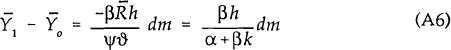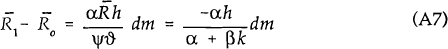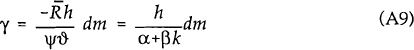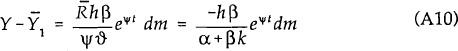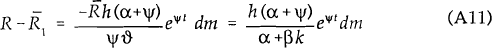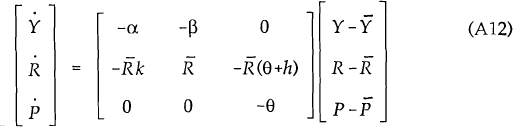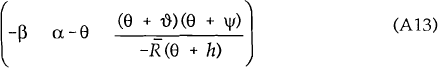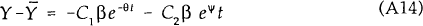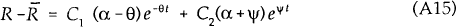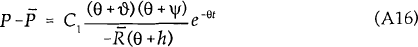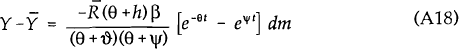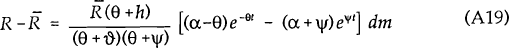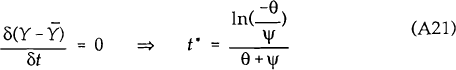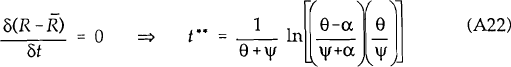RDP 9204: The Term Structure of Interest Rates, Real Activity and Inflation Appendix 2: Derivation of Dynamics

This appendix derives the equations of motion for the model presented in Section 2. As in Section 2, it begins with the model where prices are assumed fixed. To obtain an equation for 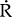in terms of γ and R first note that, with fixed prices, I=i and then substitute (5) into (1). Linearizing both the resulting equation and (4) around the steady state values 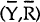, the system can be written as follows:

As the determinant of the above matrix is negative, the system has both a positive (ϑ) and a negative (ψ) root. The negative root is given by:

The characteristic vector associated with ψ, (x₁x₂) is such that:

The equations of motion along the saddle-path are thus given by:

where γ is a constant to be solved for.

Consider the change in the steady state values following a monetary expansion.

Initially (at time t=0), Y is fixed so that:

This implies that

Substituting this back into equations (A4) and (A5) gives the equations of motion along the saddle path.

Since |α| < |ψ|, both Y and R are less than their steady state values along the saddle path.

Now consider the system with flexible prices. Substituting (5) into (2) and then substituting the result and (4) into (1), the system can be written as follows:

This system has three roots, two of which are the same as the fixed price model (ψ and ϑ) while the third is −θ. The eigen vector associated with ψ is (−β α+ψ 0) while the vector associated with −θ is:

The equations governing the evolution of the system along the saddle path are thus given by:

where C₁ and C₂ are constants. From the steady state conditions, we know that in steady state changes in M leave Y and R unchanged and that 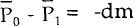. This implies that:

Given that C₁=−C₂, the equations of motion can be rewritten as :

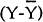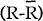As and are both the sums of declining exponentials, they both have at most one interior maximum/minimum. To find the time at which these extreme points occur, equations (A18) and (A19) are differentiated with respect to t and then solved for t^* (t^**). This yields:

The larger is θ, the quicker the output and interest rate responses reach their maxima. In the limit, as θ→∞, both t^* and t^** go to zero.