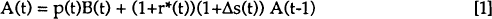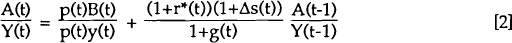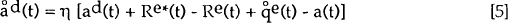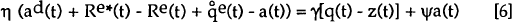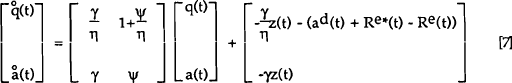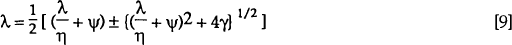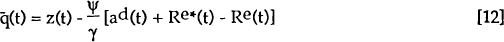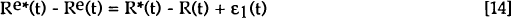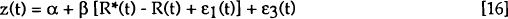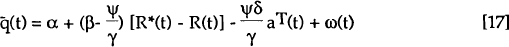RDP 9203: Real Exchange Rates and the Globalisation of Financial Markets 2. Real Exchange Rates and the Globalisation Process
March 1992
- Download the Paper 670KB
(a) Theoretical Model
The effects of financial liberalisation can be thought about in terms of balance of payments equilibrium. A reasonably precise statement of the balance of payments identity between two countries is:
where:
| A(t) | is bilateral net foreign assets measured in domestic currency in period t; |
| p(t) | is the price of output in period t; |
| B(t) | is the bilateral real balance of trade surplus in domestic currency in period t; |
| r*(t) | is the average nominal interest rate on bilateral net foreign assets in period t[2]; |
| s(t) | is the bilateral nominal exchange rate, domestic currency per unit of foreign currency, in period t. |
The inclusion of the nominal depreciation term is to capture valuation effects on the net interest component of the balance of payments and the stock of net foreign assets valued in domestic currency at the end of the previous period. It is convenient to divide both sides of [1] by nominal output, Y(t) = p(t)y(t):
Where g(t) is the growth rate of nominal GDP in period t. Defining a(t) to be bilateral net foreign assets as a share of GDP and b(t) as the nominal or real share of the bilateral trade balance in nominal or real GDP, the change in a(t) expressed now in continuous time is given by:
where 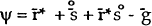
For simplicity, the net interest component of the balance of payments is always subsequently evaluated by replacing the average interest rate on net foreign assets; nominal exchange rate depreciation and the nominal growth rate in equation [3] with their steady-state values, indicated by a bar.
The bilateral trade surplus as a share of GDP is assumed to be given by:
where:
| q(t) | is the logarithm of the real exchange rate in period t; |
| z(t) | summarises exogenous real factors that affect domestic excess demand and foreign excess demand for domestic goods in period t. |
The final building block of the system is the capital account equilibrium condition. Capital flows adjust the actual stock of net foreign assets a(t) towards the desired stock, with a possible lag measured by η. The desired stock depends on the net return differential and the desired net stock of the foreign country's assets at a zero return differential[3].
where:
| ad(t) | is a variable reflecting the desired bilateral net foreign asset position as a share of GDP, when the rate of return differential is zero; |
| Re*(t) | is the exogenous expected foreign real interest rate in period t; |
| Re(t) | is the exogenous expected domestic real interest rate in period t; |
| the “d” superscript indicates the desired value of a variable and “e” denotes an expected value. | |
In equilibrium this collapses to the interest rate parity condition in real terms with allowance for a risk premium equal to ad(t) − a(t). Balance of payments equilibrium where the current account between the two countries is matched by desired capital flows is given by substituting equation [4] into equation [3] and setting it equal to desired capital flows in equation [5].
This together with equations [3] and [4] constitutes a simultaneous system of forward-looking differential equations that may be solved for the expected time paths of the endogenous variables q(t) and a(t). Assuming rational expectations, this system may be written as:
The characteristic equation is given by:
and the solution for λ is:
Given the positive sign restrictions on the coefficients, one eigenvalue λ is positive and one is negative. Choosing the negative value of λ, the solution for the time paths of the variables is:
The steady-state levels, shown with a bar, are solved by setting 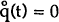 and
and 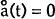 in
equation [7]. That is:
in
equation [7]. That is:
The steady-state value of q(t) in equation [12] could be the basis of cointegration tests concerning the long-run behaviour of the real exchange rate.
(b) Globalisation and Cointegration
Meese and Rogoff (1988), in following up their earlier paper on the out-of-sample forecasting properties of standard exchange rate models, investigated the associations between real exchange rates and real interest differentials by testing for cointegration between these variables. Their tests over the period 1974 to 1984 (using monthly data) suggested that these variables were not cointegrated, and the authors took this to imply that the relationship between the two variables was “at best tenuous”. A number of other authors using a variety of exchange rates and estimation approaches also support this view[4].
The failure to find cointegration between bilateral real interest differentials and bilateral real exchange rates over post-Bretton Woods sample periods may be related to the process of financial liberalisation. This process has reduced liquidity constraints between countries, permitting world financial capital to be reallocated from relatively high saving and low investment return countries towards those in the reverse situation. This may be represented in equation [12] by the way in which the behaviour of the exogenous variables is specified, i.e. the expected real interest differentials, the desired bilateral stock of net foreign assets at a zero real interest differential, and z(t) which represents exogenous variables influencing the domestic and foreign excess demand for domestic goods. The following assumptions are made:
-
financial liberalisation and globalisation does not imply goods market integration. In the
absence of perfect real factor mobility, the real interest differential is assumed to be a
non-stationary process of the form:
where ε1(t) is a random error term.
-
in the absence of capital controls, the desired net stock of another country's assets
(as a share of income) at a zero net return differential is assumed to be proportional to
the total net stock of foreign assets aT (as a share of income). That is, if the
return differential is zero, domestic residents will hold a fixed proportion δ of
their total net foreign assets aT in the assets of a given foreign country. The
fixed weight δ, for example, could be derived from an optimisation problem where
agents hold net foreign assets in proportion to the weight of the foreign country's
output in domestic consumption. Here aT is the cumulated current account surplus
vis-a-vis all other countries, and is assumed to be an exogenous non-stationary
process of the form:
Thus as financial liberalisation leads to non-mean-reverting movements in the overall net foreign asset position vis-a-vis the rest of the world as a share of GDP, all desired bilateral net foreign asset positions at a zero net return differential are affected.
-
domestic and foreign excess demand for domestic goods is assumed to be positively related to
the expected real interest differential favouring the foreign country:
Substituting equations [14], [15] and [16] into [12] yields the following steady-state relationship:
where 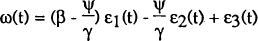
The long-run real exchange depends on the real interest differential, with an ambiguous sign, and on the stock of net foreign assets with a negative sign (a rise in net foreign assets causes the long-run real exchange rate to appreciate as net property income transfers from the rest of the world permanently increase). This equation forms the basis of the cointegration tests below. It differs from previous cointegration studies of the real exchange rate by explicitly allowing for the effects of financial liberalisation.
(c) Testing for Cointegration
The sample period chosen for testing the cointegration of the real exchange rate, the real interest differential and net foreign asset positions between the countries is 1974Q1 to 1990Q4 – wholly within the floating exchange rate era. Mussa (1986), for example, attributed a major role to the nominal exchange rate regime as a determinant of the behaviour of the real exchange rate. It is impossible to eliminate this exchange-rate regime influence entirely, though, since the French franc/Deutschemark rate within the EMS over the sample period is one of the currencies selected for study. The series used are defined as follows:
– the logarithm of the bilateral nominal exchange rate of currency A per unit of currency B, deflated by the CPI levels for countries A and B. The yen/dollar (yen/$), Deutschemark/dollar (DM/$), sterling/Deutschemark (£/DM) and French franc/Deutschemark (FF/DM) rates are considered;
– the long-term real interest rate of country A minus that of country B, the series which has had most success in obtaining significant and correctly signed estimates in other studies[5]; and
– the cumulated total current account surplus as a share of GDP for country A minus that of country B.
Tests for unit roots of the data were conducted first using the augmented Dickey-Fuller procedure with four lagged differences. The null hypothesis that the variable under investigation has a unit root is tested against the alternative that it does not. The results reported in Table 1 indicate that the null hypothesis is only rejected for the FF/DM real exchange rate. Subsequently, first differences of the remaining variables were also tested. The results (not shown) suggest rejection of the null hypothesis in each case. These results are consistent with the hypothesis that each series – with the exception of the FF/DM rate – is an integrated process of order one, I(1). If the globalisation of financial markets is the common factor explaining the non-stationarity of these variables, for the reasons outlined above, then it is important to include all three in any test for cointegration.
Tests for cointegration between the real exchange rate, real interest differential and cumulated current account difference are conducted using the methodology proposed by Johansen (1988) and Johansen and Juselius (1990). For the Johansen procedure there are two test statistics for the number of cointegrating vectors, i.e., the maximum eigenvalue and trace tests. For the maximum eigenvalue test the null hypothesis of zero cointegrating vectors, r=0, is tested against the alternative that r=1; r=1 against the alternative that r=2; and r=2 against the alternative that r=3. For the trace test, the null hypothesis is that the number of cointegrating vectors is less than or equal to r, where r is 0, 1 or 2. This is tested against the more general alternative. Critical values are reported in Johansen and Juselius (1990).
The results for these tests are presented in Table 2. For the maximum eigenvalue tests the hypothesis r=0 is rejected for the yen/$, £/DM and FF/DM real exchange rates (but not for the DM/$ rate). For the yen/$ rate the hypothesis r=1 is also rejected in favour of r=2, suggesting the presence of a second cointegrating vector. This was not the case for the £/DM and FF/DM rates, where the test of r=1 versus r=2 fails to reject the null hypothesis, suggesting one cointegrating vector in each case. These results are also borne out by the trace test. Thus r=0 is rejected for the yen/$, £/DM and FF/DM rates, while r≤1 is also rejected for the yen/$ rate.
In contrast to other studies then, three of the four real exchange rates considered are cointegrated with real interest rate and cumulated current account differences (yen/$, FF/DM, £/DM rates) over the floating rate period 1974Q1 to 1990Q4. The corresponding estimated cointegrating vectors are shown in the two right-hand columns of Table 2. In all cases, the vectors are of the correct sign, i.e. an improvement in the cumulated current account surplus favouring currency A is associated with an appreciation vis-a-vis currency B. In the cases where cointegration is found, a shift in the real interest differential favouring the foreign country causes the real exchange rate to depreciate.
The residuals from the cointegrating relationship are plotted in Chart 1 for the yen/$, FF/DM and £/DM real exchange rates. It is interesting to note that for the yen/$ and £/DM rates there are periodically substantial unexplained residuals over the floating rate era. A casual inspection of the charts suggests that the amplitude and periodicity of these swings – which presumably reflect inefficient expectational episodes – is similar in the 1980s compared to the 1970s, in spite of any liberalisation and globalisation of international financial markets. In the case of the FF/DM rate, on the other hand, there appears to have been a marked reduction in the amplitude of the residuals during the 1980s. From 1983, these lie within a range of 2 per cent on either side of the equilibrium rate, compared to about 10 per cent for the other currencies. This corresponds with France's decision in 1983 to favour the hard currency option within the EMS and the gradual establishment of credibility for this policy, reflected in the reduced frequency of realignments in the second half of the 1980s.
Two points are worth noting about the unexplained residuals. First, while they can be large and persistent (up to two years), they are, nevertheless, mean-reverting. Second, the trend towards globalisation and liberalisation of financial markets does not appear to have influenced the extent of these unexplained movements. That the amplitude of the residuals declined noticeably in the case of the FF/DM rate only, suggests that the exchange rate regime may be more important than the degree of financial liberalisation in explaining the extent to which inefficient expectation cycles influence nominal exchange rates. This latter finding is consistent with the view that a credible target zone for the nominal exchange rate exerts a stabilising influence on real exchange rate movements (as claimed in Krugman, 1988).
The above results suggest that it is necessary to account for both real interest differentials and cumulated current account imbalances when analysing the longer-run behaviour of real exchange rates. Moreover, the apparent non-stationarity of all three variables individually and their cointegration as a system for some major currencies is consistent with predictions arising from the increased globalisation of financial markets.
While the econometric results are consistent with the financial liberalisation interpretation given above, this nevertheless rests on two important assumptions:
- that globalisation has indeed increased over the sample period, reducing liquidity constraints by allowing the free flow of capital between countries which, in turn, should be associated with some reduction in national saving and investment correlations; but
- that globalisation of financial markets has not led to the integration of goods markets and a tendency for real interest rate disparities to be eliminated.
These issues are examined in the following section.
Footnotes
This is not the same as the nominal value of R*. Fixed interest debt is acquired over time at different interest rates and maturities. The concept here is an average rate. [2]
A similar specification is used in Frenkel and Mussa (1985), (p. 729). [3]
See, for example, Shafer and Loopesko (1983), Sachs (1985), Isard (1988), Meese (1990), Coughlin and Koedijk (1990), and Canarella et al (1990) who require a time varying parameter technique to find any relationship. [4]
See, for example, Shafer and Loopesko (1983), Sachs (1985) and Isard (1988). One reason often advanced for this is that real exchange rates take time to revert towards equilibrium, so that choice of a similarly long-term interest rate (which is the average of expected future short rates) is appropriate. The ten-year bond rate is employed, with inflation expectations being proxied by a centred three-year moving average. This is also used in Danker and Hooper (1989). Ten-year inflation expectations are unlikely to have much meaning in practice – witness that most official and model-based forecasts of inflation have an eighteen-month to two-year horizon. Attempts to generate ten-year forecasts of inflation with econometric techniques have never found support in empirical work on real exchange rates, e.g. Shafer and Loopesko (1983). The quarterly formulation assumes the rational forward-looking component has an eighteen month horizon. The long-run forecast is an average of this and the previous eighteen months of inflation experience. [5]