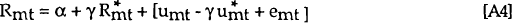RDP 9203: Real Exchange Rates and the Globalisation of Financial Markets Annex: Real Interest Parity

The linkage between bilateral ex ante real rates is examined using the following equation:

where E(R_mt) and 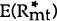are the ex ante or expected domestic and foreign real interest rates.

The hypothesis that foreign and domestic ex ante real rates move together and thus that the domestic and foreign markets are completely integrated implies γ=1. γ=0 implies complete disintegration. γ=1 and α=0 implies equality of domestic and foreign rates. The major practical problem here is that ex ante real interest rates are not directly observable. Cumby and Mishkin (1986) suggest an econometric methodology to tackle this problem. The ex post or realised real interest rate is:

where R_mt and i_mt are the realised real and nominal returns on the m period bond held from t to t+m and π_mt is the realised inflation rate from t to t+m. The ex ante real rate is defined as:

Combining the definitions of the ex ante and ex post rates gives:

Substituting for the ex post real rates (defined in equation [A3] to get rid of the unobservable ex ante rates in equation [A1] yields:

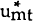is correlated with 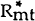because 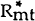is not realised until t+m and is thus obviously correlated with inflation forecast errors occurring in the interim between t and t+m. The composite error term is thus also correlated with R_mt. The use of an instrumental variable set (X_t) that is a subset of the information set available at time t will yield consistent parameter estimates since such instruments are, by definition, independent of subsequently realised forecast errors. In the present context, consistency also requires that the chosen instruments be uncorrelated with the error term in equation [A1].

With the current problem of overlapping data, however, an instrument set with the above characteristics will not result in consistent estimates of parameter standard errors. The Cumby, Huizinga and Obstfeld (1983) estimation procedure tackles this problem. Not only does it provide consistent estimates of the covariance matrix of the parameter estimates when the error term is serially correlated or conditionally heteroskedastic, but also produces more efficient estimates than the McCallum (1976) procedure.

Following Cumby and Mishkin (1986), a constant term, a time trend, the current nominal interest rate, i_mt, three lagged values of inflation are seen as suitable candidates for X_t. Unlike Cumby and Mishkin, however, we also find that one-period lagged values of money and output growth do add significantly to explanatory power for some countries. The sample residual autocorrelations from these regressions (not reported) are almost exactly the same as those reported by Cumby and Mishkin with no significant autocorrelations occurring at lags greater than 2, except at the seasonal frequency which may be spurious. This provides some indication that enough relevant information is included in X_t and that the fitted values which represent ex ante real rates will be reliable.