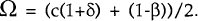RDP 9006: Wage Contracts, Sticky Prices and Exchange Rate Volatility: Evidence from Nine Industrial Countries 5. Results
November 1990
- Download the Paper 907KB
The first issue to be resolved was the choice of lag length, n, for the wage contracts. In practice, contracts of different lengths will exist in each country; the value of n that is chosen will be, by necessity an approximation. I employed the following Bayesian method for estimating n. Under the prior that n is equal to 2 or 4, equation (16) was estimated by non-linear least squares, yielding a freely estimated value for n. Next, depending on whether this point estimate was closer to 2 or 4, the hypothesis that n = 2 (or 4) was tested. This hypothesis was rejected in only one case, leading to an estimate of n = 2 (contracts of six months duration) for Australia and the United States, and n = 4 (contracts of one year's duration) for the other seven countries.[11],[12]
The estimated values of θ, c, β and θO (the optimal value of θ) are reported in Tables 1a and 1b. The estimates of θ show a low to moderate amount of indexation to inflation innovations, for all countries in the sample. (θ is estimated with the wrong sign for Australia and Austria, but is not significantly different from zero). For those countries where the point estimate of θ implies a moderate degree of indexation (France, Italy, the United Kingdom) the standard errors are small relative to this estimate.
| Australia | Austria | Canada | France | Germany | |
|---|---|---|---|---|---|
| θ | −0.095 (0.071) |
−0.076 (0.157) |
0.055 (0.050) |
0.229 (0.047) |
0.014 (0.036) |
| β | 0.117 (0.031) |
0.084 (0.020) |
0.088 (0.195) |
0.127 (0.050) |
0.187 (0.072) |
| c | 0.392 (0.047) |
0.495 (0.013) |
0.364 (0.080) |
0.459 (0.051) |
0.504 (0.231) |
| θO | 0.039 | 0.084 | 0.183 | 0.181 | −0.135 |
| SEEw | 1.431 | 1.585 | 0.287 | 0.396 | 0.300 |
| SEEwf | 0.611 | 0.238 | 0.535 | 0.341 | 0.630 |
| SEEp | 1.278 | 0.269 | 0.810 | 0.794 | 0.892 |
| SEEe | 6.225 | 1.725 | 1.766 | 2.793 | 3.634 |
| SEEpf | 0.379 | 0.653 | 0.406 | 0.484 | 0.376 |
| all SEE's ×100 | |||||
| Italy | Japan | United Kingdom | United States | |
|---|---|---|---|---|
| θ | 0.420 (0.049) |
0.041 (0.031) |
0.242 (0.009) |
0.122 (0.216) |
| β | 0.055 (0.065) |
0.081 (0.078) |
0.030 (0.030) |
0.036 (0.198) |
| c | 0.379 (0.139) |
0.454 (0.064) |
0.506 (0.039) |
0.501 (0.025) |
| θO | 0.636 | 0.478 | 0.010 | 0.194 |
| SEEw | 0.530 | 0.354 | 0.549 | 0.404 |
| SEEwf | 0.289 | 0.350 | 0.289 | 0.887 |
| SEEp | 0.897 | 0.543 | 0.179 | 0.363 |
| SEEe | 2.978 | 5.224 | 5.182 | 3.155 |
| SEEpf | 0.489 | 0.383 | 0.384 | 0.549 |
all SEE's ×100 |
||||
The estimates of θO range from a low of −0.135 for Germany to a high of 0.636 for Italy. In general, these estimates are quite low (the median estimate is 0.181), suggesting that the uncertainty created by nominal exchange rate volatility has led to a relatively high degree of uncertainty regarding the association between consumer and producer price inflation, relative to the variance of consumer price inflation innovations.
The hypothesis that θ is equal to its optimal value is tested with the results reported in Table 2. These show that the degree of wage indexation to inflation innovations significantly exceeded its optimal value in only two countries, the United Kingdom and Germany. For Canada, Italy and Japan, θ is significantly smaller than its optimal value. Table 2 also reports test of the overidentifying restrictions for the w,p and wf equations, and tests of the restriction θ + π = 1. The P-values suggest that the restrictions are consistent with the data.
| θ + π = 1 | θ = θO | Overindentifying | |||
|---|---|---|---|---|---|
| w | wf | P | |||
| Australia | 0.831 | 0.060 | 0.861 | 0.829 | 0.674 |
| Austria | 0.245 | 0.310 | 0.263 | 0.051 | 0.228 |
| Canada | 0.000 | 0.010 | 0.068 | 0.798 | 0.328 |
| France | 0.000 | 0.303 | 0.119 | 0.301 | 0.246 |
| Germany | 0.838 | 0.000 | 0.050 | 0.689 | 0.647 |
| Italy | 0.110 | 0.000 | 0.158 | 0.341 | 0.246 |
| Japan | 0.133 | 0.000 | 0.676 | 0.472 | 0.123 |
| United Kingdom | 0.000 | 0.000 | 0.202 | 0.072 | 0.426 |
| United States | 0.838 | 0.739 | 0.229 | 0.234 | 0.193 |
The numbers in the Table are P-values i.e. the minimum level of significance needed to reject the null hypothesis. |
|||||
The estimates of c and β show that every country exhibits a substantial degree of price and nominal wage rigidity. The countries with the most rigid prices are Germany, the United Kingdom and the United States, where c is estimated to be virtually at its theoretical upper bound. Prices in Australia, Canada and Italy are estimated to be relatively more flexible, but in each of these countries only about 25 per cent of the change in the equilibrium inflation rate (of producer prices) is reflected in the actual inflation rate in each quarter. The estimated value of c, for every country, is very well determined with the standard errors of the estimates being exceptionally small. The estimates of β, which are small and often insignificantly different from zero, indicate that nominal wage rigidity, at least in the short term, is substantial in all of the major industrial countries.
The conclusion to be drawn from Tables 1a and 1b appears to be very clear. The failure of PPP to hold is due to both price and nominal wage rigidities. Economists and policy makers who focus exclusively on one of these rigidities as a source of volatile real exchange rates are ignoring an important part of the explanation.
Of course, we should remember that the sample period for this study is relatively short, and that a longer time series might be more favourable to the market-clearing hypothesis.[13] Indeed, the model employed in this paper implies that PPP must hold true as a long run proposition, given the transversalilty condition on prices and the eventual convergence of domestic and foreign wages implicit in the error-correction mechanism (8c). Of course, the proposition that domestic and foreign prices will converge in the long run is of little practical use.
As mentioned above, the degree of wage indexation exceeded the optimum in Germany and the United Kingdom, ex post, leading to the conclusion that this factor was at least partially responsible for the considerable rise in unemployment in those two countries over the sample period. Why would unions have bargained for a degree of wage indexation which led to high unemployment? One possibility is that wages were set by union “insiders” who did not consider the effects of their actions on the “outsiders”; the latter bearing the unemployment consequences of the wage bargains (Lindbeck and Snower, 1988).
Another possibility, consistent with the evidence in this paper, is that the unions overestimated the optimal degree of wage indexation. This might happen, for instance, if the variance of nominal exchange rate innovations was underestimated. This misperception – even assuming rational expectations – by unions who negotiated wage contracts led to excessive wage indexation and hence the large rise in unemployment in those countries. This rise in unemployment reflects the welfare cost of nominal wage and price rigidities. Without these rigidities, PPP would be obtained, the variance of the innovations to nominal exchange rates would be small and costly misperceptions about changes in a country's optimal degree of wage indexation would not take place.
One of the major premises of this model is that the greater the degree of nominal wage and price rigidity the more unpredictable will be the nominal exchange rate. Denote the metric of these nominal rigidities by the sum
Ω lies between zero and unity, the lower bound being reached in the case of no wage or price rigidities, the upper bound being reached when prices and nominal wages are completely inflexible.
Table 3 presents two rankings for the nine countries in this study. The first is based on Ω, with the rank of 1 going to the country with the largest value of Ω, i.e. the greatest degree of nominal rigidities. The second ranking is based on unpredictability of the nominal exchange rate with the highest ranking going to the country with the largest SEE from its exchange rate equation.
| Ω | SEEe | |
|---|---|---|
| Australia | 8 | 1 |
| Austria | 3 | 9 |
| Canada | 9 | 8 |
| France | 6 | 7 |
| Germany | 5 | 4 |
| Italy | 7 | 6 |
| Japan | 4 | 2 |
| United Kingdom | 1 | 3 |
| United States | 2 | 5 |
|
The first column ranks countries in terms of nominal wage and price rigidities, with a rank of 1 referring to the greatest degree of rigidity, etc. The second column ranks countries in terms of nominal exchange rate unpredictability, with a rank of 1 going to the country with the largest variation of exchange rate innovations, etc. |
||
The correspondence between the rankings isn't perfect, but is very good nonetheless. Countries which have relatively flexible wages and prices also have relatively predictable nominal exchange rates, and vice versa. The two outliers in this test are Australia and Austria.[14] Australia has relatively flexible nominal prices and wages, but a relatively volatile nominal exchange rate; the converse is true for Austria. In both cases, we don't have to search far to find plausible explanations for these results. Australia's real exchange rate (and hence in the short-term, the nominal exchange rate) is in large part determined by changes in its terms of trade (Blundell-Wignall and Gregory, 1990). The sample period under consideration has seen considerable volatility in Australia's terms of trade, and the these effects have, in all likelihood, dominated the effects of nominal rigidities on the exchange rate.
The relative stability of Austria's nominal exchange rate is easy to explain, given the close ties between Austrian and German monetary policy and the large weight attached to Germany in Austria's trade weighted nominal exchange rate index (see the Appendix). The effects of nominal rigidities on Austria's exchange rate are outweighed by this effect. Significantly, Austria and Germany both exhibit a similar degree of nominal rigidities (they are ranked respectively, 3 and 5), but Germany's nominal exchange rate is more volatile than Austria's. This is also easy to explain. While changes in the value of the Deutschemark effectively dominate the value of Austrian Schilling, the converse is not true. Austria has only a relatively small weight in the DEM index.
Footnotes
n could not be estimated for Austria, so its wage contract length was made equal to that of its major trading and financial partner, Germany. [11]
The exception was Canada, where the estimated value of n was significantly greater than 4. However, for computational reasons, I used n = 4 for Canada. This decision was of no consequence since the estimate of θ turned out to be unaffected by the choice of n. [12]
Frankel and Meese (1987), in a study of the mean-reverting properties of the UK/US real exchange rate, are unable to reject PPP using a sample length of 116 years. [13]
Excluding these outliers, the relative rankings are never more than two places apart. [14]