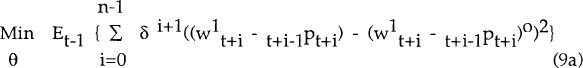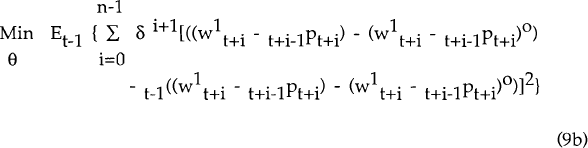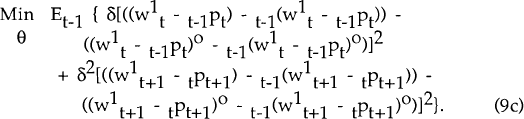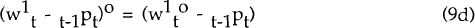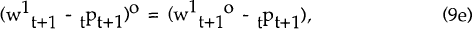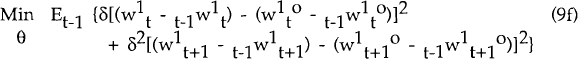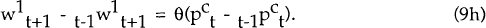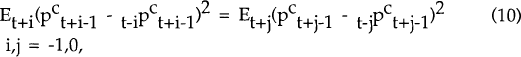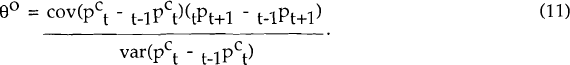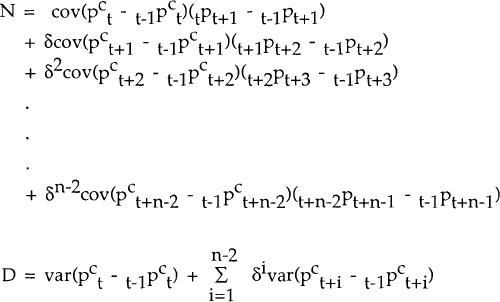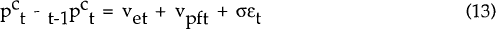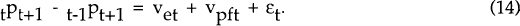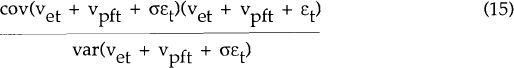RDP 9006: Wage Contracts, Sticky Prices and Exchange Rate Volatility: Evidence from Nine Industrial Countries 3. Optimal Wage Contracts

The optimal degree of wage indexation, θ^O, is the value of θ that makes the real product wage as close as possible to the labour market-clearing real product wage. A union which seeks to minimize unemployment for cohort 1 will thus have the following problem:

where 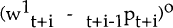is the market-clearing real wage for cohort 1 in period t+i. Since P_t+i. isn't observed until the end of period t+i, it is the expected value of this price level held in the previous period that is relevant to employment decisions in t+i.

As a practical matter, the problem (9a) cannot be solved because 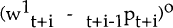is unobservable. However, suppose the problem is the following:

i.e. the union aims to minimize the discounted sum of squared innovations in the excess real wage. The minimand (9a) reduces to (9b) when 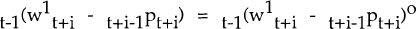i.e. when the expected real wage is equal to the expected market-clearing real wage in period t+i, for all i. Under the maintained hypothesis of optimal wage indexation, unions will rationally expect to set real wages to clear the labour market. In such a case, (9a) is equivalent to (9b) as a behavioural hypothesis.

The advantage of (9b) over (9a) is that it can be re-arranged into an expression with no unobservable terms. To see this, consider (without loss of generality) the simple case of n = 2. The problem is then:

Assuming that expectations of the aggregate price level are unaffected by cohort 1's wages,

the problem becomes:

From equation (1a)

From equation (1c)

The innovation in the market-clearing nominal wage for t+1, 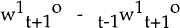is the sum of two parts. They are the surprise in the price level, _tP_t+1 − _t−1P_t+1 and the white noise shocks ξ_1t.

Cohort 2's problem is identical to cohort 1's, with the time subscripts moved forward one period. The union's optimization problem is to find the value of θ that minimizes the sum of the quadratic loss functions for the two cohorts. Assuming that consumer and producer prices are covariance stationary, so that e.g.

and that ξ_1t is uncorrelated with the innovation in the consumer price level, the problem is easily solved and the optimal value of θ is found:

In the general case of n-period contracts,

where

The empirical question of interest is to compare the estimated values of θ and θ^O, derived from equation (12). θ^O will tend to be small if the covariance between the j period innovation in the consumer price level in period t+j−1 and the revision, between periods t−1 and t+j−1, of the producer price level expected in period t+j+1 is small, or if the variances of the innovations to the consumer price level are large. Both will occur if the innovations to the nominal exchange rate have a large variance, which will occur, in turn, if the degree of nominal price and wage rigidities is large.

The model leaves open the possibility both nominal prices and wages are sticky (c ≠ 0, β ≠ 1) but the real product wage is not (θ ≤ θ^O). This apparent contradiction is reconciled by recalling that θ^O is the degree of wage indexation to consumer prices that minimizes the excess real product wage.

Suppose that following an adverse supply shock the real product wage is above its equilibrium level, and that nominal wages and prices are insufficiently flexible to restore this equilibrium. There are two alternative equilibrating mechanisms. The first is that the exchange rate appreciates, generating a fall in consumer prices and subsequently the nominal wage (via indexation) to restore the equilibrium real product wage. (Domestic prices will also fall, but not by as much as the fall in wages.) The second is that the exchange rate depreciates, leading to an increase in nominal wages. Domestic prices also increase, in this case by more than wages. Since the exchange rate, under both mechanisms, responds to unanticipated shocks, the underlying volatility in the exchange rate will be reinforced.^[8]

We should, however, recognize that these mechanisms provide the possibility, but do not guarantee, that the equilibrium real product wage will be attained. Since it is set exogenously, θ might still exceed θ^O. Recall that θ^O decreases when the variance of nominal exchange rate innovations increases. As nominal wages and prices become more rigid, this variance – which provides the essential link between real and nominal rigidities in this model – will increase and thus so will the likelihood that the actual degree of wage indexation exceeds its optimum.

If the value of θ estimated from the wage equation exceeds θ^O, then we can safely conclude that real wage rigidities are at least partially responsible for any observed rise in unemployment, either because wage setters have miscalculated θ^O or because they have deliberately chosen a value of θ in excess of θ^O. A more difficult issue is how the result θ ≤ θ^O should be interpreted. The most apparent explanation would be that, since under these circumstances wages are no more than optimally indexed to the price level, excessively high real wages cannot be a cause of unemployment.

However, this conclusion needs some qualification. The model assumes, but does not test, that the real wage that is set at the commencement of each contract for each cohort clears the labour market for that cohort. Obviously, this need not necessarily be the case. Suppose the economy is hit by a shock that necessitates a downward movement in the real wage. If this change does not take place a rise in unemployment will occur, which could be propagated beyond the length of all existing overlapping contracts even if wages are optimally indexed to prices thereafter.^[9]

It is also worth noting that since any of the covariances that form the numerator of (12) could be negative, the optimal degree of wage indexation could itself be negative. The intuition behind this seemingly curious result again stems from the assumption that wages are indexed to consumer prices but employment is a function of real product wages. Suppose that consumer prices are ex-post under-predicted and that, simultaneously, expectations of future producer prices are revised downwards, resulting in a negative covariance. The fall in expected producer prices implies an increase in the expected real product wage with consequent adverse effects on employment. These effects will be mitigated by a negative rate of wage indexation to consumer price innovations.

We should also note that even in the case of no nominal wage or price rigidities, the optimal degree of wage indexation will not be equal to unity, implying that the economy's aggregate supply curve will not be vertical. To see this, recall that in the market-clearing case

This implies that

and

The optimal degree of wage indexation, θ^O, is then given by

which, for non-zero ε, is equal to unity only in the closed-economy case of σ=l. The wedge between producer and consumer prices makes the aggregate supply curve non-vertical even in the case of competitive goods and factor markets.^[10]

Footnotes

The direction and size of the change in the exchange rate depends (implicitly) on the extent to which (or whether) the shock is accommodated by monetary policy. Fahrer (1989) examines this issue in detail. [8]

Optimal wage indexation can therefore be entirely consistent with the observation of high and increasing unemployment. However, the cause of the unemployment cannot be then ascribed to excessive wage indexation causing insufficient flexibility in the real wage. Rather, it is the cumulative effects of the initial shock (and perhaps subsequent shocks) which are responsible. [9]

The optimal wage indexation literature usually posits θ^O as a function of the variance of nominal and real shocks, the presence of the latter implying that θ^O is less than unity. The optimality condition (15) is entirely consistent with this result. In the presence of real shocks, ε ≠ 0, and θ^O < 1. If ε = 0, however, then θ^O = 1. [10]