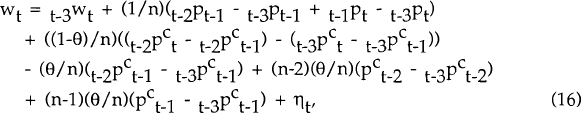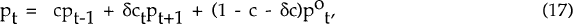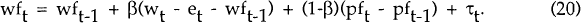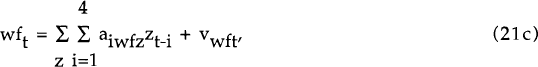RDP 9006: Wage Contracts, Sticky Prices and Exchange Rate Volatility: Evidence from Nine Industrial Countries 4. Estimation

The model to be estimated is:

Expressions for the expectations variables in terms of observable variables need to be derived before the model can be estimated. These are found by estimating the following quasi-VAR system.

where z = p,w,wf,pf,e

The parameters a_izz are estimated consistently and efficiently by Seemingly Unrelated Regressions. The estimates are of no intrinsic interest and so are not reported here; they are available on request from the author. The expectations terms are found by successive substitution into (21a) and (21b).

The expectations terms so derived are substituted into equations (16) and (17), with the parameters δ, σ and n imposed prior to estimation. The data are quarterly and the sample period is 1973(1) – 1988(4). I assume an annual real interest rate of five per cent and so δ, the discount rate, is equal to 0.98788. σ is the average share of imports in consumption over the sample period. Stationarity tests reveal that the variables p,w,wf,e and pf contain a unit root and so first differences of the data were taken prior to estimation. The use of stationary variables is particularly important with this model since the optimality conditions are derived underthe assumption of stationarity in the data.

Estimation of the model in first differences also serves two other useful purposes. First, it permits a test of the weak form of PPP, that percentage changes in the nominal exchange rate are equal to the difference between the domestic and foreign rates of price inflation. Tests of the strong form of PPP – that the exchange rate is equal to the ratio of the two price levels – are bedeviled by index number and other measurement problems that are largely avoided by testing the weak form. Second, dealing with inflation rates rather than price levels circumvents the use of the awkward non-stationary process u_t.

Three structural parameters are to be estimated: θ, the degree of wage indexation, and c and β, respectively the price and nominal wage rigidity parameters. Equations (16) – (20) are estimated by Hansen's (1982) Generalized Method of Moments, with allowance made for possible heteroscedasticity and serial correlation in the structural shocks η_t, ε_t and τ_t. The expected values of the endogenous variables (derived from the system (21a)–(21e)) are used as instruments.

Data definitions and sources are detailed in the Appendix.