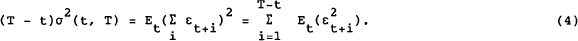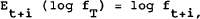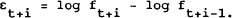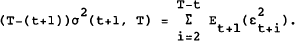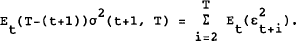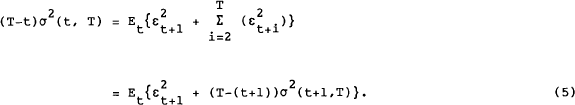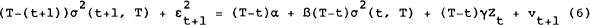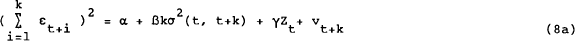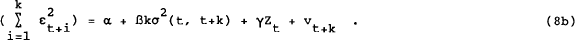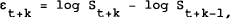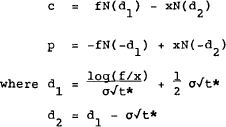RDP 8902: Option Prices and Implied Volatilities: An Empirical Analysis 2. A Test of Forecast Efficiency
May 1989
- Download the Paper 537KB
(a) Futures Options
The Black model for pricing options on futures contracts may be written in the following form:
| where | c is the price of a call option |
| p is the price of a put option | |
| f is the futures price at time t | |
| x is the option exercise price | |
| σ is the standard deviation of the futures price | |
| t* is the time to expiry.[1] |
The model assumes that both variances and interest rates are non-stochastic, and that the options cannot be exercised before expiry. Recent theoretical work by Ramaswamy and Sundaresan (1985), Schaeffer and Schwartz (1987) and Hull and White (1987) has begun to quantify the effects on option values when these assumptions are loosened; generally speaking the effects appear small when options are near the money or are relatively close to expiry. For example, the authors cited above compute pricing biases of the order of between zero and 1 per cent in Black-Scholes prices for at-the-money calls when the assumptions are violated. This may be compared with the size of discrepancies arising from likely errors in forecasting volatility. As an illustration, a 1 percentage point prediction error in estimating volatility on a one year option with true volatility of 0.1, would produce a mispricing of at-the-money calls of the order of 10 per cent under the Black-Scholes formula; such a prediction error would appear quite plausible when compared with observed historical variation in implied volatilities. These magnitudes, and casual observation, suggest that beliefs about volatility are likely to be much more important in determining actual option prices than beliefs about what is the appropriate pricing model, especially for options that are near the money. On this basis, we believe that an empirical focus on forecast accuracy rather than model accuracy is not unwarranted. It remains true, however, that the empirical results must be interpreted as being conditional on the assumption that Black-Scholes is a good approximation to the “true” formula.
All of the parameters of the Black model are readily observed in historical series apart from σ, which market participants are assumed to estimate. Given the option price, market estimates of σ can therefore be inferred by numerically solving equation (1) or (2). Cox and Rubinstein (1985) show that, provided conditional variances are non-stochastic, the implied values of σ2 taken at any time t can be interpreted as annualised conditional variances of the log expiry price. We can therefore write:
where the notation σ2(t, T) denotes the implied variance observed at t for an option expiring at T, expressed as an annual magnitude. Defining Et+i(log fT) − Et+i−1(log fT) Ξ εt+i, we have
The cross product terms in the above expression are eliminated by the rationality requirement that future revisions to forecasts are not correlated with current information at any point. Empirically, some measure of the innovation terms will be needed, and this paper uses the assumption that
which imlpies that
A theoretical justification for the above assumption is provided by Samuelson (1965), and strong empirical support is provided in an earlier study, Edey and Elliott (1988), which uses the same data set as the present paper.
By leading equation (4) one period, we also have
Taking expectations at time t:
This can be substituted into equation (4) to give
Equation (5) is a linear prediction equation relating current implied volatility to expected outcomes on observable variables realised in the next period. Standard efficient markets principles can be used to derive testable restrictions for this equation. In particular, if the current value of σ2 is an efficient predictor, then significant predictive power should not be added by the inclusion of further information dated t or earlier.
This suggests a test of forecast efficiency using an equation of the form
where Zt is a vector representing information observable at t. The additional
extraneous regressors are premultiplied by (T-t) to ensure that they always have the same order
of magnitude as the quantity being forecast. In the tests reported in section 4, Zt is taken to include current and past
values of 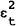 .
Under the null hypothesis, α = γ = 0, and β = 1.
.
Under the null hypothesis, α = γ = 0, and β = 1.
The interpretation of equation (6) is fairly straightforward. Under the efficient markets hypothesis, the current estimate of volatility remaining over the life of the option should be an optimal predictor of realised volatility, expressed as the appropriately weighted sum of next period's estimate and the realised squared price innovation in the next period. Although equation (6) is similar in spirit to equations tested by other researchers in this context, the exact linear predictive relationship used here has not to our knowledge been previously noted.
As an aside we note that a possible problem with the proposed test is that if the σ2 time series is nonstationary, the estimated β coefficient would be biased towards one, since the nonstationary magnitude appears on both sides of the regression equation. However the statistical results strongly suggest that the σ2 series are stationary.
(b) Currency Options
Although options on currency futures are traded on the Sydney Futures Exchange, the most active currency options market in Australia is in over-the-counter options, traded mainly in the interbank market. There is an important difference in the expiry date conventions as between the two markets. In futures options, only a small number of standard expiry dates are used (coinciding with futures expiry dates), so that a time series of data can be used to obtain a series of observations pertaining to the same expiry date. In over-the-counter options, the main indicator rates are for standard periods of time ahead of the trading date; thus a time series of data will show a series of options with equal time to expiry. In this case the algebra for deriving a testable equation is somewhat simplified because there is no need to “accumulate” variances in the way used above. The equivalent of equation (3) in this case is
leading to the regression equations
or
The difference between the two regression specifications is that the second imposes the zero restrictions on the expected value of the cross product terms, implied under the null hypothesis. This effectively removes one source of noise from the left hand side, and should result in improved efficiency in estimation. Equation (8b) is therefore used in the empirical work. To implement the equation, it is assumed that
where S is the spot exchange rate, thus assuming that the log of the spot exchange rate follows a random walk. Implied volatilities are obtained using the Garman-Kohlhagen (1983) version of the Black-Scholes model, developed for pricing currency options. Because the error terms in equations (8a and 8b) contain overlapping forecast errors, the method of Hansen and Hodrick (1980) is used to correct the estimated standard errors for the resulting serial correlation.