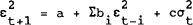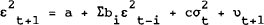RDP 8902: Option Prices and Implied Volatilities: An Empirical Analysis 4. Results
May 1989
- Download the Paper 537KB
The implied volatilities calculated from the data exhibit considerable variation through time, as can be seen in Figures 1 to 4. A minimal requirement for this behaviour to be consistent with rational forecasting is the existence of conditional heteroskedasticity in the time series for future prices. A useful means of testing for this in an atheoretical context is to specify a generalised ARCH process of the form:
where the ε's represent price innovations, and are observable. The equation is
atheoretical because it makes no attempt to match up the time horizon covered by the option
implied volatilities with the timing of subsequent innovations. Nevertheless the test is offered
as a preliminary indication of the information contained in option prices. If the b and c
coefficients are jointly zero, the prima facie conclusion would be that variances are constant,
and that any changes in implied volatilities would in reality be forecasting changes in variance
which do not subsequently occur. In fact the results, summarised in Table 1, provide fairly
robust evidence in favour of significant heteroskedasticity of the underlying prices, so that at
least this weak form of efficiency is not rejected by the data. Also, the implied volatilities
are usually significant. A reassuring aspect of this result is that the β coefficient in
the main regression equation (6), cannot then simply be interpreted as representing the ability
of  to
predict
to
predict  .
The implied volatility
.
The implied volatility 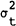 does contain at least some information
useful for forecasting the expected value of
does contain at least some information
useful for forecasting the expected value of 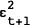 .
.
| Dependent Variable (Squared change in futures price) |
Constant | Implied σ2 |
Lagged Dependents | R2 | dw | |||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||||
| Bonds | .0002 (0.71) |
0.49 (1.97) |
0.13 (1.28) |
−0.06 (−0.57) |
0.38 (0.37) |
−0.13 (−1.31) |
0.20 |
2.00 |
| .0001 (0.61) |
0.32 (1.65) |
0.08 (0.75) |
(−0.04) (−0.36) |
0.10 (0.98) |
(−0.14) (−1.38) |
0.22 |
1.96 |
|
| Bills | .00 (−.08) |
1.49 (3.61) |
0.07 (0.75) |
−0.07 (−0.83) |
−0.04 (−0.37) |
0.17 (1.36) |
0.29 |
1.92 |
| .00 (1.39) |
1.37 (4.11) |
−0.05 (−0.60) |
−0.23 (−2.67) |
−0.03 (−0.35) |
−0.11 (−1.26) |
0.37 |
1.86 |
|
| SPI | .0004 (.23) |
0.896 (0.77) |
−0.35 (−2.91) |
−0.29 (−2.95) |
0.10 (1.02) |
0.13 (1.38) |
0.34 |
2.34 |
| −.002 (−0.89) |
3.34 (2.07) |
−0.57 (−3.58) |
−0.46 (−3.58) |
−0.07 (−0.66) |
−0.11 (−0.88) |
0.35 |
2.31 |
|
|
Notes: This table reports estimates of the equations
For each contract, the first row of results are estimated using call
volatilities, while the second uses puts. |
||||||||
The main sets of results involve direct testing of equations (6) and (8b), and are summarised in Tables 2, 3 and 4. The most striking feature of the results is that they consistently reject the efficient forecast hypothesis. For the interest rate and currency options, this rejection generally occurs through estimates of the β coefficients being significantly less than one. The interpretation of this is that changes in the estimated volatilities overpredict subsequent movements in the true variance of prices. With a typical β coefficient of around 0.7 for the interest rate options, the average extent of this overprediction is estimated to be about 40 per cent of the true changes in variance, or about 20 per cent when measured in terms of standard deviations. The apparent biases in currency options are even larger, with the β coefficient estimated at around 0.5 or less.
| Constant | β | Lagged squared innovations | Rho(4) | ||
|---|---|---|---|---|---|
| 4 | 8 | ||||
| Calls | 0.307 × 10−3 (2.69) |
.454 (8.61) |
−.261 (2.69) |
−.320 (4.19) |
−.023 |
| Puts | 0.278 × 10−3 (2.26) |
.337 (6.06) |
−.213 (2.11) |
−.261 (2.84) |
.035 |
Notes: The table reports estimates of equation (9b). Figures in parentheses are t-statistics. |
|||||
| Constant | β | Lagged squared innovations | R2 | dw | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||||
| Bonds | 0.5 × 10−4 (3.34) |
0.6989 (9.20) |
0.05 (1.33) |
0.03 (0.85) |
−0.05 (−1.50) |
0.04 (1.39) |
0.71 |
2.01 |
| 0.8 × 10−5 (0.66) |
1 |
0.02 (0.50) |
0.01 (0.21) |
−0.08 (−2.23) |
0.03 (0.86) |
0.66 |
2.18 |
|
| Bills | 0.5 × 10−6 (3.94) |
0.6224 (8.20) |
0.001 (0.06) |
0.003 (0.14) |
0.0005 (0.03) |
0.03 (1.19) |
0.72 |
1.91 |
| 0.1 × 10−6 (1.01) |
1 |
−0.009 (−0.40) |
−0.0008 (−0.04) |
−0.006 (−0.31) |
0.19 (0.63) |
0.66 |
2.15 |
|
| SPI | 0.6 × 10−3 (5.40) |
0.8048 (12.49) |
−0.17 (−23.03) |
−0.13 (−21.00) |
0.03 (5.01) |
0.04 (7.79) |
0.95 |
2.00 |
| 0.4 × 103 (4.38) | 1 | −0.19 (−29.46) |
−0.14 (−22.68) |
0.02 (3.92) |
0.03 (6.93) |
0.95 |
2.26 |
|
| Notes: The table reports estimates of equation (6) for call
options. Figures in parentheses are t-statistics. |
||||||||
| Constant | β | Lagged squared innovations | R2 | dw | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||||
| Bonds | 0.1 × 10−3 (3.96) |
0.5268 (5.68) |
0.05 (0.91) |
0.002 (0.03) |
−0.02 (−0.35) |
0.009 (0.18) |
0.61 |
2.17 |
| 0.2 × 10−4 (1.08) |
1 |
−0.05 (−0.88) |
−0.06 (−1.00) |
−0.08 (−1.34) |
0.007 (0.12) |
0.51 |
2.53 |
|
| Bills | 0.6 × 10−6 (4.87) |
0.7486 (8.84) |
−0.02 (−0.78) |
−0.04 (−2.21) |
−0.03 (−1.51) |
−0.01 (−0.58) |
0.61 |
1.85 |
| 0.4 × 10−6 (3.76) |
1 |
−0.03 (−1.79) |
−0.05 (−3.07) |
−0.04 (−2.12) |
−0.02 (−1.04) |
0.58 |
2.05 |
|
| SPI | 0.5 × 10−3 (4.76) |
0.9290 (12.30) |
−0.185 (−25.16) |
−0.17 (−29.32) |
0.03 (6.88) |
−0.001 (−0.25) |
0.97 |
1.91 |
| 0.4 × 10−3 (6.30) |
1 | −0.19 (−41.50) |
−0.17 (−38.18) |
0.03 (8.27) |
−0.004 (−1.33) |
0.97 |
1.99 |
|
Notes: The table reports estimates of equation (6) for put
options. |
||||||||
The above findings are fairly consistent across the interest rate and currency options data
sets, but somewhat different results are obtained for the SPI contracts, and it is important to
note that the SPI results are quite sensitive to the inclusion or exclusion of the sharemarket
crash. Results for the SPI options are therefore reported on both a pre-crash and a full sample
basis. It turns out that in both samples the joint null hypothesis is strongly rejected, but for
different reasons. Using the pre-crash sample, the β coefficient is estimated to be
substantially less than one (the point estimates are around 0.3) which, on the face of it,
suggests an even more significant element of market overreaction than appeared in the interest
rate contracts. The interpretation of this result is, however, clouded by the difficulty in
quantifying the effect of possible anticipations of a major market correction on the pricing of
options in the pre-crash period. Expected volatilities may have been influenced by such
anticipations, but there is no obvious way of testing for this because of the uniqueness of the
period around the crash. In the full sample, the results are quite different. The
estimated β coefficient comes out much closer to one, and in the case of put options is
insignificant from one. The joint hypothesis is nonetheless rejected in this case by the
significant negative coefficients obtained on elements of the distributed lag on 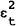 . This
feature is also observed in the currency options results. The negative sign here indicates that
. This
feature is also observed in the currency options results. The negative sign here indicates that
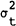 tends to
overpredict the subsequent variance when a large absolute price change has been recently
observed in the price of the underlying. This would be consistent with the view that market
volatility estimates are excessively influenced on average by current and recent measured
volatility in the price of the underlying. This result is equally true for puts and calls.
tends to
overpredict the subsequent variance when a large absolute price change has been recently
observed in the price of the underlying. This would be consistent with the view that market
volatility estimates are excessively influenced on average by current and recent measured
volatility in the price of the underlying. This result is equally true for puts and calls.
Once again, however, there are some difficulties of interpretation, because these results are dominated by the effects of the crash and its immediate aftermath. Following the crash, realised share price volatilities were actually slightly lower on average than they had been before it, yet the expected volatilities implied in both call and put prices remained historically very high (see Figure 3 where these volatilities are illustrated). Ex post, therefore, a forecasting rule which puts a negative weight on large recent absolute price movements is seen to produce estimates which are much closer to the true volatility. Given the unprecedented nature of this period, however, it seems likely that such a rule would take some time to be learned. Taken together, these considerations suggest that any conclusions concerning apparent biases in SPI options prices, need to be heavily qualified.