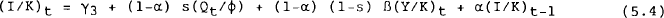RDP 8709: A Note on Aggregate Investment in Australia 5. Estimation

Before discussing the results, several comments should be made about the data.

(a) Data Assumptions

Equation (4.16) is estimated using quarterly Australian data for the period December 1966 to December 1986^[12]. As it stands, (4.16) is over-identified because we want to estimate α, s, β, and ϕ, yet we only have three variables on the right hand side. We therefore impose ϕ in the following analysis. One reason for this choice is based on data construction. The estimates of capital stock given in national statistics are based on the assumption of no cost of adjustment in investment and an accumulation equation which holds that every dollar of investment expenditure leads to an increment in the capital stock of one dollar.^[13] That is, I=J and therefore:

We have posited a theory that I≠J because of costs of adjustment and therefore must be careful to use this assumption when constructing the data for capital stock to test the theory. We take two approaches here. The first uses the available series for K^[14] and the second constructs a series for K using available data and an assumption about depreciation (δ) and adjustment costs (ϕ). In the second approach we incorporate equation (4.5) (which gives the relationship between the observed I and unobserved J) directly into the estimation of K, yielding a series for K which is based on the assumption that capital adjustment is costly. Here, each dollar of investment spending increases the capital stock by less than a dollar because of installation costs associated with it. The equation used for the generation of the K series is:

where J_t = investment expenditure less the adjustment cost of capital.

As J is not directly observable, it, like K, must be estimated. From (4.5) we see that a value for J_t can be inferred given knowledge of an initial value for K_t and I_t. We assume the value for J_t to be the positive root associated with the quadratic form of (4.5), given by:

Now K_t and I_t are known at t=0, but ϕ is not; hence, a series for J which evolves from (5.3) is dependent upon the value given to ϕ. A cost-adjusted K series can thus be generated for various levels of ϕ by using (5.2). In constructing the series for J and K, we assume a quarterly rate of depreciation on capital of 6 per cent per annum, and value capital stock in September 1966 at $56,032 million.^[15] We also choose a range of values for ϕ to test the sensitivity of results to this assumption. The values chosen are ϕ = 10, 20 and 30. These translate into a cost of 11 per cent, 21 per cent and 31 per cent of investment expenditure, respectively. The q series used are the updated estimates for Tobin's q in Australia produced by Dews (1986).

(b) Results

Having generated a series for J and hence K for different values of ϕ, we then use non-linear least squares to estimate (4.16), rewritten for convenience as:

Table 1 contains the estimation results for the standard capital stock series and the reconstructed series assuming ϕ=10, 20 and 30.^[16] The results for the standard capital stock data are shown in the first column. In this case, s, which is the share of investment based on q, is insignificantly different from zero. The coefficient β is significant but has no direct economic interpretation. The coefficient α, the speed of adjustment of actual to desired investment, is also significant. An a equal to 0.75 can be interpreted as an average lag of three quarters between the decision to investment and the appearance of half of the new productive capital.

Results for ϕ= 10, 20, and 30 are presented in the remainder of the table. The interesting feature of these results is the effect on the share of investment determined by q (the s coefficient), as ϕ is increased. In the case of ϕ=10, this coefficient is insignificant, but for ϕ =20 and 30, the coefficient is significant. We find that for any value of ϕ ≥ 16, the coefficient on q is significant. Note also that as ϕ is increased, both the significance and size of the s coefficient increases. Our priors are that the appropriate value of ϕ is at least 20, although this cannot be tested in the current model. This implies that as a lower bound, at least 10 per cent of investment is based on q while the remaining 90 per cent of investment is based on current profits.

Figure 1 plots the actual and predicted values of investment for the 1980s from the regression in the case where ϕ = 20. It can be seen that there appears to be no systematic tendency for the model to over or under predict the behaviour of investment.

In summary, we find that the model tracks investment expenditure quite well and that at least 10 per cent of investment is based on q theory while almost 90 per cent is based on current profitability.

Footnotes

The sources for (I) gross business fixed investment expenditure (non-dwelling construction plus plant and equipment) and (Y) gross domestic product – [constant 1979–80 prices/seasonally-unadjusted] – were ABS Cat#5206.0, Quarterly Estimates of National Income and Expenditure, Australia, March quarter, 1987 and ABS Cat#5207.0, Historical Series of Estimates of National Income and Expenditure, Australia, September quarter, 1959 to March quarter, 1980. [12]

ABS Cat#5221.0, Australian National Accounts, Estimates of Capital Stock 1985–86. [13]

Quarterly estimates of capital stock based on the annual estimates given in ABS Cat#5221.0 (constant 1979–80 prices). [14]

Constant 1979–80 prices. [15]

We experimented with ϕ from 5 to 30 and found results approximately proportional to those presented in Table 1. Note that seasonal dummies were included in the estimation, but results were not reported in the interest of brevity. [16]