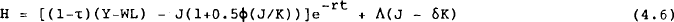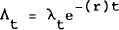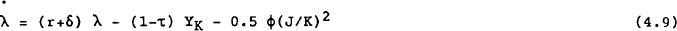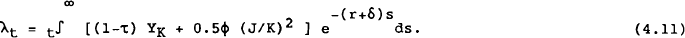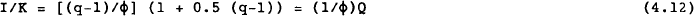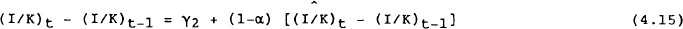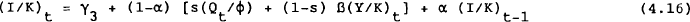RDP 8709: A Note on Aggregate Investment in Australia 4. Cost of Adjustment Model
October 1987
- Download the Paper 431KB
The cost of adjustment model which is used here to explicitly derive a q theory, is similar to that used in Hayashi (1982). We assume that price-taking firms choose factors of production to maximise the value of the firm subject to the constraint that capital is costly to adjust. The value of the firm is defined as the present discounted value of the stream of future after tax net income:
where
and
| τ | = effective corporate tax rate |
| πs | = real profits in period s |
 |
= relative price of investment goods which we assume equal to unity in period s |
| Is | = gross investment expenditure at period s |
| r | = real interest rate |
| Ys | = aggregate production in period s |
| Ws | = real wage in period s |
| Ks | = beginning-of-period stock of capital |
| Ls | = labour input |
Note that investment expenditure is defined outside the definition of real profits.
The firm is assumed to maximise (4.1) subject to an accumulation equation for the capital stock
Where
| J | = gross capital accumulation in period t |
| δ | = (constant) rate of depreciation on capital in period t |
and an equation which posits that capital is costly to adjust
where
ϕ = cost of adjustment parameter
0.5ϕ(J2K) = cost of installing an additional unit of capital t
Equations (4.4) and (4.5) assume that gross investment expenditure (I) increments the capital stock by gross capital accumulation (J), where the difference is the cost of converting goods into capital stock. This cost is assumed to be quadratic in the level of gross capital accumulation.
To assist in understanding the cost of adjustment model, equation (4.5) can be rewritten:
This clearly shows that the difference between gross capital expenditure (I) and gross capital formation (J), expressed as a proportion of J (that is, the cost of adjustment in terms of J) is a linear function of the level of J scaled by the existing capital stock. For example if ϕ=10 and I/K=.03, then from (4.5) we find J/K=.026. This implies the cost of adjustment is 13 per cent of J or 11.3 per cent of I. In other words, every $1 of I yields 88.7 cents of physical capital.
To solve this intertemporal optimisation problem we first define the Hamiltonian:
Define
Using the conditions for an optimum (∂H/∂L = 0; ∂H/∂J = 0; ∂H/∂K = −∂Λ/∂t) we find:
Equation (4.7) is a familiar result which states that an optimising firm will employ labour up to the point where the real wage (w) is equal to the marginal product of labour (YL).
Equation (4.8) can be written as:
Clearly, gross capital formation (J) is positive if λ>1 and negative if λ<1.
The evolution of the shadow price is given in equation (4.9). Note that (4.9) can be integrated forward and solved as:
Equation (4.11) gives the shadow value of investment as the marginal increment to firms' value arising from a unit increase in gross capital formation. The shadow price (λ) corresponds closely to the concept of Tobin's q. From this point, we assume λ=q.
Equation (4.10) can be used with (4.5) to find gross investment expenditure which is the observable variable:
where, for convenience, we assume Q = (q−1)(1+0.5(q−1)).
To estimate the model of aggregate investment we assume that s of investment in the economy is determined according to (4.12) and (1−s) of investment is undertaken by firms that are constrained by the amount they can borrow and lend and therefore invest out of retained earnings. These we proxy by assuming profits are a linear function of output. Specifically:
We use a superscript q to indicate optimising firms and n to indicate non-optimising firms. Aggregate desired investment expenditure is:
Here, optimising firms have total investment expenditure of Iq whereas non-optimising firms have total investment of In.
Further, we assume that investment decisions take time to come on line as investment expenditure, independently of the cost of adjustment. We posit a Koyck lag:
Substituting (4.12), (4.13) and (4.14) into (4.15) we find:
where γ3 = γ1 + γ2
Equation (4.16) is the equation to be estimated below.