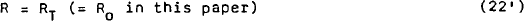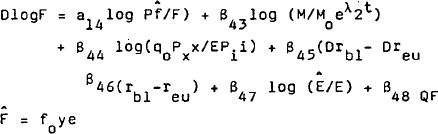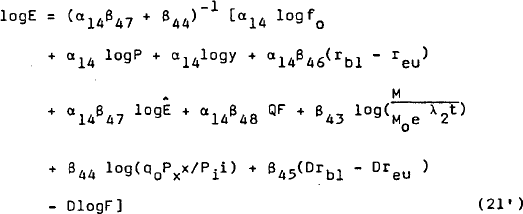RDP 8403: Modelling Recent Developments in Australian Asset Markets: Some Preliminary Results 4. The Foreign Exchange Market

The third change to be considered here is the floating of the Australian dollar in December 1983. This is modelled within the RBII framework as follows.

The authorities are assumed to decide on a target level for reserves, R_T, which reflects their intended intervention in each period; in the pure float modelled in this paper, this target level is constant.^[9] The supply of and demand for foreign exchange by private agents are then equated by movements in the exchange rate. Net transactions are, therefore, zero, so that the level of foreign reserves is unchanged at the (constant) target value.

The foreign exchange market is assumed to clear instantaneously since both demand and supply are elastic even within the trading day. This differs from the assumption about adjustment in the bond market, and requires that the specification of the net supply of foreign exchange is short-run in nature, and not a long-run “equilibrium” relationship as used elsewhere in RBII.

Mechanically, the procedure adopted involves alterations to three equations. The exchange rate reaction function is dropped from the model. The reserves equation is replaced with an expression which equates reserves to their target level:

The identity which is used in the estimated model to determine reserves is inverted to determine the rate of net capital inflow required to yield the change in reserves given by (22'):

Finally the estimated net capital equation

is inverted to obtain an equation for the floating exchange rate:

whe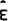re = E₀ (P/P_w) as before.

Since β₄₃, β₄₄ and β₄₇ are negative, while β₄₅ and β₄₆ are positive, it can be seen that the exchange rate responds positively (depreciates) to rises in the purchasing power parity rate Ê, world interest rates, and domestic money growth; and negatively (appreciates) to increases in domestic interest rates or surpluses on the current account (which necessarily correspond to negative values of DlogF).

To represent the removal of capital controls at the time of floating, the adjustment speed of net capital flows is increased. Moreover, the more rapid response of the exchange rate under floating suggests that expectations about the exchange rate should also adjust more quickly; the coefficient of logÊ in the demand for net foreign capital is therefore increased as well.^[10] Because of the short-run nature of the demand for net foreign capital implicit in equation (21'), no adjustment is made to the interest elasticities in this case.

It should be emphasised that, because the model is simulated as a simultaneous system, the exchange rate is determined jointly with capital flows and trade components even though it is the estimated capital flow equation which is used to calculate E.

The net supply of foreign exchange is the sum of balances on the current account and capital account. In RBII, these two components are proximately determined by different factors: the current account by activity and relative prices, with relatively slow adjustment speeds; and the capital account by expected relative rates of return and monetary conditions, with relatively fast adjustment speeds. (The capital account includes a small offset to the current account, due to the role of capital transactions in trade financing.) Under a pure floating exchange rate, where the net supply of foreign exchange is zero, the two markets are interdependent: a current account deficit or surplus must be offset by a capital account surplus or deficit of equal magnitude. The adjustment to any disturbance will take place through movements in the determinants of both the current and capital accounts.

Footnotes

The target level of reserves is set to the actual level at the start of the simulation period used. [9]

These modifications were used by Jonson, McKibbin and Trevor in their more-flexible-rate model. As already noted in Section 3 above, they were chosen to represent “sensible” responses to the change in exchange rate regime. In the present paper, the expectations parameter β₄₇ is reset from −0.5 to −5.0, while the adjustment speed is raised from 0.056 to 6.0. [10]