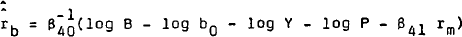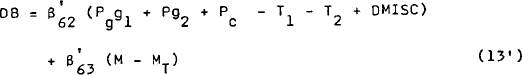RDP 8403: Modelling Recent Developments in Australian Asset Markets: Some Preliminary Results 3. The Bond Market

With the adoption of the tender system for selling government securities after 1982, the authorities no longer directly control the rates of interest on these securities. A quantity of paper to be offered for sale is now decided by the authorities, and the price is that at which the market will absorb this addition to the stock.

The method adopted for modelling this system is as follows. The estimated demand function for bonds is

This function is inverted to obtain the interest rate which would clear the market, which is denoted 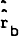. It is further assumed that the expected future bond rate, 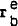, is equal to this market-clearing value. This yields an expression for 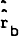as:

The actual level of the bond rate, r_b, is assumed to adjust towards 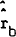through a first-order error-correction process as assumed in most RBII equations. Therefore,

This specification implies that the market will remain off its demand function for a time after any change in bonds. This seems reasonable given that the supply of bonds (through periodic tenders) is changed at discrete intervals and, therefore, that a “long-run” demand function such as that implicit in equation (20) will not move exactly in line with discrete jumps in supply.^[6] (It is the face value of bonds, not market value, that is modelled in RBII.)

Equation (20) is used to replace the reaction function for the bond rate in the estimated version of RBII. A new reaction function is assumed for the quantity of bonds supplied by the authorities:

This equation assumes that the supply of bonds responds partly to the size of the government's deficit and partly to the degree of monetary tightness desired. The two coefficients can be adjusted to provide for greater or lesser “weights” on the two objectives in the assumed policy reaction function.^[7]

It is also assumed that the interest elasticities of other asset demands will be altered by the change in structure in the bond market. Since the effect of the respecification of the bond and money markets will be to make interest rates more variable in the short-run, and as noted above the asset demands are long-run in nature, the interest elasticities of money demand and desired bank advances are reduced.^[8]

Following the reasoning of Jonson, McKibbin and Trevor (1982), this change may represent a “sensible” (though not necessarily “rational” in the Lucas sense) response of private sector demands to the structural change in the bond market.

Finally, it should be emphasised that equation (13') is only one simple member of a large class of possible reaction functions. For example, if the authorities were assumed to intervene in exchange markets, it would be necessary to introduce targets for international reserves as well as money, since any monetary objective could in principle be met by a mix of exchange market and bond market operations.

Footnotes

The interpretation of these demand functions as “long-run”, “equilibrium”, or “target” relationships is discussed in Davidson (1984), section 2, as well as in earlier papers on the RBII model. [6]

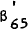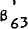In the simulations reported below, and are both set to 0.7. The use of alternative values for each, in a range of 0.4 to 0.8, has little effect on the qualitative results obtained. [7]

All interest rate coefficients in these functions are exactly halved, preserving homogeneity. The case of the demand for net foreign capital is treated below. [8]