RDP 1977-05: Modelling Monetary Disequilibrium 3. The Effect of Dropping the Monetary Disequilibrium Variable
September 1977
Because the role of monetary disequilibrium is relatively new in macroeconomic models, and as some of the channels discussed above for monetary disequilibrium are perhaps more controversial than others, the performance of two more conventional models is considered in this section. As the expenditure effect is probably the most widely accepted, Model 2 allows only this one channel for monetary disequilibrium: that is, γ1 = 0, for i = 2, …, 7. The second alternative. Model 3, removes all direct channels of. influence for monetary disequilibrium. Consequently Model 3 has only indirect channels for monetary and budgetary policy to influence macroeconomic behaviour. These indirect channels include interest rates, government expenditure and tax rates. Estimates of parameters and test statistics for both models are given in Appendix B.[29] Table 3.1 provides a summary of the test statistics for several key variables for each model.
| VARIABLE, TEST STATISTICS | MODEL 1 | MODEL 2 | MODEL 3 |
|---|---|---|---|
| d – r2 | .1335 | .1603 | .1451 |
| – RMSPE1 (%) | .9 | .9 | .9 |
| – RMSPE2 (%) | 2.6 | 2.7 | 2.2 |
| y – r2 | .2614 | .2505 | .2381 |
| – RMSPE1 (%) | 2.1 | 2.1 | 2.1 |
| – RMSPE2 (%) | 2.8 | 2.9 | 2.5 |
| P – r2 | .4835 | .2637 | .2597 |
| – RMSPE1 (%) | 1.0 | 1.1 | 1.1 |
| – RMSPE2 (%) | 3.1 | 2.8 | 4.5 |
| R– r2 | .4416 | .3016 | .3270 |
| – RMSPE1 (%) | 5.6 | 5.7 | 5.5 |
| – RMSPE2 (%) | 19.6 | 33.4 | 36.5 |
| M– r2 | .6871 | .6971 | .7091 |
| – RMSPE1 (%) | .7 | .7 | .7 |
| – RMSPE2 (%) | 5.3 | 4.5 | 8.7 |
For changes in prices and international reserves the r2cvalues from model 1 are substantially higher than those for models 2 and 3 while for this same test statistic, expenditure, output and money perform similarly in all three models. Whilst there is little difference between the models in terms of one-period simulation performance, in terms of the root mean square error in the dynamic control solution model 1 is substantially better only for international reserves, while for prices and money, model 2 has the closest fit. This conclusion must be qualified because of the role of the direct world price effect in the price equation, which as noted above (footnote 1, p.10) can be introduced to improve the simulation performance of the model. If, for example, β13 is set equal to .12 rather than .1 as in the simulations above, then model 1 performs better for prices and money than model 2. This result illustrates that further work on price determination is required.
As well as comparing the relative ability of each model to explain the historical data, it is also interesting to examine their dynamic properties in response to exogenous shocks. Each model is therefore simulated with a sustained increase of approximately 10 per cent in real current government expenditure. The dynamic responses of the models can be summarized by the resulting changes in inflation, end in the growth of real product, international reserves and money, relative to the control solution values.
There are three simulation paths in each panel of figure 1. The continuous lines refer to the deviation of growth rates from the control solution of model 1. The effect of the increase in government spending on the monetary growth rate in model 1 is broadly similar to that in the mid-1977 version of the RBA76 model discussed in Jonson and Butlin (1977), although in that case the monetary growth rate was below the control solution values for a period. One reason for the different response in the current paper is that the version of the model used in the earlier study suppressed the demand effects in the equation for bank advances, and as a result the monetary responses were more damped. Another factor is the lower coefficient on monetary disequilibrium in the price equation, and the lower value of the main adjustment, parameter (α7) in this equation. As a result of these two differences, the adjustment of prices is slower in the current version of the model, and the growth of real product falls below the control solution value between 3 and 4 years after the impulse, rather than 2 years after as in the earlier version.
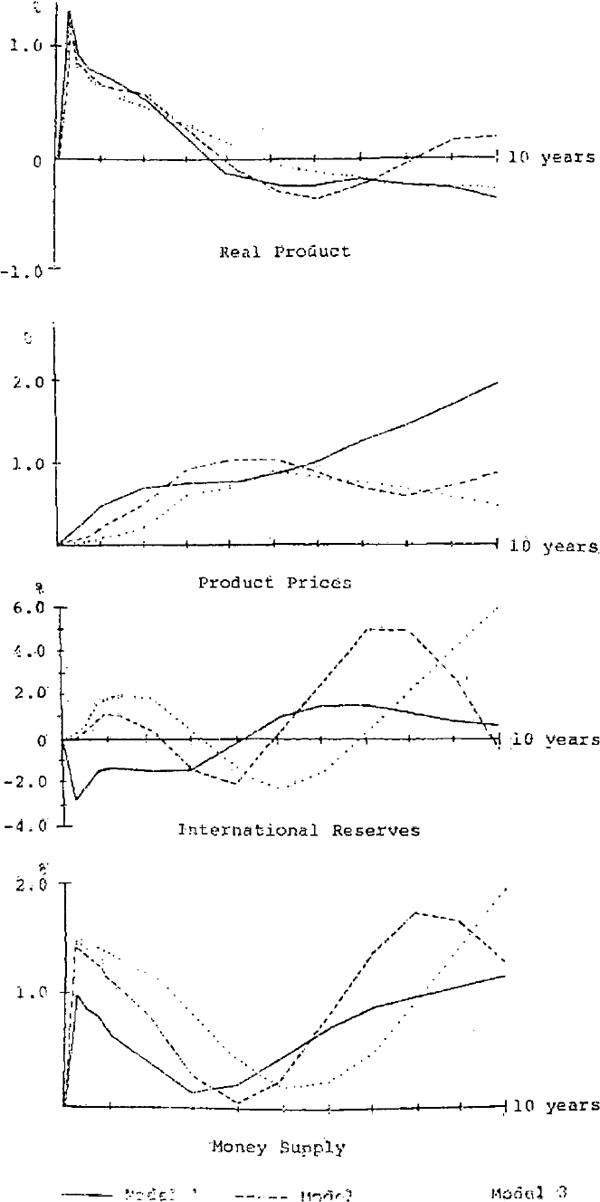
Another major difference between the current model and that of the mid-1977 version is the response of the balance of payments. In the current model the direct influence of flow disequilibrium in the money market leads to an immediate capital outflow, which is reversed later as the domestic interest rate rises.[30] In both cases, however, the sustained increase in real government spending produces a cyclical response in monetary growth. As the third panel suggests, this is largely as a result of the response of the balance of payments.
The initial decline in the growth of international reserves (relative to the control solution values) is largerly a function of increased imports and capital outflow. Imports grow more quickly than in the control solution because of relative price, and aggregate demand effects, and the fall in international reserves and higher monetary growth both contribute to a devaluation of the exchange rate and an increase in interest rates. The increase in interest rates produces an eventual increase in capital inflow, which is reinforced by the exchange rate expectation effects included in the model.[31]
After forty quarters the monetary growth rate is around one percentage point higher than in the control solution, and increasing gradually.
There are two features of the responses of models 2 and 3 which should be noted. Firstly, in both of these models, the balance of payments initially improves. Although imports increase by about the same amount as in model 1, there is a net capital inflow in models 2 and 3, induced by the increase in interest rates and devaluation of the exchange rate,[32] which is sufficient to more than offset the effect of increased imports.[33]
The second point is that the cyclical response of money and international reserves is more pronounced in models 2 and 3, with both models showing signs of unstable behaviour. It is difficult to specify in detail the causes of this monetary instability without a full dynamic analysis, but in general terms it may be noted that in model 1 the effects of monetary disequilibrium continue to operate until money supply equals money demand. Given that income, prices and interest rates, the determinants of money demand, all have a tendency to converge to equilibrium levels determined by the growth of world trade, world prices and world interest rates, this means that in model 1 money supply must have a tendency to converge on the values determined by money demand.[34] In model 2, with only one channel for monetary disequilibrium, this stabilizing tendency is weaker, and in model 3 it is absent.
In all three models the growth in real product is initially boosted in response to the increased real government spending, as illustrated in the first panel of figure 1. Thereafter the output responses differ somewhat, most markedly for model 2 in which the output cycle follows the monetary cycle – reflecting the real money balance effect on consumers expenditure – with peaks and troughs in product growth lagging two years behind those in monetary growth.
The behaviour of inflation is of particular interest because models 2 and 3, in which there are no direct monetary effects on prices, exhibit a weaker initial price response than model 1. The initial difference in the behaviour of inflation is not great, however, and this is because in model 1 the initial income effects on the demand for money tend to cancel the money supply effects, and it is only when income begins to decline that excess supply of money becomes important.[35] At the end of the simulation period, however, the differential inflation rate in model 1 is considerably greater than that in models 2 and 3,[36] although it is possible that the stronger output performance in model 2 could produce higher inflation at a later date.
Footnotes
In Model 2 it is necessary to constrain the bond rate elasticity in the demand function for money. In Model 3 none of the parameters in the demand function for money are identified, and omitted from the of the model. [29]
As compared with the relevant simulation path in figure 1 of Jonson and Butlin (1977), the initial reduction in the growth of international reserves is much sharper in the current model. [30]
Devaluation of the exchange rate produces a ceteris paribus expectation of later revaluation. [31]
When these simulations are repeated with a fixed exchange rate, the balance of payments offsets are considerably greater in all three models, although there is again a (short-lived) initial increase in international reserves in models 2 and 3. [32]
In models 2 and 3 the response of capital flows to interest rates and exchange rate changes is greater than in model 1, as indicated by a comparison of parameters β21 and β23 in equation 13 in each model. [33]
Unless there are strongly destabilizing feedbacks which work in the other direction. While, as noted above, there is some evidence of this in model 1, the tendency is far stronger in models 2 and 3. [34]
This effect is reinforced over time by the rising interest rates. [35]
And the exchange rate has devalued by more. [36]