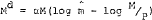RDP 1977-05: Modelling Monetary Disequilibrium 2. Monetary Disequilibrium and its Channels of Influence
September 1977
2.1 The Role of Monetary Disequilibrium
The effects of monetary variables on output and prices in closed economy models has received widespread support from large structural and small reduced form models of the American economy.[3] For smaller, more open economies, there is probably more controversy, in particular about the relative size of the reactions of the balance of payments and domestic variables over different time periods.[4] It is probably fair to say that many economists, especially those of the “monetarist” persuasion, regard the domestic monetary linkages in most large models as too weak, at least in the short run. Conversely, economists who adopt a structural approach are critical of two aspects of the “reduced form” approach of some monetarists. Firstly, from a methodological point of view, reduced form studies by definition fail to identify empirically the linkages in the transmission mechanism. Secondly, results from reduced form studies that incorporate the monetary approach to the balance of payments, and which suggest the existence of strong and fast offsets through changes in international reserves, often impose rapid adjustment of financial markets;[5] these results need to be tested in a general framework which allows the lags to be determined by the data.
Somewhat surprising in view of the controversy about the strength and direction of monetary effects in the short run, many economists seem to share a common vision of the transmission mechanism. This general view of the process of adjustment is stated succinctly by Friedman and Schwartz.
It is this interconnection of stocks and flows that stretches the effect of shocks out in time, produces a diffusion over different economic categories, and gives rise to cyclical reaction mechanisms. The stocks serve as buffers or shock-absorbers of initial changes in rates of flow by expanding or contracting from their ‘normal’ or ‘natural’ or ‘desired’ state, and then slowly alter other flows as holders try to regain that state.
In this stock-flow view, money is a stock in a portfolio of assets, like the stocks of financial assets, or houses, or buildings, or inventories, or people, or skills. It yields a flow of services as these other assets do; it is also subject to increase or decrease through inflows or outflows, as the other assets are.”[6]
As this extract makes clear, a whole vector of asset disequilibrium affects would be expected to influence adjustment of consumption, asset accumulation, and perhaps prices and factor demands.[7] Yet some economists – notably Friedman and his followers – have insisted that money has a major role in economic dynamics. This may be because disturbances from the supply side of the money market are larger and more frequent than disturbances in other markets. In a world of considerable uncertainty and with sizeable monetary disturbances, it may be rational for money to be used as a buffer stock which is allowed to soak up the effects of the outcome of decisions in all other markets in the short run. This is not to imply that economic agents are indifferent about the amounts of money which they hold – indeed, according to this view they will use the gap between actual and desired money balances[8] to signal the need to adjust their decisions about household expenditures, prices, asset and factor demands.
The view of money[9] as a buffer stock and signalling device is adopted in the RBA76 model used in this paper, with the quantity of money determined residuaily in the short run.
2.2 The Money Supply Process
The buffer stock hypothesis implies that the private sector will accept, in the short run, large variations m its money holdings in order to achieve its consumption and non-monetary wealth targets. Thus, while it may be possible to identify directly a “short–run” demand function for money which is able to capture these variations, this function would be more complex than those for other assets, and so it seems appropriate to treat money as the residual asset in the model.[10] To achieve this, changes in the volume of money (DM) are specified as the sum of changes in international reserves (DR) and domestic credit expansion (DC), that is
DM = DR + DC
This identity (equation (8) in the model in Appendix A) also includes the government's budget identity as a determinant of domestic credit expansion.[11] This “sources” identity for the volume of money could have been complemented by a “uses” definition[12] in a more detailed model but the current model concentrates on identifying the components of the balance of payments [exports, imports, and capital flows) and the equations of the financial sector in broad terms (total bank advances of the private sector, net capital flows and non-bank holdings of government bonds are the financial variables in the model).
In the long run, the stock of money will converge to its desired level as monetary disequilibrium influences other asset choices, expenditure and prices. Its role in these adjustment processes will tend to remove any discrepancy between desired and actual holdings of money through induced changes in expenditure, prices and factor demands, changes which will influence in turn the balance of payments, domestic credit expansion and the stock of money.
2.3 The Demand for Money
Nearly all studies of the demand function for money are Carried out in a single equation framework. The two standard forms in this single equation work have assumed that the economy is always on the demand function for money, or that the quantity of money adjusts to demand with a first order stock adjustment process.[13]
Several recent Australian studies have tested these forms, with conflicting results.[14] One area where results have differed is on the degree of stability of the demand for money function. the usual way to overcome apparent instability is to make changes to the specification of the demand for money function, or of the dynamics of adjustment, and one common specification change is to include supply factors.
An alternative is to estimate the demand function for money implicitly, as part of a full model of the economy. This is the procedure followed in this paper; as noted above, it is based on the view that money is a buffer stock. By having money determined residually in the short run, the specification allows both supply and demand factors to influence actual money holdings. The fact that money, as an asset, has to converge to its desired level in the long run, and that disequilibrium money balances have various channels of influence in the model means that the parameters of the long-run demand function for money can be identified, even if the full system does not converge directly or the desired demand for money.
The clear advantage of this specification is that, if money is the residual asset in the short run then disturbances to the money supply will force economic agents away from the long-run demand function for money. The instability in money demand relationships estimated in the usual manner when there are large disturbances from the supply side of the money market suggests the need for an approach similar to the one in this paper. The specification in the RBA76 model is compared with a more conventional approach in Section 4.
2.4 Channels for the Influence of Monetary Disequilibrium
The most widely recognised channel for the effects of monetary disequilibrium is on aggregate expenditure. If, for example, a consumer suffers a temporary drop in income, then in order to maintain expenditure the consumer will divert a proportion of his buffer asset holdings so as to achieve his desired expenditure. However, a sustained disequilibrium in the consumer's holdings of his buffer asset will indicate that more than temporary influences are operating and that expenditure should be adjusted to be consistent with the new set of conditions.[15] Equation (1) in the model is for aggregate household expenditure.
Given that monetary disequilibrium is important for the expenditure decision of the private sector it would appear likely to also influence other private sector asset decisions such as the holdings of government securities and net foreign assets. Empirical work has not been able to identify an influence for monetary disequilibrium on the demand for bonds, but such an influence is identified in the equation explaining net capital inflow. As indicated by equation (7) of the model the nature of this influence is somewhat different to that in the expenditure equation.
In a recent paper, Jonson and Rankin (1977) examine five alternative treatments of the
monetary and balance of payments sectors in a model of the U.K. economy. In these
experiments capital flows are considered as either (i) a residual identity;
(ii) a portfolio decision modified by a measure of stock disequilibrium in the money
market; or (iii) a portfolio decision modified by a measure of flow disequilibrium in
the money market. Stock disequilibrium in the money market is measured in the usual way as
the gap between actual and desired real money balances, that is, 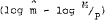 .
Flow disequilibrium in the money market is defined as the differences between the flow
demand for money Md) and domestic credit expansion (DC), that is,
(Md − DC) where the flow demand for money is defined as
.
Flow disequilibrium in the money market is defined as the differences between the flow
demand for money Md) and domestic credit expansion (DC), that is,
(Md − DC) where the flow demand for money is defined as
The results of similar tests for the Australian economy suggest that the specification in which flow disequilibrium in the money market influences capital flows is preferred to the other specifications, including those in which a measure of monetary disequilibrium influences the overall balance of payments.
Money in this model serves not only as the buffer stock for households but also for firms.[16] Consequently decisions made by firms may also be influenced by monetary disequilibrium.[17]
In the firm's pricing and production decisions, a very general approach has been taken. In each case there is a basic adjustment, to desired investment or labour demand in the case of equations 2 and 3, to costs or world prices in the case of equations 4 and 5 which represent pricing decisions,[18] and to aggregate demand in the case of output and imports. These basic adjustments are assumed to take place in an hierarchacal manner, with output and imports determined first, then factor demands and prices. The latter decisions are based in part on marginal productivity and the investment decision might be regarded as the most long-run in its orientation.
In each case, monetary and inventory disequilibrium terms have been included in addition to the basic adjustment mechanism, as possible influences on the disequilibrium dynamics. The results are mixed, and the model presented below contains only those channels about which the evidence is relatively unambiguous. Firstly, it has not been possible to obtain significant monetary disequilibrium effects on the adjustment of output or imports, and these are not considered further in this paper.[19] With respect to factor demands, it has been possible to identify a small but significant monetary disequilibrium effect on investment in sortie model runs, but this result is not robust and the relevant parameter is constrained to zero in the results reported below. In the case of labour demand, however, monetary disequilibrium seems to be quite important in the adjustment process.
In the price equations there is clear evidence for a significant effect of monetary disequilibrium in the determination of product prices, but the parameter on inventory disequilibrium is usually small and insignificant, and has been set to zero. Both monetary and inventory disequilibrium are sometimes of the wrong sign in the export price equation, and both of the relevant parameters have been set to aero in the current model. As in the model of the U.K. economy presented by Jonson (1976b), this result is consistent with the hypothesis that firms have little monopoly power in export markets.
In each of the equations representing firms’ decisions, the monetary disequilibrium variable can be interpreted as representing price or product expectations. Given the influence of excess money in the expenditure function, it could be rational to raise prices or factor demands in response to excess money balances, and it would not be surprising if the price expectations effect became relatively more important as inflation accelerated and the exchange rate became more flexible.
Equation (6) in Appendix A sets out the wage determination process in the model, with monetary disequilibrium again capturing the effects of price expectations. The main adjustment terra captures the fundamental productivity determinants of real wage movements while the ratios of labor demand to supply, and of real award wages to trend reflect additional demand pressure and expectational effects in the labour market.[20]
The seven equations denoted as Group 1 equations reflect the basic channels through which monetary disequilibrium is likely to directly influence economic behaviour. Group 1 also includes the equation determining changes in the volume of money.[21]
Group 2 equations, also set out in Appendix A, consist of those equations in which monetary disequilibrium does not seem to play a direct role, or identities. The behavioural equations are labour supply; exports; imports and output; price of government current goods and services; non-bank private sector demand for bonds; bank advances;[22] tax receipts; the bond rate; the exchange rate; and interest payments on government debt. The identities determine the business fixed capital stock, labour demand, changes in foreign reserves, domestic credit expansion, and changes in inventories of goods.
Table 2.1 sets out the estimates of parameters γ1 to γ7 which represent the influence of monetary disequilibrium in equations (1) to (7) of the general model, together with the t-ratios calculated from the parameter estimates and their asymptotic standard errors.[23] They are compared with the corresponding parameters from the late-1976 version of the RBA76 model[24] and the mid-1977 version of the model.[25] As can be seen from the parameter estimates in Appendix A, the additional channels for the effect of monetary disequilibrium (and other minor changes made to the model)[26] have not had a large influence on the parameters by comparison with the estimates in the earlier versions of the model.
| PARAMETER | MODEL | |||||
|---|---|---|---|---|---|---|
| MODEL 1 | LATE-1976 | RBA76 | MID-1977 | RBA76 | ||
| γ1 | −.2428 | (5.40) | −.2489 | (5.99) | −.2634 | (6.44) |
| γ2 | 0.0 | 0.0 | 0.0 | |||
| γ3 | −.0793 | (3.27) | 0.0 | 0.0 | ||
| γ4 | −.1213 | (4.59) | −.0982 | (3.51) | −.2262 | (6.80) |
| γ5 | 0.0 | 0.0 | 0.0 | |||
| γ6 | −.2363 | (6.27) | −.1713 | (4.06) | −.2068 | (5.32) |
| γ7 | .0619 | (3.30) | 0.0 | 0.0 | ||
Across models the estimates of γ1, γ4 and γ6 are reasonably consistent, with the exception of γ4 from the mid-1977 version of RBA76. These results are reassuring in that they indicate that there is no major trade-off between the different channels for the influence of monetary disequilibrium, although the lower value of γ4. in the current version of the model is somewhat puzzling since the results for the mid-1977 version in which γ4. approximately equalled γ6 suggested that excess money had no direct impact on real wages.[27] These results could also be taken to indicate that the specification errors implied by setting γ3 and y7 equal to zero in the earlier versions of the model did not cause major problems elsewhere in the system.
The parameters in the remainder of the model are similar to those in the mid-1977 version of the model. One set of parameters of particular interest are those of the long-run demand function for money, β1 and β3 to β6. These parameters are reported in Table 2.2, along with similar parameters from earlier versions of the model.[28]
| PARAMETER | MODEL | |||||
|---|---|---|---|---|---|---|
| MODEL 1 | LATE-1976 | RBA76 | MID-1977 | RBA76 | ||
| β1 | 1.0* | 1.0* | 1.0* | |||
| β3 | −.1608 | (4.11) | −.3010 | (3.41) | −.18 | |
| β4 | −.1037 | (4.54) | −.0959 | (2.87) | −.1441 | (4.67) |
| β5 | −.01* | −.0216 | (0.90) | −.01* | ||
| β6 | .1145 | (1.91) | .1555 | (2.38) | .0970 | (2.10) |
|
* Denotes value constrained |
||||||
Footnotes
The MPS Model, for example, includes wealth, interest rate and “availability” channels for the influence of changes in monetary policy. These channels are sufficient to ensure that the standard monetarist results are achieved “in the very long run” (Modigliani (1975, p. 241)). For an example of a much smaller model with strong monetarist features in the short run see Anderson and Carlson (1970). [3]
Some writers, notably Kouri and Porter (1974), assume that domestic price and output reactions to excess money are relatively unimportant and that excess money is removed by offsetting capital flows in a very short period; others, such as Helliwell and Lester (1976) who use the RDX2 model of the Canadian economy, report significant domestic effects of monetary disturbances, despite the existence of significant “offsets” through short term capital flows. [4]
In addition to the work of Kouri and Porter (1974) and Porter (1974), the empirical studies in Frenkel and Johnson (1976) are relevant. [5]
Friedman and Schwartz (1963, p.234). For similar views see Brainard and Tobin (1968, p.352) and Tobin (1971, p.487). [6]
For attempts to implement such a generalised view of the transmission mechanism for Australia, see Parkin et al (1973) and Purvis (1975). [7]
Where desired money balances are defined in the usual way as depending on income (or wealth) and a vector of interest rates. [8]
The precise definition of the asset called “money” is still controversial with possible definitions ranging from very narrow money aggregates such as base money, to broader financial aggregates such as M3, M5 or even financial aggregates that include government bonds. The precise definition of money is not at issue in this paper although the choice of what is “money” is important when specifying the demand and supply functions for money. This paper uses a definition of money as M3, future work will examine alternative definitions. [9]
This procedure, as discussed below, still allows the implicit estimation of a “long-run” demand function for money which is combination to the other assests input function of the system. [10]
For a discussion of this see Christ (1971). [11]
The “uses” definition of money would be the sum of notes and coin, demand deposits, time deposits and savings bank deposits if M3 was chosen as the definition of money. [12]
Those writers who have followed Feige (1967) have assumed a second order adjustment process. In these cases too the adjustment is directly influenced by demand for money. [13]
Recent Australian studies on the demand for money have been Adams and Porter (1976), Norman and Purvis (1975), Pagan (1977) and Sharpe and Volker (1977). An interesting discussion of the Adams and Porter paper and other issues related to estimating the demand for money can be found in Conference in Applied Economic Research: Papers and Proceedings, Reserve Bank of Australia, 1976. [14]
This behaviour is considered in more detail by Jonson (1976a) who uses the one good, one asset model of Archibald and Lipsey (1958) to demonstrate the role of a buffer asset in cushioning expenditure patterns from unexpected shocks to income. [15]
Firms are assumed to use inventories of goods as an additional buffer asset; see Jonson, Moses, and Wymer (1976). [16]
There are unresolved conceptual and empirical problems which have prevented an explicit disaggregation of the private sector into households and firms. One necessary assumption for the approach in the paper is that aggregate monetary disequilibrium is positively correlated with monetary disequilibrium of firms and households. [17]
There is also a term representing direct world price effects on product prices during the period of fixed exchange rates. This term is not introduced in the estimation of the model, but its inclusion in simulation corrects for a tendency to over-predict prices during the 1960's. Together with some evidence that the weight on the monetary disequilibrium term in the price equation has risen since the move to more flexible exchange rates, this result suggests that the way in which prices are set has changed in recent times. This is an area where considerable research is needed. [18]
There are strong indirect effects of monetary disequilibrium on output and imports, acting through expenditure. [19]
See Jonson, Moses and Wymer (1976) for a more detailed discussion of the price and wage equations in the RBA76 model. [20]
This equation is included in Group 1, as in Section 4 the manner in which changes in the volume of money are determined is altered from being the residual of all other decisions as reflected in the balance of payments and domestic credit expansion to being determined by a first order stock adjustment process. This alternative is denoted by equation (8a). When this second alternative is followed, the balance of payments equations have to be changed as discussed in Section 4. [21]
The supply of bank advances is assumed to depend directly on the quantity of money, which is a proxy for bank deposits, the major liability of the banking system. [22]
Appendix A contains a complete set of parameter estimates and test statistics for the current model – denoted Model 1. As noted above, γ2 and γ5 are set to zero in the current version of the model. [23]
The original version of RBA76 was estimated to 1974(4) and the results are reported in Jonson, Moses and Wymer (1976). [24]
This version was estimated to 1975(4) and the results are reported in Jonson and Taylor (1977). [25]
These changes include the introduction of an equation explaining the interest payment on government debt and a second order labor demand equation; simplified interest rate and exchange rate reaction functions; and interest rates are entered in linear form rather than log-linear form throughout the model. [26]
See Stein's discussion of Jonson and Taylor (1977) on this issue. [27]
In Table 2.2, the interest rate parameters are the mean elasticities, to facilitate comparison with the earlier results. As noted earlier, in the current model interest rates are measured in linear rather than in logarithmic form. [28]