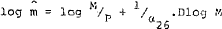RDP 1977-05: Modelling Monetary Disequilibrium 4. A model with a Conventional Demand Function for Money
September 1977
Models 1, 2 and 3 estimate the demand for money function implicitly, and changes in the volume of money are determined residually (as specified in equation (8) of the model). As discussed in section 2 a more familiar way to estimate the demand for money function and the changes in the volume of money together (usually in a single equation framework) is to assume a first order stock adjustment of the actual money stock to the desired demand for money. In this section, this alternative procedure is tested by estimating model 1 with equation (8a) rather than equation (8).
An equation of this form can be interpreted either as a structural equation for the demand for money, or as a “quasi reduced form equation” which summarises the full systems adjustment of the stock of money to the demand for money. This alternative specification introduces the parameters of the demand function for money into equation 8, as well as in the other equations which are assumed to be influenced by monetary disequilibrium. Some economists may be interested in the results of estimating the demand function for money in equation 8 alone, and so two models are estimated in this section. In the first (model 4), a single demand function for money is estimated; in the second (model 5) two sets of parameters are estimated, one set in equation 8 and the other in equations 1, 3, 4, 6 and 7.[37] The parameters from equation 8a in the second case are denoted β3*, β4*, β5* and β6* in the results reported in Appendix C.
To maintain consistency in the monetary sector the use. of equation (8a) implies that a variable other than money must become the residual item. Following several recent studies in the framework of the monetary approach to the balance of payments the residual is assumed to be foreign reserves which means that equation (18a) for the balance of payments is used in conjunction with equation (8a) for the changes in the stock of money.[38] In addition the specification of the capital inflow equation is altered so that the balance of payments identity is not over-determined. Consequently, equation (7) is replaced by equation (7a).
The models resulting from these changes could be regarded as structural versions of the reduced, form model estimated by Kauri and Porter (1974) in the sense that the money supply would equal money demand within a short period if the estimate of α26 was very large,[39] and capital flows would, under these conditions, be determined by changes in the demand for money, less domestic credit expansion and the trade balance. The correspondence is not exact, because Kouri and Porter (1974) use a discrete time specification and impose rather than estimate rapid adjustment in the money market, but models 4 and 5 could be viewed as partial adjustment, continuous time analogues of the model in their study.
Parameter estimates and test statistics for models 4 and 5 are given in Appendix C. Table 4.1 summarises the test statistics for several key variables.
| VARIABLE, TEST STATISTICS | MODEL 1 | MODEL 4 | MODEL 5 |
|---|---|---|---|
| y – r2 | .2637 | .2304 | .2729 |
| – RMSPE1 (%) | 2.2 | 2.1 | 2.3 |
| – RMSPE2 (%) | 2.6 | 2.6 | 2.8 |
| P – r2 | .4857 | .4300 | .4628 |
| – RMSPE1 (%) | 1.0 | 1.0 | 1.0 |
| – RMSPE2 (%) | 3.2 | 7.4 | 6.8 |
| R – r2 | .4365 | .0264 | .0933 |
| – RMSPE1 (%) | 5.5 | 8.0 | 7.4 |
| – RMSPE2 (%) | 19.9 | 35.8 | 33.7 |
| M – r2 | .7194 | .0000 | .4060 |
| – RMSPE1 (%) | .6 | 1.1 | .9 |
| – RMSPE2 (%) | 5.2 | 6.6 | 6.7 |
There are several noteworthy features of these results. Firstly, the partial adjustment
parameter (α26) from the money equation (8a) is negative in model 4 and
very small in model 5. Both results reject the hypothesis that adjustment in financial
markets is so rapid that economic agents remain on the demand for money function
continuously or achieve their desired real balances within the observation period. Secondly,
in model 4, the interest rate effects represented by β3
and β4 are estimated at close to their values in model 1. In model 5 the
same parameters, whan estimated indirectly in equations 1, 3, 4, 6 and 7 are of the expected
sign and significant, but the same parameters estimated as β3
and β4 only in equation 8 assume highly implausible values. The parameter on
the term reflecting exchange rate expectations 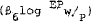 is small and
insignificant in both models whereas in model 1 this term is strongly significant.[40]
Thirdly, in model 4 γ3 is positive and significant. These results suggest
that the way in which the quantity of money is determined in models 4 and 5 is misspecified,
as the specification is having adverse effects on what are well determined parameters in the
standard version of the model.
is small and
insignificant in both models whereas in model 1 this term is strongly significant.[40]
Thirdly, in model 4 γ3 is positive and significant. These results suggest
that the way in which the quantity of money is determined in models 4 and 5 is misspecified,
as the specification is having adverse effects on what are well determined parameters in the
standard version of the model.
A final observation that can be made concerns the poor relative performance of the money and foreign reserves equations. As noted above, this is the result which one would expect if the residual asset in the monetary sector is misspecified in models 4 and 5 as compared with model 1. Overall these results appear to confirm that the usual methods of estimating the demand for money function are inappropriate in the Australian economy and in the context of this model.
Footnotes
The second method is econometrically inappropriate, but the results may be of interest to any who regard model 4 as misspecified by the inclusion of γ1, y3, y4, y6 and y7. [37]
In these models money shifts from being the residual asset. If, however, money is the true residual asset, then one may expect the performances of the foreign reserves and money equations to deteriorate. [38]
When estimated in equation 8 of model 5, β6* is very large but of the wrong sign. [40]