RBA Annual Conference – 2003 Stock Market Volatility and Monetary Policy: What the Historical Record Shows Barry Eichengreen and Hui Tong[1]
1. Introduction
This paper presents a fact – we are tempted to say a ‘new fact’, since to our knowledge it has not been recognised before. The fact is that stock market volatility, when viewed from a long-term perspective, tends to display a u-shaped pattern.[2] When we take data spanning the 20th century for today's now-advanced economies – all of the economies for which such a long time series of financial data are available – we generally see that volatility first falls at the beginning of the period before stabilising and then rising in recent years.[3]
Any blanket generalisation about financial market behaviour is problematic when one attempts to apply it to a significant number of countries. There are exceptions to the rule, as noted below. But there is some evidence of the u-shaped pattern in a substantial majority of the countries we consider.
Our interpretation of this pattern is as follows. The decline in volatility in the early, pre-World War I period reflects ongoing improvements in the information and contracting environment, which find reflection in the improved operation of financial markets. Indeed, there is a considerable literature on the growth and development of financial markets in this period, although it has paid relatively little attention to stock markets, given their still limited role in resource allocation. Following the Great Depression of the 1930s, there was then a period of tight regulation of financial markets and institutions, one consequence of which was limited volatility (with some sharp exceptions, such as during World War II). The subsequent rise in volatility reflects financial liberalisation inadequately supported by prudential control; an increase in the instability of macroeconomic policies, especially following the breakdown of the Bretton Woods System; and financial globalisation, which may have been a factor in rising volatility in some countries.[4]
Changes in asset prices are not a bad thing in and of themselves. They convey signals to investors about changes in likely future outcomes and their implications for resource allocation. They reflect changes in the price of risk, responding to changes in the risk to which the economy is subject and/or the tolerance of investors for holding it. At the same time, to the extent that the volatility of asset prices reflects the volatility of policy, more volatility may be an indication of a deteriorating policy environment. Similarly, to the extent that the volatility of asset prices is indicative of the limited ability of banks and firms to manage risk, reflecting inter alia inadequate capitalisation or diversification, more volatility may be an indication of such problems. Our evidence provides some support for both the positive and negative interpretations of volatility trends over time.
2. The Fact
There are several common ways of estimating volatility. In the present context, all of them produce similar results. Specifically, all of them produce evidence of a u-shaped pattern.
A first approach is to compute the standard deviation of returns over successive periods of time – for example, to take end-of-month data for the 12 months of the year and calculate volatility as the standard deviation of those 12-monthly observations, and then to roll the window forward in time (drop month 1 and add month 13). An application of this method is Officer (1973). A potential problem with Officer's approach is that the use of overlapping observations will create a correlation between standard deviations at different points in time.[5] An alternative is to use non-overlapping observations: to compute the standard deviation using, say, months 1 through 12, 13 through 24, and so forth. The problem here is that the periodisation is arbitrary and the result is relatively few data points. In practice, however, we obtain extremely similar results using the two approaches.
An alternative is to specify a parametric model of asset returns and to use it to derive estimates of volatility. Based on the observation of serially correlated volatility, Bollerslev (1986) suggested the Generalised AutoRegressive Conditionally Heteroskedastic (GARCH) model as a basis for deriving such estimates. The GARCH model starts by specifying an equation for the conditional mean of stock returns. Because the current stock return may depend on past stock returns, the equation for the mean is specified to allow for intertemporal dependence:
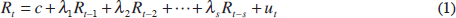
where Rt is the stock return at time t, c is a constant term, and ut is the disturbance. The disturbance is modelled as:

where vt has the i.i.d. normal distribution with zero mean and unit variance, and ht evolves according to:
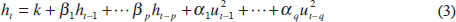
This is the GARCH (p,q) model, where the equations for the conditional mean and variance
can be jointly estimated using maximum likelihood. The GARCH (1,1) model is
commonly used in empirical applications because it does not require estimation
of many coefficients and seems to capture return dynamics relatively
well.[6]
In the GARCH (1,1) model, α (in Equation (3) above) measures
the extent to which a volatility shock today translates into volatility tomorrow,
while α+β measures the rate at which volatility dissipates
over time. If (α+β)<1, then 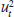 will be covariance stationary, and the unconditional
mean of
will be covariance stationary, and the unconditional
mean of 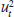 will be:
will be:

Lee and Hansen (1994) discuss the asymptotic distribution of the GARCH (1,1) maximum likelihood estimator when (α+β)<1. However, (α+β)>=1 (the case where the effects of volatility shocks are permanent) can also occur in practice. In Bekaert and Harvey (1997), the study closest in spirit to our own, half of the stock markets considered have estimated values such that α+β >=1.[7]
One possible solution to this problem is to add deterministic time trends, f(t), to the volatility equation of the GARCH (1,1) model:

Specifically, we add a linear combination of time and the square root of time. Standard arguments suggest that the estimated coefficients for the time terms will be consistent, assuming of course that their addition eliminates the unit root problem.[8]
We analyse the stock markets of 12 now-developed countries using time series from Global Financial Data (GFD). The countries are Australia, Canada, Denmark, Finland, France, Italy, Japan, New Zealand, Sweden, Switzerland, United Kingdom and the United States. We have monthly data (end-of-month closes, as calculated by central banks, national statistical agencies, or stock exchanges themselves).[9] The end-of-month return data are calculated for each of these countries from the late 19th or early 20th century to 2002. Details are in Table 1.
| Country | Monthly stock index period |
Yearly stock index starting date |
Return index starting date |
|---|---|---|---|
| Australia | 1875–2003 | 1875 | 1882 |
| Canada | 1918–2003 | 1915 | 1933 |
| Denmark | 1921–2003 | 1914 | 1969 |
| Finland | 1922–2003 | 1922 | 1961 |
| France | 1895–2003 | 1856 | 1895 |
| Italy | 1906–2003 | 1906 | 1924 |
| Japan | 1914–2003 | 1914 | 1920 |
| New Zealand | 1931–2003 | 1926 | 1986 |
| Sweden | 1906–2003 | 1901 | 1918 |
| Switzerland | 1916–2003 | 1910 | 1966 |
| UK | 1694–2003 | 1694 | 1694 |
| US | 1800–2003 | 1800 | 1802 |
|
Source: Global Financial Data, Inc. |
|||
Ideally, we would like to measure stock market volatility in terms of total returns (inclusive of both price changes and dividends). Unfortunately, information on dividends for the earlier period is fragmentary. We therefore construct the return series as the log-difference of the stock price index. This is not ideal, but it is the same procedure followed in other historical studies, e.g. Jorion and Goetzmann (1999). We subtract the rate of currency depreciation relative to the US dollar and the US inflation rate in order to express all returns in constant dollar terms.[10]
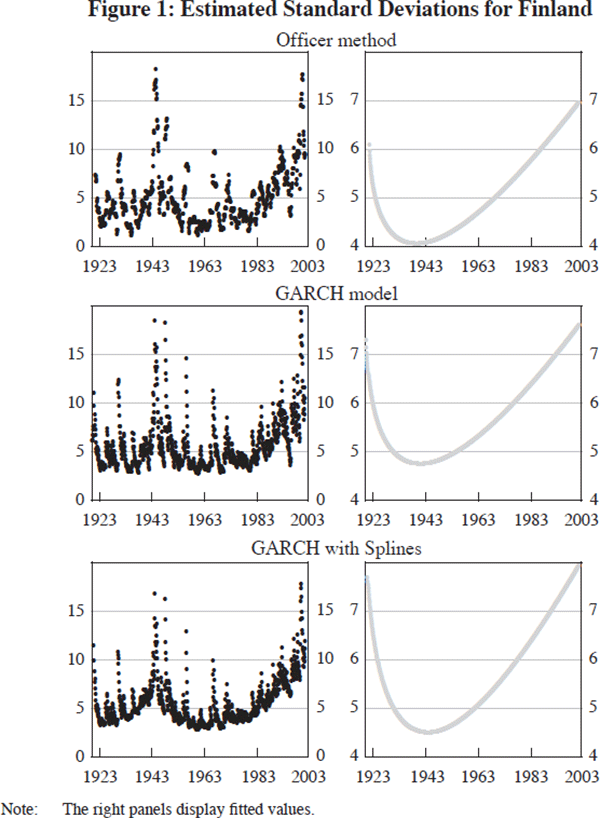
We can illustrate the method with reference to a specific country, Finland, the data for which yield relatively clean results.[11] We start with the familiar Officer method. We estimate the stock return standard deviation for month 1 to month 12, next estimate the standard deviation from month 2 to month 13, and then repeat the procedure, rolling the sample forward continuously. The estimated conditional standard deviation appears to fall in the early part of the sample before rising again in recent decades (see the left-hand side of the first row of Figure 1). This resembles a quadratic to the naked eye (at least to our eyes). To make our ocular econometrics more precise, we can fit a quadratic time trend to the estimated volatilities; doing so yields a u-shape (see the right-hand side of the first row of Figure 1). The estimated coefficients are in the first column of Table 2, where the quadratic form is:
| Quadratic with Officer method(a) | GARCH (1,1)(b) | Quadratic(c) | Deterministic trends(d) | Splines(e) | Quadratic with Splines(f) | |
|---|---|---|---|---|---|---|
| Number of observations | 940 | 940 | 940 | 940 | 940 | 940 |
| Wald χ2 (6) | 46.77 | 151.21 | 33.81 | 133.61 | 108.95 | 92.96 |
| Stock return (one lag) |
0.273 (0.036) |
0.2626 (0.0357) |
0.2626 (0.0397) |
|||
| Stock return (two lag) |
−0.011 (0.035) |
−0.0110 (0.0365) |
0.0197 (0.0378) |
|||
| Stock return (three lag) |
0.059 (0.032) |
0.0434 (0.0402) |
0.0268 (0.0401) |
|||
| Stock return (four lag) |
0.022 (0.032) |
0.0050 (0.0355) |
0.0268 (0.0341) |
|||
| Stock return (five lag) |
0.111 (0.030) |
0.0786 (0.0372) |
0.0798 (0.0341) |
|||
| Stock return (six lag) |
0.093 (0.031) |
0.0964 (0.0350) |
0.1136 (0.0299) |
|||
| Constant | 0.205 (0.150) |
0.1863 (0.1532) |
0.2101 (0.1558) |
|||
| t11 | 0.0126 (0.0019) |
0.0121 (0.0018) |
0.5797 (0.8217) |
0.0205 (0.0065) |
0.0148 (0.0015) |
|
| t12 | 0.0385 (0.0042) |
|||||
| t13 | −0.3926 (0.0726) |
−0.3771 (0.0658) |
−0.0835 (0.1036) |
−0.3577 (0.1553) |
−0.4650 (0.0562) |
|
| t14 | −1.7810 (0.1987) |
|||||
| k | 7.0982 (0.6537) |
1.587 (0.274) |
7.6689 (0.5010) |
−1.3261 (2.8297) |
2.5758 (0.9753) |
8.1081 (0.5014) |
| α | 0.210 (0.025) |
0.2203 (0.0282) |
0.1957 (0.0334) |
|||
| β | 0.767 (0.025) |
0.7632 (0.0285) |
0.6761 (0.0479) |
|||
| (a) Officer method (b) GARCH (1,1) model with ω1 = ω2 = 0 (c) Fitting the estimated standard deviation from the GARCH (1,1) model onto a quadratic form (d) GARCH (1,1) model without restricting ω1 = ω2 = 0 (e) GARCH (1,1) model without restricting ω1 = ω2 = 0, adding Spline function (f) Estimated standard deviation from GARCH (1,1) model with Spline function fitted onto a quadratic form |
||||||

Both coefficients are significantly different from zero (the p-values are less than 0.01). This means that a quadratic fits the data significantly better than a constant term or a linear trend. The signs clearly suggest a u-shape.[12]
Alternatively, we can estimate the standard GARCH (1,1) model, starting with the volatility equation:

The result is in the second column of Table 2. On the left-hand side of the second row of Figure 1 we plot the estimated standard deviation series against time. Again, the series resembles a quadratic to the naked eye. Once more we can fit a quadratic to these estimates of volatility:

where ω1 and ω2 are the estimated coefficients on time and its square root, as before. And, once more, a quadratic time trend fits the estimated volatilities relatively well. The third column of Table 2 shows that both coefficients are significantly different from zero (the p-values are less than 0.01). The right-hand side of the second row of Figure 1 plots these fitted values.
The estimated value of α+β, at 0.976, is close to unity, and we cannot reject the hypothesis that it equals one.[13] In order to eliminate the unit root, we add deterministic time trends to the volatility equation of the GARCH (1,1) model:
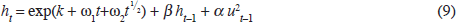
However, α+β is still close to 1 (see the fourth column of Table 2). We address this problem by supplementing GARCH (1,1) model with Spline functions. Since the Officer method provides a general picture of the volatility process, we use it to guide the fitting of Splines. Figure 1 suggests that volatility rose significantly during World War II and dropped sharply following its conclusion. This implies that controlling separately for this period may eliminate the unit root. Adding a World War II dummy variable (D1t) to the volatility specification function entails estimating a model of the form:
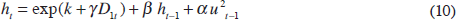
But estimating Equation (10) would be tantamount to assuming no trend during World War II and that there were discontinuities in the volatility process at the start and the end of that event. Figure 1 suggests, in contrast, that volatility rose gradually during World War II and dropped gradually following its conclusion, instead of jumping up, remaining constant at this higher level during the war, and then jumping back down following the armistice. We therefore introduce a Spline function for the time trend in the volatility specification. Applying a Spline function with one break/cut-off point to:
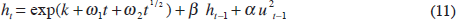
is the same as estimating:
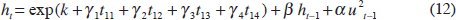
We divide the sample into halves in August 1945 (the end of World War II). t11 is equal to t until the observation for August 1945.[14] The Spline method ensures that the volatility process will be continuous. For each of the two periods (before and after August 1945), we fit a quadratic to allow for the possibility that volatility may not follow a linear trend. The conditional maximum likelihood estimates of the parameters are reported in the fifth column of Table 2. The time trend constructed from:
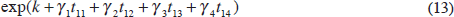
suggests that there is a quadratic form for each period. The end-point of the first quadratic form and the starting point of the second necessarily meet in August 1945. The standard deviation of the fitted returns is shown on the left side of the third row of Figure 1.
In the fifth column of Table 2, the unit root has disappeared. The estimated value of α+β, at 0.872, is significantly different from unity at the 1 per cent confidence level.[15] Again, we may want to ask whether we can fit a single quadratic form to the estimated standard deviation series. Ordinary least squares suggests that the answer is yes (see the sixth column of Table 2 and the right-hand side of the third row of Figure 1).
A key point is that we obtain very similar results using alternative methods, as will be evident from comparing the three rows of Figure 1. No method is perfect. The Officer method is unparameterised, and the division of the sample into periods is arbitrary. The standard GARCH model suffers from unit root problems, which raise questions about whether the estimated parameters are distributed normally and estimated consistently. The GARCH model with Splines requires us to make a choice between the convergence rate and singularity (see footnote 8). But, as Figure 1 shows, the three methods produce very similar estimates of the standard deviation of returns. Importantly for our purposes, those estimates are all consistent with very similar estimates of the u-shaped intertemporal pattern. Different readers will prefer different empirical approaches. Our own preference is the GARCH (1,1) model with Splines. But the choice makes little difference for our central finding.
We now apply this approach to other countries. When we estimate the simple GARCH (1,1) model, we find that the unit root problem (α+β>=1) is present virtually everywhere.[16] We then use Officer's method to obtain a general picture of stock return volatility. Next we fit Spline functions to the GARCH (1,1) model, with the Spline function cut-off points being the peaks in volatility as estimated using Officer's method.[17] In the GARCH (1,1) model with Splines, α+β is significantly less than 1 at the 2 per cent level, according to the standard χ2 test, for all 11 additional countries.[18]
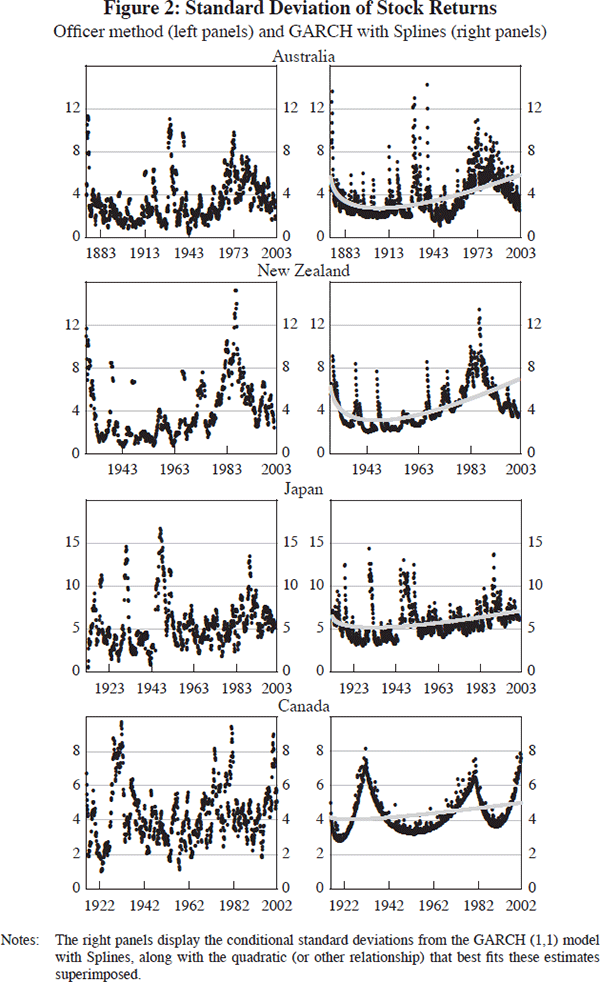
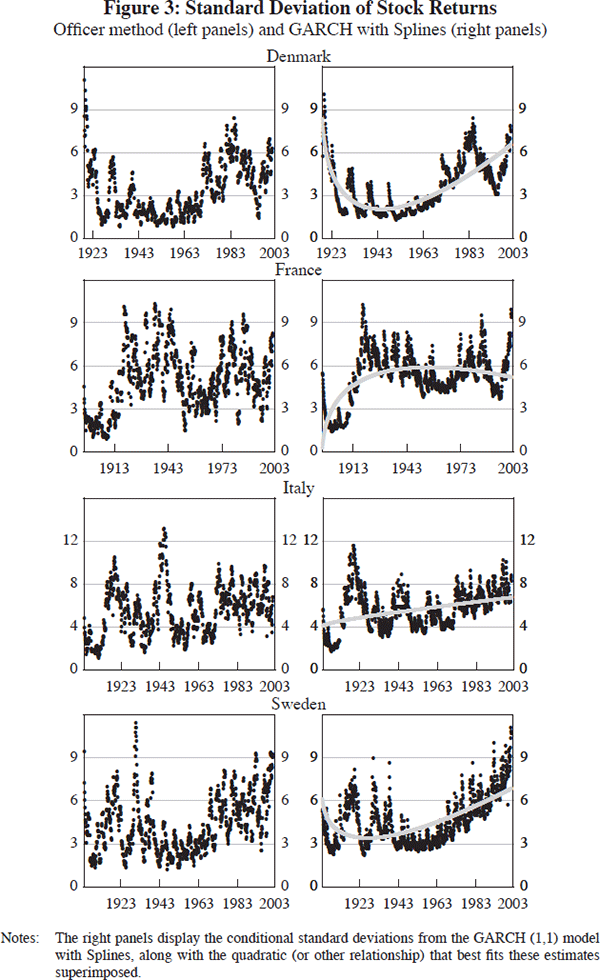
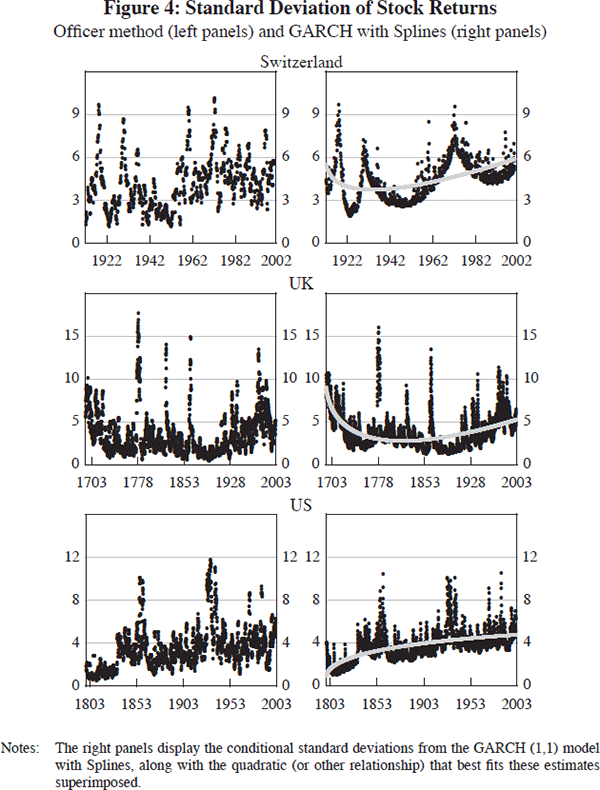
The results using the GARCH (1,1) model with Splines are summarised in Figures 2–4 and Tables 3, 4 and 5. The figures contain two panels for each country. The one on the left displays the estimated conditional standard deviations obtained using the Officer method (which we use as guidance for fitting Splines). The one on the right shows the conditional standard deviations from the GARCH (1,1) model with Splines, with the quadratic (or other relationship) that best fits these estimates superimposed.[19]
| Country | Early years | Recent years | Unit root before pline |
Unit root after Spline |
u-shape? |
|---|---|---|---|---|---|
| Australia | Dropping | Increasing, then dropping | Yes | No | Yes |
| Canada | Dropping | Increasing | Yes | Not severe | Yes, but poorly determined |
| Denmark | Dropping | Increasing | Yes | No | Yes |
| Finland | Dropping | Increasing | Yes | No | Yes |
| France | Dropping | Increasing | Yes | Not severe | Inverted u-shape |
| Italy | Dropping | Increasing | Yes | Not severe | Monotonically increasing |
| Japan | Dropping | Increasing | No | No | Yes |
| New Zealand | Dropping | Increasing, then dropping | Yes | No | Yes |
| Sweden | Dropping | Increasing | Yes | Not severe | Yes |
| Switzerland | Increasing | Increasing | Yes | No | Yes |
| UK | Dropping | Dropping, then increasing | Yes | No | Yes |
| US | Dropping | Increasing | Yes | No | Inverted u-shape |
|
Source: Authors' calculations |
|||||
The following aspects of stock market returns may be of particular interest.
- The estimated coefficients. Consider, to take a country not entirely at random, Australia. The estimates of the equation for the mean return indicate that the one-period lagged stock return affects the current stock return: the coefficient for the one-period lagged stock return is 0.116, with a standard error of 0.031, which is thus significantly different from 1 (see Table 3). This is an unexceptional level of persistence; the analogous coefficients are higher in about half of our countries and lower in the other half. The estimates of the volatility equation suggest that the Spline functions are important. (Recall that t1, t2, and t3 are the three Spline components for the linear time trend t, while (t0.5)1, (t0.5)2, and (t0.5)3 are the three Spline components for the non-linear time trend (t0.5). By construction, the cut-off points/dates for the Spline components are the same for t and (t0.5).) For Australia, the coefficient on t1 is 0.005, with a standard error of 0.002, which is thus significantly different from zero. α+β, the persistence of volatility shocks, is 0.908. This is an unexceptional level of volatility persistence by international standards. A χ2 test of the unit-root hypothesis (α+β=1) gives a test statistic of 47.87, which suggests that the unit root is rejected at all reasonable significance levels.
- The trend of volatility. This is constructed from the coefficients for the time functions t and t0.5.
- Changes in the trend in different sub-periods. These can be seen from the estimated stock return standard deviation.[20]
- The u-shape. Finally, we can analyse whether the estimated standard deviation can be fitted on a quadratic form.[21] The results, in Table 4, are consistent with a u-shape in 8 of the 11 countries included there, in that the coefficient on time is positive and that on the square root of time is negative. Adding Finland, where we already detected a u-shape in Table 2, we thus find evidence of this pattern in 9 of our 12 countries (the exceptions being France, Italy and the US).[22] With the exception of Canada, the coefficients on both time and its square root are significantly different from zero at standard confidence levels.[23] The findings are summarised in Table 5.
Two interesting variations on this theme are Australia and New Zealand, which conform to the general pattern but display some tendency for volatility to drop back down in recent years. This is easiest to see in the left-hand side of Figure 2, where we show the Officer estimates. We will have more to say about this pattern below.
An obvious question is whether very recent volatility (the ‘high-tech bubble’ at the end of the sample period) is responsible for our finding of a u-shaped pattern. Is it possible that, absent this exceptional episode, we would find evidence of secularly declining volatility, reflecting improvements in market institutions and regulatory quality as the now-advanced industrial countries matured? To get at this question, we omitted the data for the post-1997 period. The basic results, including the evidence of a u-shaped pattern, remained unchanged.
We also wondered whether evidence of rising volatility of US dollar returns for countries other than the United States is being driven by the increasingly volatility of the dollar exchange rate. (Recall that we convert own-currency returns into US dollars.) In fact, when we instead compute real returns in own currency (deflating them by the national price index), we obtain very similar results.[24]
We also estimated the GARCH(1,1) model with Splines for 11 emerging markets (so identified by IMF (2003)): Argentina, Brazil, Chile, the Czech Republic, Hong Kong, Hungary, Malaysia, Poland, Singapore, South Korea and Thailand. The data are weekly, starting in the 1960s or 1970s. This paper's findings are summarised in Table 6. These suggest that volatility dropped in the early stages of stock market development and dropped further in recent years. It is tempting to characterise the countries as still on the downward-sloping arm of the intertemporal u. But patterns in these countries are diverse and difficult to generalise about. We suspect that it will be necessary to wait for more historical data before accepting or rejecting the hypothesis of a u-shaped pattern.
| Country | Early years | Recent years | Unit root after Spline | Unit root before Spline | u-shape |
|---|---|---|---|---|---|
| Chile | Dropping | Dropping | No | No | Decreasing time trend |
| Argentina | Dropping for the first year | Dropping | No | Weak unit root | Inverted u-shape |
| Singapore | Dropping for the first year | Dropping | No | No | Constant |
| Brazil | Dropping for the first two years | Increasing | No | Yes | Increasing time trend |
| Thailand | Dropping for the first two years | Dropping | No | Weak unit root | Increasing time trend |
| South Korea | Dropping | Dropping | No | Weak unit root | u-shape |
| Czech Republic | Dropping | Dropping | No | No | u-shape |
| Poland | Dropping | Dropping | No | Yes | Decreasing time trend |
| Hungary | Dropping for the first half year | Constant | No | Yes | Inverted u-shape |
| Malaysia | Dropping | Dropping | No | No | Dropping first, then staying constant |
| Hong Kong | Dropping | Dropping | No | Yes | Inverted u-shape |
|
Source: Authors' calculations |
|||||
3. Explanations
Having presented evidence of a u-shaped pattern for stock market volatility in the advanced economies, we now turn to the question of why it obtains. The obvious answer is changes in the volatility of the economy and the volatility of policy. But Schwert (1989b), analysing a long-time series of historical data like us (but in his case focusing exclusively on the United States), found only weak evidence that stock market volatility is associated with the volatility of the economy. Although he found that both stock returns and output are more volatile in recessions, which can explain why volatility is higher in some periods than others, the additional volatility of activity in such periods appears to be insufficient to explain the additional volatility in asset markets. The point is most obvious for episodes like the Great Depression of the 1930s, but it is more general. In terms of this paper's finding, the point can be put as follows. Most investigators agree that there has been a secular decline in macroeconomic volatility in the now-advanced economies.[25] But while this decline in output volatility has been broadly linear, the same has not been true of stock market volatility.[26] Thus, it is hard to see how the former can explain the latter. At a minimum, other factors must also be at work.
These observations have led researchers in two directions.[27] Schwert (1989b) himself posited that there might be increasing uncertainty about policy and performance in certain periods (he emphasised periods of slow growth and recession). Thus, the rise in stock market volatility in such periods could reflect not just the actual increase in the volatility of the economy but the even greater increase in expected volatility (and dispersion of expectations).[28] Volatility could thus be driven by a small and changing probability of extreme events (the collapse of markets in the Great Depression, for example), events that may not in fact be observed in the sample period.[29] Schwert (1989a) also suggested that bank failures and related forms of financial distress are more prevalent in such periods and that these events are associated with stock market volatility, both because they disrupt the operation of the financial system (including the stock market) and because they raise the probability of sharp policy changes in response. But while Schwert's mechanism can amplify the relationship between output volatility and stock market volatility (if expectations of the former are extrapolative), it cannot obviously explain the nonlinear pattern in volatility levels that we observe.
Subsequent authors challenged Schwert's conclusion that changes in stock market volatility cannot be adequately explained by observed changes in macroeconomic policies and conditions. In effect, they responded by introducing additional macroeconomic variables. Binder and Merges (2001) regressed the volatility of the US S&P Composite Index on measures of monetary uncertainty, the risk premium, and the risk-free rate. All of these variables entered with significant coefficients. In effect, they reversed Schwert's conclusion by augmenting his list of macroeconomic variables to include additional monetary and financial factors. Similarly, Errunza and Hogan (1995) show that the variability of European returns is associated not just with the fluctuation of output but also with that of money supplies. They argue that the two factors – macroeconomic volatility and financial volatility – go a long way together toward explaining observed stock market volatility.[30]
Other authors extended this approach by introducing a role for financial integration. Kose, Prasad and Terrones (2003) suggest that financial integration (due mainly to the removal of capital controls) is responsible for an increase in the relative volatility of consumption and asset returns, especially in countries that have liberalised their capital accounts only relatively recently and partially. When negative shocks hit these countries, these authors observe, they tend to lose access to international capital markets. The rapid reversal of capital flows in response to these events amplifies the volatility of their consumption and asset market outcomes.[31] Dellas and Hess (2002), on the other hand, find that the removal of capital controls is associated with less output and stock market volatility. This runs counter to the thesis that financial integration increases stock market volatility.[32]
A possible reconciliation may be as follows. Kose et al find that consumption and financial market volatility rise with financial liberalisation mainly in countries that have liberalised only partially and relatively recently – that is, in low- and middle-income countries.[33] This suggests that the dominant effect of the removal of capital controls in high-income countries is to enhance the liquidity, depth and efficiency of financial markets.[34] In low-income countries, in contrast, the main effect of the removal of capital controls is to expose the economy to sudden stops, exacerbating consumption and financial volatility.[35]
In what follows we focus on the role of monetary policy and international financial integration in explaining the u-shaped time profile of stock market volatility. We privilege monetary policy because it is the subject of this conference.[36] We focus on financial globalisation because, like stock market volatility, it also displays a u-shaped pattern; it has been high when stock market volatility has been high (toward the end of the 19th century and again in recent years).[37] There also is Calvo and Mendoza's (2000) conjecture that the globalisation of financial markets has reduced the incentive for investors to assemble and process information about individual market conditions, resulting in greater volatility.[38]
The additional data are from the Bordo et al (2001) database, suitably updated.[39] The first step is to estimate the annual standard deviation of the money supply as in Schwert (1989b, p 1117). For most countries we have only annual money stock estimates (quasi M2) for the entire period.[40] We therefore implement the following procedure:
-
We estimate a 2nd-order autoregression for the money supply growth rate mt,
using all the annual data available:

where µmt is the disturbance term.
-
We then estimate a 2nd-order autoregression for the absolute values of the errors
from the regression in Equation (14),
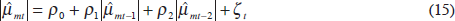
-
The fitted values
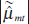 from Equation (15) estimate the conditional standard
deviation of mt, given information available before time
t. We impute the monthly standard deviation by dividing the annual
standard deviation by the square root of
12.[41]
from Equation (15) estimate the conditional standard
deviation of mt, given information available before time
t. We impute the monthly standard deviation by dividing the annual
standard deviation by the square root of
12.[41]
To estimate the effect of monetary volatility on the stock return deviation, we follow Schwert (1989b, p 1144) by estimating an ordinary least squares regression of the form:

where 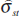 is the stock return standard deviation estimated
from our GARCH model with Splines, c is the constant term,
is the stock return standard deviation estimated
from our GARCH model with Splines, c is the constant term, 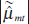 is the fitted standard deviation of the money supply
growth rate, and Dct
is the capital control indicator.
is the fitted standard deviation of the money supply
growth rate, and Dct
is the capital control indicator.
The results, in Table 7, show that the volatility of money supplies, and by implication the instability of the monetary regime, enters positively as a determinant of stock market volatility in 10 of 11 country cases, and that it is a significant determinant of stock market volatility in every country but one.[42] Thus, we have here at least one potential explanation for changes over time in stock market volatility. In particular, the increase in monetary volatility in many countries in the 1970s and 1980s may be part of the explanation for the rise in stock market volatility in these decades.[43] Similarly, that there is a spike in stock market volatility in the 1930s, most notably in the United States, is consistent with this conclusion, given the large literature emphasising the role of unstable monetary policies in the Great Depression. Note further that while Australia's stock market volatility broadly follows the u-shaped pattern common to other countries, there is also evidence of volatility dropping relative to earlier levels in recent years.
It is not clear what lies behind this recent trend in Australia. The decline in stock market volatility roughly coincides with the RBA's shift to an inflation-targeting regime and the associated decline in monetary volatility, although the downward trend in stock market volatility seems to predate the switch to inflation targeting, which suggests that the change in monetary policy operating strategy may not have been all that was going on.[44] Other possibilities include strengthened supervision and regulation (the fall in leverage following the boom period analysed by Simon, (this volume)), the reduction in the underlying volatility of the economy associated with Australia's diversification out of natural resources, and the growth of the stock market itself, which may have increased the representation of relatively small, relatively volatile firms.[45]
Another result from Table 7 is that the dummy variable for the presence of capital controls enters with a negative coefficient in 7 of 10 cases and differs significantly from zero for all 10 countries.[46] A negative coefficient is consistent with the view that financial internationalisation is associated with stock market volatility. Thus, the fact that capital accounts were open both in the late 19th century and in recent years may be part of the explanation for why stock market volatility was relatively high at the beginning and end of our period – for why we observe a u-shaped pattern in volatility.
But three countries deviate from this pattern: in their cases the coefficient in question is significantly positive. The data seem to be telling us that the effects of financial openness on financial volatility are more complex and contingent than those of monetary policy – not surprisingly insofar as this is what both policy-makers and the recent literature have been telling us as well.[47] Thus, the contingent nature of the effects of financial openness may be what we are picking up in the present results.
This audience may be particularly interested that controls are positively associated with volatility in Australia: the estimates suggest that for this country financial globalisation has been a stabilising force. We obtain this result both using annual data for 12 decades and monthly data for the period since 1957.
These findings are robust to a variety of sensitivity analyses. The results using monthly data, which are available for this group of sample countries starting in the 1950s, are similar to those reported above. We obtain the same variety of coefficients on capital controls as for the longer period. And in all cases we obtain the same positive coefficient for monetary volatility as when we use annual money stock data for the longer period.[48]
A further form of sensitivity analysis is to compare the results for the period when monthly data become available using annual data (that is, eliminating the annual observations for preceding decades, which means that all differences are attributable to the periodicity of the data and not the time span covered). When we do this, we again obtain qualitatively similar results. In the case of Australia, for example, the coefficients on monetary volatility and capital controls both keep their positive signs when we use annual data starting in 1957, and both coefficients remain statistically significant at the 95 per cent confidence level.
For two countries, the United States and the United Kingdom, we also have consistent monthly money supply series for longer historical periods. For the US, we have monthly M2 data starting in 1907 from Friedman and Schwartz (1963); for the UK, we have monthly data starting in 1880 from Capie and Wood (1985). Estimates using these monthly series yield similar results to before (see Table 8).
Finally, we substituted alternative estimates of the dependent variable (the conditional standard deviation of the stock market return). For example, we constructed the dependent variable using the Officer method instead of the GARCH model with Splines. Again, the results were very similar.
Together, these sensitivity analyses reassure us that our findings on the connections between monetary volatility and stock market volatility are not a product of the particular way in which we estimate the conditional standard deviation of the stock market return. They are not a figment of annual data. Nor are they entirely driven by the exceptional volatility of the 1930s.
Two further comments on money supply volatility are important in this context. First, the rise in monetary volatility following the breakdown of the Bretton Woods System, which removed the only existing orientation for monetary policy in many countries, has been widely remarked upon (see DeLong (1996) and Sargent (1999)). Comparing 1945–1970 with subsequent years, we see an increase in the volatility of monetary policy, as measured by Equation (15), in 9 of our 11 countries.[49] In retrospect, that this should contribute to greater stock market volatility is hardly surprising.
Second, the idea that the pre-1913 period was one of monetary volatility may surprise readers familiar with the gold-based monetary arrangements of the time, which limited the scope for discretionary policy. But the gold standard was also marked by not infrequent crises, which affected the currency/deposit multiplier, and by periodic gold discoveries. Moreover, money supply under the gold standard was at least partly endogenous; it responded to output fluctuations, as under any fixed exchange rate regime. To the extent that output was more volatile before 1913 than after 1945, so too would have been money supply, ceteris paribus.[50] Whatever the explanation, in 5 of the 10 countries for which we have sufficient annual data to make the comparison, the standard deviation of the money supply (again estimated following Equation (15) above) was larger before 1914 than in 1945–1970.[51]
One way of gaining purchase on these questions is to replace our measure of monetary volatility with dummy variables for the exchange rate regime.[52] We adopt the standard tripartite distinction of fixed rates, intermediate regimes, and flexible rates. The results are shown in Tables 9 and 10. Consider again the case of Australia. The coefficients on both fixed and intermediate regimes are negative (compared to the omitted alternative, of flexible regimes) and statistically significant at standard confidence levels. In addition, the coefficient on capital controls remains positive as before. When we include the two exchange rate regime measures and our measure of monetary volatility in the same equation (in Table 10), each of these variables matters.
We obtain similar results for other countries, with one important exception, namely that in the majority of cases we obtain a positive coefficient for intermediate exchange rate regimes. This is consistent with the scepticism of many observers (including one of the present authors) of the durability and credibility of such regimes. If intermediate regimes do not effectively constrain potentially erratic monetary policies, they will not be associated with low levels of stock market volatility, other things equal. There is now a large literature questioning whether the constraint they impose is effective.
The volatility of the money supply retains its significance in the vast majority of sample countries. In other words, while events like the breakdown of the gold standard following World War I and subsequent interlude of floating or the breakdown of the Bretton Woods System and the subsequent shift to flexible rates may partly explain the rise in stock market volatility in the 1920s and 1970s, they are not the entire story; the shift to floating implied a greater increase in monetary volatility in some countries than others, and this is being picked up by the additional effect of the standard deviation of money supplies even after controlling for the change in exchange rate regime. Our interpretation of this finding is that if the exchange rate anchor for monetary policy is removed, then it is important to put an alternative anchor for policy in its place in order to avoid amplifying financial volatility.[53]
4. Conclusions
In this paper we have studied the volatility of stock markets in the long run. We first established that volatility has not been constant. For the majority of countries we consider, there is evidence of a u-shaped pattern, with volatility first falling before turning back up in recent decades. The early decline is explicable in terms of improvements in the information and contracting environment – that is, in terms of the development of financial markets during the initial phases of modern economic growth. The recent rise is more disturbing and controversial.
We then considered the roles of monetary policy and financial internationalisation, two candidates for explaining these trends. We found a positive association of monetary volatility with stock market volatility; an interpretation is that the conduct of monetary policy and the nature of the monetary regime are important for stock market volatility. That monetary policy became increasingly volatile in a number of countries in the 1970s and 1980s thus may be part of the explanation for why stock markets have been more volatile in recent decades.
Probing deeper, we found that fixed exchange rate regimes are associated with relatively low levels of stock market volatility, flexible exchange rate regimes with relatively high ones. This makes it tempting to conclude that the collapse of currency pegs and the transition to floating explain the recent rise in stock market volatility. But not only the official exchange rate regime but also the conduct of monetary policy under that regime appear to matter, in that we find a positive effect of monetary volatility on stock market volatility even after controlling for the exchange rate regime. Not just the putative exchange rate regime matters for the volatility of financial market outcomes, in other words; also important is the credibility and conduct of monetary policy under that regime.
We further find, for the majority of countries considered, that financial internationalisation is positively associated with stock market volatility. That international financial markets were open both in the late 19th century and in recent decades thus may be another part of the explanation for why we observe a u-shaped pattern in stock market volatility. This interpretation is consistent with Calvo and Mendoza's (2000) conjecture that the globalisation of financial markets has reduced the incentive for investors to assemble and process information about individual market conditions, resulting in greater financial volatility. But it is important to emphasise the existence of a substantial minority of countries – including Australia – where financial internationalisation does not display this association. In these countries, financial openness is associated with less stock market volatility, not more. The only safe conclusion may be that the effects of international financial openness are complex and contingent – something which careful observers will already have concluded from the experience of recent years.
For Australia, our host country, we find some evidence of a u-shaped pattern in stock market volatility but also signs of a decline in volatility in the 1980s and 1990s. This break coincides with the removal of capital controls and with a decline in monetary volatility associated with the adoption by the Reserve Bank of its inflation-targeting strategy. We thus see Australia as an illustration of how the shift to greater exchange rate flexibility and financial openness need not imply greater financial volatility if monetary policy is anchored in a credible and coherent operating strategy and if capital account convertibility is well sequenced and supported.
Stock market volatility, in and of itself, is neither good nor bad. As emphasised at the beginning of this paper, equity-price fluctuations convey signals that play an important role in resource allocation. But if equity markets are dominated by noise rather than signal, their volatility is less reassuring. This perspective suggests that it is important to limit the noise added by monetary policy and international transactions. Specifically, if the exchange rate anchor for monetary policy is cut adrift, it is important to put another anchor such as inflation targeting in its place. And, if the capital account is opened, it is important to put in place the institutional supports needed to ensure that capital account transactions are a stabilising force.
For the emerging markets that are following in the footsteps of the now-advanced economies, the implications are mixed. On the one hand, the historical decline in stock market volatility enjoyed by the advanced economies as their financial markets developed and matured suggests that emerging markets may similarly experience a decline in volatility as they graduate from the early stages of financial development. Insofar as volatility and crises go together – note that the concept of a crisis is sometimes operationalised as an extremity in the distribution of asset market returns (see, for example, Eichengreen, Rose and Wyplosz (1995)) – this change over time would suggest a tendency for the frequency of crises in emerging markets to decline to the lower levels characteristic of the now-advanced economies. On the other hand, the recent tendency for volatility to rise in the now-advanced economies suggests that there are also disturbing counter-currents – that something, be it changes in the monetary regime, the financial implications of globalisation or another factor, may be making for additional crisis risk. Unfortunately, the data for emerging markets do not speak clearly. The available time series are too short and buffeted by too many disturbances and structural breaks to allow us to conclude with any confidence that a similar u-shaped pattern is or will be evident there. This is a question that will have to be left for future historians.
Footnotes
The authors are George C Pardee and Helen N Pardee Professor of Economics and Political Science and Graduate Student in Economics, both at the University of California, Berkeley. This paper was prepared for the Reserve Bank of Australia's annual research conference on Asset Prices and Monetary Policy, Sydney, 18–19 August 2003. We are grateful to Andrew Rose, Michael Jansson, James Powell, Thomas Rothenberg and Adrian Pagan for helpful comments. [1]
The closest precedent for this observation of which we are aware is Catao and Timmerman (2003a, 2003b), who analyse monthly returns for firms from 13 countries from 1973 through 2002. Using switching regressions, they find that returns switch repeatedly from high-volatility to low-volatility states. That markets were in the high-volatility state at the end of the period is consistent with the existence of the right-hand arm of our intertemporal u, but the authors themselves (2003b, p 132) take the fact that volatility has shifted between the high- and low-volatility regimes repeatedly as ‘dispel[ling] the notion, held by some, that stock market volatility has been trending upward as financial markets become more globalised’. Their sample period is not long enough to determine whether the left-hand arm is present. [2]
We are tempted to say that this finding is contrary to the conventional wisdom, but it is not clear what the conventional wisdom is. Some will approach the question with the presumption that financial markets should have grown progressively more stable as market institutions and regulatory policies in the advanced countries have strengthened over time. Others, impressed by events like the LTCM crisis and the high-tech bubble, will question whether there has been any trend. Still others will presume the existence of an inverted u, dominated by high levels of volatility in the Great Depression of the 1930s. [3]
Here it is important to emphasise ‘some countries’. As we shall see, for a minority of countries in our sample, including Australia, financial internationalisation appears to be associated with less stock market volatility, not more. [4]
Suppose that the true standard deviation is not correlated over time – that is to say, that the past standard deviation cannot forecast the future standard deviation. Two consecutively estimated standard deviations from Officer's approach would still be highly correlated, since M–1 of the M observations used for estimating these two standard deviations are in common. [5]
We use the GARCH (1,1) model in what follows. Increasing the number of lags on the two terms changes none of our conclusions – either positive or negative. [6]
Analysing dollar returns for 20 emerging markets using data from the International Finance Corporation of the World Bank, the authors find that volatility is higher in emerging than mature markets (as much as five times higher) and that returns are more persistent. But in cases where α+β>=1, it is not clear how to interpret these results. Lumsdaine (1996) discusses the consistency and asymptotic normality of the quasi-maximum likelihood estimator when (α+β)=1 and finds that, in contrast to the case of a unit root in the conditional mean, the presence of a unit root in the conditional variance does not affect the limiting distribution of the estimators and that estimators are normally distributed. But this result is only for the simplest case where (α+β)=1 and no explanatory variables are included in the conditional variance equation. No result has been given for the case (α+β)>1. The current practice is to estimate α and β without restrictions and not to consider the implications for stationarity. For testing the null that α+β=1, Hong (1987) shows that traditional test procedures are still valid, so a Dickey-Fuller type of test for a unit root is not needed. [7]
Given that we have a nonlinear term in t, we must consider not only the consistency of the estimates (consistency
being an asymptotic property) but also how quickly they converge to the true
parameter values in finite samples. To obtain some intuition about this question
when there is no unit root, consider the case where 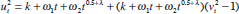 , and regard it as an OLS regression. When λ
∈ (0,0.5), the coefficients for t and t0.5+λ
will both be consistent in a sample of infinite size. The speed with which
the estimated value of ω2
converges to the true value is on the order of Tλ
(where T is the number of observations). Thus, as λ
goes up, the speed of convergence goes up as well; this makes it desirable
to work with relatively large values of λ. Unfortunately,
as λ
approaches 0.5, t0.5+λ
becomes close to t, and a problem of singularity is more likely
to arise (since t is also included in the regression). Experimenting
with different values of λ in the 0–0.5 range, we find
that singularity is still not severe when λ is as high as
0.45. Recall that the speed of convergence in the standard OLS regression
without non-stationary time series is on the order of T0.5.
Hence, the speed of convergence of the estimated value of ω2
with λ = 0.45 in a sample of 1,000 observations, which is
roughly what we have, is comparable to the speed of convergence of the standard
OLS regression without non-stationary time series in a sample of 500 observations.
In previous studies of historical financial market data, samples of 500 or
fewer observations are not uncommon. Thus, the estimates reported here converge
to the true values at least as quickly as in those studies. In practice,
it makes relatively little difference for the point estimates we obtain –
and for the u-shaped pattern in particular – what values of λ
we use. We thank Adrian Pagan for forcing us to think harder about the convergence
issue.
[8]
, and regard it as an OLS regression. When λ
∈ (0,0.5), the coefficients for t and t0.5+λ
will both be consistent in a sample of infinite size. The speed with which
the estimated value of ω2
converges to the true value is on the order of Tλ
(where T is the number of observations). Thus, as λ
goes up, the speed of convergence goes up as well; this makes it desirable
to work with relatively large values of λ. Unfortunately,
as λ
approaches 0.5, t0.5+λ
becomes close to t, and a problem of singularity is more likely
to arise (since t is also included in the regression). Experimenting
with different values of λ in the 0–0.5 range, we find
that singularity is still not severe when λ is as high as
0.45. Recall that the speed of convergence in the standard OLS regression
without non-stationary time series is on the order of T0.5.
Hence, the speed of convergence of the estimated value of ω2
with λ = 0.45 in a sample of 1,000 observations, which is
roughly what we have, is comparable to the speed of convergence of the standard
OLS regression without non-stationary time series in a sample of 500 observations.
In previous studies of historical financial market data, samples of 500 or
fewer observations are not uncommon. Thus, the estimates reported here converge
to the true values at least as quickly as in those studies. In practice,
it makes relatively little difference for the point estimates we obtain –
and for the u-shaped pattern in particular – what values of λ
we use. We thank Adrian Pagan for forcing us to think harder about the convergence
issue.
[8]
Daily indices for most of these countries are not available from GFD prior to the 1930s, although they could in principle be constructed from contemporary sources. In the 1920s, when interest in stock market indices grew, a number of these series were reconstructed back to the 1870s using procedures that are likely to create survivor bias. The other forms of survivor bias of concern to recent investigators are unlikely to be a problem here. For example, Goetzmann, Li and Rouwenhorst (2001) are concerned with the implications of the fact that firms disappear from market indices as they fail or are wound up. But since we wish to characterise market-wide returns made up of the returns to firms in the market at each point in time, we are not as concerned with this complication. [9]
For present purposes, it seems to make the most sense to express returns in different countries in a common unit (US dollars). In practice, this conversion does not affect our key results, as we explain below. [10]
Finland was also the first country that we considered in this research project. Research, like history, tends to display path dependence. [11]
We obtain virtually the same u-shape and very similar coefficients on ω1 and ω2 when we instead calculate the standard deviation of returns using 12 non-overlapping monthly returns (giving us 81 annual observations). The coefficient on ω1 is 0.016 with a p-value of 0.03, while the coefficient on ω2 is −1.5 with a p-value of 0.07. [12]
Below we find the same result for most of our other countries. Not surprisingly, other authors have found the same in analyses of shorter historical periods (over which the tendency for level reversion in the variance is presumably less). See Bollerslev, Chou and Kroner (1992) for discussion. [13]
Since the sample for Finland starts at March 1922, t11 will reach 279 at August 1945 and will stay at 279 till the end of the sample. t12 is equal to 0 until August 1945, and then takes on the value of t−279 thereafter. t13 is equal to t½ until August 1945. t13 reaches 16.7032 in August 1945, and stays at that value through the end of the sample. t14 is equal to 0 until the observation point August 1945, then it will be equal to t½−16.7032 thereafter. [14]
We use the standard OLS χ2 test as in Bollerslev, Engle and Nelson (1994), as suggested by the preceding discussion. [15]
Japan being the sole exception. [16]
The number of Splines differs across countries, as reflected in the number of estimated coefficients reported in the different columns of Table 3. [17]
For six countries, α+β is significantly less than 1 at the 1 per cent level. For these six cases, we say there is no unit root. For the others, we say that the unit root problem is not severe (in Table 5). [18]
In some cases, Canada for example, the casual reader may believe that two parabolas have been superimposed on the estimated conditional standard deviations. In fact, there is only one: the relatively flat u (whose coefficients are reported in Table 4). The other points are simply the estimated conditional standard deviations, which make up a cluster that resembles three parabolas when we estimate the GARCH (1,1) model with three Splines. Why is no mystery: the same parabolic shapes are vaguely evident in the left-hand panel, where standard deviations of stock returns are estimated using the nonparametric Officer method. [19]
We need to be careful in characterising the results for the early years in countries where there are data gaps at the beginning of the sample period. For example, the estimates for Switzerland suggest that the standard deviation increased in the early part of the sample period. Note, however, that the monthly stock market index only becomes available in 1916 (annual data begin in 1910). Thus, the timing for this country is somewhat different than the others. [20]
Finland is not included here because the relevant results already appear in Table 2. [21]
Note that the Spline function for Japan takes a special form: we fit a quadratic for the pre-1945 period but only the linear term for the second half of the sample. In other words, there is no coefficient for (t0.5 )2 in Table 3. That a special functional form is appropriate for Japan is not surprising; it was the one country for which there is no evidence of a unit root in the simple GARCH (1,1) model. [22]
Volatility estimates often get into trouble at the end of sample periods. Thus, some readers may worry that there is something spurious about the construction of our volatility estimates that produces high levels of volatility at the beginning and end of the sample. Note, however, that we have already eliminated the necessary lagged values at the beginning and end of the sample. If we eliminate more observations at the two sample ends, we are still unable to reject the null of a u-shaped pattern in Table 4 (since the coefficients there tend to be significantly different from zero at relatively high confidence levels). [23]
The main differences are that the coefficients for the u-shaped relationship estimated in Table 4 are no longer significant for Japan, and we obtain an inverted u for Canada. Note however that Canada was the country where evidence of the u-shaped pattern was statistically insignificant before. The implications of the conversion are less serious here than in, say, Goetzmann et al (2001), who are concerned with cross-market correlations. In that context, shocks to the value of the US dollar would affect the returns on every foreign market, expressed in US dollars, increasing the measured correlation. Here, in contrast, we analyse each country separately and are not concerned with cross-market correlations. [24]
Although they disagree in the extent of the output stabilisation; see Romer (1986) and Balke and Gordon (1989). [25]
Even if one is not convinced of our characterisation of volatility trends as u-shaped, the same implication follows from Catao and Timmerman's (2003a) conclusion that volatility levels have shifted repeatedly over time. [26]
In addition, authors like Campbell and Cochrane (1995) were led to explore the hypothesis that the additional volatility of the economy in certain periods can explain the rise in the conditional variance of returns when one allows for habit persistence in consumption. [27]
In effect, he argued for the existence of a ‘peso problem’. [28]
Bittlingmayer's (2002) analysis of stock market volatility in the Great Depression is consistent with this view; he constructs proxies for the probability of major changes in US policy (from a count of articles in the New York Times on anti-trust matters) and finds that this is strongly associated with stock market volatility. Voth (2002) constructs proxies for these probabilities in the 1920s and shows that they significantly explain stock market volatility. A related paper by Perotti and van Oijen (2001) also finds that political risk and stock market outcomes are correlated, but their study is not directly comparable in that it takes other stock market outcomes – market capitalisation, for example – as the dependent variable. [29]
In related work, Dellas and Hess (2002) analyse data for 47 countries and also find that stock market volatility is associated with output volatility, and that output volatility is associated in turn with exchange rate volatility – suggesting a role for the monetary regime. Similarly, Billio and Pelizzon (2002) find that the advent of the euro has reduced volatility in traditionally high-volatility European stock markets such as those of Spain and Italy. They also find that volatility has risen in Germany following the advent of the euro. This suggests that the new exchange rate regime may have implied a change in the actual or expected future policy regime (more stable for Italy and Spain, less stable for Germany). [30]
This is similar to the conclusion of Schwert (1989b), who finds that stock market volatility has fallen when the Fed has raised margin requirements, which is consistent with the notion that leverage is a source of volatility, working for example through the operation of positive feedback dynamics. [31]
It is, however, consistent with the finding in Bordo et al (2001) and Glick and Hutchison (2001) that currency crises – episodes of high asset market volatility and extreme realisations– are more prevalent in the presence of capital controls. [32]
Klein (2003) similarly identifies threshold effects for growth – per capita income levels only above which the effects of capital account liberalisation on growth are positive. [33]
Consistent with this, Claessens, Klingebiel and Schmukler (2002) find that the direct effect of capital account openness on market liquidity is positive, and that more market liquidity is generally associated with less market volatility. [34]
This has led various authors to further analyse market liquidity in order to gain insight into whether additional liquidity is likely to accentuate or diminish the volatility of financial markets. Claessens et al (2002) show that market liquidity is positively associated with incomes per capita (a general measure of the stage of economic development), the soundness of macroeconomic policies, more efficient legal systems with better shareholder protection, and a more open capital account. Other authors argue that more liquid markets tend to be more information efficient, suggesting that they may be more stable. Using data for the US, Lamoureux and Lastrapes (1990) show that trading volume, which they take as a proxy for information flow, significantly predicts future volatility. Dellas and Hess (2002) also find that the volatility of stock market returns declines with the development of a deeper and higher quality banking system. They argue that banks are important providers of both liquidity and information to stock markets. This is consistent with the view of Klein (2003) and Presad et al (2003) that financial integration will tend to reduce stock market volatility in countries with relatively well-developed financial systems and efficient information environments, but that it may have the opposite effect where these preconditions are absent. [35]
And because there are comparably long-time series on it for the subject countries, facilitating systematic analysis. In addition, many economists will find intuitively appealing the idea that the volatility of stock markets is connected, indeed causally, to the volatility of macroeconomic policies. In particular, those associated with the Reserve Bank of Australia will be tempted to ascribe the decline in stock market volatility in that country, which we document below, to the RBA's adoption of a more stable monetary policy framework (inflation targeting). We will have more to say about this later. [36]
See Bordo and Eichengreen (1999). At the same time, there is the counter-case of the 1930s, when financial globalisation declined sharply but stock market volatility rose. We will return to this as well in what follows. [37]
One could in principle add more explanatory variables (changes in domestic financial regulation, terms of trade shocks, fiscal disturbances); we leave this for future work. [38]
Requiring that we now drop New Zealand. [39]
Although we have monthly data for the US and the UK for all 12 decades and monthly series for the other countries for most of the post-World War II period, as described below. Measuring monetary policy using interest rates is even more problematic, since there do not exist consistent series for market-determined interest rates for all 12 sample countries. [40]
When monthly data become available, we re-calculate volatility on their basis. The results turn out to be very similar (see below). This reassures us that the monthly deviation estimated from the annual frequency is close to the monthly deviation estimated from the monthly frequency. [41]
Denmark being the exception. Note that we are regressing 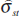 on a weighted average of lagged standard
deviations of the money supply growth rate (lagged one and two years). Timing
does not always provide identification, but these lags increase our confidence
that what we are picking up is causality running from monetary volatility
to stock market volatility rather than the other way around.
[42]
on a weighted average of lagged standard
deviations of the money supply growth rate (lagged one and two years). Timing
does not always provide identification, but these lags increase our confidence
that what we are picking up is causality running from monetary volatility
to stock market volatility rather than the other way around.
[42]
We will have more to say about this later. [43]
Monthly data and our methods indicate that the standard deviation of money supply growth fell from 1.33 in the period 1985–1989 to 1.20 in the period 1991–1995. Between the same periods the volatility of stock prices fell from 5.44 to 4.66. [44]
Another possibility is international financial liberalisation. We show momentarily that the removal of capital controls may have had a stabilising influence on financial markets in the Australian case. Here the timing is somewhat closer: Australia's controls were removed in 1983. [45]
Note that we are now forced to drop the US for lack of variation in the capital controls variable. [46]
Specifically, a number of recent authors have suggested that capital account openness is stabilising for domestic financial markets only when a country's institutional development and regulatory quality surpass a critical threshold (see e.g. Presad et al (2003)). That said, it is not clear how to interpret the constellation of coefficients estimated here. For example, it is not obviously the case that the effect of controls is different in countries with relatively well-developed financial markets: the coefficient on controls is negative for Switzerland but positive for the UK. It is not obvious that financial openness is associated with lower volatility in higher-income countries: controls are associated with additional volatility in France but less volatility in Japan. It is tempting to argue that capital account liberalisation is volatility-increasing in countries with bank-based financial systems and volatility-reducing in countries that rely on securitised finance, but France and, arguably, Australia fall into the wrong category. It could be that the effects are not constant over time, or that they are contingent on other factors, like the strength of domestic institutions and regulation, which is the direction in which the literature on the connections between international financial openness and economic growth has been heading in recent years. It is hard to say more at this point than that this complex relationship deserves further study. [47]
Levels of statistical significance are somewhat lower for a number of countries when we use monthly data for the shorter (post-World War II) period. [48]
The exceptions are Denmark and Japan. [49]
This reminds us that while monetary volatility may be associated with stock market volatility, both variables may in fact be reflecting the volatility of deeper determinants. [50]
The standard deviation of the money stock as we construct it becomes available for Finland only in 1916, so for that country we are unable to make the comparison. [51]
Which can be considered as largely predetermined over the long historical sweep. [52]
To be clear, we do not wish to draw implications from these results for the comparative merits of pegged and floating exchange rates. That would involve a larger calculation entailing much more than the implications for stock market volatility (which are, as we have seen, contingent in any case). [53]
References
Balke N and R Gordon (1989), ‘The estimation of prewar GNP: methodology and new results’, Journal of Political Economy, 97(1), pp 38–92.
Bekaert G and CR Harvey (1997), ‘Emerging equity market volatility’, Journal of Financial Economics, 43(1), pp 29–77.
Billio M and L Pelizzon (2002), ‘The European single currency and the volatility of European stock markets’, University of Venice and University of Padua, unpublished manuscript.
Binder J and M Merges (2001), ‘Stock market volatility and economic factors’, Review of Quantitative Finance and Accounting, 17(1), pp 5–26.
Bittlingmayer G (2002), ‘The 1920's boom, the great crash, and after’, University of Kansas, unpublished manuscript.
Bollerslev T (1986), ‘Generalized autoregressive conditional heteroskedasticity’, Journal of Econometrics, 31(3), pp 307–327.
Bollerslev T, R Chou and K Kroner (1992), ‘ARCH modeling in finance: a review of the theory and empirical evidence’, Journal of Econometrics, 52, pp 5–59.
Bollerslev T, RF Engle and DB Nelson (1994), ‘ARCH models’, Handbook of econometrics, 4, North Holland, Amsterdam, pp 2961–3038.
Bordo M and B Eichengreen (1999), ‘Is our current international economic environment unusually crisis prone?’, in D Gruen and L Gower (eds), Capital flows and the international financial system, Proceedings of a Conference, Reserve Bank of Australia, Sydney, pp 18–74.
Bordo M, B Eichengreen, D Klingebiel and MS Martinez-Peria (2001), ‘Is the crisis problem growing more severe?’, Economic Policy, 32, pp 53–82.
Calvo G and E Mendoza (2000), ‘Rational contagion and the globalization of securities markets’, Journal of International Economics, 51(1), pp 79–113.
Campbell J and J Cochrane (1995), ‘By force of habit: a consumption-based explanation of aggregate stock market behavior’, NBER Working Paper No 4995.
Capie F and G Wood (1985), A monetary history of the United Kingdom, 1870–1982, Allen & Unwin, London.
Catao L and A Timmerman (2003a), ‘Country and industry dynamics in stock returns’, IMF Working Paper WP/03/52.
Catao L and A Timmerman (2003b), ‘Deciphering the determinants of stock market volatility’, IMF Survey, 32, pp 132–134.
Claessens S, D Klingebiel and S Schmukler (2002), ‘Explaining the migration of stocks from exchanges in emerging economies to international centers’, University of Amsterdam and World Bank, unpublished manuscript.
Dellas H and M Hess (2002), ‘Financial development and stock returns: a cross-country analysis’, Center for Economic Policy Research Discussion Paper Series No 3681.
DeLong JB (1996), ‘America's only peacetime inflation: the 1970s’, NBER Historical Paper No 84.
Eichengreen B, A Rose and C Wyplosz (1995), ‘Exchange market mayhem: the antecedents and aftermath of speculative attacks’, Economic Policy: A European Forum, 21, pp 251–312.
Errunza V and K Hogan (1995), ‘Macroeconomic determinants of European stock market volatility’, Barclays Global Investors, unpublished manuscript.
Friedman M and A Schwartz (1963), A monetary history of the United States 1867–1960, National Bureau of Economic Research Studies in Business Cycles No 12, Princeton University Press, Princeton.
Glick R and M Hutchison (2001), ‘Stopping “hot money” or signaling bad policy? Capital controls in the onset of currency crises’, Federal Reserve Bank of San Francisco and University of California, Santa Cruz, unpublished manuscript.
Goetzmann WN, L Li and KG Rouwenhorst (2001), ‘Long-term global market correlations’, NBER Working Paper No 8612.
Hong CH (1987), ‘The integrated generalized autoregressive conditional heteroskedasticity model: the process, estimation and some Monte Carlo experiments’, University of California, San Diego, unpublished manuscript.
IMF (International Monetary Fund) (2003), Global financial stability review, Washington DC.
Jorion P and W Goetzmann (1999), ‘Global stock markets in the twentieth century’, Journal of Finance, 54(3), pp 953–980.
Klein M (2003), ‘Capital account openness and the varieties of growth experience’, NBER Working Paper No 9500.
Kose MA, ES Prasad and ME Terrones (2003), ‘Financial integration and macroeconomic volatility’, IMF Working Paper No WP/03/50.
Lamoureux CG and WD Lastrapes (1990), ‘Heteroskedasticity in stock return data: volume versus GARCH effects’, Journal of Finance, 45(1), pp 221–229.
Lee SW and B Hansen (1994), ‘Asymptotic theory for the GARCH(1,1) quasi-maximum likelihood estimator’, Econometric Theory, 10(1), 29–52.
Lumsdaine RL (1996), ‘Consistency and asymptotic normality of the quasi-maximum likelihood estimator in IGARCH(1,1) and covariance stationary GARCH(1,1) models’, Econometrica, 64(3), pp 575–596.
Officer R (1973), ‘The variability of the market factor of the New York Stock Exchange’, Journal of Business, 46(3), pp 434–453.
Perotti E and P van Oijen (2001), ‘Privatization, political risk and stock market development in emerging economies’, Journal of International Money and Finance, 20(1), pp 43–69.
Presad E, K Rogoff, S Wei, and MA Kose (2003), ‘Effects of financial globalization on developing countries: some empirical evidence’, manuscript available at <http://www.imf.org/external/np/res/docs/2003/031703.htm>.
Romer CD (1986), ‘Is the stabilization of the postwar economy a figment of the data?’, American Economic Review, 76(3), pp 314–334.
Sargent T (1999), The conquest of American inflation, Princeton University Press, Princeton.
Schwert GW (1989a), ‘Business cycles, financial crises and stock volatility’, NBER Working Paper No 2957.
Schwert GW (1989b), ‘Why does stock market volatility change over time?’, Journal of Finance, 44(5), pp 1115–1153.
Voth H (2002), ‘Why was stock market volatility so high during the Great Depression? Evidence from 10 countries during the interwar period’, Centre for Economic Policy Research Discussion Paper Series No 3254.