RBA Annual Conference – 2003 Home-buyers, Housing and the Macroeconomy Karl E Case, John M Quigley and Robert J Shiller[1]
Abstract
We present the results of a new survey of US home-buyers in 2002. The most important finding is that the survey suggests that home-buyers' expectations are substantially affected by recent experience. Even after a long boom that has taken prices to very high levels, home-buyers typically have expectations that prices will show double-digit annual price growth over the next 10 years, apparently with only a modest level of risk. We conjecture that these characteristics of individuals' expectations may contribute to the substantial swings that are observed in housing prices. Changes in housing wealth, especially if they are perceived as long-lasting, may have substantial macroeconomic effects through private consumption. In the second part of the paper, we examine the link between increases in housing wealth, financial wealth, and consumer spending. We rely upon a panel of 14 countries observed annually for various periods during the past 25 years and a panel of US states observed quarterly during the 1980s and 1990s. We find a statistically significant and rather large effect of housing wealth upon household consumption.
1. Introduction
Since 1995 housing prices in virtually every metropolitan area in the US have been rising faster than incomes and faster than other prices. Despite the fact that the economy was in recession during the first three quarters of 2001 and despite the loss of nearly 3 million jobs, the price of single-family homes, the volume of existing home sales and the number of housing starts in the US have remained at near-record levels. There can be no doubt that the housing market and spending related to housing sales have kept the US economy growing and has prevented a ‘double dip’ recession since 2001.
However, the historical record provides reasons for concern over the substantial price growth that has occurred in recent years. During the 1980s, spectacular home-price booms in California and the Northeast helped stimulate the underlying economy on the way up, but they ultimately encountered a substantial drop in demand in the late 1980s and contributed significantly to severe regional recessions in the early 1990s. Indeed, in the current episode, the housing market is also beginning to show signs of cooling. Inventories and vacancy rates are rising, and volume numbers are showing signs of a potential turnaround. The popular press is full of speculation that the housing bubble is about to burst. Barrons, Money Magazine and The Economist have all run recent feature stories about the potential for a crash in home prices.
This pattern of strength in housing prices amid weakness in equity prices has also been seen in many other countries. These developments have sparked further interest in understanding the effect of different components of household wealth, not merely stock market or financial wealth, upon consumption levels. Indeed, there is every reason to expect that changes in housing wealth exert effects upon household behaviour that are similar in nature (if not in size) to those hypothesised for the stock market, especially given that institutional innovations (such as second mortgages in the form of secured lines of credit) have made it as simple to extract cash from housing equity as it is to sell shares or borrow on margin.[2] However, there has been virtually no comparative research on this issue, which suggests it may be worthwhile to test whether the tendency to consume out of stock market wealth is different from the tendency to consume out of housing wealth.
This paper addresses two major issues. First, we explore the dynamics of home prices between 1982 and 2003. We begin by reviewing our own work on the cycles of the late 1980s in which we found substantial evidence of inertia and speculative behaviour. We then analyse state-level data on home prices and incomes over a period of 71 quarters. Finally, we will present the results of a survey of home-buyers in 2002. The survey replicates one done in 1988 in four metropolitan areas: Orange County (California), San Francisco, Boston and Milwaukee. The goal is to shed light on the nature of the recent boom, the extent of speculative behaviour on the part of home-buyers and the potential for a near-term collapse. The results from this section suggest that household attitudes and behaviour might have speculative elements that contribute to the price dynamics in the housing market and thereby have important effects on the macroeconomy.
The second part of the paper provides empirical evidence on the relationship between house and stock prices and private consumption. We rely on two bodies of data: a panel of annual observations on 14 countries, measuring aggregate consumption, the capitalisation of stock market wealth, and aggregate housing wealth; and an analogous panel of quarterly observations on US states, estimating consumption, stock ownership, and aggregate housing wealth. These data exploit variations in the geographical distribution of stock market and housing market wealth among the US states and the substantial variations in the timing and intensity of economic activity across developed countries. Our time-series cross-section method is eclectic; we present analyses in levels, first differences, and in error-correction-model (ECM) forms, and with alternative assumptions about error terms and fixed effects.
Section 2 below discusses the results of our survey of home-buyer attitudes and behaviour, along with some empirical analysis of house prices in different US states. Section 3 provides a brief theoretical motivation for the distinction between housing and financial wealth and a review of the limited evidence on the effects of housing wealth on consumption and savings behaviour. Section 4 describes the data sources, imputations, and the computations used to create the two panels. Section 5 presents our statistical results. Section 6 is a brief conclusion.
2. A Comparison of the Current and Previous US Housing Booms
2.1 The 1980s booms
Housing prices began rising rapidly in Boston in 1984. In 1985 alone house prices in the Boston metropolitan area went up 39 per cent. In Case (1986), repeat sales indices were constructed to measure the extent of the boom in constant quality home prices. In addition, a structural supply and demand model, which explained house price movements over 10 years and across 10 cities, failed to explain what was going on in Boston. The model predicted that income growth, employment growth, interest rates, construction costs and other fundamentals should have pushed Boston prices up by about 15 per cent. Instead, they went up over 140 per cent before topping out in 1988. The paper ends with the conjecture that the boom was at least in part a bubble.
Case and Shiller (1987) described price changes by constructing a set of repeat sales indices from large databases of transactions in Atlanta, Chicago, Dallas and San Francisco. These indices were used in Case and Shiller (1989) to provide evidence of positive serial correlation in real house prices. In fact, the paper showed that a change in price observed over one year tends to be followed by a change in the same direction the following year between 25 per cent and 50 per cent as large. The paper finds evidence of inertia in excess returns as well.
Case and Shiller (1988) present the results of a survey of a sample of around 2,000 households that bought homes in May 1988 in four markets: Orange County (California), San Francisco, Boston, and Milwaukee. The four cities were chosen to represent hot (California), cold (Boston) and steady (Milwaukee) markets. The survey was inspired by an article on page one of the June 1, 1988 Wall Street Journal, which described the current ‘frenzy in California's big single family home market’. The results provide strong evidence that buyers are influenced by an investment motive, that they have strong expectations about future price changes in their housing markets, and that they perceive little risk. Responses to a number of questions revealed that emotion plays a significant role in house purchase decisions. In addition, there was no agreement among buyers about the causes of recent house price movements.
One additional finding in Case and Shiller (1988) lends support to an important stylised fact about the US housing market that has not been well documented in the literature, which is that house prices are sticky downward. That is, when excess supply occurs, prices do not immediately fall to clear the market. Rather, sellers have reservation prices below which they tend not to sell.
Finally, Case and Shiller (1990) use time-series cross-section regressions to test for the forecastability of prices and excess returns using a number of independent variables. The paper finds that the ratio of construction costs to price, changes in the adult population, and increases in real per capita income are all positively related to house prices and excess returns. The results add weight to the argument that the market for single-family homes is inefficient.
2.2 House prices and income 1985–2002
One question that seems never to have been explored in the literature is the stability of the relationship between income and house prices over time and space. If that relationship is stable, then clearly fundamentals explain house prices. This section looks at the relationship between house price and per capita personal income by state quarterly from 1985:Q1 to 2002:Q3. In all (50 states and the District of Columbia and 71 quarters) the data contain 3,621 observations.
Our data for home prices were constructed from repeat sales price indices applied to the 2000 Census median values by state. Case-Shiller weighted repeat sales indices (see Case and Shiller (1987, 1989)) constructed by Fiserv Case Shiller Weiss, Inc. are available for 16 states and were used where available. For other states we use state-level repeat value indices produced by Fannie Mae and Freddie Mac.[3] The baseline figures for state level mean home prices are based on owner estimates in the 2000 Census. The panel on home prices was constructed as follows for each state:

where
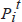 = adjusted median home value in state i
at time t,
= adjusted median home value in state i
at time t,
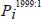 = mean value of owner-occupied homes in state
i in 1999:Q1, and
= mean value of owner-occupied homes in state
i in 1999:Q1, and
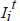 = weighted repeat sales price index for state
i, 1999:Q1 = 1.
= weighted repeat sales price index for state
i, 1999:Q1 = 1.
Our data for per capita personal income are based on data for personal income by state from the Bureau of Economic Analysis. It is a consistent time series produced on a timely schedule. However, population figures by state are not easy to obtain quarterly and the most carefully constructed series that we could find was put together by Economy.com, formerly Regional Financial Associates.
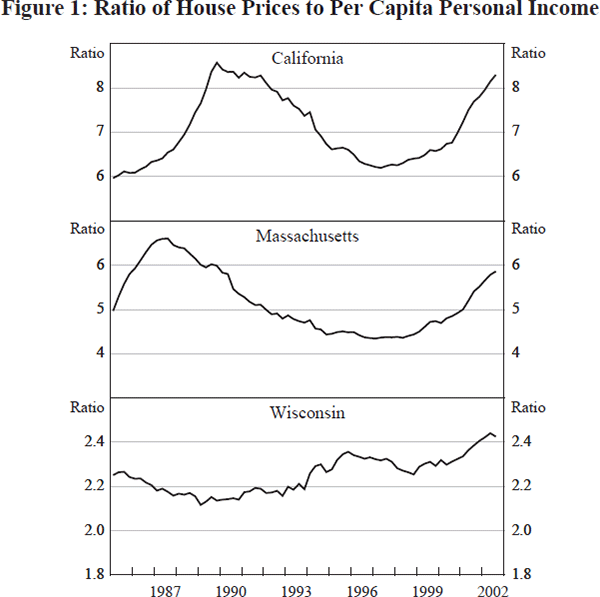
Table 1 presents the ratio of house price to per capita income for the eight most volatile states and the seven least volatile states. The least volatile states exhibit remarkable stability and very low ratios. Wisconsin, for example, a state that we will explore at some length later, has a ratio that remains between 2.1 and 2.4 for the entire 18 years. A simple regression of house price on per capita income in Wisconsin generates an R2 of 0.99.
| State | Min | Max | Std dev | 2002:Q3 | Quarter of peak | R2(a) |
|---|---|---|---|---|---|---|
| Hawaii | 7.8 | 12.5 | 1.30 | 10.1 | 1992:Q3 | 0.83 |
| Connecticut | 4.5 | 7.8 | 1.10 | 5.4 | 1988:Q1 | 0.45 |
| New Hampshire | 4.0 | 6.6 | 0.84 | 5.3 | 1987:Q2 | 0.49 |
| California | 6.0 | 8.6 | 0.80 | 8.3 | 1989:Q4 | 0.78 |
| Rhode Island | 4.6 | 7.1 | 0.75 | 6.1 | 1988:Q1 | 0.65 |
| Massachusetts | 4.3 | 6.6 | 0.71 | 5.9 | 1987:Q3 | 0.70 |
| New Jersey | 4.5 | 6.8 | 0.67 | 5.6 | 1987:Q3 | 0.73 |
| New York | 3.8 | 5.6 | 0.51 | 4.9 | 1987:Q3 | 0.77 |
| Nebraska | 1.8 | 2.1 | 0.09 | 1.9 | 1985:Q2 | 0.96 |
| Wisconsin | 2.1 | 2.4 | 0.08 | 2.4 | 2002:Q3 | 0.99 |
| Illinois | 2.6 | 2.9 | 0.08 | 2.9 | 2002:Q3 | 0.98 |
| Kentucky | 2.1 | 2.4 | 0.07 | 2.2 | 1985:Q1 | 0.99 |
| Indiana | 2.0 | 2.3 | 0.06 | 2.1 | 1986:Q4 | 0.99 |
| Iowa | 1.7 | 1.9 | 0.06 | 1.8 | 2002:Q3 | 0.98 |
| Ohio | 2.3 | 2.5 | 0.04 | 2.5 | 2002:Q3 | 0.99 |
| (a) R2 from a regression of Ln(house price) on Ln(per capital income), 71 observations. | ||||||
On the other hand, the eight most volatile states exhibit equally remarkable instability. Connecticut, for example, has a ratio that varies between 4.5 and 7.8, and we find that income only explains 45 per cent of the variation in house price. Table 2 shows the variation for all 50 states and the District of Columbia (DC). Glancing down the table reveals that 43 of the 51 observations have a standard deviation at or below 0.41, while only those eight described in Table 1 are above 0.41. These calculations reveal that states seem to fall into one of two categories. For the vast majority of states, prices seem to move very much in line with income. But in New England, New York, New Jersey, California and Hawaii, prices seem to be significantly more volatile.
| State | Median | Min | Max | Std dev | Mean |
|---|---|---|---|---|---|
| Hawaii | 9.79 | 7.83 | 12.50 | 1.34 | 10.03 |
| Connecticut | 5.41 | 4.47 | 7.84 | 1.06 | 5.67 |
| New Hampshire | 4.68 | 3.98 | 6.63 | 0.84 | 4.94 |
| California | 6.76 | 5.96 | 8.57 | 0.80 | 7.07 |
| Rhode Island | 5.49 | 4.58 | 7.12 | 0.75 | 5.62 |
| Massachusetts | 4.97 | 4.34 | 6.60 | 0.72 | 5.20 |
| New Jersey | 5.25 | 4.48 | 6.77 | 0.68 | 5.34 |
| New York | 4.54 | 3.83 | 5.60 | 0.52 | 4.55 |
| Texas | 2.48 | 2.20 | 3.59 | 0.41 | 2.61 |
| Maine | 3.98 | 3.44 | 4.77 | 0.40 | 3.98 |
| DC | 3.61 | 3.10 | 4.52 | 0.37 | 3.66 |
| Vermont | 4.11 | 3.64 | 4.85 | 0.37 | 4.19 |
| Louisiana | 2.56 | 2.42 | 3.53 | 0.33 | 2.70 |
| Alaska | 3.26 | 2.48 | 4.07 | 0.33 | 3.29 |
| Oregon | 2.25 | 1.49 | 2.69 | 0.32 | 2.23 |
| Utah | 2.87 | 2.29 | 3.21 | 0.31 | 2.81 |
| Mississippi | 2.28 | 2.21 | 3.15 | 0.29 | 2.43 |
| Maryland | 4.01 | 3.62 | 4.69 | 0.29 | 4.05 |
| Oklahoma | 2.13 | 2.05 | 3.04 | 0.28 | 2.25 |
| Washington | 3.12 | 2.28 | 3.36 | 0.26 | 3.00 |
| Delaware | 3.62 | 3.33 | 4.14 | 0.26 | 3.69 |
| Colorado | 2.60 | 2.19 | 3.18 | 0.25 | 2.57 |
| Virginia | 3.47 | 3.04 | 3.87 | 0.24 | 3.44 |
| Georgia | 2.76 | 2.58 | 3.25 | 0.23 | 2.83 |
| Arizona | 3.53 | 3.38 | 4.17 | 0.22 | 3.63 |
| North Dakota | 2.24 | 2.05 | 2.98 | 0.22 | 2.32 |
| Arkansas | 2.22 | 2.13 | 2.84 | 0.22 | 2.33 |
| Montana | 2.55 | 2.02 | 2.71 | 0.22 | 2.44 |
| Florida | 3.04 | 2.80 | 3.51 | 0.21 | 3.08 |
| Missouri | 2.32 | 1.18 | 2.71 | 0.21 | 2.38 |
| Pennsylvania | 2.70 | 2.43 | 3.14 | 0.21 | 2.73 |
| Wyoming | 2.12 | 1.82 | 2.65 | 0.21 | 2.15 |
| New Mexico | 3.38 | 3.12 | 3.85 | 0.20 | 3.40 |
| Tennessee | 2.35 | 2.23 | 2.80 | 0.19 | 2.43 |
| Nevada | 3.56 | 3.32 | 3.97 | 0.18 | 3.59 |
| Alabama | 2.38 | 2.31 | 2.84 | 0.17 | 2.47 |
| Michigan | 1.93 | 1.69 | 2.37 | 0.17 | 1.98 |
| Minnesota | 2.40 | 2.27 | 2.92 | 0.16 | 2.47 |
| North Carolina | 2.60 | 2.50 | 2.98 | 0.16 | 2.67 |
| Idaho | 2.58 | 2.27 | 2.91 | 0.15 | 2.58 |
| West Virginia | 2.32 | 2.22 | 2.79 | 0.15 | 2.38 |
| South Carolina | 2.69 | 2.57 | 3.06 | 0.15 | 2.74 |
| Kansas | 1.97 | 1.84 | 2.30 | 0.14 | 2.02 |
| South Dakota | 1.87 | 1.73 | 2.20 | 0.11 | 1.89 |
| Nebraska | 1.88 | 1.76 | 2.12 | 0.09 | 1.89 |
| Illinois | 2.74 | 2.57 | 2.87 | 0.08 | 2.73 |
| Wisconsin | 2.26 | 2.12 | 2.44 | 0.08 | 2.25 |
| Kentucky | 2.21 | 2.11 | 2.41 | 0.08 | 2.23 |
| Iowa | 1.78 | 1.68 | 1.92 | 0.06 | 1.79 |
| Indiana | 2.12 | 2.03 | 2.25 | 0.06 | 2.13 |
| Ohio | 2.34 | 2.27 | 2.46 | 0.04 | 2.34 |
Plots of the ratio of price to per capita income for the states of California, Massachusetts and Wisconsin (Figure 1) show clearly that the pattern of variation is anything but a random walk in California and Massachusetts. In these states the pattern is long inertial upswings followed by long inertial downturns followed by another rise that has lasted several years. In Wisconsin, the ratio is much smaller and remarkably stable.
2.3 Home-buyer behaviour: 1988 and 2002
These patterns are a backdrop for our survey results. Earlier we described the results of a survey of home-buyers done in 1988 in four metropolitan areas: Orange County (California), San Francisco, Boston and Milwaukee. We turn now to some new results, from a replication of that survey done for home-buyers in mid 2002.
Our 2002 survey was sent to 2,000 persons who bought homes between March and August of 2002. A random sample of 500 sales was drawn from each of four counties: Orange County, California; Alameda County (San Francisco), California; Middlesex County (Boston), Massachusetts; and Milwaukee County, Wisconsin. Just under 700 surveys were returned completed and usable this time; the response rate was somewhat higher for the 1988 survey. Response rates for each county are given in Table 3. The questionnaire was 10-pages long and included questions on a number of topics. The focus was on the home-buyers' expectations and behaviour. During the first cycle of surveys, we had two markets booming (the California counties), one market at its peak and showing excess supply (Boston) and one drifting market (Milwaukee). This time we got all four markets at recent highs, but with the economy in recession or slowly coming out of recession. In addition, this time the Fed had lowered interest rates to historic lows at the time these buyers were signing purchase and sale agreements. In 1988, interest rates were on the rise.
| City/Metropolitan area | Sample | Returns tabulated | Response rate Per cent | |||||
|---|---|---|---|---|---|---|---|---|
| 1988 | 2002 | 1988 | 2002 | 1988 | 2002 | |||
| Orange County | 500 | 500 | 241 | 143 | 48.2 | 28.6 | ||
| San Francisco | 530 | 500 | 199 | 164 | 37.5 | 32.8 | ||
| Boston | 500 | 500 | 200 | 203 | 40.0 | 40.6 | ||
| Milwaukee | 500 | 500 | 246 | 187 | 49.2 | 37.4 | ||
| All regions | 2,030 | 2,000 | 886 | 697 | 43.9 | 34.9 | ||
Table 4 describes the sample. A substantial majority of buyers were buying a primary residence, and only a small minority were buying to rent. First-time buyers were a majority of the sample in Milwaukee. The lowest percentage of first-time buyers was in Orange County. We were surprised to see that more than 90 per cent of respondents to the 2002 survey in all four markets were buying single-family houses, whereas this proportion was a significantly smaller portion in the 1988 survey. We have no explanation as yet for this.
| Description | Orange County | San Francisco | Boston | Milwaukee | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1988 | 2002 | 1988 | 2002 | 1988 | 2002 | 1988 | 2002 | ||||
| Single-family home | 70.0 | 95.2 | 55.9 | 96.4 | 39.7 | 97.5 | 71.1 | 91.6 | |||
| First-time purchase | 35.8 | 31.7 | 36.2 | 46.0 | 51.5 | 41.6 | 56.9 | 53.1 | |||
| Bought to live in as a primary residence |
88.4 | 95.6 | 72.7 | 93.3 | 92.0 | 97.1 | 88.2 | 90.0 | |||
| Bought to rent to others | 3.7 | 2.8 | 12.1 | 3.0 | 3.0 | 0.9 | 4.1 | 5.3 | |||
Although the timing of their cycles has not been identical, Orange County, San Francisco and Boston have experienced two boom cycles and a bust over the last 20 years. Table 5 describes the timing and the extent of these cycles which are also shown in Figure 2. The first booms in California were similar in Los Angeles and San Francisco. Both metropolitan areas peaked in the second quarter of 1990 after a 125 per cent run-up which began slowly, gradually accelerating into 1988 and then slowing as it approached the peak. The first boom in Boston was similar but it accelerated earlier and actually peaked in the third quarter of 1988 after a 143 per cent increase. The bust that followed was most severe and long-lived in Los Angeles, which dropped 29 per cent from the peak to a trough in the first quarter of 1996. San Francisco only dropped 14 per cent and began rising again in the first quarter of 1993, three years earlier. Boston was on the mend even two years earlier than that. All three metropolitan areas have seen a prolonged boom period ever since, although San Francisco has shown some volatility since mid 2002. Home prices during this boom rose 129 per cent in San Francisco, 94 per cent in Los Angeles and 126 per cent in Boston. At the time that respondents to the second survey were buying their homes, prices were still rising in all four metropolitan areas.
| Los Angeles | San Francisco | Boston | Milwaukee | |
|---|---|---|---|---|
| 1982–peak | +128% | +126% | +143% | – |
| Peak quarter | 1990:Q2 | 1990:Q2 | 1988:Q3 | |
| Peak to trough | −29% | −14% | −16% | – |
| Trough quarter | 1996:Q1 | 1993:Q1 | 1991:Q1 | |
| Trough to peak | +94% | +129% | +126% | – |
| Peak quarter | 2003:Q1 | 2002:Q3 | 2003:Q1 | |
| 1982:Q1–2003:Q1 | +214% | +325% | +419% | +213% |
| Average, annual rate | 5.6% | 7.1% | 8.2% | 5.6% |
|
Source: Fiserv Case Shiller Weiss, Inc., repeat sales indexes |
||||
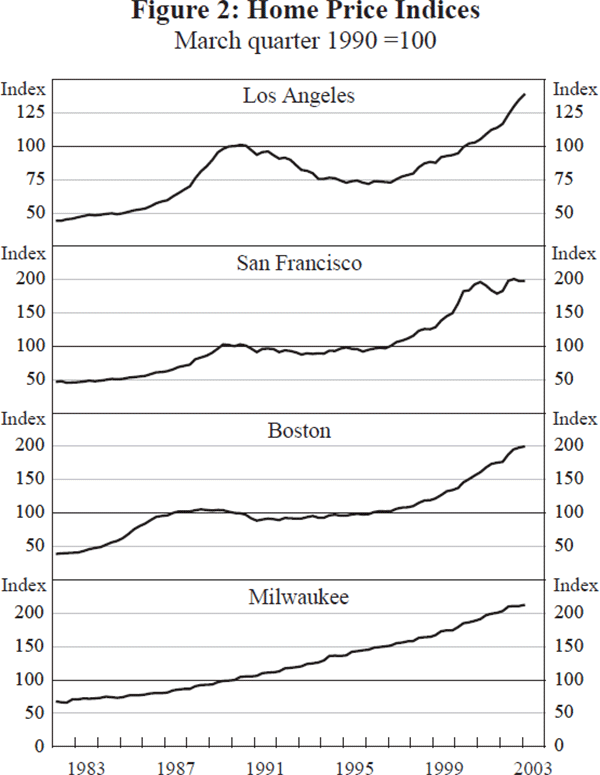
The price index for Milwaukee could not be more different. It shows a very steady climb at a rate of 5.6 per cent annually, essentially the same rate of growth as per capita income. Interestingly, over the entire cycle, Milwaukee did about as well as Los Angeles, but not as well as Boston. Over the entire cycle, house prices in Boston increased more than five-fold, while prices in San Francisco quadrupled and prices in both Milwaukee and Los Angeles tripled.
Table 6 looks at the latest boom cycle in a bit more detail. Using the state data described above, the table makes two points. First, in all three states, home price increases outpaced income growth. Note that the price increases were not as great as in the metropolitan area data because the indices were for the entire state. All three states had increases in their ratios of home price to income, but the changes were dramatically larger in the boom-bust states. Second, we note that the decline in interest rates this cycle from 8.8 per cent (30-year fixed) in 1995 to 6 per cent at the time the sample was drawn kept the monthly payment required to buy the median home from rising. It actually fell in California and Wisconsin.
| California | Massachusetts | Wisconsin | |
|---|---|---|---|
| House price 1995:Q1 | 158,954 | 121,091 | 50,557 |
| House price 2002:Q3 | 276,695 | 231,994 | 73,071 |
| Total change | +74% | +92% | +45% |
| Annual rate | 7.7% | 9.1% | 5.1% |
| Personal income/pop 1995:Q1 | 24,044 | 27,224 | 22,203 |
| Personal income/pop 2002:Q3 | 33,362 | 39,605 | 30,138 |
| Total change | +39% | +45% | +35% |
| Annual rate | 4.5% | 5.1% | 4.1% |
| House price/income 1995:Q1 | 6.61 | 4.45 | 2.28 |
| House price/income 2002:Q3 | 8.29 | 5.86 | 2.42 |
| Annual mortgage payment 1995:Q1 | 12,145 | 9,253 | 3,862 |
| Annual mortgage payment 2002:Q3 | 15,908 | 13,338 | 4,201 |
| Payment/income 1995:Q1(a) | 0.51 | 0.34 | 0.17 |
| Payment/income 2002:Q3(a) | 0.47 | 0.34 | 0.14 |
|
(a) Annual mortgage payment assumes 80% LTV, 30-year fixed rate; February 1995: 8.8%, August 2002: 6.0% (sourced from Fannie Mae). Sources: State personal income – US Department of Commerce, Bureau of Economic Analysis; state population – Regional Financial Associates (Economy.com); house price – 1989 median, US Census adjusted using Case Shiller Weiss or blended repeat sales price index |
|||
2.4 Attitudes to housing as an investment
Table 7 presents the responses to questions about housing as an investment. For the vast majority of buyers, investment was ‘a major consideration’ or they at least ‘in part’ thought of it as an investment. Interestingly, a slightly smaller percentage in 2002 cited investment as a factor on the coasts than was the case in 1988. In Milwaukee and San Francisco it was a major consideration for a majority of buyers.
| Question | Orange County | San Francisco | Boston | Milwaukee | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1988 | 2002 | 1988 | 2002 | 1988 | 2002 | 1988 | 2002 | ||||
| ‘In deciding to buy your property, did you think of the purchase as an investment?’ |
(N=238) | (N=143) | (N=199) | (N=164) | (N=200) | (N=203) | (N=243) | (N=187) | |||
| ‘It was a major consideration’ | 56.3 | 46.8 | 63.8 | 51.8 | 48.0 | 33.9 | 44.0 | 50.3 | |||
| ‘In part’ | 40.3 | 46.2 | 31.7 | 34.4 | 45.0 | 56.2 | 45.7 | 42.2 | |||
| ‘Not at all’ | 4.2 | 7.0 | 4.5 | 9.8 | 7.0 | 9.9 | 10.3 | 7.5 | |||
| ‘Why did you buy the home that you did?’ | (N=238) | (N=143) | (N=199) | (N=164) | (N=199) | (N=203) | (N=246) | (N=187) | |||
| ‘Strictly for investment purposes’ | 19.8 | 7.5 | 37.2 | 10.6 | 15.6 | 8.2 | 18.7 | 13.8 | |||
| ‘Buying a home in _____ today involves:’ | (N=237) | (N=143) | (N=192) | (N=164) | (N=197) | (N=203) | (N=237) | (N=187) | |||
| ‘A great deal of risk’ | 3.4 | 7.9 | 4.2 | 14.8 | 5.1 | 7.8 | 5.9 | 4.3 | |||
| ‘Some risk’ | 33.3 | 47.5 | 40.1 | 51.9 | 57.9 | 62.5 | 64.6 | 57.3 | |||
| ‘Little or no risk’ | 63.3 | 44.6 | 55.7 | 33.3 | 37.1 | 29.6 | 29.5 | 38.4 | |||
Similarly, only a small percentage of buyers thought that housing involved a great deal of risk in all cities, although the figure was not surprisingly highest in San Francisco in 2002. By and large there was more perception of risk on the coasts in 2002 than in 1988, but less perception of risk in Milwaukee. In all four counties, people were less likely to be buying a home ‘strictly for investment purposes’ in 2002. The decline was particularly sharp for California.
Table 8 presents the responses to three questions that we did not ask in 1988. There has been a lot of discussion about people shifting their assets toward housing because the stock market has done so poorly since 2000. However, a falling stock market could have a negative wealth effect on home-buying decisions. Note that the survey was completed well before the stock market rally of 2003.
| Question | Orange County | San Francisco | Boston | Milwaukee |
|---|---|---|---|---|
| ‘Do you agree with the following statement: “Real estate is the best investment for long-term holders, who can just buy and hold through the ups and downs of the market”?’ |
(N=145) | (N=162) | (N=204) | (N=185) |
| ‘Strongly agree’ | 53.7 | 50.6 | 36.7 | 31.3 |
| ‘Somewhat agree’ | 33.1 | 39.5 | 48.5 | 45.9 |
| ‘Neutral’ | 10.3 | 6.7 | 9.3 | 11.3 |
| ‘Somewhat disagree’ | 2.7 | 2.4 | 4.9 | 9.1 |
| ‘Strongly disagree’ | 0.0 | 0.6 | 0.4 | 2.1 |
| ‘Do you agree with the following statement: “The stock market is the best investment for long-term holders, who can just buy and hold through the ups and downs of the market”?’ | (N=145) | (N=162) | (N=203) | (N=187) |
| ‘Strongly agree’ | 8.2 | 8.0 | 14.7 | 14.9 |
| ‘Somewhat agree’ | 32.4 | 38.2 | 44.3 | 33.6 |
| ‘Neutral’ | 32.4 | 27.7 | 17.7 | 25.6 |
| ‘Somewhat disagree’ | 20.0 | 16.0 | 15.2 | 20.3 |
| ‘Strongly disagree’ | 6.8 | 9.8 | 7.8 | 5.3 |
| ‘The experience with the stock market in the past few years:’ | (N=143) | (N=161) | (N=202) | (N=186) |
| ‘Much encouraged me to buy my house.’ | 13.9 | 15.5 | 14.3 | 9.1 |
| ‘Somewhat encouraged me to buy my house.’ | 11.1 | 16.7 | 13.8 | 13.9 |
| ‘Had no effect on my decision to buy my house.’ | 74.1 | 64.5 | 70.7 | 74.7 |
| ‘Somewhat discouraged me from buying my house.’ | 0.0 | 2.4 | 0.9 | 2.1 |
| ‘Much discouraged me from buying my house.’ | 0.6 | 0.6 | 0.0 | 0.0 |
The responses here present mixed evidence. In all four counties people believe that housing is indeed a better long-term investment than the stock market. However, the vast majority of people in all four counties said that the performance of the stock market ‘had no effect on my decision to buy my house’. Between a quarter and a third found the stock market's performance ‘encouraged’ them to buy a home while only a small proportion found it discouraging.
2.5 Rational expectations?
Table 9 gets to the meat of the issue of the role of price expectations in the decision to buy. Although virtually all Californians in 1988 knew that prices were going to rise in the next few years and were right, a mere 90 per cent thought so in 2002. The number who expected prices to rise jumped in Milwaukee to 95 per cent. After 21 years of steady increase, they are learning. While the number of respondents who thought prices were headed up in Boston dropped, it remains at 83 per cent.
| Question | Orange County | San Francisco | Boston | Milwaukee | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1988 | 2002 | 1988 | 2002 | 1988 | 2002 | 1988 | 2002 | ||||
| ‘Do you think that housing prices in the ________ area will increase or decrease over the next several years?’ |
(N=240) | (N=145) | (N=199) | (N=158) | (N=194) | (N=201) | (N=233) | (N=187) | |||
| ‘Increase’ | 98.3 | 89.7 | 99.0 | 90.5 | 90.2 | 83.1 | 87.1 | 95.2 | |||
| ‘Decrease’ | 1.7 | 10.3 | 1.0 | 9.5 | 9.8 | 16.9 | 12.9 | 4.8 | |||
| ‘How much of a change do you expect there to be in the value of your home over the next 12 months?’ |
(N=217) | (N=139) | (N=185) | (N=147) | (N=176) | (N=179) | (N=217) | (N=160) | |||
| Mean (Standard error) |
15.3 (0.8) |
10.5 (6.1) |
13.5 (0.6) |
5.8 (7.6) |
7.4 (0.6) |
7.2 (5.8) |
6.1 (0.5) |
8.9 (12.2) |
|||
| ‘On average over the next 10 years, how much do you expect the value of your property to change each year?’ |
(N=208) | (N=137) | (N=181) | (N=152) | (N=177) | (N=186) | (N=211) | (N=169) | |||
| Mean (Standard error) |
14.3 (1.2) |
13.1 (14.3) |
14.8 (1.4) |
15.7 (22.0) |
8.7 (0.6) |
14.6 (25.0) |
7.3 (0.5) |
11.7 (17.1) |
|||
| ‘Which of the following best describes the trend in home prices in the ____ area since January 1988?’ | (N=239) | (N=143) | (N=196) | (N=161) | (N=198) | (N=199) | (N=230) | (N=185) | |||
| ‘Rising rapidly’ | 90.8 | 76.2 | 83.7 | 28.6 | 3.0 | 29.6 | 8.7 | 33.0 | |||
| ‘Rising slowly’ | 8.8 | 22.4 | 12.8 | 51.0 | 34.3 | 49.2 | 53.0 | 57.3 | |||
| ‘Not changing’ | 0.4 | 1.4 | 3.1 | 14.3 | 37.4 | 12.6 | 23.9 | 8.6 | |||
| ‘Falling slowly’ | 0.0 | 0.0 | 0.5 | 6.2 | 22.2 | 8.5 | 11.7 | 1.1 | |||
| ‘Falling rapidly’ | 0.0 | 0.0 | 0.0 | 0.0 | 3.0 | 0.0 | 2.6 | 0.0 | |||
| ‘It's a good time to buy because housing prices are likely to rise in the future?’ | (N=206) | (N=126) | (N=180) | (N=145) | (N=171) | (N=174) | (N=210) | (N=161) | |||
| ‘Agree’ | 93.2 | 77.0 | 95.0 | 82.1 | 77.8 | 66.1 | 84.8 | 87.0 | |||
| ‘Disagree’ | 6.8 | 23.0 | 5.0 | 17.9 | 22.2 | 33.9 | 15.2 | 13.0 | |||
| ‘Housing prices are booming. Unless I buy now, I won't be able to afford a home later.’ | (N=200) | (N=124) | (N=167) | (N=134) | (N=169) | (N=175) | (N=194) | (N=154) | |||
| ‘Agree’ | 79.5 | 48.8 | 68.9 | 59.7 | 40.8 | 37.1 | 27.8 | 36.4 | |||
| ‘Disagree’ | 20.5 | 51.2 | 31.1 | 40.3 | 59.2 | 62.9 | 72.2 | 63.6 | |||
| ‘There has been a good deal of excitement surrounding recent housing price changes. I sometimes think that I may have been influenced by it.’ |
(N=230) | (N=141) | (N=191) | (N=156) | (N=181) | (N=199) | (N=233) | (N=184) | |||
| ‘Yes’ | 54.3 | 46.1 | 56.5 | 38.5 | 45.3 | 29.6 | 21.5 | 34.8 | |||
| ‘No’ | 45.7 | 53.9 | 43.5 | 61.5 | 54.7 | 70.4 | 78.5 | 65.2 | |||
| ‘In conversations with friends and associates over the last few months, conditions in the housing market were discussed.’ |
(N=238) | (N=143) | (N=195) | (N=163) | (N=198) | (N=203) | (N=235) | (N=185) | |||
| ‘Frequently’ | 52.9 | 32.9 | 49.7 | 37.4 | 30.3 | 31.0 | 20.0 | 27.6 | |||
| ‘Sometimes’ | 38.2 | 50.3 | 39.0 | 43.6 | 55.1 | 53.7 | 50.2 | 40.5 | |||
| ‘Seldom’ | 8.0 | 14.7 | 9.7 | 17.2 | 12.1 | 14.3 | 25.1 | 28.1 | |||
| ‘Never’ | 0.8 | 2.1 | 1.5 | 1.8 | 2.5 | 1.0 | 4.7 | 3.8 | |||
Home-buyers are very optimistic about the future of home prices. In fact, when asked about the average rate of increase per year over the next 10 years, in Orange County they replied 13.1 per cent (14.3 per cent in 1988); in San Francisco they were even more optimistic at 15.7 per cent (14.8 per cent in 1988); in Boston the answer was 14.6 per cent (8.7 per cent in 1988); and in Milwaukee it was 11.7 per cent (7.3 per cent in 1988). It is important to note, however, that the standard errors were much larger in 2002. In all four cities, expectations about house prices are not quite as optimistic about the next year as they are about the next 10 years. Nonetheless, buyers expect healthy increases also at this shorter horizon.
As in 1988, home-buyers' expectations about the future are backward-looking. The degree of their short-term optimism depends on their perceptions of what is happening now. Very few outside of Boston and Milwaukee in 1988 believed prices were falling at the time they bought. The pattern of belief about the present is consistent with their expectations for the next year, but their longer-run expectations were not.
While fewer respondents in 2002 say that it is a good time to buy a house because prices may be rising in the future, at least two-thirds of respondents agree with the statement in all four cities. In addition, the number who admit to being influenced by ‘excitement’ is down on the coasts but up to more than a third in Milwaukee. Finally, housing prices remain a frequent topic of conversation for many, the vast majority report at least sometimes discussing them.
2.6 Theories about recent events
Table 10 and an open-ended question were designed to probe people's interpretations of price movements and possible triggers that changed their opinions. It is critical to distinguish between mob psychology, excessive optimism and a situation in which a solid reason to expect price increases exists. Since most have expressed a strong investment motive, one would assume significant knowledge of underlying market fundamentals. The efficient market hypothesis assumes that asset buyers make rational decisions based on all available information and based on a consistent model of underlying market forces.
| Question | Orange County | San Francisco | Boston | Milwaukee | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1988 | 2002 | 1988 | 2002 | 1988 | 2002 | 1988 | 2002 | ||||
| ‘Housing prices have boomed in ____ because lots of people want to live here.’ |
(N=210) | (N=128) | (N=178) | (N=147) | (N=181) | (N=176) | (N=193) | (N=148) | |||
| ‘Agree’ | 98.6 | 93.8 | 93.3 | 89.1 | 69.6 | 77.8 | 16.1 | 23.0 | |||
| ‘Disagree’ | 1.4 | 6.2 | 6.7 | 10.9 | 30.4 | 22.2 | 83.9 | 77.0 | |||
| ‘The real problem in _____ is that there is just not enough land available.’ |
(N=197) | (N=121) | (N=174) | (N=141) | (N=168) | (N=177) | (N=192) | (N=158) | |||
| ‘Agree’ | 52.8 | 60.3 | 83.9 | 59.6 | 54.2 | 72.9 | 17.2 | 35.4 | |||
| ‘Disagree’ | 47.2 | 39.7 | 16.1 | 40.4 | 45.8 | 27.1 | 82.8 | 64.6 | |||
| ‘When there is simply not enough housing available, price becomes unimportant.’ |
(N=197) | (N=116) | (N=165) | (N=141) | (N=171) | (N=172) | (N=193) | (N=151) | |||
| ‘Agree’ | 34.0 | 31.9 | 40.6 | 32.6 | 26.9 | 32.0 | 20.7 | 25.2 | |||
| ‘Disagree’ | 66.0 | 68.1 | 59.4 | 67.4 | 73.1 | 68.0 | 79.3 | 74.8 | |||
| ‘Which of the following better describes your theory about recent trends in home prices in ____?’ |
(N=226) | (N=130) | (N=180) | (N=153) | (N=188) | (N=195) | (N=215) | (N=168) | |||
| ‘It is a theory about the psychology of home buyers and sellers.’ | 11.9 | 10.8 | 16.7 | 15.0 | 21.3 | 11.8 | 10.7 | 13.7 | |||
| ‘It is a theory about economic or demographic conditions such as population changes, changes in interest rates or employment.’ |
88.1 | 89.2 | 83.3 | 85.0 | 78.7 | 88.2 | 89.3 | 86.3 | |||
| ‘In a hot real estate market, sellers often get more than one offer on the day they list the property. Some are even over the asking price. There are also stories about people waiting in line to make offers. Which is the best explanation?’ | (N=210) | (N=135) | (N=177) | (N=153) | (N=176) | (N=197) | (N=211) | (N=173) | |||
| ‘There is panic buying, and price becomes irrelevant.’ | 73.3 | 63.7 | 71.2 | 73.9 | 61.4 | 73.1 | 34.6 | 46.8 | |||
| ‘Asking prices have adjusted slowly or sluggishly to increasing demand.’ | 26.7 | 36.3 | 28.8 | 26.1 | 38.6 | 39.9 | 65.4 | 53.2 | |||
There is mixed evidence in the results. First of all, Californians correctly think that a lot of people want to live there. Demand pressure is a factor in California. In Boston, the demographics are simply poor, yet 77.8 per cent of buyers in 2002 point to the idea that people want to live there. Both Boston and California residents point to a shortage of available land, and zoning has indeed been a big issue on the coasts. Demographics and a shortage of land have never been problems in Milwaukee, and buyers correctly perceive this.
At the time of the first survey, interest rates were flat to up, but they were having little effect on the market. Nonetheless, respondents to the open-ended question mentioned interest rates more than any other factor in explaining home prices. In 2002, interest rates were again mentioned most frequently in all four counties, but this time interest rates really were having an effect. Interest rates fell sharply in the months leading up to our survey, and they had a dramatic effect on affordability.
In 2002 over 85 per cent of respondents in each county say they have a theory of recent trends based on fundamentals, and fewer than 15 per cent point to the psychology of home-buyers. Only in Boston in 1988 did more than 20 per cent directly point to psychology. Having said that, a significant majority point to panic buying everywhere except in Milwaukee. These results are consistent with evidence in Pound and Shiller (1987) about institutional investors in corporate stocks, most of whom thought stock prices were driven by fundamentals even when particular stocks boomed and had very high PE ratios.
While it seems that home-buyers are reasonably well informed and perhaps better informed in 2002 than they were in 1988, one gets the impression from the responses that backward-looking price extrapolation is playing a major role in driving buyers' expectations of future price increases.
2.7 Excess demand and upward rigidity in asking prices
In boom cities, newspaper articles feature stories of homes that sold well above asking price. It was the article in the Wall Street Journal that referred to ‘frenzy in California's big single family home market’ that inspired our original survey. In fact, this seems to be a fairly common occurrence in boom cities. An amazing 45 per cent of respondents report selling at above asking prices in San Francisco in 2002 (Table 11), well after the sharp decline in employment following the NASDAQ collapse which began in 2000. Sellers report that about 20 per cent of properties sell for more than the asking price in Orange County and this figure was only slightly smaller in Milwaukee, which had no boom.
| Question | Orange County | San Francisco | Boston | Milwaukee | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1988 | 2002 | 1988 | 2002 | 1988 | 2002 | 1988 | 2002 | ||||
| ‘Did you finally settle on the price that was:’ |
(N=237) | (N=141) | (N=194) | (N=153) | (N=200) | (N=203) | (N=242) | (N=183) | |||
| ‘Above the asking price’ | 6.3 | 19.9 | 9.8 | 45.8 | 0.5 | 21.3 | 3.3 | 17.5 | |||
| ‘Equal to the asking price’ | 38.0 | 50.4 | 26.8 | 27.5 | 23.5 | 59.1 | 22.7 | 52.4 | |||
| ‘Below the asking price’ | 55.7 | 29.7 | 63.4 | 26.7 | 76.0 | 28.6 | 74.0 | 31.1 | |||
| ‘If you had asked 5 to 10 per cent more for your property, what would the likely outcome have been?’ |
(N=89) | (N=68) | (N=64) | (N=59) | (N=61) | (N=83) | (N=43) | (N=46) | |||
| ‘It wouldn't have been sold.’ | 21.3 | 23.5 | 23.4 | 27.1 | 31.1 | 27.7 | 32.5 | 26.1 | |||
| ‘It would have sold but it would have taken much more time.’ | 44.9 | 47.1 | 46.9 | 40.7 | 54.1 | 38.6 | 37.2 | 39.3 | |||
| ‘If buyers had to pay that much they might not be able to obtain financing (a buyer cannot obtain financing unless an appraiser confirms the worth of the property).’ | 7.9 | 4.1 | 9.4 | 6.8 | 0.0 | 4.8 | 9.3 | 8.7 | |||
| ‘It probably would have sold almost as quickly.’ | 24.7 | 23.5 | 17.2 | 20.3 | 11.5 | 26.5 | 16.3 | 21.7 | |||
| ‘Other’ | 1.1 | 1.5 | 3.1 | 5.1 | 3.3 | 2.4 | 4.7 | 4.4 | |||
| ‘If you answered that it would have sold almost as quickly, which of the following (you can check more than one) explains why you didn't set the price higher?’ | (N=37) | (N=31) | (N=22) | (N=26) | (N=26) | (N=37) | (N=16) | (N=15) | |||
| ‘The property simply wasn't worth that much.’ | 32.4 | 25.8 | 27.3 | 23.1 | 38.5 | 13.5 | 25.0 | 13.3 | |||
| ‘It wouldn't have been fair to set it that high; given what I paid for it. I was already getting enough for it.’ | 16.2 | 25.8 | 22.7 | 61.5 | 15.4 | 54.1 | 31.3 | 46.7 | |||
| ‘I simply made a mistake or got bad advice; I should have asked for more.’ | 21.6 | 19.4 | 18.2 | 7.7 | 19.2 | 8.1 | 25.0 | 13.3 | |||
| ‘Other’ | 29.7 | 29.0 | 31.8 | 7.7 | 26.9 | 24.3 | 18.8 | 26.7 | |||
| ‘In the six months prior to the time you first listed the property, did you receive any unsolicited calls from a real estate agent or any one else about the possibility of selling your house?’ | (N=89) | (N=68) | (N=61) | (N=63) | (N=62) | (N=83) | (N=48) | (N=44) | |||
| ‘Yes’ | 71.9 | 69.1 | 59.0 | 55.6 | 38.7 | 53.0 | 43.2 | ||||
| ‘No’ | 28.1 | 30.9 | 41.0 | 44.4 | 61.3 | 46.0 | 56.8 | ||||
| Approximate number of calls | |||||||||||
| Mean (Standard error) |
8.7 (1.2) |
5.0 (0.3) |
3.9 (0.4) |
2.7 (0.2) |
|||||||
Many of those who sold felt that they could have gotten more also thought that if they had charged 5 or 10 per cent more, the property would have sold just as quickly. This was the sense of over 20 per cent of sellers in all markets, up substantially in 2002 except in Orange County where it stayed the same.
An amazing number of respondents, in fact a majority in San Francisco and Boston in 2002, a near majority in Milwaukee and 26 per cent in Orange County thought that charging more would be unfair. However, the number who reported that their house was not intrinsically worth more than they were asking dropped in the latest survey compared to 1988.
2.8 Downward rigidity and excess supply
An important question on which the survey sheds some light is what happens in a bust? How do sellers respond to rising inventories and increasing time on the market? It is first important to point out that the housing market is not a traditionally-defined auction market. Prices do not fall to clear the market quickly as one observes in most asset markets. Selling a home requires agreement between buyers and sellers. It is a stylised fact about the housing market that ‘bid-ask’ spreads widen when demand drops, and the number of transactions falls sharply. This must mean that sellers resist cutting prices.
The survey does indeed support the fact that buyers lower their asking prices only as a last resort. A majority in all counties and in both years of the survey argued that the best strategy in a slow market is to ‘hold up until you get what you want’ (Table 12). In fact, only a small minority of respondents reported that they would have ‘lowered the price till I found a buyer’. In addition, from 78.8 per cent in San Francisco in 1988 to 93 per cent in post-boom Boston reported having reservation prices.
| Question | Orange County | San Francisco | Boston | Milwaukee | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1988 | 2002 | 1988 | 2002 | 1988 | 2002 | 1988 | 2002 | ||||
| ‘Since housing prices are unlikely to drop very much, the best strategy in a slow market is to hold up until you get what you want for a property.’ |
(N=174) | (N=111) | (N=148) | (N=129) | (N=160) | (N=166) | (N=180) | (N=147) | |||
| ‘Agree’ | 69.0 | 64.0 | 69.6 | 69.0 | 57.5 | 51.2 | 50.6 | 61.9 | |||
| ‘Disagree’ | 31.0 | 36.0 | 30.4 | 31.0 | 42.5 | 48.8 | 49.4 | 38.1 | |||
| ‘If you had not been able to sell your property for the price that you received, what would you have done?’ |
(N=88) | (N=65) | (N=62) | (N=61) | (N=61) | (N=83) | (N=43) | (N=43) | |||
| ‘Left the price the same and waited for a buyer, knowing full well that it might have taken a long time.’ |
42.0 | 32.3 | 38.7 | 29.5 | 32.8 | 21.7 | 32.6 | 39.5 | |||
| ‘Lowered the price step by step hoping to find a buyer’ |
20.5 | 32.3 | 38.7 | 26.2 | 42.6 | 47.0 | 20.9 | 30.2 | |||
| ‘Lowered the price till I found a buyer.’ |
4.5 | 7.7 | 3.2 | 11.5 | 4.9 | 12.0 | 7.0 | 9.3 | |||
| ‘Taken the house off the market.’ |
18.2 | 21.5 | 17.7 | 27.9 | 11.5 | 15.7 | 27.9 | 16.3 | |||
| ‘Other’ | 14.8 | 6.2 | 1.6 | 4.9 | 8.2 | 3.6 | 11.6 | 4.6 | |||
| ‘If you answered that you would have lowered your price, is there a limit to how far you would have gone if the property still hadn't sold?’ |
(N=33) | (N=35) | (N=38) | (N=32) | (N=29) | (N=57) | (N=16) | (N=32) | |||
| ‘Yes’ | 81.8 | 85.7 | 78.9 | 81.3 | 93.1 | 87.7 | 87.5 | 90.3 | |||
There is clear evidence that such resistance prevents house prices from falling at the onset of a down period and that if the underlying fundamentals come back quickly enough, it can prevent a bubble from ‘bursting’. Instead, the danger when demand drops in housing markets is that the volume of sales may drop precipitously. The fallout would include: lower consumption from a reduction in the equity withdrawal that frequently accompanies housing changes; a reduction in the consumer expenditures that are associated with changing housing; reduced fee income to financial institutions; and a reduction in the flexibility of the labour market. These and other related effects could do more damage to the US economy today than a modest decline in prices.
3. Differential Wealth Effects from Housing and Equities: Theories and Evidence
The results of the sample survey discussed above suggest that households may be subject to various behavioural biases (e.g., irrational expectations about future price growth that are excessively affected by recent trends) that may contribute to the large swings in house prices that are apparent in the data. The question then arises as to whether these swings in house prices also have significant effects on aggregate activity via their impacts on household wealth. Ultimately, however, this is an empirical question. Accordingly, the remainder of the paper assesses the extent to which movements in house prices have wealth effects on consumption, and whether these wealth effects are quantitatively different to effects arising from swings in equity prices.
A simple formulation of the life cycle savings hypothesis suggests that consumers will distribute increases in anticipated wealth over time and that the marginal propensity to consume out of all wealth, whether from stocks, real estate, or any other source, should be the same small number, something just over the real interest rate. Clearly, such a proportionate effect must exist in the long run. However, there are a number of concerns about the identification of the short-run effects of changes in wealth on household spending.
There are, in fact, many reasons why consumption may be differently affected by the form in which wealth is held. First, increases in measured wealth of different kinds may be viewed by households as temporary or uncertain. Second, households may have a bequest motive which is strengthened by tax laws that favour holding appreciated assets until death. Third, households may view the accumulation of some kinds of wealth as an end in and of itself. Fourth, households may not find it easy to measure their wealth, and may not even know what it is from time to time. The unrealised capital gains held by households in asset markets may be transitory, but they can be measured with far more precision in thick markets with many active traders. Fifth, people may segregate different kinds of wealth into separate ‘mental accounts’, which are then framed quite differently. The psychology of framing may dictate that certain assets are more appropriate to use for current expenditures while others are earmarked for long-term savings (Shefrin and Thaler 1988).
Each of these concerns suggests a distinction between the impact of housing wealth and stock market wealth on consumption. The extent to which people view their currently-measured wealth as temporary or uncertain may differ between the two forms of wealth. People may have quite different motives about bequeathing their stock portfolios and bequeathing their homesteads to heirs. The emotional impact of accumulating stock market wealth may be quite different from that of real estate wealth, particularly owner-occupied housing. People are, perhaps, less aware of the short-run changes in real estate wealth since they do not receive regular updates on its value. Stock market wealth can be tracked daily in the newspaper.
Differential impacts of various forms of wealth on consumption have already been demonstrated in a quasi-experimental setting. For example, increases in unexpected wealth in the form of lottery winnings lead to large effects on short-run consumption. Responses to surveys about the uses put to different forms of wealth imply strikingly different ‘wealth effects’. By analogy, it is entirely reasonable to expect that there should be a different impact of real estate and housing wealth, as compared with stock market wealth, on consumption.
Exogenous changes in housing wealth could also have an impact different from lottery winnings or stock market windfalls by affecting the consumption behaviour of renters or younger cohorts of consumers. An exogenous increase in house values and housing wealth means that these latter groups of households must save more today to become home-owners tomorrow. In principle, some or all of the increased consumption made by current owners could be offset by increased savings of renters who aspire to become home-owners (see Sheiner (1995)).
The empirical importance of housing wealth for consumption has not been widely explored. An early study by Elliott (1980) relied upon aggregate data on consumer spending, financial wealth, and non-financial wealth, finding that variations in the latter had no effect upon consumption. Elliott's analysis suggested that ‘houses, automobiles, furniture, and appliances may be treated more as part of the environment by households than as a part of realisable purchasing power’ (p 528). These results were challenged by Peek (1983) and by Bhatia (1987) who questioned the methods used to estimate real non-financial wealth. More recently, Case (1992) reported evidence of a substantial consumption effect during the real estate price boom in the late 1980s using aggregate data for New England.
Using data on individual households from the Panel Study of Income Dynamics (PSID), Skinner (1989) found a small but significant effect of housing wealth upon consumption. Sheiner (1995) explored the possibility noted above that home price increases may actually increase the savings of renters who then face higher downpayment requirements to purchase houses. Her statistical results, however, were quite inconclusive.
A more suggestive relationship was reported by Yoshikawa and Ohtake (1989) who found that savings rates for Japanese renter households planning to purchase homes was higher with higher land prices, but that the incidence of household plans to purchase housing was sufficiently lower with higher land prices, so that the net effect of higher prices was to increase consumption by renters as well as owners.
Analogous results were found for renters in Canada by Engelhardt (1994); higher housing prices substantially reduced the probability that renter households saved for a downpayment. A C$4,000 increase in house prices decreased the probability of saving by 1 percentage point, and led to a reduction in accumulated assets of C$1,200.
From surveys of US home-buyers assembled by a major title and trust company, it was estimated that transfers from family members provided downpayment assistance for 20 per cent of first-time home-buyers, accounting, on average for half of the first payment (Engelhardt and Mayer 1998). Transfers from others reduced household savings by 30–40 cents per US dollar (see also Engelhardt and Mayer (1994)).
Thus it appears that higher housing prices reduce, rather than increase, the savings of renters. Moreover, to the extent that higher housing prices increase the resources (leveraged at almost four to one) available for intra-familial transfers, this further reduces the savings of those renters who expect to become home-owners.
Engelhardt (1996) also provided a direct test of the link between house price appreciation and the consumption of current home-owners, also using the PSID. He estimated that the marginal propensity to consume out of real capital gains in owner-occupied housing is about 0.03, but this arose from an asymmetry in behavioural response. Households experiencing real gains did not change their savings and consumption behaviour appreciably, while those experiencing capital losses did reduce their consumption behaviour.
Much of the limited evidence on the behavioural response to changes in housing wealth has arisen from consideration of the ‘savings puzzle’. During the late 1990s, personal savings as measured in the National Income and Product Accounts fell sharply, to about zero in 2000. But it was shown that if unrealised capital gains in housing were included in both the income and savings of the household sector (as suggested by the original Haig-Simons criteria), then the aggregate personal savings rates computed were much higher (Gale and Sabelhaus 1999).
Similarly, Hoynes and McFadden (1997) used micro (PSID) data to investigate the correlation between individual savings rates and rates of capital gains in housing. Consistent with the perspective of Thaler (1990), the authors found little evidence that households were changing their savings in non-housing assets in response to expectations about capital gains in owner-occupied housing.
The only other study of the ‘wealth effect’ which has disaggregated housing and stock market components of wealth is an analysis of the Retirement History Survey by Levin (1998). Levin found essentially no effect of housing wealth on consumption.
All of these micro studies of consumer behaviour rely upon owners' estimates of housing values. Evidence does suggest that the bias in owners' estimates is small (see below), but these estimates typically have high sampling variances (Kain and Quigley 1972; Goodman and Ittner 1992). This leaves much ambiguity in the interpretation of statistical results.
4. Data for Wealth and Consumption
We address the linkage between stock market wealth, housing wealth, and household consumption using two distinct bodies of panel data that have been assembled in parallel for this purpose. The datasets have different strengths and weaknesses, which generally complement each other for the study of these relationships.
The first dataset consists of a panel of quarterly data constructed for US states from 1982 through 1999. This panel exploits the fact that the distribution of increases in housing values has been anything but uniform across regions in the US, and the increases in stock market wealth have been quite unequally distributed across households geographically. This panel offers the advantage that data definitions and institutions are uniform across geographical units. In addition, the sample size is large. One disadvantage of this dataset arises because one key variable must be imputed to the various states on the basis of other data measured at the state level. Another disadvantage of these data is that the US stock market has trended upwards during the entire sample period, and the period may have been unusual (Shiller 2000).
The second body of data consists of a panel of annual observations on 14 developed countries for various years during the period of 1975–1999. This dataset relies upon consumption measures derived from national income accounts, not our imputations, but we suspect that housing prices and housing wealth in this panel are measured less accurately. In addition, the sample of countries with consistent data is small. Finally, there are substantial institutional differences among countries, for example, variations in the taxation of wealth and capital gains and in institutional constraints affecting borrowing and saving.
Both datasets contain substantial time series and cross-sectional variation in cyclical activity and exhibit substantial variation in consumption and wealth accumulation.
4.1 US state data
We estimate stock market wealth, housing market wealth and consumption for each US state, quarterly, for the period 1982–1999.
Estimates of aggregate financial wealth were obtained annually from the Federal Reserve Flow of Funds (FOF) accounts and compared to the aggregate capitalisation of the three major US stock markets. From the FOF accounts, we computed the sum of corporate equities held by the household sector, pension fund reserves, and mutual funds. The FOF series has risen in nominal terms from under US$2 trillion in 1982 to US$18 trillion in 1999. It is worth noting that more than half of the gross increase between 1982 and 1999 occurred during the 4 years between 1995 and 1999. The total nominal increase for the 13 years between 1982 and 1995 was US$7.5 trillion; the total nominal increase during the 4 years between 1995 and 1999 was an astonishing US$8.4 trillion. Nearly all variation in the FOF aggregate arises from variation in the capitalisation of the stock market. To distribute household financial assets geographically, we exploit the correlation between holdings of mutual funds and other financial assets. We obtained mutual fund holdings by state from the Investment Company Institute (ICI). The ICI data are available for the years 1986, 1987, 1989, 1991 and 1993. We assumed that for 1982:Q1 through 1986:Q4, the distribution was the same as it was in 1986; similarly we assumed that the 1993 distribution held for the period 1993–1999. We further assumed that direct household holdings of stocks and pension fund reserves were distributed in the same geographical pattern as mutual funds. These are clearly strong assumptions, but there are no alternative data.
Estimates of housing market wealth were constructed from repeat sales price indices similar to those described in Section 2, from Fiserv Case Shiller Weiss, Inc. where available, and otherwise from indices produced by Fannie Mae and Freddie Mac. One difference is that the data used here are based on the base values reported in the 1990 Census of Population and Housing by state.
Equation (2) indicates how the panel on aggregate housing wealth was constructed for each state

where
Vit = aggregate value of owner-occupied housing in state i in quarter t,
Rit = home-ownership rate in state i in quarter t,
Nit = number of households in state i in quarter t,
Iit = weighted repeat sales price index, Fiserv Case Shiller Weiss, Inc. or OFHEO, for state i in quarter t (Ii1 = 1, for 1990:Q1), and
Pio = mean home price for state i in the base year, 1990.
The total number of households N as well as the home-ownership rates R were obtained from the Current Population Survey conducted by the US Census Bureau annually and interpolated for quarterly intervals. Aggregate wealth varies as a result of price appreciation of the existing stock as well as additions to the number of owner-occupied dwellings.
As noted above, the baseline figures for state level mean home prices Pio are derived from estimates of house values reported in the 1990 Census. Several studies have attempted to measure the bias in owner estimates of house values. The estimates range from −2 per cent (Follain and Malpezzi 1981; Kain and Quigley 1972) to +6 per cent (Goodman and Ittner 1992). However, Goodman and Ittner point out that for many purposes, owners' estimates may indeed be the appropriate measures of housing wealth; household consumption and savings behaviour is likely to be based upon perceived home value.
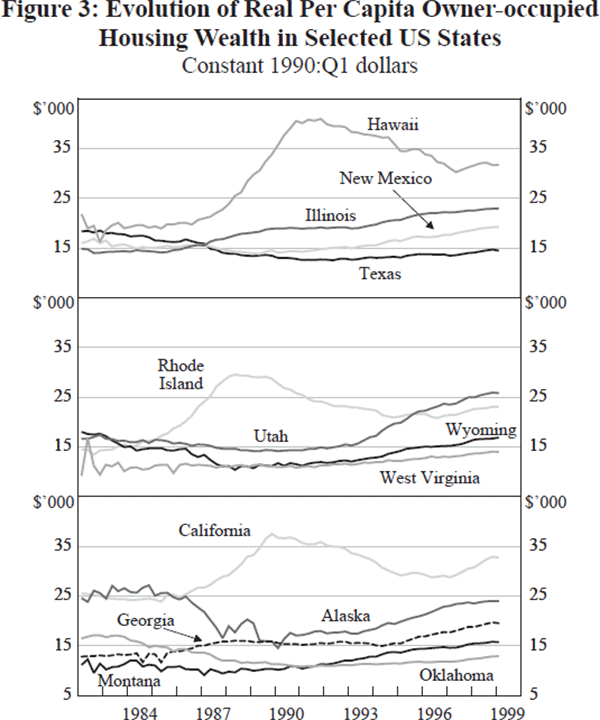
The aggregate nominal value of the owner-occupied stock in the US grew from US$2.8 trillion in 1982 to US$7.2 trillion in 1999. Figure 3 reports the evolution of real per capita owner-occupied housing wealth during the period 1982–1999. There is considerable variation in the course of housing wealth across states. For the states illustrated, the levels vary by 300 per cent, and the timing of changes varies substantially.
Unfortunately, there are no measures of consumption spending by households recorded at the state level. However a panel of retail sales has been constructed by Regional Financial Associates (RFA; now Economy.com). Retail sales account for roughly half of total consumer expenditures.[4] The RFA estimates were constructed from county level sales tax data, the Census of Retail Trade published by the US Census Bureau, and the Census Bureau's monthly national retail sales estimates. For states with no retail sales tax or where data were insufficient to support imputations, RFA based its estimates on the historical relationship between retail sales and retail employment. Data on retail employment by state are available from the Bureau of Labor Statistics. Regression estimates relating sales to employment were benchmarked to the Census of Retail Trade available at five-year intervals. Estimates for all states were within 5 per cent of the benchmarks.
Retail sales can be expected to differ systematically from consumption spending for several reasons. Clearly, in states with relatively large tourist industries, recorded retail sales per resident are high. Nevada, for example, with 26 per cent of its labour force employed in tourism, recorded per capita retail sales of US$3,022 in 1997:Q1, third-highest among the 50 states. In addition, states with low or no sales tax can be expected to have high retail sales per resident. For example, New Hampshire with no sales tax, recorded per capita retail sales of US$3,200 in 1997:Q1, highest among the 50 states. Most states, however, were more tightly clustered around the mean of US$2,385 in 1997:Q1.
While there are systematic differences between retail sales and consumption, to the extent that the differences are state-specific, this can be accounted for directly in multivariate statistical analysis. Data on retail sales, house values, and stock market valuation, by state and quarter, were expressed per capita in real terms using the Current Population Survey and the GDP deflator.
4.2 International data
It was possible to obtain roughly comparable data for a panel of 14 developed countries during the period 1975–1996.[5] In an analogous manner, we estimate stock market wealth, housing market wealth, and consumption for each country for each year.
Estimates of aggregate stock market wealth for each country were obtained from the Global Financial Database, which reports domestic stock market capitalisation annually for each country. To the extent that the fraction of the stock market wealth owned domestically varies among countries, this can be accounted for in the statistical analysis reported below by permitting fixed effects to vary across countries. We can introduce country-specific time trends to control for variations over time in home-country investment bias, by country.
Estimates of housing market wealth were constructed in a manner parallel to those used for the panel of US states which are summarised in Equation (2). Indices of annual housing prices Iit were obtained from the Bank of International Settlements (BIS), which consolidated housing prices reported for some 15 industrialised countries (see Kennedy and Andersen (1994) or Englund and Ionnides (1997)). The BIS series for the US was quite short, so the national OFHEO-Freddie Mac series described earlier is used for the US.
Consistent data on housing prices for a benchmark year, Pio, were not available for the panel of countries. This means that regression estimates without fixed effects for each country (which control for country-specific benchmarks) are meaningful only under very restrictive assumptions.
Data on the number of owner-occupied housing units were obtained from various issues of the Annual Bulletin of Housing and Building Statistics for Europe and North America published by the United Nations. The series describing the owner-occupied housing stock was not complete for some years in all the countries. More complete data existed for the total housing stock of each country. Where missing, the owner-occupied housing stock was estimated from the total housing stock reported for that year and the ratio of the owner-occupied housing stock to the total housing stock for an adjacent year. Missing data points were estimated by linear interpolation.[6]
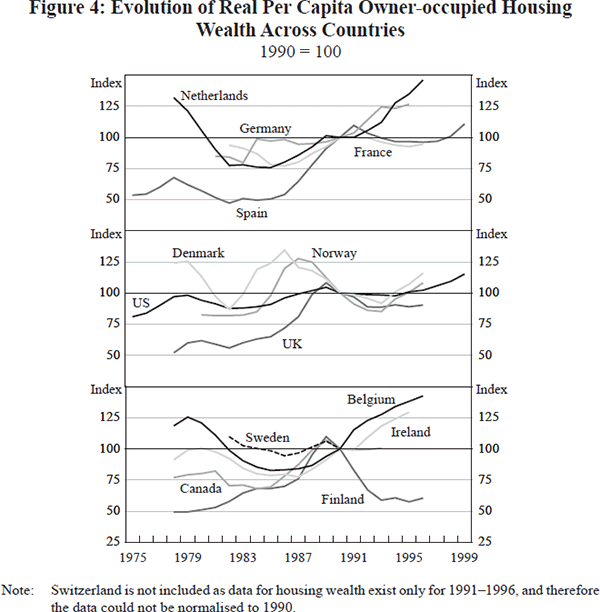
Figure 4 reports the evolution of housing market wealth in the 14 countries relative to its aggregate value in 1990. The variations over time in housing market wealth are striking.
Consumption data were collected from the International Financial Statistics database. ‘Household Consumption Expenditure including Nonprofit-Institution-Serving Households’ is used for the European Union countries that rely upon the European System of Accounts (ESA1995). ‘Private Consumption’ is used for other countries, according to the System of National Accounts (SNA93). Data on aggregate consumption, housing values and stock market valuations, by country and year, were expressed per capita in real terms using UN population data and the consumer price index.
5. Results from Estimating Wealth Effects on Consumption
Tables 13 through 16 report various econometric specifications of the relationship. All include fixed effects, i.e. a set of dummy variables for each country and state. Model II for each specification also includes state- and country-specific time trends. Model III includes year-specific fixed effects as well as fixed effects for countries and states. For the panel of states, Model III also includes seasonal fixed effects, i.e., one for each quarter. In each of the four tables, the first three columns present regression results for the panel of countries (228 observations on 14 countries), while the next three columns report the results for the panel of states (3498 observations on 50 states and the District of Columbia).[7] Table 13 presents basic ordinary least squares relationships between per capita consumption, income, and the two measures of wealth. As the table indicates, in the simplest formulation, the estimated effect of housing market wealth on consumption is significant and large. In the international comparison, the elasticity ranges from 0.11 to 0.17. In the cross-state comparison, the estimated elasticity is between 0.05 and 0.09. In contrast, the estimated effects of financial wealth upon consumption are smaller. In the simplest model, the estimate from the country panel is 0.02. In the other two regressions, the estimated coefficient is insignificantly different from zero, perhaps reflecting the more restricted ownership of non-financial wealth in Western European countries. In the cross-state comparisons, the estimated effect of financial wealth is highly significant, but its magnitude is about 60 per cent as large as the estimated effect of housing wealth.
| Country data | State data | ||||||
|---|---|---|---|---|---|---|---|
| I | II | III | I | II | III | ||
| Income | 0.660 (9.69) |
0.349 (5.63) |
0.287 (3.27) |
0.567 (31.95) |
0.705 (28.56) |
0.559 (22.84) |
|
| Stock market wealth | 0.019 (2.05) |
0.002 (0.25) |
−0.010 (−0.87) |
0.056 (14.19) |
0.028 (5.86) |
0.063 (10.53) |
|
| Housing market wealth | 0.131 (5.33) |
0.110 (7.35) |
0.166 (6.90) |
0.084 (11.56) |
0.047 (6.97) |
0.086 (11.57) |
|
| Country/state-specific time trends | No | Yes | No | No | Yes | No | |
| Year/quarter fixed effects | No | No | Yes | No | No | Yes | |
| R2 | 0.9991 | 0.9998 | 0.9993 | 0.9241 | 0.9587 | 0.9305 | |
| t-ratio | 4.664 | 7.090 | 6.987 | 3.919 | 2.408 | 2.541 | |
| p-value for H0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.016 | 0.011 | |
| p-value for H1 | 1.000 | 1.000 | 1.000 | 1.000 | 0.992 | 0.994 | |
| Notes: The equations all contain country/state fixed effects. All variables are in real per capita terms (deflated by GDP deflator) and measured in logarithms; t-ratios are shown in parentheses. The country data are annual observations for 1975–1999. The state data are quarterly observations for 1982–1999. H0 is a test of the hypothesis that the coefficient on housing market wealth is equal to that of stock market wealth. H1 is a test of the hypothesis that the coefficient on housing market wealth exceeds that of stock market wealth. |
|||||||
The table also reports the t-ratio for the hypothesis that the difference between the coefficient estimates measuring housing and financial market effects is zero. A formal test of the hypothesis that the coefficient on housing market wealth is equal to that of stock market wealth (against the alternative hypothesis that the two coefficients differ) is presented, as well as a test of the hypothesis that the coefficient on housing market wealth exceeds the coefficient on financial wealth. The evidence suggests that housing market wealth has a more important effect on consumption than does financial wealth.
Table 14 reports the results when the effects of first order serial correlation are also estimated.[8] The estimated serial correlation coefficient is highly significant and large in magnitude. The coefficients of housing market wealth change only a little. For the panel of countries, the estimated elasticity ranges from 0.11 to 0.14; for the panel of states, the estimate ranges from 0.04 to 0.06. In five of the six regressions reported, the hypothesis that the effects of housing market wealth are larger than those of financial wealth is accepted by a wide margin.
| Country data | State data | ||||||
|---|---|---|---|---|---|---|---|
| I | II | III | I | II | III | ||
| Income | 0.679 (12.30) |
0.309 (4.84) |
0.388 (5.07) |
0.647 (40.20) |
0.432 (18.16) |
0.336 (13.94) |
|
| Stock market wealth | 0.007 (1.16) |
−0.004 (−0.69) |
−0.003 (−0.33) |
0.042 (11.87) |
0.007 (1.53) |
0.026 (4.87) |
|
| Housing market wealth | 0.108 (4.62) |
0.115 (6.52) |
0.136 (5.92) |
0.039 (4.14) |
0.054 (6.25) |
0.062 (6.96) |
|
| Serial correlation coefficient | 0.854 (23.77) |
0.564 (9.57) |
0.817 (19.49) |
0.878 107.43) |
0.784 (73.55) |
0.866 (101.44) |
|
| Country/state-specific time trends | No | Yes | No | No | Yes | No | |
| Year/quarter fixed effects | No | No | Yes | No | No | Yes | |
| R2 | 0.9998 | 0.9999 | 0.9998 | 0.9839 | 0.9855 | 0.9863 | |
| t-ratio | 4.282 | 6.525 | 5.987 | −0.311 | 4.543 | 3.425 | |
| p-value for H0 | 0.000 | 0.000 | 0.000 | 0.756 | 0.000 | 0.001 | |
| p-value for H1 | 1.000 | 1.000 | 1.000 | 0.378 | 1.000 | 1.000 | |
| Notes: See Table 13. | |||||||
Table 15 presents results with all variables expressed as first differences. In this formulation, the coefficient on housing market wealth is significant in all specifications, while the coefficient of financial wealth is essentially zero. Consumption changes are highly dependent on changes in income and housing wealth, but not stock market wealth.
| Country data | State data | ||||||
|---|---|---|---|---|---|---|---|
| I | II | III | I | II | III | ||
| Income | 0.266 (4.06) |
0.239 (3.49) |
0.254 (3.34) |
0.332 (14.12) |
0.325 (13.73) |
0.274 (11.15) |
|
| Stock market wealth | −0.008 (−1.37) |
−0.010 (−1.67) |
−0.007 (−0.97) |
0.001 (0.23) |
0.002 (0.36) |
0.003 (0.50) |
|
| Housing market wealth | 0.128 (6.21) |
0.147 (6.56) |
0.141 (6.37) |
0.034 (3.58) |
0.030 (3.11) |
0.038 (3.94) |
|
| Country/state-specific time trends | No | Yes | No | No | Yes | No | |
| Year/quarter fixed effects | No | No | Yes | No | No | Yes | |
| Regression R2 | 0.3943 | 0.4346 | 0.4807 | 0.0729 | 0.0813 | 0.1458 | |
| Durbin-Watson | 1.718 | 1.847 | 1.705 | 2.424 | 2.445 | 2.484 | |
| t-ratio | 6.341 | 6.725 | 6.518 | 2.876 | 2.437 | 3.097 | |
| p-value for H0 | 0.000 | 0.000 | 0.000 | 0.004 | 0.015 | 0.002 | |
| p-value for H1 | 1.000 | 1.000 | 1.000 | 0.998 | 0.993 | 0.999 | |
| Notes: See Table 13. | |||||||
Unit root tests suggest that, although we can accept stationarity for most of the series, non-stationarity may be a problem for some series.[9] Therefore, Table 16 presents the model in first differences including the lagged (log) ratio of consumption to income. This is the error-correction model (ECM) often employed in the presence of unit roots. The model represents a co-integrated relation between consumption and income, where income includes income from the stock market and housing. Note that the lagged ratio of consumption to income has a coefficient that is negative and significant in all regressions for both panels. Thus, transitory shocks, arising from changes in other variables in the model or the error term in the regression, will have an immediate effect on consumption but will eventually be offset unless the shocks are ultimately confirmed by income changes. Again, the results support the highly significant immediate effect of housing market wealth upon consumption; the effect is especially large relative to that of financial wealth.[10]
| Country data | State data | |||||||
|---|---|---|---|---|---|---|---|---|
| I | II | III | I | II | III | |||
| Change in income | 0.283 (4.33) |
0.297 (4.77) |
0.274 (3.64) |
0.350 (14.92) |
0.388 (16.61) |
0.304 (12.57) |
||
| Change in stock market wealth | −0.003 (−0.59) |
0.001 (0.26) |
−0.004 (−0.58) |
−0.009 (−2.02) |
−0.009 (−2.06) |
−0.003 (−0.51) |
||
| Change in housing market wealth | 0.097 (4.25) |
0.100 (4.36) |
0.107 (4.35) |
0.044 (4.33) |
0.047 (4.60) |
0.054 (5.23) |
||
| Lagged change in consumption | 0.131 (2.17) |
0.117 (2.01) |
0.150 (2.32) |
−0.182 (−10.75) |
−0.149 (−8.75) |
−0.227 (−13.44) |
||
| Lagged ratio of consumption to income |
−0.077 (−2.65) |
−0.333 (−7.04) |
−0.071 (−2.45) |
−0.049 (−6.87) |
−0.151 (−14.00) |
−0.051 (−6.77) |
||
| Country/state-specific time trends | No | Yes | No | No | Yes | No | ||
| Year/quarter fixed effects | No | No | Yes | No | No | Yes | ||
| R2 | 0.4248 | 0.5634 | 0.5044 | 0.1301 | 0.1787 | 0.2169 | ||
| Durbin-Watson | 1.858 | 1.897 | 1.898 | 2.028 | 2.009 | 2.055 | ||
| t-ratio | 4.176 | 4.044 | 4.369 | 4.305 | 4.539 | 4.727 | ||
| p-value for H0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| p-value for H1 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | ||
| Notes: This table shows estimates of the following
equation: ΔCt = αΔCt−1 + β1ΔInct + β2ΔStockt + β3ΔHouset + γ [Ct−1 – Inct−1] + FixedEffects + εt. See notes to Table 13. |
||||||||
6. Conclusion
In previous work we have highlighted the role of the expectations and attitudes of households in determining outcomes in the housing market. This paper has provided additional new evidence on the importance of such factors. The most important result from our survey of home-buyers in four US cities in 2002 is that it suggests that home-buyers' expectations are substantially affected by recent experience. Even after a long boom, home-buyers typically have expectations that prices over the next 10 years will show double-digit annual price growth, apparently only with a modest level of risk. It seems reasonable to conjecture that an expectations formation process such as this could well be a major contributor to the substantial swings seen in housing prices in some US regions.
Given the importance of housing in household wealth, it also seems reasonable to conjecture that the observed swings in housing prices could have substantial macroeconomic impacts. We have examined the wealth effects from both housing and equities with two panels of cross-sectional time-series data that enable more comprehensive tests than in any earlier work. The numerical results vary somewhat with different econometric specifications, and so any quantitative conclusion must be tentative. Nevertheless, the evidence of a stock market wealth effect is weak; the common presumption that there is strong evidence for this form of a wealth effect is not supported in our results. However, we do find strong evidence that variations in housing market wealth have important effects upon consumption. This evidence arises consistently using panels of US states and industrial countries and is robust to differences in model specification. Interestingly, our modeling approach of using a panel of states has recently been applied to Australia by Dvornak and Kohler (2003), who also find a significant effect of housing on consumption.
Looking ahead, the two main findings of this paper suggest that any weakness in the US housing market would have an important impact on the macroeconomy. Our survey (and other evidence) point to some factors that might mitigate these effects. In particular, the reluctance of sellers to lower their asking prices may limit the magnitude of any fall in prices, and if the underlying fundamentals came back quickly enough, it might prevent a bubble from ‘bursting’. On the other hand, there is the danger that when demand drops in housing markets, the volume of sales may drop precipitously, which could do more damage to the US economy today than a modest decline in prices.
Footnotes
Prepared for the Reserve Bank of Australia conference on Asset Prices and Monetary Policy, Sydney, 18–19 August 2003. Karl E Case is the Katherine Coman and A Barton Hepburn Professor of Economics at Wellesley college. John M Quigley is the I Donald Terner Distinguished Professor, and Professor of Economics, at the University of California, Berkeley. Robert J Shiller is the Stanley B Resor Professor of Economics at Yale University and Researcher, NBER. This paper has benefited from the assistance of Victoria Borrego, Tanguy Brachet, George Korniotis, Sonya Lai, Maryna Marynchenko and Semida Munteanu. [1]
Indeed, in a speech to the Mortgage Bankers Association, Federal Reserve Chairman Alan Greenspan has ruminated: ‘One might expect that a significant portion of the unencumbered cash received by [house] sellers and refinancers was used to purchase goods and services … However, in models of consumer spending, we have not been able to find much incremental explanatory power of such extraction. Perhaps this is because sellers’ extraction [of home equity] is sufficiently correlated with other variables in the model, such as stock-market wealth, that the model has difficulty disentangling these influences' (Greenspan 1999). [2]
While the Office of Federal Housing Enterprise Oversight (OFHEO) uses a similar index construction methodology (the weighted repeat sales measure of Case and Shiller (1987), their indices are in part based on appraisals rather than exclusively on arms-length transactions. Case-Shiller indices use controls, to the extent possible, for changes in property characteristics, and it can be shown that they pick up turns in price direction earlier and more accurately than do the OFHEO indices. [3]
In 1997, for example, gross domestic product was US$8.08 trillion, household consumption spending was US$5.49 trillion, and retail sales amounted to US$2.63 trillion. [4]
The countries include: Belgium (1978–1996), Canada (1978–1993), Denmark (1978–1996), Finland (1978–1996), France (1982–1996), Germany (1991–1995), Ireland (1982–1987, 1994–1995), Netherlands (1978–1996), Norway (1980–1996), Spain (1975–1996), Sweden (1975–1996), Switzerland (1991–1996), the UK (1978–1996), and the US (1975–1997). [5]
In addition, we are grateful for unpublished estimates of the stock of owner-occupied housing supplied by Taltavull de La Paz (2001) for Spain and the value of owner-occupied housing by Barot and Yang (2002) for Sweden. [6]
The state panel is not quite balanced. The series includes quarterly observations from 1982:Q1 through 1999:Q4 for all states but Arizona. The time series for Arizona begins in 1987:Q1. [7]
These models rely on sequential estimation using the Prais-Winsten estimator. [8]
Augmented Dickey-Fuller tests, both with and without an intercept and a trend, can reject a unit root for most of the series, but not all. This finding is consistent with tests for a common unit root (Maddala and Wu 1999) which can reject the presence of a common unit root for all four variables (and both datasets), suggesting that at least one of the series is stationary. [9]
Our data measure financial and housing values at the end of each period, rather than their averages throughout each period. Therefore, we estimated each of the 24 regressions reported in Tables 13 through 16 using one- and two-period leads and lags in the measures of housing and financial assets. The character of these results is consistent with those reported in the text: measures of housing wealth were significant; measures of financial wealth were sometimes insignificant; and the magnitude of the coefficient on housing wealth exceeded that of financial wealth. These results are robust. [10]
References
Barot B and Z Yang (2002), ‘House prices and housing investment in Sweden and the United Kingdom: econometric analysis for the period 1970–1998’, National Institute of Economic Research Working Paper No 80.
Bhatia K (1987), ‘Real estate assets and consumer spending’, Quarterly Journal of Economics, 102(2), pp 437–444.
Case KE (1983), ‘The market for single-family homes in the Boston area’, New England Economic Review, May/June, pp 38–48.
Case KE (1992), ‘The real estate cycle and the economy: consequences of the Massachusetts boom of 1984–87’, Urban Studies, 29(2), pp 171–183.
Case KE and RJ Shiller (1987), ‘Prices of single-family homes since 1970: new indexes for four cities’, New England Economic Review, Sept/Oct, pp 45–56.
Case KE and RJ Shiller (1988), ‘The behavior of home buyers in boom and post-boom markets’, New England Economic Review, Nov/Dec, pp 29–46.
Case KE and RJ Shiller (1989), ‘The efficiency of the market for single-family homes’, American Economic Review, 79(1), pp 125–137.
Case KE and RJ Shiller (1990),‘Forecasting prices and excess returns in the housing market’, American Real Estate and Urban Economics Association Journal, 18(3), pp 253–273.
Dvornak N and M Kohler (2003), ‘Housing wealth, stock market wealth and consumption: a panel analysis for Australia’, Reserve Bank of Australia Research Discussion Paper No 2003-07.
Elliott JW (1980), ‘Wealth and wealth proxies in a permanent income model’, Quarterly Journal of Economics, 95(3), pp 509–535.
Engelhardt GV (1994), ‘House prices and the decision to save for down payments’, Journal of Urban Economics, 36(2), pp 209–237.
Engelhardt GV (1996), ‘House prices and home owner saving behaviour’, Regional Science and Urban Economics, 26(3–4), pp 313–336.
Engelhardt GV and CJ Mayer (1994), ‘Gifts for home purchase and housing market behaviour’, New England Economic Review, May/June, pp 47–58.
Engelhardt GV and CJ Mayer (1998), ‘Intergenerational transfers, borrowing constraints, and savings behaviour: evidence from the housing market’, Journal of Urban Economics, 44(1), pp 135–157.
Englund P and YM Ioannides (1997), ‘House price dynamics: an international empirical perspective’, Journal of Housing Economics, 6(2), pp 119–136.
Follain JR and S Malpezzi (1981), ‘Are occupants accurate appraisers?’, Review of Public Data Use, 9(1), pp 47–55.
Gale WG and J Sabelhaus (1999), ‘Perspectives on the household saving rate’, Brookings Papers on Economic Activity, 1, pp 181–214.
Goodman JL and JB Ittner (1992), ‘The accuracy of home owners' estimates of house value’, Journal of Housing Economics, 2(4), pp 339–357.
Greenspan A (1999), ‘Mortgage finance’, remarks delivered to Mortgage Bankers' Association, Washington DC, 8 March.
Hoynes HW and DL McFadden (1997), ‘The impact of demographics on housing and nonhousing wealth in the United States’, in MD Hurd and Y Naohiro (eds), The economic effects of aging in the United States and Japan, NBER Conference Report Series, University of Chicago Press, Chicago, pp 153–194.
Kain JF and JM Quigley (1972), ‘Note on owners' estimates of housing values’, Journal of American Statistical Association, 67(340), pp 803–806.
Kennedy N and P Andersen (1994), ‘Household saving and real housing prices: an international perspective’, BIS Working Paper No 20.
Levin L (1998), ‘Are assets fungible? Testing the behavioral theory of life-cycle savings’, Journal of Economic Behavior and Organization, 36(1), pp 59–83.
Maddala GS and S Wu (1999), ‘A comparative study of unit root tests with panel data and a new simple test’, Oxford Bulletin of Economics and Statistics, 61, Special Issue, pp 631–652.
Peek J (1983), ‘Capital gains and personal saving behavior’, Journal of Money, Credit, and Banking, 15(1), pp 1–23.
Pound J and RJ Shiller (1987), ‘Are institutional investors speculators?’, Journal of Portfolio Management, 13(3), pp 46–52.
Shefrin HM and RH Thaler (1988), ‘The behavioral life-cycle hypothesis’, Economic Inquiry, 26(4), pp 609–643.
Sheiner L (1995), ‘Housing prices and the savings of renters’, Journal of Urban Economics, 38(1), pp 94–125.
Shiller RJ (2000), Irrational exuberance, Princeton University Press, Princeton.
Skinner J (1989), ‘Housing wealth and aggregate saving’, Regional Science and Urban Economics, 19(2), pp 305–324.
Taltavull de La Paz P (2001), ‘Housing and consumption in Spain’, paper presented at the 8th Annual ERES Conference, Alicante, 26–29 June.
Thaler RH (1990), ‘Anomalies: saving, fungibility and mental accounts’, Journal of Economic Perspectives, 4(1), pp 193–205.
Yoshikawa H and F Ohtake (1989), ‘An analysis of female labor supply, housing demand, and the saving rate in Japan’, European Economic Review, 33(5), pp 997–1023.