RBA Annual Conference – 2003 Asset Prices, Financial Imbalances and Monetary Policy: Are Inflation Targets Enough? Charles Bean[1]
Abstract
Some commentators have argued that an exclusive focus of monetary policy on achieving price stability is inappropriate in a world where asset-price misalignments and financial imbalances are increasingly prevalent. This paper reviews the argument that monetary policy should react to asset-price movements and/or financial imbalances over and above their impact on the inflation outlook. I conclude that, while monetary policy-makers should take note of such developments, the macroeconomic implications can be adequately embraced within an appropriately flexible and forward-looking concept of inflation targets. In a simple New Keynesian model, modified to allow for capital and debt accumulation, I then show that the possibility of credit crunches may affect the design of the optimal policy in subtle and unexpected ways. I also consider a variety of other ways that incipient financial imbalances could impinge on the conduct of an optimal monetary policy. Finally I discuss recent developments in the UK household sector as a practical example of the problem of assessing whether an asset price is misaligned and whether balance sheet developments pose a threat to the outlook.
1. Introduction
On the face of it, the last decade and a half has been a successful period for most developed-country central banks. Compared to the previous 15 years, inflation has been low and relatively stable. Moreover, price stability has not been achieved at the expense of the real economy, as growth has also been relatively stable and unemployment has been falling in a number of countries.
Notwithstanding the good macroeconomic out-turns there has, however, been a growing concern that the achievement of price stability may be associated with heightened risks of financial instability, particularly so in the aftermath of the collapse of the dot com bubble and the more recent wider correction to share values. Appreciating asset values and debt accumulation have, in some countries, led to stretched household and corporate balance sheets that are vulnerable to the sort of equity-price corrections witnessed recently. That has led some commentators to question the quasi-consensus that monetary policy should be directed exclusively at maintaining price stability and its role in combating financial instability should be restricted to minimising any adverse consequences when over-valuations are corrected or as financial imbalances unwind.
The heterodox view is neatly summarised by Crockett (2003; italics in original):
(I)n a monetary regime in which the central bank's operational objective is expressed exclusively in terms of short-term inflation, there may be insufficient protection against the build up of financial imbalances that lies at the root of much of the financial instability we observe. This could be so if the focus on short-term inflation control meant that the authorities did not tighten monetary policy sufficiently pre-emptively to lean against excessive credit expansion and asset price increases. In jargon, if the monetary policy reaction function does not incorporate financial imbalances, the monetary anchor may fail to deliver financial stability.
In this paper I examine the view that inflation targeting alone, whether explicit or implicit, is not enough and that there is a case for an additional monetary response to asset-price movements and/or developing financial imbalances in order to reduce the risks of future financial instability. My view, in a nutshell, is that (flexible) inflation targeting is best thought of as a description of the objective function of the policy-maker rather than entailing an explicit monetary policy reaction function. The abrupt unwinding of asset-price misalignments and/or financial imbalances that may lead to financial instability will also invariably be associated with significant macroeconomic instability. A forward-looking flexible inflation-targeting central bank should bear in mind those longer-run consequences of asset-price bubbles and financial imbalances in the setting of current interest rates. Consequently there is no need to require an additional response of monetary policy, though inflation-targeting central banks may need to look out further into the future than is customary in order to take on board these concerns.
The remainder of the paper is organised as follows. In the next section, I review some of the recent literature on the extent to which monetary policy should respond to asset prices, and in particular to asset-price bubbles. While it may well be appropriate for interest rates to respond to asset prices, among many other economic indicators, I conclude that such a response is consistent with inflation targeting. In the subsequent section I characterise the optimal monetary policy in a simple New Keynesian macroeconomic model in which financial imbalances play a role and where their subsequent unwinding may lead to a credit crunch or similar financial distress. The possibility of credit crunches turns out to affect the design of the optimal policy in a subtle, and perhaps surprising, way. I also consider a variety of other ways that incipient financial imbalances could impinge on the conduct of an optimal monetary policy. Finally I illustrate some of the difficulties in deciding whether an asset price is misaligned, or an imbalance poses a potential threat to macroeconomic stability, by considering the recent evolution of house prices and consumer debt in the United Kingdom.
2. Asset Prices and Monetary Policy: Some Recent Views
The conventional view that monetary policy can do little more than deal with the fall-out from the unwinding of asset-price bubbles has been clearly enunciated by Chairman Greenspan (2002):
Such data suggest that nothing short of a sharp increase in short-term rates that engenders a significant economic retrenchment is sufficient to check a nascent bubble. The notion that a well-timed incremental tightening could have been calibrated to prevent the late 1990s bubble is almost surely an illusion. Instead, we … need to focus on policies to mitigate the fallout when it occurs and, hopefully, ease the transition to the next expansion.
But not everyone subscribes to this view, and there has recently been a lively literature debating the extent to which monetary policy should respond to asset-price movements (see e.g. Batini and Nelson (2000); Bernanke and Gertler (2000, 2001); Cecchetti et al (2000); Cecchetti, Genberg and Wadhwani (2003); Taylor (2001)). Thus on the one hand Bernanke and Gertler (2000) conclude that:
The inflation targeting approach dictates that central banks should adjust monetary policy actively and pre-emptively to offset incipient inflationary and deflationary pressures. Importantly for present purposes, it also implies that policy should not respond to changes in asset prices, except insofar as they signal changes in expected inflation.
Against this, Cecchetti et al (2000) argue:
A central bank concerned with both hitting an inflation target at a given time horizon, and achieving as smooth a path as possible for inflation, is likely to achieve superior performance by adjusting its policy instruments not only to inflation (or its inflation forecast) and the output gap, but to asset prices as well. Typically modifying the policy framework in this way could also reduce output volatility. We emphasise that this conclusion is based on our view that reacting to asset prices in the normal course of policymaking will reduce the likelihood of asset price bubbles forming, thus reducing the risk of boom-bust investment cycles.
Each of these contributions evaluate the appropriateness of a policy response to asset prices by exploring the efficacy of a variety of interest rate reaction functions in simple calibrated stochastic model economies in which asset prices play some explicit role. Thus both Bernanke and Gertler (2000, 2001) and Cecchetti et al (2000) employ a dynamic New Keynesian model, modified to allow for credit market frictions and exogenous asset-price bubbles. The credit market frictions arise from agency problems in the credit market, so that internal finance is cheaper than external finance and the external finance premium depends on the firm's financial position. In particular a rise in the firm's share price increases the available collateral and leads to a reduction in the marginal cost of external funds, and a consequent increase in borrowing and investment. Furthermore, the equity price may differ from fundamentals by an exogenous and stochastic bubble component, which grows exponentially but may collapse. During the build-up of such a bubble the external finance premium falls, and investment, aggregate demand and future potential output rise, whereas when the bubble collapses the processes reverses.
But despite the apparent similarity of the models employed, the two sets of authors come to strikingly different conclusions about whether it is wise for the monetary authorities to condition their short-term interest rate on the equity price. Cecchetti et al (2000) argue that a key difference lies in different assumptions about what shocks are present and exactly what the monetary authorities are allowed to observe.
Similarly, Batini and Nelson explore whether a response to the exchange rate (which may or may not contain a bubble) is advisable in an open-economy setting in which the real exchange rate influences both demand and supply and the exchange rate is determined via uncovered interest parity. For an optimised rule they find no gain in reacting to exchange rate movements. Yet Cecchetti et al (2000), using essentially the same model, find that under some circumstances responding to the exchange rate does lead to higher welfare. Again the key difference appears to lie in the assumptions about what shocks are present and exactly what the monetary authorities know.
Now at one level it is not surprising that different assumptions about the stochastic structure of the economy and what the authorities can observe/infer may lead to different conclusions about the advisability of linking interest rates to asset-price movements. And few people would disagree that the authorities should take account of asset-price movements insofar as they affect the outlook for output and inflation. But the question is whether some additional response is called for, as the above quotes should make clear. In addressing this issue, it is helpful to look first at the analytical framework these authors employ.
Essentially all these contributions evaluate whether the addition of asset prices – or an estimate of the bubble component therein – to a simple feedback rule for the policy rate instrument leads to a lower value of a suitable loss function. Two general classes of simple rules are employed. Either an augmented Taylor rule:

where it is the nominal interest rate, i*t is the ‘natural’ level of the nominal interest rate, Πt is inflation (strictly, the deviation from target), xt is the deviation of output from its flexible-price level, i.e. the output gap, and qt is an asset price (relative to some suitably defined normal or equilibrium value). Or else an augmented inflation-forecast-targeting rule:

where Et denotes the mathematical expectation conditional on information available to the policy-maker at time t and k is some suitably chosen time horizon.
The authorities are assumed to have an objective function that is quadratic in the deviation of inflation from target and in the output gap:
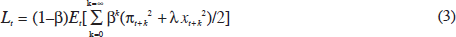
where β is a discount factor. As β tends to unity, so this loss function tends to a simple weighted average of the conditional variances of inflation about the target and of the output gap. The authors then, in essence, search over the parameters in the Taylor-type rule (1) and/or the inflation-forecast-targeting rule (2) to find the values of the feedback coefficients that minimise the loss function (3).
However, it is worth recalling that, despite their appeal, Taylor-type rules imply feedback from a relatively restricted state vector and the optimal feedback rule can only be written as a Taylor rule in very simple settings. The same is true of inflation-forecast-targeting rules, which furthermore are dynamically inconsistent (see Svensson (2001)). A relevant question is why we should be interested in whether an asset price, or indeed any other variable for that matter, appears in some ad hoc class of feedback rule, even though the coefficients of that rule may have been optimised? It seems more instructive to ask first what an optimal rule looks like, and then consider how asset prices ought to figure in it. One might then go on to consider whether particular simple rules represent sufficiently close approximations to the optimal rule to be useful guideposts for policy.
In order to say more we need to assume something about the structure of the economy. Suppose, for illustrative purposes, the demand side is given by a New Keynesian IS schedule, including the asset price:
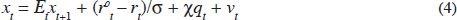
where rt (≡ it – EtΠt+1) is the real interest rate, rot is the flexible-price, or natural, real interest rate and vt is an aggregate demand shock. The IS schedule is augmented by a suitable intertemporal arbitrage condition determining the asset price (including, perhaps, a bubble component or a stochastic risk premium). And the supply side is given by a New Keynesian Phillips curve:

where ut is a supply (cost) shock. Both shocks are observed by the monetary authorities and for simplicity are assumed to be serially uncorrelated.
Then, as shown by Svensson and Woodford (2003), Svensson (2002), Giannoni and Woodford (2002) and others, the optimal policy under discretion satisfies the first-order condition:

This dictates that policy should ‘lean against the wind’ in the event of supply shocks, but that demand shocks are neutralised. However, in optimising over the choice of coefficients in the simple rule (1)/(2), the existing literature implicitly assumes that the central bank has access to a suitable commitment technology. In that case, the appropriate comparison should be against the optimal policy under commitment (from the ‘timeless perspective’), which satisfies the set of first-order conditions, for all k ≥ 0:
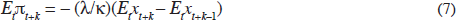
The optimal plan thus equates the marginal rate of transformation between output and inflation that is embodied in the supply schedule with the marginal rate of substitution that is embodied in the loss function. It ensures that inflation will be brought back to target, but at a rate that recognises the consequences for activity. Svensson has characterised an optimality condition of this type as describing ‘flexible inflation-forecast targeting’. Note that even though there are no lagged endogenous variables in the model, the optimal policy is nevertheless history-dependent.[2] This property plays an important role in Section 3 below.
A key feature of these optimality conditions is that they contain neither the policy instrument[3], nor indeed anything to do with the structure of the demand side of the economy. In particular there is no role for asset prices. This observation would hold true for more general specifications of the economy, provided that the asset price affects neither the marginal rate of transformation nor the marginal rate of substitution.[4] So in that sense the analysis supports the conventional wisdom as summarised in the quote above from Bernanke and Gertler – with the modification that policy responds to changes in asset prices only insofar as they signal changes in expected inflation or activity.
Is this a reasonable interpretation of what inflation-targeting central banks are about, as opposed to an inflation-forecast-targeting rule like (2)? Take for instance the statutory objective of the Bank of England since it was given operational independence in 1997. The Bank of England Act (1998) charges the Bank ‘to maintain price stability, and subject to that to support the economic policy of (the) government, including the objectives for growth and employment’. An annual ‘Remit’ from the Chancellor of the Exchequer then defines price stability – currently as an annual rate of inflation of 2.5 per cent for RPIX at all times[5] – and also fleshes out the ‘economic policy of the government’, namely the maintenance of a high and stable rate of growth. This can be thought of as defining the bliss point for inflation, but instructing the Monetary Policy Committee to seek to achieve it in a way that avoids undue volatility in economic activity. However, the remit is non-specific about the relative weight that we should put on deviations of output from potential and deviations of inflation from target. Both King (1997) and Bean (1998) discuss the UK inflation-targeting regime in these terms; the latter also explores the consequences of the incompleteness of the remit.
Similarly the objectives of the Reserve Bank of Australia (RBA) as laid out in the Reserve Bank Act (1959) are ‘to ensure that … monetary and banking policy … is directed … [so as to] contribute to: … the stability of the currency … the maintenance of full employment … and … the economic prosperity and welfare of the people …’. The counterpart of the UK Remit from the Chancellor in Australia is the joint Second Statement on the Conduct of Monetary Policy between the Governor and the Treasurer. The target is for an inflation rate for the underlying CPI of 2–3 per cent ‘over the cycle’. Again the ‘first-level’ target for inflation is specified explicitly, together with a general injunction that the central bank should care about the level of activity. I think this view of what monetary policy-makers are seeking to achieve is also a fair description of central banks like the Federal Reserve or the European Central Bank that do not describe themselves explicitly as inflation targeters.
But that does leave open the extent to which asset prices should affect the setting of the instrument, because they will affect the outlook for growth and inflation. Given the relevant optimality condition, the IS schedule (Equation (4)) can be used to back out the associated value of the instrument, it. Clearly this reaction function in general will contain the asset price, qt. That is consistent with the views of Cecchetti et al (2000), though the finding that the inclusion of asset prices in an augmented Taylor or inflation-forecast-targeting rule reduces the expected loss does not imply an independent role for asset prices beyond their impact on the outlook for inflation and activity. And, in fairness to Cecchetti et al, they never really claim it does.
The substantive issue that divides those who advocate a more activist response to asset prices from those who do not, is really the extent to which asset-price movements are informative about the prospects for inflation and growth, and whether pre-emptive action against a bubble is either possible or effective. Here it is worth recalling the difficulty of establishing significant and stable econometric relationships between asset prices and subsequent movements in output or inflation; see e.g. Stock and Watson (2001) for a recent survey. But there are good reasons why such links should be unstable as asset prices can move for a variety of reasons, each of which may have different implications for growth and inflation.
For instance, even if valued according to their fundamentals, equity prices could fall because of a reduction in expected future earnings, an increase in the expected risk-free discount rate, or a change in the equity risk premium. And that reduction in earnings might come about because of, for example, a fall in the expected rate of growth of productivity, an increase in corporate taxes, or an increase in product market competition. And finally equity prices may include a non-fundamental or bubble component. But these various shocks all have rather different implications for growth and inflation, either qualitatively or quantitatively.
That suggests that an automatic response to any single asset price is likely to be in general inappropriate, as stressed by Goodfriend (2003). As an aside we might note that this applies not only to equity prices, but also to exchange rates. Monetary Conditions Indices (MCIs) that weight together nominal interest rates and the exchange rate are often used to indicate whether monetary conditions have changed, on the argument that a fall in the exchange rate – seen as a monetary variable – boosts demand in the same way as does a reduction in nominal interest rates. But this ignores the fact that the exchange rate can change for a variety of reasons, including shifts in preferences or productive potential at home or abroad, changes in current or expected interest rates, changes in portfolio preferences and risk premia, and bubbles and fads. The nature of the shock, as well as the initial degree of over- or under-valuation of the exchange rate, will affect the pass-through into activity and inflation and consequently the appropriate monetary response.
The danger in following an MCI too closely in setting policy is well illustrated by the experience of New Zealand during the Asia crisis. At that time the Reserve Bank of New Zealand (RBNZ) employed an MCI as an operating target for the implementation of monetary policy. As a consequence the depreciation of the New Zealand dollar during 1997–98 led more or less automatically to an increase in domestic interest rates. But the depreciation of the Kiwi dollar was part of a more general depreciation of currencies in the region, and was associated with a contraction in the markets for New Zealand exports. A more appropriate monetary response would have been to reduce interest rates – as the RBA did – rather than to raise them. Australia's subsequent economic performance was noticeably superior to that of New Zealand, and the RBNZ abandoned an MCI as an operating target the following year.
But the fact that asset prices may move for a variety of reasons is not a justification for ignoring them completely. Rather, as stressed by Cecchetti et al (2000), it is an argument for using the full array of asset prices and other information in order to try to extract an estimate of the underlying shocks driving them. Policy-makers are already used to trying to draw such inferences from the co-movements of a set of variables, and even an imperfect estimate of the underlying shocks is better than ignoring the information altogether. The case for exploiting the information contained in asset prices thus seems irrefutable in principle, though the difficulties involved in doing so are considerable and due recognition needs to be paid to the imprecision of the resulting estimates.
As to the possibility of preventing asset-price bubbles and misalignments through pre-emptive action, I am rather more sceptical. As with the more general problem of imbalances discussed below, early diagnosis of such problems is fraught with difficulties. Once one can be fairly confident that a bubble has emerged, it is probably too late to take significant action against it without causing just the disruption to the real economy that one wants to avoid. If one is confident that an asset-price bubble will continue, then one might want to raise interest rates in order to try to moderate it. But the presence of lags between an interest rate change and its effect on the real economy means that if one expects the bubble to burst imminently, then policy relaxation is appropriate now in order to prepare for the fallout. Tightening policy to deal with an asset-price bubble may thus end up being counterproductive if the bubble then bursts, so that the economy is subject to the twin deflationary impulses of an asset-price collapse and the lagged policy tightening. Gruen, Plumb and Stone (this volume) explore this issue and show that the informational requirements necessary to make such activist policy effective are extreme. At best there seems likely to be only a very narrow window of opportunity during which action is likely to be effective.
3. Financial Imbalances and Monetary Policy
Borio and Lowe (2002) argue persuasively that the issue is not really whether monetary policy should respond to asset-price bubbles per se. Rather booms and busts in asset prices – which may reflect the presence of bubbles, but may also reflect shifts in assessments of the underlying fundamentals – should be seen as part of a broader set of symptoms that typically also include a build-up of debt and frequently a high rate of capital accumulation. Thus during a period of exuberance – irrational or otherwise – optimism about future returns drives up asset values, prompting private agents to borrow in order to finance capital accumulation. Moreover, appreciating asset values raise the value of collateral, hence facilitating the accumulation of debt. During the upswing, balance sheets may look healthy as the appreciation in asset values offsets the build-up of debt. But if that optimism turns to pessimism, leading to a correction in asset valuations and a sharp deterioration in net worth, then financial distress may be the result as the financial imbalances are exposed. That is particularly likely if financial intermediaries respond to the deterioration in their own, and their creditors', balance sheets by tightening credit conditions. This process may apply to the corporate sector and productive capital, but may equally well apply to the household sector and housing capital.
Borio and Lowe also argue that while low and stable inflation may promote financial stability overall, such financial imbalances can nevertheless build up in a low-inflation environment. Indeed beneficial supply shocks – resulting either from faster productivity growth or from structural or institutional reform – are likely both to lower inflationary pressure and to foster the build-up of such imbalances. And that may be aggravated when monetary policy has a high degree of counter-inflationary credibility as excessive expansion in aggregate demand beyond the natural rate of output may have only limited impact on inflationary pressures.
In order to explore some of the implications of debt-financed asset accumulation for the conduct of monetary policy, I shall employ a simple New Keynesian macroeconomic model of the sort considered above, modified to allow for debt-financed capital accumulation and the possibility of credit crunches.
There are two types of agents in the economy: households and firms. Households supply labour and save a constant fraction of their income. They also own a non-tradable diversified portfolio of shares in firms, so that all profits are returned to households in lump-sum form. Firms are monopolistic competitors, and nominal prices are fixed with a fraction of prices being reset each period as in the standard New Keynesian Phillips curve. Capital lasts a single period, is installed a period in advance, and is financed entirely by borrowing from households. Debt lasts a single period and is denominated in real terms.
Credit crunches occur with a fixed probability, ρ. When they do occur their effect is to lower the level of supply in the economy. One rationalisation for this assumption could be that a credit crunch leads to bankruptcies and the necessary administration or reorganisation of the firm's assets absorbs resources. Another could be that firms need access to working capital within the period in order to pay their workers, buy inputs, etc. If firms cannot get access to the required working capital then their supply will necessarily be curtailed. In effect a credit crunch is thus treated as a negative shock to total factor productivity, though it reflects events in financial markets rather than a change in the technical capabilities of the economy.
Moreover, if a credit crunch does occur, it is assumed to be more severe the higher is the overall debt outstanding. It is this feature that provides the incentive for the central bank to moderate a current debt-financed investment boom. Since an individual firm's borrowing decision has negligible impact on overall debt, firms ignore the impact of their borrowing on the severity of any future credit crunch, i.e. there is a negative externality present. Of course, in that case the first-best policy would be to invoke other policies that tackle the market failures more directly, such as prudential capital requirements, etc. Nevertheless, it seems fruitful for central bankers to ask how monetary policy should be conducted in a second-best world where those market failures remain.
The equations of the model are developed in the Appendix, but can be reduced to a conventional New Keynesian Phillips curve, as in Equation (5), and a forward-looking IS schedule:

This is similar to the standard New Keynesian IS schedule, though its interpretation is somewhat different. In particular the terms on the right-hand side reflect the determinants of investment, rather than consumption as in the standard approach. A high level of expected future output increases the marginal product of capital, thus encouraging investment, while it is discouraged by a high cost of capital. Likewise the shock, vt, can be thought of as reflecting the ‘animal spirits’ of entrepreneurs.
Now consider the central bank's control problem. Crucially we assume the objective is to stabilise output around its technically feasible level, i.e. the natural rate of output that would obtain in the absence of a credit crunch. In the Appendix it is shown that the output gap relative to the natural rate that would apply in the absence of a credit crunch, x*t, can be expressed as:
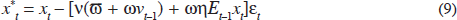
where εt is an indicator variable that takes the value unity (zero) if a credit crunch occurs (does not occur) and the other Greek symbols are parameters (ϖ and ω parameterise the cost of a credit crunch, and η and ν are functions of tastes and technology). The quantity in square brackets represents the output cost of a credit crunch, with terms reflecting the fact that debt carried into the period will be high if ‘animal spirits’ had been buoyant in the preceding period or if output had been expected to be high.
It is noteworthy that the impact of the credit crunch is not affected directly by the rate of interest in the preceding period. A higher rate of interest reduces capital formation and debt accumulation during period t–1, but that is exactly nullified by the higher interest payments on the debt. Consequently the total amount that has to be repaid is left unchanged. In general whether an increase in the rate of interest in period t–1 raises or lowers the debt stock in period t depends on the semi-elasticity of borrowing with respect to the interest rate. In the present example the assumption of a Cobb-Douglas technology ensures that this is unity, so that the two effects exactly offset. This means that the effect of monetary policy today on the severity of any future credit crunch must operate entirely through its impact on the expected future level of activity.
First consider the case when the central bank is unable to commit. In the Appendix it is shown that the optimal monetary policy can be characterised by the optimality condition:

This is analogous to Equation (6), except that it is written in terms of the output gap measured relative to the level of potential output that would obtain in the absence of a credit crunch. Thus in the absence of a credit crunch (i.e., x*t = xt), policy is unaffected by the possibility of credit crunches in the future. If, on the other hand, there is a credit crunch in period t (i.e., x*t < xt), policy is set looser than it would otherwise be. So policy is in effect as espoused by Chairman Greenspan in the quotation at the start of Section 2 (though perhaps for a different reason): ignore the bubble in the upswing, but mitigate the fallout if and when it bursts. Furthermore the possibility of such a loose monetary policy in the face of a credit crunch tomorrow will raise expected inflation today. Consequently, even in the absence of a credit crunch there will be an upward bias to inflation today.
The reason that the possibility of future credit crunches does not affect policy in the upswing directly (there is an indirect effect via inflation expectations) is quite simple. Tightening policy today has no effect of the debt-income ratio that obtains tomorrow, because the reduction in investment and borrowing is exactly counterbalanced by the higher interest payments entailed. The only way the debt-income ratio can be affected is by lowering expectations of future activity, but this is impossible when the monetary authorities cannot precommit.
Now suppose the monetary authorities can precommit. In the Appendix it is shown that the ‘timelessly optimal’ plan under commitment satisfies the optimality conditions (for all t and for all k ≥ 0):
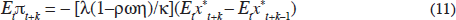
The structural similarity to the model of Section 2 – obtained by setting ρ to zero – makes it easy to see the impact of the possibility of a credit crunch on policy design. Assuming that ρωη < 1, introducing the possibility of a credit crunch is similar in effect to reducing the weight on output in the central bank's objective function (compare also with Equation (7)).
That there is apparently less incentive to stabilise current output when the economy is overheating and building up larger imbalances today[6] may appear counter-intuitive. However, recall that this model is forward-looking in nature. And, though an increase in interest rates today cannot affect the severity of a credit crunch tomorrow because the interest semi-elasticity of borrowing is unity, policy does affect debt levels through another channel, namely expectations of the future output gap. The expectation of a large positive output gap tomorrow thus boosts capital accumulation today, so raising the future debt stock and the costs associated with a credit crunch.
Now, as noted in Section 2, optimal policy in the standard New Keynesian model without credit crunches is history-dependent despite the absence of any backward-looking structural dynamics. That is because the optimal policy exploits the fact that a credible commitment to hold output above potential in the future raises inflation today via the expectations term in the Phillips curve. Thus, given the convexity of the loss function, the optimal response to a temporary supply disturbance involves a small, but persistent, output gap, rather than returning inflation straight away to target through a larger, but more short-lived, one. Demand shocks are contemporaneously and fully neutralised, of course.
When there is a possibility of a credit crunch, however, the gradualist response to, say, a beneficial supply shock generates additional expected future costs in the shape of a more severe credit crunch, should one occur. Consequently the optimal policy involves a less accommodative policy today, i.e. more variation in the current output gap, and less persistence than in the standard set-up. Moreover, the optimal policy under commitment involves a weaker monetary policy response to the occurrence of a credit crunch than is the case under discretion. That is because the central bank recognises that a policy of accommodating credit crunches through the loosening of monetary policy has adverse effects on inflation expectations. Consequently there is less monetary response to a credit crunch than under discretion, but average inflation is lower. There are echoes here of the supposed dangers of the ‘Greenspan put’ (see Miller, Weller and Zhang (2002)).
Of course this model is rather simple and omits some important channels whereby policy can influence the accumulation and unwinding of imbalances. Consequently the results may not be robust (though Groth (2003) develops a somewhat different model that shares some of the same characteristics). Nevertheless the analysis illustrates the fact that allowing for such phenomena in a forward-looking setting may affect the design of policy in subtle, as well as more obvious, ways.
One aspect that is missing from the analysis is an explicit role for asset prices. Falling asset prices reduce collateral and may induce a sharp change in the behaviour of potential borrowers as collateral constraints start to bind. That can act as an important amplification and propagation mechanism, as in the work of Kiyotaki and Moore (1997). Bordo and Jeanne (2002) construct a model in which firms can only borrow against collateral, and a credit crunch occurs if asset prices fall sufficiently. As in the model of this paper, the credit crunch then leads to a loss of output. But the resulting model is highly non-linear, and Bordo and Jeanne show that an appropriately forward-looking policy that responds to the initial asset-price inflation and build-up of debt by pre-emptively raising interest rates[7] dominates a purely reactive policy that responds to current inflation and activity.
Bordo and Jeanne go on to conclude that this demonstrates that a monetary policy that reacts only to output and inflation is insufficient, and that a (non-linear) response to asset prices, etc, is also desirable. They suggest this is inconsistent with inflation targeting. However, Bordo and Jeanne assume a standard loss function that is quadratic in the output gap and inflation. If one accepts the argument that an inflation target is really a statement about the objective function rather than the reaction function, a flexible inflation targeter would also choose their recommended policy. But their analysis does suggest that a richer interest rate reaction function may be required in the pursuance of that inflation target.
Financial instability and credit crunches are probably of the greatest significance when they adversely affect the supply potential of the economy. But even without such adverse supply effects, the unwinding of financial imbalances may cause problems for the design and conduct of monetary policy. In most settings, the appropriate response to the fall in aggregate demand occasioned by the unwinding of cumulative imbalances, triggered say by a fall in asset prices or a downward revision in expectations about future income or earnings, is simply to offset the shock to demand by lowering interest rates. But this may not be possible if the zero lower bound on nominal interest rates starts to bind. Although other monetary policy options may be available, including purchases of a broader range of assets than the central bank usually undertakes, as well as more exotic approaches such as taxing money balances à la Gesell (1958), their effectiveness is less certain than conventional interest rate policy. Consequently it will make sense to conduct a policy during the period of accumulating imbalances that reduces the likelihood of encountering the zero lower bound as the imbalances unwind.
Stochastic simulations with macroeconometric models suggest that, at an average inflation rate of 2 per cent, the fraction of time spent at the zero lower bound is likely to be around 2 per cent. And even for an average inflation rate of 1 per cent, the corresponding figure is only up to around 5 per cent (see the studies surveyed in Yates (2003)). That might appear to suggest this is not likely to be a very serious issue. But those stochastic simulations assume shocks similar to those experienced in the past. The unwinding of imbalances is likely to be sharp, particularly in the context of a credit crunch or similar financial instability, and so corresponds to shock realisations in the bottom tail of the distribution. That suggests the zero lower bound on interest rates provides a more compelling argument for pre-emptive action to prevent the build-up of imbalances in the first place.[8]
A second consideration arises from the fact that a sharp unwinding of imbalances is likely to make aggregate demand somewhat less predictable than normal. Knowledge of the current state of the economy is highly imperfect – unlike in the models above – and increased uncertainty about demand will inevitably be transmitted into greater variability in activity. Moreover the impact of interest rate changes on aggregate demand is also likely to become more uncertain in such an environment, especially if credit channel effects assume greater importance or if there is a credit crunch. Greater uncertainty about policy multipliers will then impact on the optimal policy setting, eg as in the seminal analysis of Brainard (1967).
In this case one would expect there to be something of a trade-off facing the policy-maker. Action taken today to reduce the build-up of imbalances might pay off in the longer term by reducing the future uncertainty that the policy-maker will face as the imbalances unwind. But, as before, that seems entirely consistent with the approach of flexible inflation targets, taken as a description of the objectives of policy rather than the route whereby they are achieved.
4. Identifying Imbalances: A Case Study
These considerations suggest that even inflation targeters – indeed especially inflation targeters – should take cognisance of the risks to future macroeconomic stability posed by cumulating financial imbalances and/or asset-price misalignments. No additional consideration of asset prices or financial imbalances need be introduced into the description of the objectives of policy beyond inflation and activity. But as it may be some while before imbalances unwind or misalignments correct, the policy-maker does need to look sufficiently far ahead in assessing the risks to the outlook posed by the build-up of imbalances and misalignments.
A key issue is, of course, the identification of threatening imbalances before they grow too large. But without the wisdom of hindsight, it is often hard to identify those that pose a real threat, as rapid debt accumulation or large asset-price movements may be a rational and justified response to a change in the economic environment. The empirical results of Borio and Lowe (2002), building on Kaminsky and Reinhart (1999), seek to develop indicators of imminent financial crises based on the joint behaviour of asset prices, credit and investment and using only information available to the policy-maker at the time. Such indicators will no doubt be a useful addition to the armoury of central banks, but early diagnosis of incipient imbalances is always likely to be difficult. By the time it is obvious that there is a problem, it may be too late to do much about it – at least with conventional macroeconomic tools – without causing the macroeconomic instability that the policy-maker wishes to avoid.
Moreover, as noted by a number of authors, the greater counter-inflationary credibility of monetary policy in the last decade or so itself complicates the identification of imbalances (see, e.g., Borio and Lowe (2002) or Goodfriend (2003)). Debt accumulation is likely to prove excessive if it is associated with unsustainably high levels of activity. When credibility was low, levels of activity above the natural rate tended to show up relatively quickly in accelerating inflation. But a feature of the last decade has been the apparent flattening of the short-run output-inflation trade-off (see Figure 1). There are at least three possible reasons for this. First, New Keynesian models of nominal price inertia relying on the presence of menu costs suggest that the slope of the output-inflation trade-off should be flatter at low average inflation rates (Ball, Mankiw and Romer 1988). Second, models of the Phillips curve in which expectations of inflation play a role – whether of the Friedman-Phelps-Lucas or New Keynesian varieties – suggest that an increase in activity above the natural rate will raise inflation less if those expectations are well anchored. Consequently the enhanced belief that monetary policy will be used to stabilise inflation will itself help to keep inflation low. Moreover, that credibility will also help to stabilise long-term interest rates. Third, increased competitive pressures in product markets, associated in particular with increased international trade, may also act to restrain inflationary pressures.
In such a world, excess debt accumulation and levels of demand above the natural rate will not immediately show up in higher inflation rates. Moreover, that in itself may encourage market participants and policy-makers to believe that the natural rate of output is higher than it really is. That in turn is likely to boost asset prices, further raising demand. Instead of showing up in inflation, the excess demand will show up in other indicators, such as profit rates, measures of labour shortage and the like. That suggests focusing attention on other indicators, as well as inflation, in identifying when demand is excessive and imbalances are unsustainable.
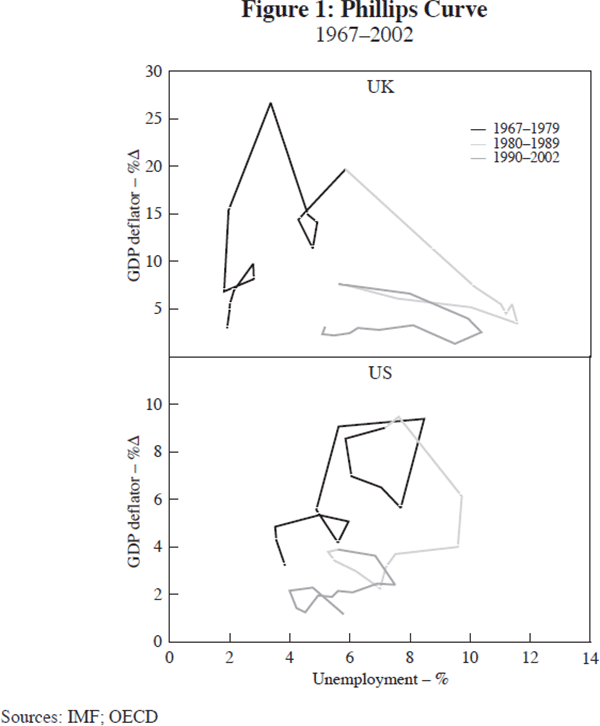
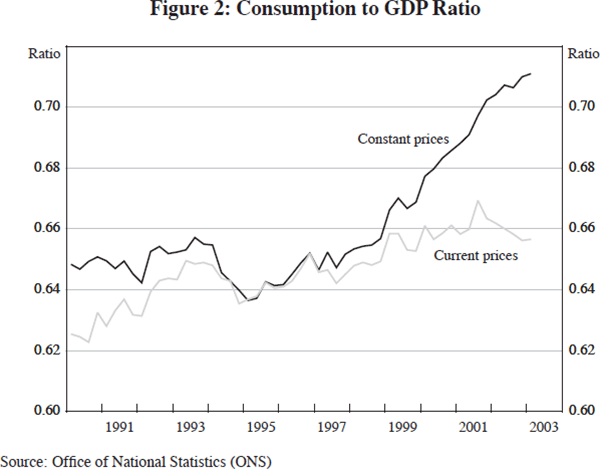
Rather than add to the body of work that seeks to develop early-warning indicators of potentially dangerous imbalances, I conclude with a review of current developments in the United Kingdom that illustrates the difficulties in assessing whether or not asset-price movements and credit growth constitute a potential problem. A key feature of the UK economy in the past six years has been the buoyancy of household spending which has consistently grown faster than output, in both real and nominal terms (see Figure 2). And associated with that has been a build-up of household debt and rapid house price inflation (see Figures 3 and 4). Moreover, the Bank of England's Monetary Policy Committee has over the past two years sought to offset the impact of the global slowdown by relaxing policy in order to further boost domestic spending, and in particular private consumption. That has added to the accumulation of household debt and raised house prices further. Is there any evidence that the financial imbalances in the household sector have reached the point where they might pose a threat to the economic outlook?
In addressing this question, it is helpful first to ask why consumer demand might have been so buoyant. Standard theory suggests that it should be ‘permanent’ income rather than current income that drives consumer spending, though the extent to which households will shift expenditure intertemporally will also depend on the cost of borrowing and the return to saving. The recent strong growth in consumption has coincided with robust growth in real disposable household incomes and falling unemployment, and for a while also with rising equity prices. So one explanation for the strength of consumer spending is that households have been revising up their assessment of their permanent income. To the extent that there has indeed been an increase in households' permanent income, then we would expect consumption growth in due course to fall back in line – or strictly speaking a little below – the rate of growth of their income, with the extra accumulated debt being gradually repaid. But if expectations prove to be over-optimistic then a sharper future correction to consumer spending is likely.
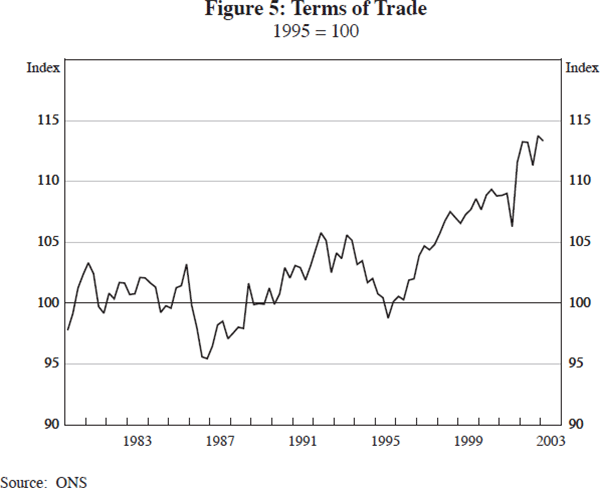
Furthermore, a significant fraction of the increase in real household incomes has been associated with the substantial improvement in the terms of trade – up 13 per cent since 1996 (see Figure 5). An important issue is whether the improvement from this source is permanent, reflecting the exploitation of comparative advantage, or whether it is associated instead with a temporarily high level of the exchange rate, in which case real incomes and consumption will eventually both drop back. The answer to this question is not obvious.
A second explanation for the rapid growth in consumer spending and debt is easier access to, or cheaper, borrowing. Here house prices enter the picture. The most important channel through which house prices affect consumer spending is probably not via a conventional wealth effect. Rather it is through increasing the value of the collateral against which owners – who would otherwise be credit-constrained – can borrow, or else by allowing them to borrow at lower rates. The higher house prices of recent years have allowed owner-occupiers to increase their borrowing, using the proceeds in part to boost spending. That is reflected in high rates of mortgage equity withdrawal, currently estimated to be equivalent to about 7 per cent of personal disposable income (see Figure 3).
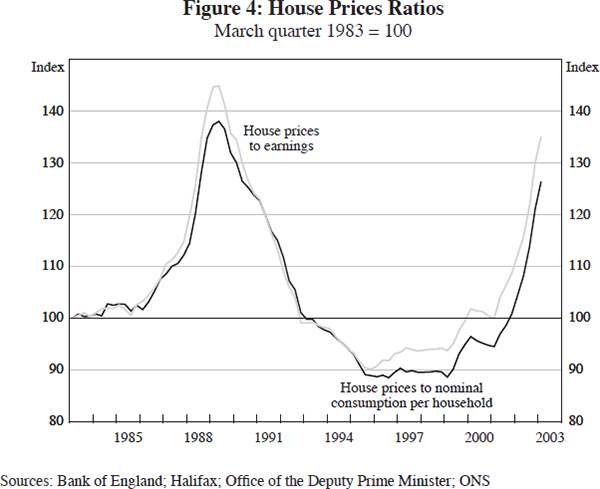
But why has the price of houses risen? The demand for housing services should be driven by the same factors that drive the demand for consumer goods and services, i.e., permanent income. Figure 4 also shows the evolution of house prices relative to the nominal value of consumer spending per household (a proxy for consumers' estimates of their permanent income). That ratio has risen sharply in recent years, although the picture is not quite as dramatic as when house prices are compared to earnings.
So something else has also been driving house prices, and with them the value of the collateral against which owner-occupiers can borrow. At first glance, Figure 4 might seem to indicate an incipient house-price bubble, but there are at least three reasons why the demand for housing might have risen more than might be suggested simply by looking at permanent income. First, the transition to a low-inflation environment implies that nominal interest rates should also be lower on average. As standard mortgages entail an even flow of nominal payments over the life of the mortgage, the initial real payments on a given nominal debt are smaller than they would be if inflation and interest rates were high, with the real burden of payments towards the end of the loan period being correspondingly greater. Shifting the pattern of real payments into the future in this way makes households that are constrained by their cash flow more willing or able to borrow, thus driving up the demand for housing. But a legitimate concern is that borrowers may not have fully factored in the corresponding increase in future real payments. Second, increased competition amongst lenders and the application of better credit scoring techniques may have increased the supply of loans. And third, population growth and demographic developments – more people wanting to live alone and an increased desire for second homes – will also have boosted demand.
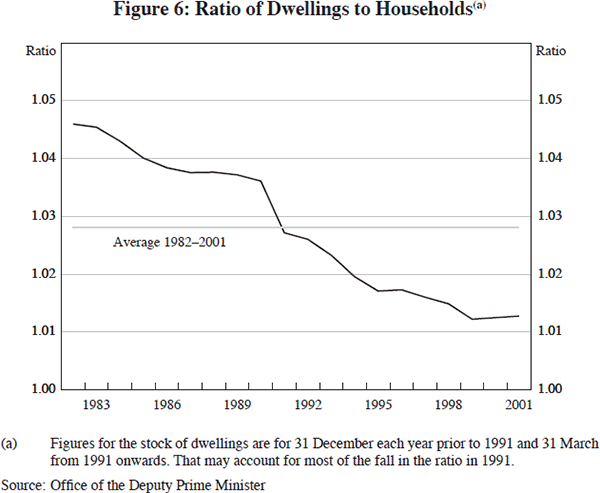
In addition, on the supply side of the market, the rate of construction of new dwellings in the United Kingdom has lagged behind the expansion in the number of households, in part because of a shortage of land and the impact of planning restrictions. Figure 6 shows that the ratio of dwellings to households – a measure of spare capacity in the housing market – has been steadily falling over the last two decades. One might reasonably expect that this might also be reflected in higher house prices relative to nominal consumption per household.
In sum, there are good reasons why a higher house-prices-to-consumption ratio (or house-prices-to-earnings ratio) might be warranted by underlying economic developments. But there is inevitably very considerable uncertainty about the underlying equilibrium value of house prices. An optimal monetary policy almost certainly would dictate a differential response to a movement in house prices associated with a misalignment to one that is associated with movements in the fundamentals. Yet diagnosing whether there is a misalignment is far from straightforward.
Whether the movement in house prices is justified by fundamentals or not is clearly also central to assessing whether there is any danger posed by the build-up of household debt that is the counterpart to the increase in the value of housing wealth. But even if a sharp correction were to occur to house prices, it would not necessarily imply a correspondingly sharp fall in household spending. Net household wealth would fall, but rational consumers would spread the required adjustment over the rest of their lives. Even consumers who were credit-constrained and had previously exploited the higher collateral to increase their borrowing would not need to cut back their spending sharply unless the lender were to foreclose on them for some reason.[9]
High levels of outstanding debt could, however, increase the impact on consumer spending of other adverse shocks to activity, especially those leading to higher unemployment. Households with adequate liquid assets, or who can still access the credit market, would not need to cut back their consumption much if they experience a spell of unemployment, assuming it does not harm their future earning potential. Instead they would simply run down their savings or borrow more. On the other hand, households with no assets, and who cannot borrow, would be forced to cut back spending in line with their reduced income. So the impact of this adverse shock on aggregate consumption will be greater, the higher is the fraction of constrained households. Furthermore that fraction will tend to be higher, the greater is the amount of debt already extended.
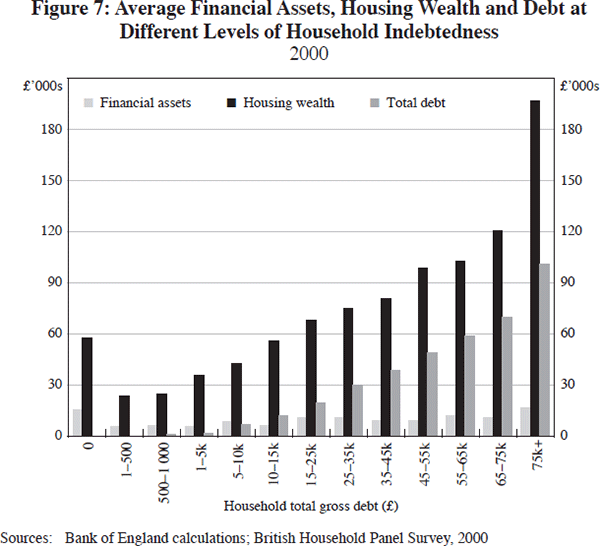
So a key question is whether those who hold the debt are particularly likely to be exposed to adverse shocks, such as job loss, and whether they have other assets that they could run down. The good news is that it is those households who hold the most debt who also tend to have higher income and more assets (see Figure 7). But this is not very surprising as most of the debt is in the form of mortgages and bigger mortgages are typically associated with more expensive houses!
Perhaps more relevant in assessing the potential vulnerability of the household sector to shocks is the matching of debts to liquid assets. Here the news is not quite so good. Figure 8 illustrates the distribution of total liabilities and liquid assets across individual households, drawn from a 10 per cent random sample of the 5,000 households in the 2000 British Household Panel Survey (BHPS). It is notable that a large fraction of households are positioned on one or other axis. In particular, roughly a third had no liquid assets to speak of. This suggests that the financial position of the household sector might be rather less resilient than is suggested merely by looking at aggregate balance sheet data.
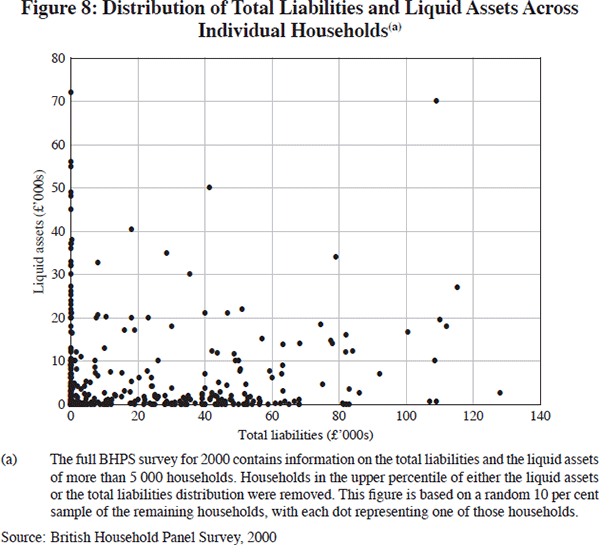
This example illustrates the problems that confront policy-makers in assessing whether strong credit growth and asset-price appreciation are merely the consequence of movements in underlying economic fundamentals or represent something more dangerous. Moreover, even if it is the latter, aggregate data may need to be supplemented by microeconomic information in order to evaluate in full the possible problems caused by their unwinding.
5. Concluding Remarks
Financial imbalances, asset-price misalignments and the instability that may result as they correct may pose significant problems for monetary policy-makers. Achieving price stability is no guarantee that financial instability can be avoided. But taking account of financial imbalances in the design of monetary policy does not require a change in the formal structure of inflation targets. Significant financial instability invariably will also have a significant impact on activity and inflation. The attraction of inflation targets is that they focus on the goals of policy – not the means by which they are achieved, as is the case under regimes such as money supply targets and fixed exchange rates. An inflation-targeting regime comprising a ‘first-level’ target for the inflation rate together with a subsidiary objective of stabilising activity is a practical solution to the problem of describing the principal's objective function. A flexible inflation targeter – in the specific sense of Svensson – does not then require the explicit addition of financial imbalances or asset prices to be added to their remit. Rather the implications of possible imbalances and misalignments for the macroeconomic goal variables must necessarily be factored into the assessment of expectations of future growth and inflation in order to execute the optimal plan. So the answer to the question posed in the title of this paper is: Yes, (flexible) inflation targets are enough. But taking on board the possible risks posed by cumulating financial imbalances may require a shift in the rhetoric of inflation targeters towards the longer term.
More investigation is, however, needed into understanding the way in which financial imbalances and asset-price misalignments in practice affect economic prospects. There are at least two distinct sets of issues where further work would be useful. First, it would be helpful to advance our ability to detect when rapid credit expansion and asset-price increases are symptomatic of the development of underlying imbalances that are susceptible to future correction, rather than simply reflecting sustainable movements in the underlying economic fundamentals. Second, improving our understanding of how imbalances unwind and their associated costs would facilitate the design of appropriate policies, on both the monetary and regulatory front. It is safe to assume that these two issues will remain on the agenda for both monetary economists and central bankers for many years to come.
Appendix
There are two types of agents in the economy: households and firms. Households are infinitely lived, supply labour, consume and can borrow and lend freely. All debt lasts a single period and is denominated in real terms. Households also own a non-tradable diversified portfolio of shares in firms, so that all profits are returned to households in lump-sum form. Firms are monopolistic competitors, and nominal prices are fixed with a fraction of prices being reset each period as in the standard New Keynesian Phillips curve. Capital lasts a single period, has to be installed a period in advance, and is financed entirely by borrowing from households.
Credit crunches occur with a fixed probability, ρ. When they do occur their effect is to lower the level of supply in the economy. In effect a credit crunch is a negative shock to total factor productivity, though it reflects events in financial markets rather than a change in the technical capabilities of the economy. If a credit crunch does occur, it is assumed to be more severe the higher is the level of overall debt outstanding. An individual firm's borrowing decision has a negligible impact on overall debt. Consequently firms ignore the impact of their borrowing on the severity of any future credit crunch, i.e. there is a negative externality present.
The production function is Cobb-Douglas in capital and labour:

where yt is (the logarithm of) output in period t, at is (the logarithm of) total factor productivity in period t, kt is (the logarithm of) the capital stock at the start of period t, inherited from the previous period and nt is (the logarithm of) employment in period t. Total factor productivity is given by the process:

where et is a shock to the technology, dt is the (logarithm of) debt outstanding and εt is an indicator variable that takes the value unity if a credit crunch occurs and zero otherwise. The severity of the credit crunch thus depends on the debt-to-(expected)-output ratio. We write (A2) in terms of expected output rather than realised output because the latter depends on whether a credit crunch occurs or not; writing the credit crunch in terms of realised output complicates the analysis considerably.
Equation (A1) may be inverted to give labour demand conditional on the level of output:

The demand for capital is then obtained by minimising expected costs, conditional on the expected future level of output and recognising that employment will subsequently be determined through the labour requirement Equation (A3):
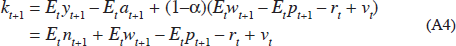
where wt is (the logarithm of) the nominal wage in period t, pt is (the logarithm of) the price level in period t, rt is the real rate of return on debt and vt can be thought of as representing a shock to ‘animal spirits’, i.e. irrationally over-or under-optimistic expectations. For simplicity, vt is assumed to be serially uncorrelated, and inessential constants are normalised to zero through appropriate choice of units throughout.
Following Calvo (1983), prices are set on a staggered basis, with those firms that are able to change their price choosing an optimal one based on expected marginal cost.

where mt (= wt – pt + nt – yt) is (the logarithm of) marginal cost and ut is an uncorrelated shock to the mark-up.
Turning to the household sector, savings are assumed to be a constant fraction of income, and labour supply is an increasing function of the real wage alone:

The model can be developed along standard lines with an inter-temporal optimality equation for consumption and a corresponding intra-temporal optimality condition for labour supply, but that merely complicates the dynamics without changing the basic insights.
Given the constant savings rate assumption, an IS schedule can then be obtained from (A4) and using the equality of marginal cost and the labour share:

This is similar to the standard New Keynesian IS curve, save for the appearance of expected marginal cost.
Using Equations (A3) and (A6), marginal cost is:
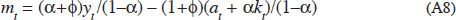
The flexible price level of output, yot, is then obtained by setting mt = 0:

where ν = (1+φ)/(a+φ). The model may then be condensed into the two equations:

where xt (= yt − y°t) is the output gap and κ = δ(α+φ)/(1−α), and:

where r°t = Et y°t+1 − y°t is the natural real rate of interest and η = (1+φ)/(1−φ)(=κν/δ).
The policy-maker seeks to stabilise output around its technically feasible level:

When there is no credit crunch, this is just the same as the flexible price equilibrium, yot. But when a credit crunch occurs, there will be a gap between the two, which is larger the greater is the current debt-output ratio. Using the fact that dt = kt + rt-1, the relevant gap, x*t is:
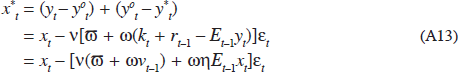
Consider first the optimal policy under discretion. Under discretion, the central
bank is forced to treat private sector expectations as exogenous and unaffected
by its current policy choice in carrying out the optimisation; let 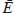 denote such a private sector expectation. The Lagrangian
for the optimisation problem for the central bank at date τ may then
be written:
denote such a private sector expectation. The Lagrangian
for the optimisation problem for the central bank at date τ may then
be written:
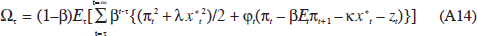
where 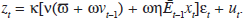 The first-order conditions are, for all t>
x:
The first-order conditions are, for all t>
x:

Eliminating the multiplier gives:

This is essentially the same as Equation (6), but written in terms of the deviation of output from its technically feasible level, rather than the flexible price equilibrium.
Now consider the optimal policy when the central bank is able to pre-commit, in which case it will take account of how private sector expectations will be affected by its choice of policy. First note that Equation (A13) implies that:
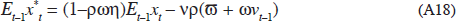
Using this, the Lagrangian for the central bank's optimisation problem at date τ may be written:
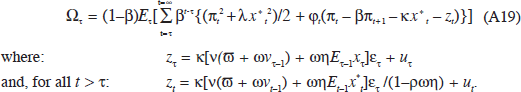
The first-order conditions are then:
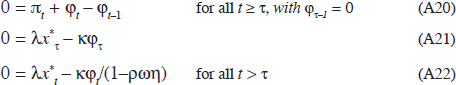
These equations describe a ‘τ-optimal’ equilibrium, reflecting the fact that expectations formed prior to date τ are treated as bygones. As noted by Svensson and Woodford (2003), it would not be optimal to stick to this plan for dates after τ, i.e. it is time inconsistent. But if the authorities can pre-commit, it makes sense to consider not the ‘τ-optimal’ solution, but rather a ‘timelessly optimal’ plan in which the optimisation is assumed to occur arbitrarily far in the past and so is independent of initial conditions. In that case, the initial condition φτ–1=0 and the first-order condition (A21) that treats Eτ–1xτ in zτ as a bygone are both irrelevant, and the optimum is effectively characterised by (A20) and (A22). Combining these by eliminating the multipliers then gives a set of optimality conditions analogous to Equation (7) that applies for all decision dates τ:
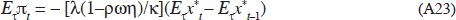
Footnotes
Chief Economist and Member of the Monetary Policy Committee, Bank of England. I am grateful to Peter Andrews, Francesco Giavazzi, Ed Nelson, Ignazio Visco and Sushil Wadhwani and participants of the conference on ‘Monetary Stability, Financial Stability and the Business Cycle’ at the Bank for International Settlements, Basel, 28–29 March 2003 for useful comments. The views expressed are those of the author and do not reflect those of either the Bank of England or the Monetary Policy Committee. [1]
To see this just set k=0, which gives Πt = – (λ/κ)(xt – xt–1). [2]
If the objective function contains a term in the interest rate, as in Woodford (1999), then the policy instrument appears in the optimality condition. It is then, however, a rather different animal from the instrument rules (1) and (2). [3]
In an open economy subtle issues arise as to whether the real exchange rate should also appear in the optimality condition as a result of the impact of the terms of trade on consumer prices. Under some assumptions, the closed economy model of the text can be translated directly into an open economy setting (see e.g. Clarida, Galí and Gertler (2001)), but under other formulations that is not necessarily the case. However, it is clear that the presence of the real exchange rate in the optimality condition under such circumstances has little to do with arguments about the appropriate response to asset price bubbles. [4]
The Chancellor has recently announced his intention to switch the targeted measure to the Harmonised Index of Consumer Prices (HICP) at a future date. [5]
Recall that the constant savings rate assumption implies that higher output must be associated with higher capital formation and therefore more debt accumulation. [6]
This channel is absent in the model described in this paper because of the assumption that the semi-elasticity of debt with respect to the interest rate is unity. [7]
Note that this argument suggests that greater uncertainty may lead to greater policy activism, in contrast to the classic Brainard (1967) result. [8]
Note that the mere fact that the value of the collateral is less than the value of the loan does not necessarily imply the borrower will choose to walk away from the debt and forfeit the asset. Some borrowers may, for reputational reasons, prefer to repay their debts even though they are worth more than the value of the collateralised asset. Hence lenders, having extended the loan on the basis of what turns out to be a temporarily inflated collateral value, may prefer not to foreclose. [9]
References
Ball L, NG Mankiw and D Romer (1988), ‘The New Keynesian economics and the output-inflation trade-off’, Brookings Papers on Economic Activity, 1, pp 1–65.
Batini N and E Nelson (2000), ‘When the bubble bursts: monetary policy rules and foreign exchange market behaviour’, Bank of England, mimeo.
Bean CR (1998), ‘The new UK monetary arrangements: a view from the literature’, Economic Journal, 108(451), pp 1795–1809.
Bernanke BS and M Gertler (2000), ‘Monetary policy and asset price volatility’, in New challenges for monetary policy: a symposium sponsored by the Federal Reserve Bank of Kansas City, Federal Reserve Bank of Kansas City, Kansas City, pp 77–128.
Bernanke BS and M Gertler (2001), ‘Should central banks respond to movements in asset prices?’, American Economic Review, 91(2), pp 253–257.
Bordo MD and O Jeanne (2002), ‘Boom-busts in asset prices, economic instability, and monetary policy’, NBER Working Paper No 8966.
Borio C and P Lowe (2002), ‘Asset prices, financial and monetary stability: exploring the nexus’, BIS Working Paper No 114.
Brainard W (1967), ‘Uncertainty and the effectiveness of policy’, American Economic Review, Papers and Proceedings, 57(2), pp 411–425.
Calvo GA (1983), ‘Staggered prices in a utility-maximum framework’, Journal of Monetary Economics, 12(3), pp 383–398.
Cecchetti SG, H Genberg, J Lipsky and S Wadhwani (2000), Asset prices and central bank policy, Geneva Reports on the World Economy No 2, International Center for Monetary and Banking Studies and Centre for Economic Policy Research, Geneva.
Cecchetti SG, H Genberg and S Wadhwani (2003), ‘Asset prices in a flexible inflation targeting framework’, in WC Hunter, GG Kaufman and M Pomerleano (eds), Asset price bubbles: the implications for monetary, regulatory, and international policies, MIT Press, Cambridge, Mass, pp 427–444.
Clarida R, J Galí and M Gertler (2001), ‘Optimal monetary policy in open versus closed economies: an integrated approach’, American Economic Review, 91(2), pp 248–252.
Crockett A (2003), ‘International standard setting in financial supervision’, Institute of Economic Affairs Lecture, Cass Business School, London, 5 February.
Gesell S (1958), The natural economic order, Peter Owen Ltd, London.
Giannoni MP and M Woodford (2002), ‘Optimal interest-rate rules: II. Applications’, Princeton University, mimeo.
Goodfriend M (2003), ‘Interest rate policy should not react directly to asset prices’, in WC Hunter, GG Kaufman and M Pomerleano (eds), Asset price bubbles: the implications for monetary, regulatory, and international policies', MIT Press, Cambridge, Mass, pp 445–457.
Greenspan A (2002), ‘Economic volatility’, remarks at a symposium sponsored by the Federal Reserve Bank of Kansas City, Jackson Hole, 28–30 August.
Groth C (2003), ‘Monetary policy and asset price fluctuations’, paper presented to the European Economic Association Conference, Stockholm, 20–24 August.
Kaminsky GL and C Reinhart (1999), ‘The twin crises: the causes of banking and balance-of-payments problems’, American Economic Review, 89(3), pp 473–500.
King MA (1997), ‘The inflation target five years on’, Bank of England Quarterly Bulletin, 37(4), pp 434–442.
Kiyotaki N and JH Moore (1997), ‘Credit cycles’, Journal of Political Economy, 105(2), pp 211–248.
Miller M, P Weller and L Zhang (2002), ‘Moral hazard and the US stock market: analysing the “Greenspan put”’, Economic Journal, 112(478), pp C171–C186.
Stock JH and MW Watson (2001), ‘Forecasting output and inflation: the role of asset prices’, NBER Working Paper No 8180.
Svensson L (2001), ‘Requiem for forecast-based instrument rules’, Institute for International Economic Studies, Stockholm University, mimeo.
Svensson L (2002), ‘What is wrong with Taylor rules? Using judgment in monetary policy through targeting rules’, Princeton University, mimeo.
Svensson L and M Woodford (2003), ‘Implementing optimal policy through inflation-forecast targeting’, NBER Working Paper No 9747.
Taylor JB (2001), ‘The role of the exchange rate in monetary-policy rules’, American Economic Review, 91(2), pp 263–267.
Woodford M (1999), ‘Optimal monetary policy inertia’, NBER Working Paper No 7261.
Yates A (2003), ‘Monetary policy and the zero bound to nominal interest rates’, Bank of England Quarterly Bulletin, 43(1), pp 27–37.