RBA Annual Conference – 2003 What the FOMC Says and Does When the Stock Market Booms Stephen G Cecchetti[1]
Abstract
Central bankers and monetary economists continue to debate the wisdom of adjusting policy in reaction to asset-price misalignments or bubbles. Experts on both sides have marshalled theoretical and practical arguments, but failed to achieve consensus. In this paper, I first summarise the argument in favour of interest rate reactions to equity-price misalignments, and then provide evidence that Federal Reserve words and actions were influenced by the Internet bubble as it was in progress. That is, I show that as equity prices boomed, members of the Fed's policy-making body, the Federal Reserve's Open Market Committee (FOMC), spoke more intensively about the stock market, and adjusted interest rates accordingly. The debate should not be about whether they should have reacted, but whether they did enough.
1. Introduction
From August 1997 to June 1999 I sat on the backbench at the meetings of the FOMC and received all of the material distributed to the participants. Prior to each of these meetings a number of things were distributed to meeting participants, including a set of economic forecasts. Prepared by the Division of Research and Statistics at the Federal Reserve Board, these forecasts were contained in what is known as the ‘Green Book’. The Green Book would arrive in my office on Thursday afternoon prior to the coming Tuesday meeting. Before that, on Thursday morning, the Deputy Secretary of the FOMC Normand Bernard would convene a conference call with representatives from all twelve Federal Reserve Banks. The primary purpose of this call was to describe the assumptions that went into the Green Book forecasts. These assumptions were about things like oil prices, exchange rates, and the stock market, were not written down in the Green Book itself, and as far as I know are not readily available. The interesting thing is that during the period when I took part in this process, the Board staff preparing the forecasts invariably assumed that the US stock market would decline significantly – 10 to 20 per cent declines in the Wilshire 5,000 index were commonly the basis for the forecasts.[2] They clearly believed that the stock market was overvalued.
While we can argue over whether it made sense to forecast a decline in the American equity markets in 1998, the need for a forecast is not debatable. The future path of consumption depends on wealth, and stocks are a significant component of wealth. Without a forecast of consumption, there is no way to forecast GDP. And inflation forecasts depend on the forecasts of the output gap, which themselves depend on these GDP forecasts. Central bankers have no choice; to do their job they must forecast the stock market. And during the boom of the late 1990s, FOMC actions were based at least in part on forecasts that were built on an assumed decline in equity prices.
At the time this was all happening, I confess that I was scandalised. I regularly ranted about the practice of forecasting a dramatic decline in the stock market. Like the vast majority of academics, I adhered to the efficient markets view. How could the Board staff forecast a stock market decline? Hadn't they read any of the thousands of papers showing that stock market movements aren't predictable? Yes, there are anomalies at the level of individual stocks, but in the aggregate, the market looks very efficient. So while we needed to assume something about the stock market, shouldn't we assume the equity index would stay constant at its current level indefinitely? After all, if we were so smart why weren't we rich?
This happened five years ago (which is why I can talk about it now), and in the interim I have changed many of my views.[3] I have a new appreciation for what the Board staff was doing – what they had to do – and have been working to understand the consequences of my changed view for how policy-makers should go about their jobs.
All of this is by way of introducing this paper and the question ‘what the FOMC says and does as the stock market booms’. While the material distributed to the attendees in 1998 clearly had buried in it assumptions that the stock market would decline, did those concerns find their way into the discussions at the meeting itself? Even if it did, as economists like to say, talk is cheap. We are more interested in what people do than what they say, and that brings us to interest rate actions. Did the federal funds rate target move in reaction to the stock market? These are the questions that I hope to answer.
The remainder of this paper is divided into two parts. In the first, contained in Sections 2 and 3, I provide a brief summary of the debate over the role that asset prices should play in interest rate setting and regulatory policy. I do not pretend that my synopsis is either balanced or exhaustive. Instead, I take this opportunity to react to those who have criticised my earlier writings. In Sections 4 and 5, I shift from a normative discussion of what the FOMC should have done to a positive examination of what they actually did. This new empirical work first looks at what FOMC members said at their meetings. In Section 4, I report that the frequency with which the FOMC discussed the stock market increased as the market climbed in the 1990s. Section 5 moves on to what the FOMC did. Here I report estimates of a policy reaction function that suggests the federal funds rate was moving in response to a measure of equity-price misalignments. Overall I conclude that when they met, the FOMC talked about the stock market, and when they set policy, they reacted to misalignments.
2. Should Interest Rates Respond to Asset Prices? The State of the Debate
Nearly everyone agrees that asset-price bubbles are bad and that we would all be better off without them. Abrupt changes in asset prices affect virtually every aspect of economic activity. Wealth effects cause consumption to expand rapidly and then collapse. Increases in equity prices make it easier for firms to finance new projects, causing investment to boom and then bust. The collateral used to back loans is overvalued, so when prices collapse it impairs the balance sheets of financial intermediaries that did the lending.
Over the last few years we have seen even more unpleasant consequences of the recent stock market bubble. Pension funds, booking the high returns of the 1990s, were unprepared for the collapse and are now underfunded.[4] Insurance company reserves are too low. And, most importantly, government finances have been distorted. As equity prices rose, capital gains tax revenue went up with them. This increased government revenue, which led to both increased expenditure and reduced taxes. With the bursting of the bubble, tax revenues have fallen dramatically. In the current political environment, it is impossible to raise taxes, and so the result is a combination of expenditure cuts and increased borrowing.
Another, more subtle, difficulty comes from the fact that higher investment during the boom both drove up observed real growth and raised the apparent productive capacity of the economy, further confusing permanent from cyclical movements in output. The problem is that some portion of the investment during the boom should not have been undertaken. That is, if prices had been correct these projects would not have had positive internal rates of return. When prices fell, many of these investments were abandoned – we all recall the pictures of warehouses piled high with discarded computer equipment. This makes potential GDP look higher than it actually is. For policy-makers this creates the risk of trying to stabilise growth at too high a level. For the rest of us it means overly optimistic expectations about growth of income and consumption.
The evidence is not in dispute. Bubbles increase the volatility of growth, inflation, and threaten the stability of the financial system. The 2003 IMF World Economic Outlook estimates that the average equity-price bust lasts for 2½ years and is associated with a 4 per cent GDP loss that affects both consumption and investment.[5] It is the job of central bankers to eliminate the sort of economic distress caused by asset-price bubbles. The idea that they should ignore them seems absurd on its face. But what should they do?
Over the past few years a large number of papers have addressed this question both from a theoretical and practical viewpoint. There are now so many papers that examine the connection between asset prices and monetary policy that it would be foolhardy for me to try to summarise them here. I will instead identify three views. The first is the Bernanke and Gertler (2000, 2001) conclusion that central bankers should respond to asset prices only in so far as they affect forecasts of future inflation. Related to this is the view put forth by Mishkin and White (2002) and Schwartz (2002), both of whom suggest that asset-price bubbles should only be a concern when they affect the stability of the financial system. And finally, in my previous work, I have explained why I believe that the best way for policy-makers to temper the impact of bubbles on inflation and growth is to adjust interest rates in response to asset-price misalignments.[6]
To be absolutely as clear as possible, my previous co-authors and I agree that policy-makers should not target asset prices, and we have said so repeatedly. Let me quote from Cecchetti et al (2003, p 428):
It is our view that central banks can improve macroeconomic performance by reacting to asset price misalignments. We are not now saying, nor have we ever said, that policymakers should target asset prices. [Emphasis is in original.]
The debate is explicitly not about central bank objectives. It is about how to go about achieving whatever combination of price and output stability policy-makers are aiming to deliver. The proposal that interest rates respond to bubbles is completely consistent with inflation targeting or any other policy framework based on standard stabilisation objectives.[7]
There is a growing body of literature supporting the idea that asset prices have a place in monetary policy rules. Dupor (2002) builds a model with sticky prices in which firms over-invest in physical capital when stocks become overvalued. The optimal monetary policy reaction in the Dupor model is to raise interest rates to drive down employment, driving down the marginal product of capital, thereby reducing its price. Gilchrist and Leahy (2002) come to a similar conclusion when considering the consequences of a shock to the net worth of entrepreneurs.[8] In their set-up a rise in net worth reduces the risk premium on loans, creating investment increases that are unwarranted by long-run economic fundamentals. Raising interest rates will reduce this distortion and stabilise the economy in the long run.
It is fair to say that the conclusion that asset prices should appear in monetary policy rules is not robust. One example is the paper by Gruen, Plumb and Stone (this volume). In a series of simulation experiments they compare responses to large and small asset-price bubbles and find that an ‘activist’ policy-maker determined to respond to a bubble may want a looser policy than a sceptic when the bubble is large. Since it is large bubbles that we really care about, their conclusion is that we are better off not doing anything explicit about it.
Many people have attacked the view that monetary policy should react to deviations of asset prices from their fundamental values. Borio and Lowe (2002) provide a nice summary of the three arguments against using interest rates to combat the instability caused by bubbles. They are:
- The difficulty authorities have in identifying imbalances in a timely and precise fashion.
- The risk that policy responses will compound the problem.
- The difficulty in justifying the action to the public.
Let's consider each one of these in turn.
The most common criticism of the activist view is that central bankers aren't going to be able to identify bubbles when financial markets can't. My previous response to this criticism is that just because something is hard to measure is no reason to ignore it. Cecchetti et al (2003) argue that it is surely no more difficult to measure asset-price misalignments than it is to estimate potential GDP, and that there are surely times when asset prices are obviously misaligned.
The criticism of this view is based on the efficient markets logic that markets incorporate all available information and this automatically eliminates bubbles. But there are many circumstances under which the argument fails. The dynamic stories that we tell to explain market efficiency are based on the arbitrage. And when arbitrage fails, so does market efficiency. In fact, even if everyone knows that there is a bubble, there is a broad set of realistic circumstances under which arbitrageurs will not eliminate it.
In a recent paper, Stein (2003) constructs just such a model. He starts from the realistic premise that we cannot identify good from bad money managers. In order to signal that they are good and overcome the information asymmetry, a manager must allow redemptions from the fund being managed – that is, the fund has to be open-ended rather than closed-end. And an open-ended fund is exposed to withdrawal if it underperforms its benchmark. That is, investors will monitor short-run performance and take their money out of a fund that underperforms because that is evidence that the manager may be bad.[9]
To understand the importance of this line of reasoning, consider a bubble in the aggregate equity market that is certain to eventually burst. Specifically, imagine that the bubble grows at 5 per cent each quarter, and has a 5 per cent probability of bursting each quarter. The existence of the bubble is common knowledge among the well-informed fund managers, but their naïve investors aren't sure about it. Will the manager of an open-ended fund take a short position to profit from the bubble? The answer is almost surely no. With the bubble growing each quarter, a manager that is long will have a 5 per cent return every quarter until the bubble bursts. Alternatively, if the manager sells the market short, the fund will lose 5 per cent every quarter until the bubble bursts.[10] Since the fund is open-ended and investors worry about manager quality, they will withdraw their money from the fund that sells short. In equilibrium, no-one sells short, everyone goes long, and the benchmark against which performance is judged is the bubble return, and arbitrage doesn't drive prices to fundamentals even though everyone knows the bubble is there.
It is natural to ask why hedge funds can't profit from this. Hedge fund managers have significant access to leverage, few restrictions on their investment strategy, and appear to severely restrict withdrawals. While all this may be true, the fact is that the vast majority of hedge funds look for trades that converge rapidly. And performance is evaluated at least quarterly. Unfortunately, there is no survey of hedge fund withdrawal policies, but anecdotal evidence suggests that they are structured essentially as open-ended funds. Large investors can negotiate with the manager to allow for frequent withdrawals in the event of underperformance. While we don't know as much about this as we would like, casual observation suggests that the hedge funds are out there taking short positions that would have to be in place for several years before they pay off.
What about the risk that interest rate actions will destabilise the economy? The problem with this argument is that estimates of the impact of policy actions on the economy are extremely imprecise under normal circumstances. While we have rules of thumb for how much an interest rate change will affect growth and inflation after one or two years, the statistical basis for these is relatively weak. The precision with which we can estimate the impact of policy changes on central bank objectives is very poor. While this imprecision naturally brings caution, it should not lead to paralysis. An equity-price bubble should be viewed as just another shock.
Finally, there is communication. It is always difficult to explain interest rate hikes. And the normal explanation is that policy adjustments are necessary to stabilise prices and growth in medium term. That explanation will surely work here as well.[11]
Mishkin and White (2002) argue against an overly intense focus on asset prices, concluding instead that central bank policy should focus on financial stability per se. To the extent that asset-price bubbles materially affect the balance sheet positions of financial firms, there should be a reaction. But if balance sheets are strong, and the financial system is able to withstand being whipsawed by asset-price booms and busts, then policy-makers should simply sit by and watch. Central bankers should, however, respond to disruptions in financial markets. Mishkin and White refer to approving lender-of-last-resort operations such as the Federal Reserve's injection of over US$100 billion of reserves into the banking system after September 11, 2001.
It is difficult to disagree with the Mishkin and White view as a prescription for policy after the fact. Whenever the financial system is at risk, it is incumbent on central bankers to act. The real question is what they should do before we get to that point. And here, interest rate policy is one option. Another is to adjust regulations in order to minimise the potential for damage. I take up that issue next.
3. Regulation vs Monetary Policy Reponses
Once monetary economists realised that high and stable real growth required a stable financial system, they became interested in financial regulation. The work of the past decade or so has led to a new understanding of the interactions between the financial system and real economy, and specifically how to design a banking system that will support growth. This new view is evident in the proposed reforms to the Basel Capital Accord, Basel II.
An important concern of those designing the financial regulatory framework is that regulations themselves not exacerbate business cycle fluctuations. The potential for this arises from the way in which traditional capital requirements function. To see what can happen, consider the consequences of a broad economic slowdown. As the economy slips into recession, borrowers become less able to repay loans, and so defaults increase. Defaults mean a reduction in the value of bank assets. Unless the bank can raise additional capital, this leads immediately to shrinkage in the quantity of loans the bank is able to make. Reduced bank lending further slows economic activity, making the recession worse. Capital requirements themselves become pro-cyclical.
Borio, Furfine and Lowe (2001) provide a detailed description of this mechanism, and go on to suggest a set of policy options including the implementation of cyclically sensitive capital requirements. That is, raising capital requirements in booms, and reducing them in recessions. The recent episode in the US suggests that bank risk management practices may cause this to happen naturally. During the boom of the late 1990s, banks increased their capital to levels well in excess of the regulatory minimum and so have not been forced to contract in the aftermath of the bursting of the bubble.
Schwartz (2002) suggests a similar solution to the problem posed by asset-price bubbles. Again focusing on the ensuring financial system stability, she proposes that capital requirements be made sensitive to the extent to which assets whose prices have recently risen collateralise loans. In the words of Federal Reserve Board Governor Ben Bernanke (2002) ‘the Fed should use monetary policy to target the economy … [and] use its regulatory, supervisory, and lender-of-last resort powers to protect and defend the financial system’. And it is the danger to the financial system that is at the core of the difficulties caused by asset-price bubbles.
In evaluating these proposals, we need to ask whether it is practical to adjust capital requirements in the manner proposed. Adopting the suggestion of Borio et al would mean indexing capital requirements to something like the output gap. The Schwartz recommendation means indexing the capital requirements to something like inflation in equity and housing prices. The political power of the bankers being regulated means that they would have to agree to the indexing provisions. It is difficult to see bankers and regulators agreeing on how to compute such indices or on the formula to implement the adjustments in a way that would accomplish the desired goals. At a minimum, it would politicise the computation of the output gap and asset-price index used as an input into the formula. In the end, I don't see how this can succeed.
Hardouvelis and Theodossiou (2002) and Hardouvelis (2003) argue for using a different regulatory tool to protect the system from asset-price booms and busts. Instead of tempering the actions of the lenders, they suggest going after a particular group of borrowers, those who use margin loans to purchase equity. They present evidence that increases in margin requirement during booms help to reduce both mean reversion and volatility in equity markets, helping to reduce mispricing. The suggestion is that regulators implement a margin policy that raises requirements as the market goes up, and eases them as it goes down.
There have been a number of criticisms levelled at this suggestion. First, there is the fact that margin loans account for only 1 to 2 per cent of total stock market capitalisation. Second, people have argued that sophisticated traders can always go into derivatives markets if what they want is leverage. And finally, there is the claim that the data do not support the conclusion. Hardouvelis (2003) takes on all of these criticisms. First, size really isn't everything. While margin accounts may be small, that doesn't mean they aren't important.[12] Margin trading accounts for approximately 20 per cent of total trading in US equity markets. Second, as I have already argued there seem to be serious barriers to certain forms of arbitrage that would also make it difficult for investors to take the derivative positions that replicate leveraged long positions in the equity market. And finally, critics of the empirical claims simply conclude that margin requirements don't matter. As Hardouvelis emphasises, just because a policy instrument may be ineffective is no reason to give up on using it.
These ideas have tremendous appeal. Authorities should use regulatory tools to address stock price misalignments, leaving interest rates to pursue more traditional policy goals. Over the past decade, however, the regulators have not taken this route. I know of no country in which capital requirements have been adjusted in the manner suggested. And in the US, at least, margin requirements have been completely ignored. While technicians might be able to agree that such policies should be tried, I suspect that the political difficulties in implementing them would be insurmountable.
That does not mean that the authorities should do nothing. Another option, explored in Cecchetti and Li (2003), is for monetary policy to react to the health of bank balance sheets. That is, central banks can use interest rate policy to neutralise the procyclical effects of capital requirements by taking explicit account of the impact capital requirements have on bank balance sheets in the policy reaction function. That is, if policy-makers ease interest rates as banking system balance sheets deteriorate, they can eliminate the procyclical impact of capital requirements.
Throughout most of the period of the Internet bubble, Federal Reserve officials were remarkably silent about the stock market. Perhaps chastened by the reaction to Chairman Greenspan's December 5, 1996 statement about the financial markets ‘irrational exuberance’, policy-makers consistently refused to discuss equity prices in public. But as I suggested in the introduction, this does not mean that they were ignoring them. Did public silence imply private indifference? Or were officials both discussing and reacting to the asset-price bubble and its impact on the banking system? What was the FOMC saying and what were committee members doing? An empirical analysis of this question is the subject of the remainder of this paper.
4. What Was the FOMC Saying?
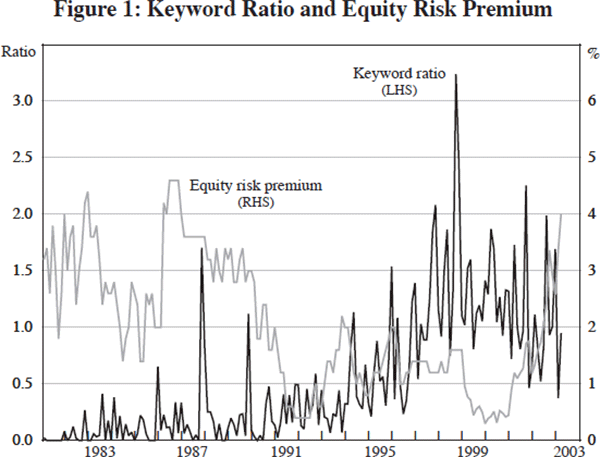
While they might publicly deny that they are paying much attention to equity markets, it is interesting to look at what FOMC members were actually talking about at their meetings. To do this, I examined FOMC minutes and transcripts beginning in 1981 looking for a set of keywords. The procedure involved simply counting the number of occurrences of a set of words, not reading statements and evaluating content. For each transcript from 1981 to 1997, and each set of minutes since then, I looked for the following words: asset, equity, equities, stock, stock market, securities, investment, financial market, index, index prices, S&P, Dow Jones, NYSE, bubble, and exuberance.[13] In order to account for things like the fact that FOMC meets for two half days twice a year (in February and June) and one half day six times a year, I measured the occurrences as a proportion of the total number of words in each document. And to adjust for the fact that minutes are qualitatively different from transcripts, I used an overlapping year to estimate a simple regression of transcript on minute occurrences, and use the fitted values for the last five years of the sample.[14]
Were FOMC members (and staff) talking about the stock market at the same time that there was a stock market bubble? Figure 1 plots 1,000 times the ratio of keywords to total words in the transcripts (the black line), along with the equity risk premium described in more detail in Section 5 (the grey line).[15] The two series have a correlation of −0.42 (robust s.e. = 0.07).[16] As the stock market became a concern in the mid 1990s, the frequency with which it was mentioned at FOMC meetings rose dramatically. As the equity premium fell in the early 1990s, the frequency of the keywords started to rise, peaking just before the equity risk premium bottomed out. As the stock market boomed, the FOMC members increased the rate at which it was mentioning equities.
5. What Was the FOMC Doing?[17]
Was this cheap talk? Or, did the equity prices place a material role in interest rate decisions? To characterise the actions of the FOMC, I adopt the now standard framework of estimating a policy reaction function, or Taylor rule. In his original work, John Taylor (1993) characterised his now famous policy rule as a description of the Federal Reserve behaviour from the mid 1980s through the early 1990s. That is, he suggested that what the FOMC actually did was to set the nominal federal funds rate target so that

where r is the nominal federal funds rate, πt is current inflation, π is the inflation target (Taylor set this to 2 per cent), and yt is the percentage deviation of actual output from a measure of potential or trend output. Clarida, Galí and Gertler (1998, 2000) have suggested estimating a forward-looking version of this interest-rate rule based on the view that policy-makers are forward-looking. That is, starting with a simple macroeconomic model, they derive a reaction function of the form
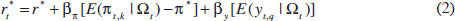
where 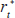 is the desired (equilibrium) short-term interest
rate, r is the equilibrium real interest rate plus the inflation target,
πt,k is inflation from t to t+k,
yt,q is the average output gap from t to t+q,
and
is the desired (equilibrium) short-term interest
rate, r is the equilibrium real interest rate plus the inflation target,
πt,k is inflation from t to t+k,
yt,q is the average output gap from t to t+q,
and 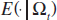 is the expectation conditional on information at
t. In the experiments below, I set target inflation π
equal to a Hodrick-Prescott trend of inflation
in the sample, and the equilibrium real interest rate equal to a constant
2 per
cent.[18]
The observed interest rate adjusts smoothly to this desired level according
to the partial adjustment equation
is the expectation conditional on information at
t. In the experiments below, I set target inflation π
equal to a Hodrick-Prescott trend of inflation
in the sample, and the equilibrium real interest rate equal to a constant
2 per
cent.[18]
The observed interest rate adjusts smoothly to this desired level according
to the partial adjustment equation

where ρ(L) is a polynomial in the lag operator L such that ρ(1)= ρ, and υt is an i.i.d. random variable that we can think of as a monetary policy control error resulting from things like unanticipated shifts in the demand for bank reserves.
Equation (3) summarises the standard view that policy-makers are responding smoothly to a combination of inflation and output gaps. The question is whether they also respond to equity-price bubbles and banking system stress. To see, we can augment Equation (2) with measures of each. That is, I study
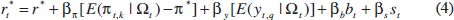
where bt is a measure of the bubble in the stock market and st is a measure of the stress in the banking system. The task is to estimate the reaction of interest rates to each one of these.
I start with estimates of the equity premium constructed from a simple dividend-discount (i.e. Gordon) model.[19] That is, I take the dividend yield from the Standard and Poor's 500 index, and subtract both an estimate of the dividend growth (adjusted for share repurchases) and an estimate of the risk-free interest rate taken from the US Treasury market. The results are plotted in Figure 2 (and are the basis for the grey line in Figure 1).
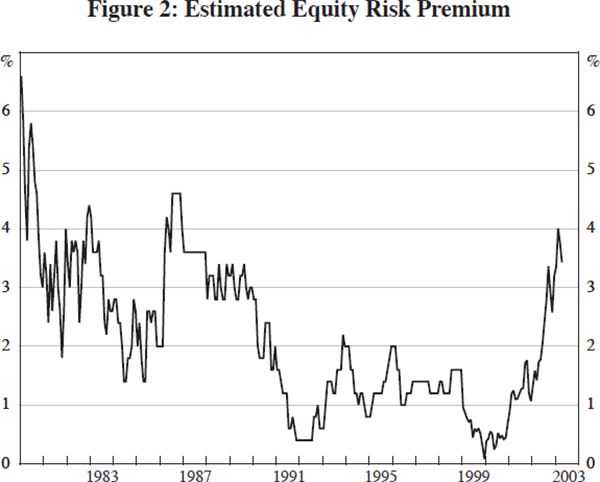
These estimates of the equity premium are the basis for my estimate of the size of the bubble. To allow for the possibility that the equity premium has a low-frequency trend, I estimate misalignments in equity prices as the deviation of the estimated equity premium from a 20-year lagged moving average. Figure 3 shows the path of the excess equity risk premium since 1980. A negative excess equity risk premium suggests that stocks are overvalued and so there is a bubble.
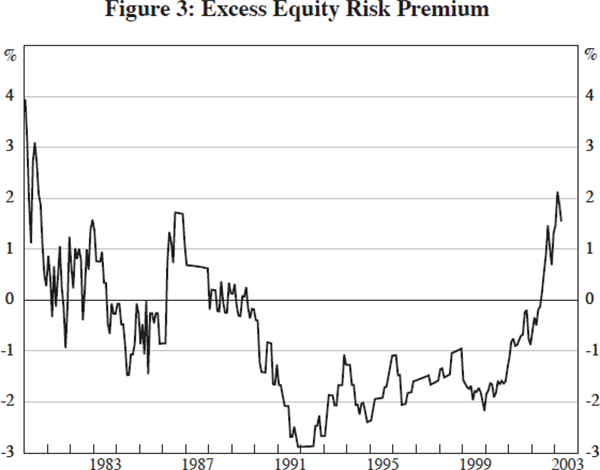
This figure may look surprising at first glance, as the bubble of the late 1990s is not very prominent – certainly not as prominent as it is in the raw equity premium data. The explanation for this is in the mechanics of the way in which the excess equity risk premium is computed. Using a backward-looking moving average means that as the equity premium slowly falls, the excess is small. Looking back at Figure 2, you will notice that the estimates of the equity risk premium fall dramatically at the beginning of the 1990s, and stay at this lower level until the beginning of the current decade. This explains the pattern.
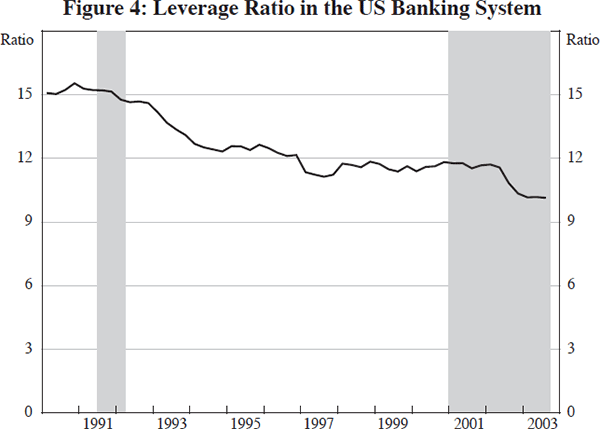
To account for banking system stress, I include a measure of the banking system leverage ratio. That is, the ratio of total assets to total capital, both taken from the call reports. Figure 4 plots these data. There has been a clear downward trend in the data that can be ascribed to changes in prudential regulator standards during the 1980s. In addition, notice the tendency for the leverage ratio to rise slightly during the late 1990s.
To estimate the model, start by substituting the augmented Taylor rule (4) into the partial adjustment formula Equation (2), assuming three lags in ρ (L). The resulting expression is estimated using Generalised Method of Moments (GMM) using quarterly data from 1990 to 2003.[20] The results, together with robust standard errors that take account of the fact that the data are overlapping, are reported in Table 1.
| Policy rule | Inflation gap βΠ | Output gap βy | Equity market bubble | Banking system stress | Sum of adjustment lags ρ | Test of over-identifying restrictions | Goodness of fit (R2) |
|---|---|---|---|---|---|---|---|
| Consumer price index | |||||||
| 0.34 | 0.57 | 0.23 | 0.51 | 0.80 | |||
| (0.30) | (0.00) | (0.00) | |||||
| 0.20 | 0.57 | 0.09 | 0.25 | 0.80 | 0.81 | ||
| (0.24) | (0.00) | (0.47) | (0.00) | ||||
| 0.46 | 0.41 | −0.17 | 0.41 | 0.94 | 0.86 | ||
| (0.03) | (0.00) | (0.02) | (0.00) | ||||
| 0.67 | 0.50 | −0.65 | −0.23 | 0.40 | 0.88 | 0.88 | |
| (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | |||
| PCE chain-type price index | |||||||
| −0.42 | 0.70 | 0.29 | 0.61 | 0.84 | |||
| (0.29) | (0.00) | (0.00) | |||||
| −0.18 | 0.68 | 0.06 | 0.30 | 0.87 | 0.85 | ||
| (0.51) | (0.00) | (0.64) | (0.00) | ||||
| −0.20 | 0.62 | −0.12 | 0.40 | 0.96 | 0.87 | ||
| (0.21) | (0.00) | (0.00) | (0.00) | ||||
| 0.27 | 0.63 | −0.53 | −0.16 | 0.40 | 0.91 | 0.88 | |
| (0.30) | (0.00) | (0.00) | (0.00) | (0.00) | |||
| Notes: GMM estimates of Equation (4) substituted into Equation (2). Numbers in parentheses are p-values for the test that the coefficient estimate is equal to zero. When p-values are 5 per cent or lower, the coefficient is printed in bold face. Sourced from data appendix in Cechetti and Li (2003). | |||||||
A full set of results is presented for two measures of inflation: the consumer price index and the chain-type price index for personal consumption expenditure.[21] The two sets of results give the same overall picture, and so I will focus my discussion on the top panel, the one reporting results using the conventional CPI. The first row reports results for a traditional Taylor rule. The rule-of-thumb is that for the model to be well-behaved, the coefficient on inflation has to be positive (recall Taylor's original rule-of-thumb was to set βπ equal to one-half). Using the CPI, the coefficient on the inflation gap is one-third, although it is imprecise, while the estimate of the coefficient on the output gap is very nearly one-half.
Turning to the final line of each panel, we see that the data support adding measures of an equity bubble and banking system stress to the policy rule. Remember that a bubble is measured as a negative excess equity risk premium. If policy-makers increased interest rates in the face of a bubble, this would show up as a negative coefficient in the reaction function. That's exactly what's in Table 1. A 1 percentage point reduction in the equity premium leads to a two-thirds of a percentage point increase in the interest rate, all other things equal.
While it is possible that the excess equity premium measure is showing up because of its correlation to something else that is omitted from the policy reaction function, it is difficult to see what that might be. It is, however, likely that the FOMC is not reacting directly to the bubble. The most plausible explanation for these findings is that policy-makers are reacting to the extent that assumed asset-price fluctuations create variation in forecasts of consumption, through their impact on wealth, and investment, due to changes in the ease with which firms can obtain financing.
The reaction to financial system stress is also as we would expect. An increase in the leverage ratio is a sign that bank balance sheets are coming under pressure. All other things equal, this is met with a decline in the interest rate. The estimates suggest that a 1 percentage point increase in banking system leverage leads to a 25 basis point cut in the federal funds rate. Taken together, we can adjust Taylor's original rule-of-thumb to include the excess equity risk premium (bt) and the banking system leverage ratio (st):

This is very similar to the rule-of-thumb studied in Chapter 4 of Cecchetti et al (2000). While we were proposing it, they were doing it – and had been for years!
To understand the consequences of this change, we can look at the pattern of interest rates over the 1990 to 2003 period. Figures 5 and 6 plot the effective federal funds rate against the fitted values from the simple forward-looking Taylor rule (the first line in Table 1) and the augmented Taylor rule (the fourth line of Table 1). The differences in the two figures are subtle. The augmented model does better in the first half of the sample by taking account of financial system stress, and in the latter half by including the excess equity premium.
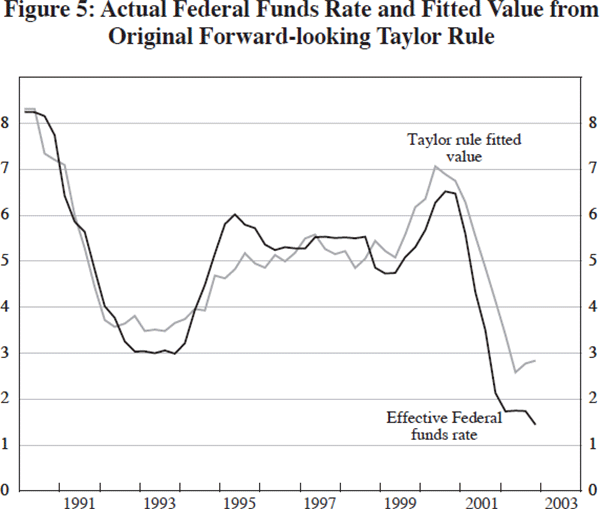
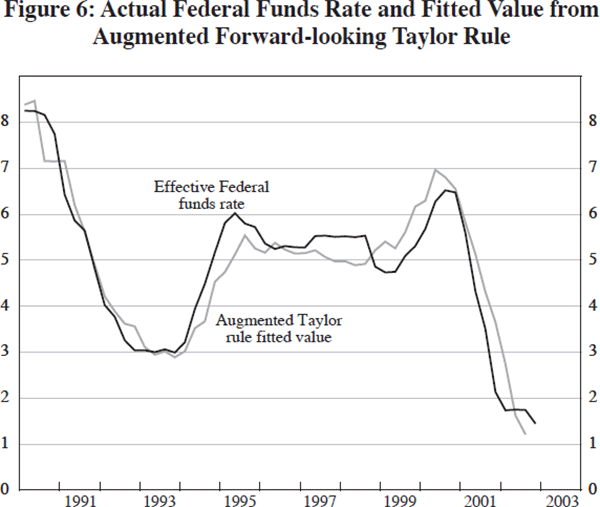
These results are not robust to replacing the excess equity risk premium with the equity risk premium itself. The analog to the fourth line in Table 1, the model based on the CPI, results in a coefficient estimate on the equity risk premium of −0.10 with a standard error of 0.15. That is, an estimated effect that is both smaller in absolute value and much less precise. Taken together with the results in Table 1, this suggests that the FOMC is in fact reacting to something like a bubble.
Cecchetti and Li (2003) report results similar to those in Table 1 from both Germany and Japan. These are reproduced in Table 2. The German augmented Taylor rule, estimated over the period from 1979 to 1993, suggests that the Bundesbank set interest rates taking account of the domestic German stock market and leverage in the banking system. While Japan appears to have reacted aggressively to the equity market bubble, the response to changes in the banking system leverage ratio has the wrong sign. All other things equal, increased leverage in the Japanese banking system was associated with an increase in interest rates.
| Inflation gap | Output gap | Equity market bubble | Banking system stress | Sum of adjustment lags ρ |
Goodness of fit (R2) | ||
|---|---|---|---|---|---|---|---|
| US | 0.67 | 0.50 | −0.65 | −0.23 | 0.40 | 0.88 | |
| 1990–2003 | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | ||
| Germany | 1.23 | 0.31 | −0.39 | −0.58 | 0.95 | 0.98 | |
| 1979–1993 | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | ||
| Japan | 1.99 | 0.36 | −1.46 | 0.11 | 0.97 | 0.99 | |
| 1979–2001 | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | ||
|
Notes: GMM estimates of Equation (4) substituted into Equation (2). Numbers in parentheses are p-values for the test that the coefficient estimate is equal to zero. When p-values are 5 per cent or lower, the coefficient is printed in bold face. Source: Cecchetti and Li (2003) |
|||||||
6. Conclusion
In August 2002, citing evidence that stock prices rose following the series of federal funds rate increases ending in February 1989, February 1999 and May 2000, Chairman Alan Greenspan concluded:
It seems reasonable to generalize from our recent experience that no low-risk, low-cost, incremental monetary tightening exists that can reliably deflate bubble. But is there some policy that can at least limit the size of the bubble and, hence, its destructive fallout? From the evidence to date, the answer appears to be no. (Greenspan 2002, p 5)
The immediate reaction to this was very harsh. How, given the problems in the intervening years, could he defend the FOMC's failure to respond to the Internet bubble as it was happening? In light of the evidence presented here there is a second interpretation that might be more apt. That is, the Chairman is saying that they tried and failed. Doing any more, in his view, would have been catastrophic.
The case for this more flattering view starts with the observation that during the period of the bubble, the Board staff forecasts used by the FOMC were based on an assumed decline in the stock market. And the Board staff works for the Chairman, so he clearly knew about this. Add to this the fact that FOMC members increased the intensity with which they discussed the stock market as it rose, and the evidence that the federal funds rate reacts to measures of asset-price misalignments, and we come to the conclusion that policy-makers were doing what they could. Aware of the possibility that equity prices very well might collapse, and understanding the disruptive consequences of a stock market bust, the FOMC took out small amounts of bubble insurance. Greenspan argues that it would have been risky to do more. Is he right? That is where the debate should shift now.
Footnotes
Professor of International Economics and Finance, International Business School, Brandeis University; and Research Associate, NBER. This paper was prepared for the Reserve Bank of Australia's annual research conference on Asset Prices and Monetary Policy in Sydney, 18–19 August 2003. I would like to thank Lianfa Li and Craig Evers for excellent research assistance, as well as Blake LeBaron and Jeremy Stein for discussions that help clarify some of my fuzzy thinking, and the conference participants for their comments. Finally, I continue to owe a substantial debt to both Hans Genberg and Sushil Wadhwani with whom I started the research program of which this is the next instalment. I am responsible for all the remaining errors, ambiguities, and policy prescriptions. [1]
These assumptions were called ‘Mike's assumptions’ as they were ascribed to Michael Prell, the Director of the Division of Research and Statistics and the person responsible for the preparation of the Green Book at the time. [2]
In fact, in an essay written immediately prior to my time in the Federal Reserve, I wrote that one of the Great Depression's lessons for current policy is that ‘if central bankers allow fluctuations in asset market prices to affect their decisions, it may distract them from concentrating on some combination of output growth and inflation. The focus of the Federal Reserve on the level of equity prices in 1929 clearly led to a disastrously contractionary path for policy’ (Cecchetti 1998, p 178). This is no longer my view. [3]
The pension fund story is particularly worrisome. The bulk of American pension funds are privately managed. Rules allow for companies to withdraw funds from their pension systems when their actuaries find them to be overfunded based on their interpretation of the accounting rules. Companies have an incentive to make these withdrawals, as they add to reported profits, so many did it. In retrospect this was not very prudent. By some estimates, the pension funds are now short in excess of US$300 billion. [4]
See the excellent essays in Chapter II of IMF (2003) for a summary of the evidence. [5]
See Cecchetti et al (2000) and Cecchetti, Genberg and Wadhwani (2003). [6]
The debate over whether interest rate policy should respond to asset-price misalignments is distinct from the question of whether asset prices should be included in measures of inflation. That is, whether asset prices should enter central bank objectives through the back door of their inclusion in the targeted price index. Bryan, Cecchetti and O'Sullivan (2001, 2002) take up this question in detail and conclude that the answer is yes for housing, but no for equity. [7]
Entrepreneurial net worth is the critical factor in determining creditworthiness in a world with asymmetric information. The primary way to reduce both adverse selection and moral hazard is to insist that the owners of firms seeking financing have a sufficient stake in their own success. This is the mechanism that is at the foundation of the lending view of monetary policy transmission first described by Bernanke and Gertler (1989). [8]
Stein's model is a version of the Shleifer and Vishny's (1997) ‘limits to arbitrage’. [9]
Even if a manager has the fortitude to take the short position, it can be difficult to maintain. Since the market is moving against the position, the manager will have to constantly post additional margin to maintain it. And since the lender of the stock can always recall share without notice, there is always the possibility of being closed out before the bubble bursts. For a thorough discussion of the institutional details of short selling see d'Avolio (2002). [10]
In his paper for this volume, Charles Bean discusses this issue in some detail. His conclusion is that the solution is for central bankers to change their rhetoric, moving toward statements that clearly imply longer time horizons and less stringent adherence to short-term inflation targets. [11]
As Frank, the alien disguised as a dog in Men in Black said when referring to a galaxy that was being hidden in a charm on a cat's collar: ‘You humans, when're you gonna learn that size doesn't matter? Just ‘cause something's important, doesn't mean it's not very, very small’. [12]
A large set of the documents is available in searchable PDF format, so the work was done completely mechanically. For the earlier transcripts, where the Federal Reserve has posted scanned bitmaps, someone with no experience in reading FOMC documents read the documents. [13]
For a detailed description of what goes on at an FOMC meeting see Meyer (1998). [14]
The aperiodic frequency of FOMC meetings means the grey line in Figure 1 is not directly comparable to the line in Figure 2. [15]
The correlation of the keyword frequency with the excess equity risk premium that is the focus of the next section is −0.23 (robust s.e. = 0.06). [16]
This section is based on work reported in detail in Cecchetti and Li (2003). [17]
This assumption is almost surely not innocuous, but it is hard to know what to do about it. The fact is that the equilibrium or neutral real interest rate surely changes over time as the growth rate of the economy changes. See Warwick McKibbin's comment following this paper for a discussion of the likely importance of this issue. [18]
That is, the equity premium is estimated as the dividend yield minus the risk-free interest rates, plus the growth rate of dividends of 2.35 per cent, adjusted for stock repurchases of 0.9 per cent. From 1998 on, the real risk-free rate is the interest rate on Treasury index bonds. Prior to that, it is estimated from the Treasury bonds minus realised inflation. [19]
The information set in the estimation used three lags of the federal funds rate, the inflation index in the policy rule, the output gap, producer price inflation, growth in M2, the spread between the 10-year Treasury bond yield and the yield on 3-month Treasury bills, the excess equity risk premium, and the leverage ratio. [20]
As students of American monetary policy know, the FOMC, and Chairman Greenspan in particular, follow the PCE chain-type index closely. As a chained index, the PCE does not suffer some of the well-known biases that plague fixed-weight price indices like the CPI. [21]
References
Bernanke BS (2002), ‘Asset-price “bubbles” and monetary policy’, remarks before the New York Chapter of the National Association of Business Economics, New York, 15 October. Available at <http://www.federalreserve.gov/boarddocs/speeches/2002/20021015/default.htm>.
Bernanke BS and M Gertler (1989), ‘Agency costs, net worth, and business fluctuations’, American Economic Review, 79(1), pp 14–31.
Bernanke BS and M Gertler (2000), ‘Monetary policy and asset price volatility’, in New challenges for monetary policy: a symposium sponsored by the Federal Reserve Bank of Kansas City, Federal Reserve Bank of Kansas City, Kansas City, pp 77–128.
Bernanke BS and M Gertler (2001), ‘Should central banks respond to movements in asset prices?’, American Economic Review, 91(2), pp 253–257.
Borio C, C Furfine and P Lowe (2001), ‘Procyclicality of the financial system and financial stability: issues and policy options’, in Marrying the macro- and micro-prudential dimensions of financial stability, BIS Papers No 1, Basel, Switzerland, pp 1–57.
Borio C and P Lowe (2002), ‘Asset prices, financial and monetary stability: exploring the nexus’, BIS Working Paper No 114.
Bryan MF, SG Cecchetti and R O'Sullivan (2001), ‘Asset prices in the measurement of inflation’, De Economist, 149(4), pp 405–431.
Bryan MF, SG Cecchetti and R O'Sullivan (2002), ‘A stochastic cost-of-life index’, in WC Hunter, GG Kaufman and M Pomerleano (eds), Asset price bubbles: the implications for monetary, regulatory, and international policies', MIT Press, Cambridge, Mass, pp 277–290.
Cecchetti SG (1998), ‘Understanding the great depression: lessons for current policy’, in M Wheeler (ed), The economics of the Great Depression, WE Upjohn Institution for Employment Research, Michigan, pp 171–194.
Cecchetti SG, H Genberg, J Lipsky and S Wadhwani (2000), Asset prices and central bank policy, Geneva Reports on the World Economy No 2, International Center for Monetary and Banking Studies and Centre for Economic Policy Research, Geneva.
Cecchetti SG, H Genberg and S Wadhwani (2003), ‘Asset prices in a flexible inflation targeting framework’, in WC Hunter, GG Kaufman and M Pomerleano (eds), Asset price bubbles: the implications for monetary, regulatory, and international policies', MIT Press, Cambridge, Mass, pp 427–444.
Cecchetti SG and L Li (2003), ‘Do capital adequacy requirements matter for monetary policy?’, Ohio State University, unpublished manuscript.
Clarida R, J Galí and M Gertler (1998), ‘Monetary policy rules in practice: some international evidence’, European Economic Review, 42(6), pp 1033–1067.
Clarida R, J Galí and M Gertler (2000), ‘Monetary policy rules and macroeconomic stability: evidence and some theory’, Quarterly Journal of Economics, 115(1), pp 147–180.
d'Avolio G (2002), ‘The market for borrowing stock’, Journal of Financial Economics, 66(2/3), pp 271–306.
Dupor B (2002), ‘Nominal price versus asset price stabilization’, The Wharton School, University of Pennsylvania, unpublished manuscript.
Gilchrist S and JV Leahy (2002), ‘Monetary policy and asset prices’, Journal of Monetary Economics, 49(1), pp 75–97.
Greenspan A (2002), ‘Economic volatility’, remarks at a symposium sponsored by the Federal Reserve Bank of Kansas City, Jackson Hole, 28–30 August.
Hardouvelis GA (2003), ‘Asset prices and the need for new policy instruments: the case of countercyclical margin policy’, paper presented for the International Symposium of the Banque de France, Paris, 7 March.
Hardouvelis GA and P Theodossiou (2002), ‘The asymmetric relations between initial margin requirements and stock market volatility across bull and bear markets’, Review of Financial Studies, 15(5), pp 1525–1559.
IMF (International Monetary Fund) (2003), World economic outlook, Washington DC.
Meyer LH (1998), ‘Come with me to the FOMC’, remarks at The Gillis Lecture, Willamette College, Oregon, 2 April.
Mishkin FS and EN White (2002), ‘U.S. stock market crashes and their aftermath: implications for monetary policy’, NBER Working Paper No 8992.
Schwartz AJ (2002), ‘Asset price inflation and monetary policy’, NBER Working Paper No 9321.
Shleifer A and RW Vishny (1997), ‘The limits to arbitrage’, Journal of Finance, 52(1), pp 35–55.
Stein JC (2003), ‘Why are most funds open-end? Competition and the limits to arbitrage’, Harvard University, unpublished manuscript.
Taylor J (1993), ‘Discretion versus policy rules in practice’, Carnegie-Rochester Conference Series on Public Policy, 39, pp 195–214.