RBA Annual Conference – 1997 Which Monetary-policy Regime for Australia? Warwick McKibbin^[*]

1. An Assessment

There is a vast literature on the choice of monetary regimes that spans both theoretical and empirical insights. In this paper I draw on some of this literature as well as a recent research project at the Brookings Institution in which I was involved with Dale Henderson from the Federal Reserve in Washington.^[1] This project was intended to cover a wide theoretical and empirical literature on monetary-policy regimes and draw out implications for actual policy implementation. The outcome of some of that research was published in the Brookings volume on ‘Evaluating Policy Regimes: New Research in Empirical Macroeconomics’ (eds Bryant, Hooper and Mann 1993). What did we learn from that research that can guide the choice of a monetary-policy regime for Australia?

A casual observer (with an engineering bent) might ask why the Reserve Bank has not worked it out yet? If you have the right model of the Australian economy (such as the McKibbin and Sachs Global model, for example), why not write down the objectives of the policy-maker and maximise this objective function (or minimise the loss function depending on the personality of the policy-maker) subject to the constraints imposed by the structure of the economy. We have learnt in the past few decades that you may want to impose other constraints such as the desire to write the optimal policy as a closed-loop rule to make it more operational (i.e. a rule in which the instrument of policy is a function of all state and exogenous variables in the economy). You could even impose on the optimisation that the rule selected be restricted to the set of time-consistent policy rules to incorporate the insight of Kydland and Prescott (1977) and Barro and Gordon (1983). Indeed, this has been done using simple as well as complex econometrically estimated models (McKibbin and Sachs 1988, 1989, 1991). You could argue that this approach underlay the ‘check-list’ approach to monetary policy that was popular in the Reserve Bank in the 1980s (Jonson and Rankin 1986; Stemp and Turnovsky 1989). The outcome of such a constrained optimisation would be a complex feedback rule in which the policy instrument responds to a range of information (both domestic and foreign) available in a given period.

In practice, the presence of uncertainty about the ‘true model’ complicates the above derivation of the optimal feedback rule. Nonetheless, calculating optimal rules gives a benchmark against which to evaluate other rules. As well, the issue of credibility can be very important when there is great uncertainty about which is the true model. If the Reserve Bank actually calculated the optimal rule (presumably trading off inflation and unemployment objectives), how do agents really know the Reserve Bank is not cheating on the rule when it is so complex as to be indistinguishable from complete discretion? One way to get around this problem is to simplify the rule so that the amount of information needed to monitor adherence to the rule is minimised and therefore trade off the gains from credibility against the loss from deviating from the fully optimal rule. In this case you could constrain the set of information in the feedback rule to a reduced set of variables which are observable or can be inferred in any given period. Thus you could compress the entire problem into an optimal but simple feedback rule for policy.^[2] Simple rules for policy are very popular these days although the issue of optimal simple rules is dealt with less often.

A serious problem with any policy rule is its robustness. It is desirable that a policy rule not only perform well in the model that it was developed in but also does not perform disastrously in an alternative model of the economy. The robustness aspect of regime choice was one of the underlying themes of the Brookings research. Is there a robust policy rule that performs well across a range of alternative empirical representations of the economy?

Given that the current weight of opinion is on the desirability of simple rules either because of issues of credibility or because of doubts about what discretionary policy can achieve or doubts about the transmission mechanism (Grenville 1995), what issues emerge in the choice of a simple feedback rule? The first issue is what should be the instrument of monetary policy. The second is what variables should appear in the rule. The third issue is the size of the feedback coefficients or how quickly policy should respond to the deviation of intermediate targets from their desired values.

On the policy instrument, most economists agree that the current institutional arrangements for implementing monetary policy make a short-term interest rate the appropriate monetary instrument (Edey 1989, 1997). Issues of price-level indeterminancy with an interest-rate instrument are a real concern, but as shown in Gagnon and Henderson (1990) and Henderson and McKibbin (1993a), as long as there is some nominal anchor in the objective of policy, using the interest rate as the policy instrument is not such a problem.

The second issue is what should be the intermediate target or the variable(s) within the rule to which interest rates respond over some time period. This is where the debate becomes less clear. Going back through the literature on regime choice there is a variety of candidates. Indeed, the early literature of regime choice for monetary policy that underlies most current analytical evaluations can be traced back to the classic article by Poole (1970). Poole used a simple closed-economy theoretical model and compared the performance of a rule of a fixed stock of money with a fixed interest-rate rule, under shocks to money demand and goods demand. A number of papers have extended this form of analysis to open economies (Roper and Turnovsky 1980) and a wide range of shocks including oil price shocks and supply shocks (Henderson and McKibbin 1993b). The set of possible regimes has also expanded from the fixed interest-rate and fixed money regime to regimes that target nominal income (Corden 1981; Meade 1978; Tobin 1980) and other forms of rules, such as rules with feedback on inflation and output gaps according to the Bryant, Hooper, and Mann (BHM) (1993) rules.

How should the variables that appear in the feedback rule be chosen? A crucial result from the Brookings project is that within the class of simple rules, the choice of the ‘best rule’ is an empirical question. In Henderson and McKibbin (1993a), we show that the choice depends on the nature of the shocks that hit the economy, the structure of the economy (in particular the degree of price stickiness which, in our case, was the degree of wage persistence) and the size of the feedback coefficient or what we referred to as the degree of instrument adjustment. In addition, the ultimate policy targets used to evaluate the regimes are important since we show that the ranking of regimes in terms of inflation variability differs from rankings for unemployment, which differs from rankings for output in the case of productivity shocks. The model simulations that were designed in the Brookings volume were then used to put some empirical flesh on the theoretical bones to see if a wide range of models could be used to pick out relatively robust policy rules.

In Henderson and McKibbin (1993a, b) we considered temporary shocks to money demand, goods demand and productivity under rules with varying degrees of instrument adjustment (under alternative degrees of wage persistence) to target: interest rates; a measure of the money stock; nominal income; and an unweighted sum of inflation and output deviation from potential. This last regime, which we called the CC regime with equal and unit weights on inflation and output gap (where the weights came from experiments with the MSG2 model), is currently known as the Henderson-McKibbin Rule in the Fed. A similar rule with a weight of 0.5 on output and inflation separately relative to desired is currently called the Taylor Rule in popular discussions. Both rules should really be called the BHM rule but actually significantly predate that identification. To be consistent with the notation in Henderson and McKibbin (1993a, b), I will refer to this regime as the CC regime where the results are weight-specific from our paper or I will refer to this class of rules generically as the BHM rule. The exact form of these rules is shown in Table 1.

Table 1: Alternative Rules

Money Rule:
Nominal-income Rule:
Bryant-Hooper-Mann Rules:
Henderson-McKibbin (or CC) Rule:
Taylor Rule:
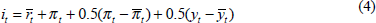where: i = nominal interest rate; r = real interest rate; π = inflation rate; ρ = log of price level; y = log of output; m = log of money; and a bar over a variable indicates a desired value.

It was clear from the theoretical results that we explored (before turning to the large-model simulations) that in the case of shocks to money demand, a fixed money rule was dominated by other regimes. For other shocks the results are ambiguous but a fixed money rule or a fixed interest-rate rule was usually dominated by the nominal-income and CC rules.

In the case where there is no wage persistence, the nominal-income and CC rules are equivalent and dominate the other regimes. For a global demand shock the nominal-income rule minimises employment and output deviations for low feedback coefficients but the CC rule minimises inflation deviations across all feedback coefficients. This contrasts with a country-specific demand shock in which the nominal-income regime dominates on inflation as well. For both global and country-specific productivity shocks the nominal-income rule works well for employment but is dominated by the CC regime for output and inflation.

Once wage persistence is introduced into the analysis, the results become less clear for the relative performance of the nominal-income rule and the CC rule. The equivalence of these rules breaks down. A clear result that emerges is that the CC rule handles the impact of a temporary global productivity shock on employment much better than the nominal-income rule in the MSG2 model over the full range of feedback coefficients. The reason for this is clear from the model specification. For a fall in productivity, as output falls and prices rise there is less adjustment under the nominal-income rule because nominal income is little changed. In contrast, under the CC regime as output falls interest rates fall which offsets the loss in employment. The rise in inflation is slow to emerge because of wage persistence. When inflation does begin to emerge, the recovery in output occurs while inflation is rising which causes interest rates to rise and dampen the inflationary impulse. In this particular case, the CC regime clearly dominates the nominal-income target because of the nature of the particular dynamic structure of the MSG2 model. This does not show up in the simpler theoretical models.

A final issue that emerged from the exploration of simple optimal rules versus fully optimal rules in McKibbin (1993) that is worth repeating, is that some simple rules such as the CC rule can dominate the fully optimal rule under some circumstances. In that paper the shocks were drawn from an estimated world variance-covariance matrix of shocks. In this case, the CC regime led to lower variance for a range of target variables than the fully optimal complex time-consistent policy rule. This result is possible when one considers that in that paper the optimal rule was chosen from the set of time-consistent policy rules. However, the simple rules evaluated in the Brookings project are not part of the optimal set of policy rules available under the condition of time consistency. The sustainability of these simple rules therefore depends crucially on the exogenously specified credible commitment of the central bank to the simple rule. This other aspect of credibility should be kept in mind, i.e. the simple rules are not necessarily time consistent unless there is some form of external credible commitment.

2. Conclusion

What did we learn from the Brookings research of relevance to the Australian debate on monetary regimes? The first lesson is that money targeting is dominated by other regimes. Both the nominal-income target and the inflation plus output deviation from potential targets (what I call the BHM rule) dominate the other money and interest-rate targeting rules. The attractiveness of the preferred policy rules, whether in the form of the BHM rule (or various forms of this rule called the Taylor Rule or the Henderson-McKibbin Rule), is dependent on the type of shocks hitting the economy. Where productivity shocks or supply-side shocks are dominant, the nominal-income rule has a number of drawbacks relative to the BHM rule. First, if real output returns to trend there is a tendency for policy to have to drag the price level back to baseline which can have additional output losses along a transition path. This has already been widely discussed in the literature on price-level drift or base drift in the early money-stock targeting debates (Hansen 1996). It is unlikely for most objective functions that the gains to returning the price level to the desired level can justify the loss in real output during the transition. The second advantage of the BHM class of rules over nominal-income targeting is that when there is significant wage persistence, the fall in output may induce a lowering of interest rates to offset the employment loss before prices begin to rise. As output recovers and prices rise, interest rates rise appropriately thus giving a better employment and output performance than a nominal-income rule. This result depends crucially on the nature of the wage dynamics in the economy as well as the size of the weight on inflation in the output inflation feedback rule (0.5 appears optimal in Taylor-type models, whereas unity is better in MSG2 type models). Nonetheless, these theoretical results and results from the MSG2 model suggest that indeed there is such a gain from this type of rule relative to the pure nominal-income rule.

What does all this mean for the evaluation of current Reserve Bank policy? It would appear that the current policy of ‘targeting inflation over the cycle’ is close to a rule from the class of BHM rules that in many cases in the Brookings project were found to dominate the alternative simple rules. What the exact weights are on this rule currently in Australia is unclear (probably just as much to Reserve Bank officials as to outside observers). A case could be made that to maximise the credibility gain from moving to a simple rule, as the Bank has clearly done since the early 1990s, it would be helpful for the Reserve Bank to be more specific on what the parameters are. In addition, a case can be made that there should be less uncertainty surrounding the timing of changes in interest rates in response to changes in these variables (or at least in response to changes in the expected outcomes of the targets depending on the way the rule is actually implemented). In the words of the above summarised literature, there should be a more explicit statement of the size of the feedback coefficient or the degree of instrument adjustment.

A final issue that should be considered is the extent to which a simple policy rule will be, or should be, sustained if and when the next big shock hits the Australian economy. Whether it is optimal to stick to a simple rule under all circumstances is open to debate. We know that time-consistent discretionary policy may dominate simple rules, but credibility arguments rule out discretion in most moderate circumstances. However, in the face of a large shock, it is possible that sticking to a simple rule at all costs will probably be suboptimal and most likely will not be credible anyway (given that exogenous commitment is all that holds the rule in place). Thus, rather than sit back and feel comfortable about where the monetary-policy regime has settled in Australia, it is crucial to continue to improve our understanding of the Australian economy and its place in the global economy, through continued investment in theoretical and empirical research. When the time comes to deviate from the simple monetary-policy rule onto which we have currently converged in relatively calm times, the deviation in monetary policy will need to be done appropriately and swiftly. The more we understand about the economy, the more likely the policy adjustment will work in the right direction to lower the costs of large economic shocks rather than exacerbate these costs, as unfortunately has been the case in many previous episodes of significant monetary-policy adjustment in Australia.