RBA Annual Conference – 1997 Discussion
1. Tiff Macklem[*]
Once the objective of monetary policy has been established, the next question is how best to achieve this objective. With central banks increasingly focusing on the objective of maintaining low and stable rates of inflation, research on the question of how best to accomplish this objective has expanded rapidly, both in academia and at central banks. The paper by Gordon de Brouwer and James O'Regan provides a valuable addition to this literature, and will no doubt serve as a benchmark for future research on monetary-policy rules for the Australian economy. Their analysis of alternative policy rules proceeds in two steps.
In the first step, they examine the stochastic behaviour of the Australian economy under several familiar types of monetary-policy rules, including a nominal-income rule, an inflation-only rule, a Taylor rule and a price-level rule. All the rules are constrained to be backward-looking, by which I mean they do not include any expected future values of the variables in the rule. The conclusion that emerges from this analysis is that the Taylor rule is the best rule in the sense that it yields both lower inflation variability and lower output variability. As the authors point out, this arises because future inflation is determined largely by the current output gap, so by responding to the current excess demand, the monetary authority also reduces the variability of inflation.
In the second step, de Brouwer and O'Regan go on to consider three important issues for monetary control: the implications of increased credibility for low stable inflation; the role for an explicit open-economy dimension in the monetary rule; and the potential for forward-looking rules to outperform backward-looking rules. Perhaps because they find the Taylor rule is ‘best’ in the first-stage analysis, de Brouwer and O'Regan examine each of these three issues in the context of the Taylor rule alone. The main conclusions can be summarised as follows:
- Credibility is a good thing in the sense that it shifts the efficient policy frontier for the Taylor rule closer to the origin, allowing lower output and inflation variability to be simultaneously achieved.
- In an open economy such as Australia's, adding the deviation of the real exchange rate from its equilibrium value to a Taylor rule can, for some parameter values, reduce both the variability of output and inflation.
- Forward-looking ‘Taylor’ rules tend to outperform the standard version which uses contemporaneous values of the output gap and the deviation of inflation from target.[1]
I have summarised de Brouwer and O'Regan's main findings because, as far as they go, I think they are exactly right. In addition, the authors do a good job of explaining why these results come about. I particularly appreciate the care that was taken to discuss what features of the model explain why some of the finer points of the results differ from those in previous work on Taylor and nominal-income rules.
So in the rest of my remarks, I want to talk about something that de Brouwer and O'Regan do not do in their paper. What they do not do is reconsider the full set of rules when they examine the implications of increased monetary credibility, the open-economy dimension, and the relative performance of forward-looking rules. I am going to argue that when the implications of these considerations are taken into account for the full set of alternative rules considered in the first step of their analysis, the Taylor rule is unlikely to emerge as the best rule. More specifically, I am going to focus on the two rules that do the worst among the stable rules that de Brouwer and O'Regan consider – the inflation-only rule and the price-level rule – and argue that once these rules are made forward-looking and some attempt is made to address the implications of the Lucas critique, these rules will outperform the Taylor rule.
Forward-looking inflation-only rules
Svensson (1997) and Ball (1997) have recently shown that in the context of a small, linear, closed-economy model, a Taylor rule (using contemporaneous values) is equivalent to a forward-looking inflation-only rule when the lead on inflation is set equal to the control lag in the model between the monetary instrument and inflation. This result reflects the fact that in these simple models, the current output gap and the current rate of inflation are optimal predictors of future inflation. So in a simplified setting, Taylor rules are neither better nor worse than forward-looking inflation rules – they are the same.
This result provides a useful benchmark, but it does not carry over to more realistic settings in which there are other influences on inflation (such as exchange-rate pass-through) or non-linearities in the model (such as an asymmetry in price adjustment). In this setting, which rule is better is again a meaningful question. My hypothesis is that in this setting a forward-looking inflation-only rule will usually outperform a Taylor rule. The intuition for this is as follows. To control future inflation, the monetary authority must lean against the output gap, so the forward-looking inflation rule will stabilise output. The advantage of the forward-looking inflation rule is that the forecast of inflation in the rule is based on the model-consistent solution for inflation, whereas the Taylor rule uses only contemporaneous information on inflation and output to forecast future inflation. The model-consistent solution takes account of the full structure of the model, as well as other useful information for inflation, such as exchange-rate movements. The forward-looking rule therefore uses more information, and this will tend to produce better outcomes.
I do not have an elegant analytic proof of this hypothesis, but I can illustrate it numerically based on a recent paper I co-authored with Richard Black and David Rose (Black, Macklem and Rose 1997; hereafter BMR). In that paper we used a model of the Canadian economy to evaluate alternative policy rules for price stability. The model itself is somewhat different from the model used by de Brouwer and O'Regan, although it embodies the same basic view of the monetary-transmission mechanism. Our model is bigger (about 30 equations describe the essential agent behaviour), it is calibrated rather than estimated, and it has an asymmetry in price adjustment whereby excess demand is more inflationary than an equivalent amount of excess supply is disinflationary. In addition, private agents form forward-looking though not entirely model-consistent expectations, there is complete stock-flow accounting, separate equations for the main components of demand, and reaction functions for both the monetary and fiscal authorities.
As in de Brouwer and O'Regan, the monetary instrument is the short-term interest rate, but we express the reaction function in terms of the spread between short and long rates. The basic inflation-only reaction function is of the form
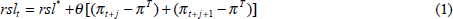
where rsl is the yield spread (the 90-day interest rate less the 10-year rate), rsl* is the equilibrium yield spread, πj is inflation in period j, and πT is the inflation target. We use a two-period moving average of the deviation of inflation from target in the rule to avoid any excess sensitivity to inflation developments in a particular quarter.
Figure 1 shows the efficient policy frontiers in our model generated by two backward-looking versions of the reaction function given in Equation (1). Specifically, the cases shown are j = −1 (so πt−1 and πt are in the reaction function) and j = −2 (so πt−2 and πt−1 are used). As expected, increasing j shifts the frontier towards the origin. These two frontiers should be compared to the frontier for the inflation-only rule that de Brouwer and O'Regan consider.
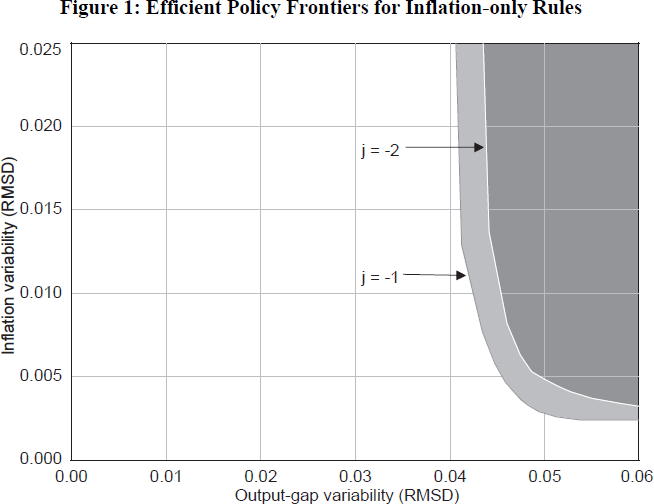
Figure 2 shows the efficient frontier for the reaction function (Equation 1) when j is allowed to vary between −2 and 10. When j > 0, the reaction function uses the expected future rate of inflation j periods ahead, which is defined as the fully model-consistent solution for inflation.[2] As shown, the forward-looking rules (shaded in light grey) do considerably better than the backward-looking versions. Two points on the efficient policy frontier are of particular interest. At point B, j = 4. This is roughly the control lag in the model between movements in the monetary instrument and the direct effects on prices of the associated exchange-rate changes. At point B, inflation control is very good, but output variability remains high. At point A, j = 8, which is roughly the control lag from the monetary instrument to inflation through the output gap. Since the lags in this transmission mechanism are about two years, inflation control is somewhat imprecise, but since it is achieved by dampening cycles in output, output variability is relatively low.
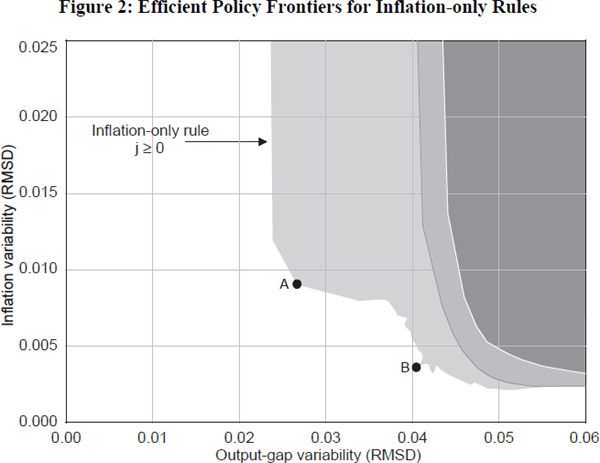
Figure 3 superimposes Figure 2 on the efficient frontier obtained in our model using the Taylor-style rule
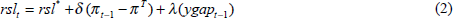
where ygap is the output gap. Following de Brouwer and O'Regan, information is dated at time t−1. The forward-looking inflation-only rule does noticeably better than this Taylor rule. As shown in BMR, if contemporaneous information is used in the Taylor-style rule instead of lagged information, the efficient policy frontiers for the Taylor-style and inflation-only rules are very close in inflation-output variability space, with no clear winner. However, the forward-looking inflation-only rules have the clear advantage along another dimension – they achieve about the same outcomes in output-inflation variability space with considerably less variability in interest rates. The reason is that the inflation forecast that is embodied in the output gap in the Taylor rule is not as good as the model-consistent forecast, so the Taylor-style reaction function includes some extra noise that results in excessive interest-rate volatility.
De Brouwer and O'Regan do implicitly examine forward-looking inflation-only rules since they consider forward-looking Taylor rules and there is nothing preventing the optimal weight on the output gap from falling to zero. Indeed, as they point out, the weight on the output gap does fall when they use leads in the Taylor rule. Their results differ from ours, though, in that they find that the optimal lead is quite short, only about two quarters. This result, however, may be a reflection of the way in which their forward-looking rules are implemented. The j-period ahead variables are determined by the model solution with the interest rate unchanged from the period before the forecast is made. In other words, the forecast does not take into account the reaction function. For the first few quarters ahead, this inconsistency has little practical significance, given the lags in the effects of monetary policy. But, as de Brouwer and O'Regan acknowledge, for forward-looking rules looking further ahead, it means that the forecasts become seriously biased and this reduces the effectiveness of the forward-looking rule. The results presented in BMR and Figure 3 suggest that when the forecasts take into account the effects of policy, much longer leads are optimal, and these substantially improve the performance of forward-looking inflation-only rules.
Credibility and the effects of price-level control
The usual argument against a price-level rule is that if it is costly to fight against inflation shocks, it will be costlier still to return the price level to a predetermined path. This standard argument, however, does not allow for possible changes in the way expectations are formed in response to the implied change in the properties of prices and inflation. With an element of price-level control, there would be an expectation of reversion to the (trend) stationary path for the price level, so that expectations of inflation rates would change sign more quickly. This would tend to make it easier for the monetary authority to control inflation.
Expectations are adaptive in de Brouwer and O'Regan's analysis, so agents in their model take no account of the important change in regime associated with a move to price-level control. Had expectations adjusted to reflect this regime shift (and the price-level rule was forward-looking), the price-level rule would, I think, have done much better, and possibly better than the alternatives.
In BMR, we examined the role for a price-level condition as part of a policy of price stability by adding a price-level gap term to the forward-looking inflation-only reaction function that generated point A in Figures 2 and 3. Specifically, we considered reaction functions of the form
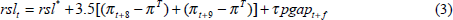
where pgapt+f is the expected difference between the f-quarter-ahead level of prices and the price-level target path, where the price-level target path is defined as the level of prices that is implied by a constant rate of inflation of πT from some given starting point. For the results presented here, f is fixed at six since this lead produces the most interesting results. Note that this reaction function reduces to an inflation-only rule with τ, the weight on the price-level gap, set to zero. Thus, the effects of adding an element of price-level control are considered on the margin.
As a first, and admittedly arbitrary, way of adjusting expectations to reflect the impact that the introduction of a price-level controller might have, we modified the equations for expected inflation in the model by including the current pgap term with a small negative coefficient. The effect of this term is to reduce expected inflation on the margin when the current price level is above its target, and increase expected inflation when the price level is currently below its target.
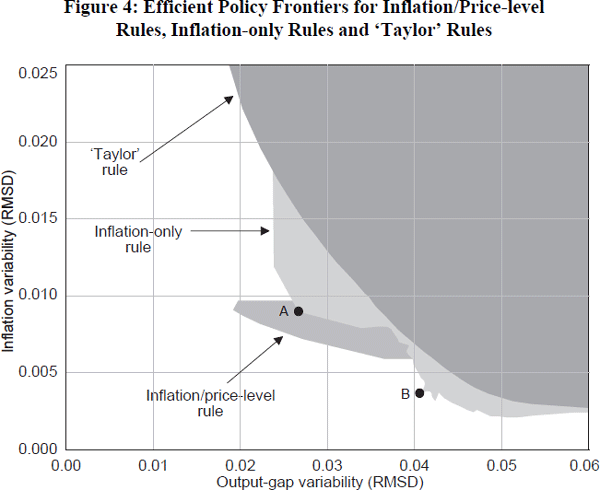
The results of this exercise are shown in Figure 4. As shown, introducing an element of price-level control opens up a new region with lower variability of both inflation and output. Note also, we have not re-optimised the inflation-only part of the reaction function, so it may well be possible to get even closer to the origin. In addition, as shown in BMR, when no adjustment is made to expectations to take account of the new emphasis placed on price-level control, the inflation/price-level rule does not produce points that are better than those for the inflation-only rule. So adjusting expectations is the key. This highlights the importance of accounting for the Lucas critique. It also highlights the need to better understand how expectations might in fact adjust.
In closing let me try and pull these thoughts together. Given the lags in the effects of changes in interest rates, monetary policy has to be forward-looking to be effective. Taylor-style rules perform reasonably well because the current state of excess demand is a good leading indicator of inflation, but explicit forward-looking rules will, in general, do even better. Of course, using an explicitly forward-looking rule requires a forecast of the variables in the rule, and this introduces an additional element of uncertainty into the policy-setting problem. This uncertainty should be taken account of in the policy process, but this does not mean that policy rules should be restricted to using only lagged variables. Rather it means that the policy response should be adjusted appropriately to reflect the type and the degree of uncertainty. In particular, if uncertainty enters multiplicatively, you may want to proceed more cautiously than the efficient forward-looking rule suggests, but you will still want to use the information in the forward-looking rule. To expand on de Brouwer and O'Regan's own metaphor, if you are driving a car and the road ahead is foggy, you may want to drive more slowly, but you are still going to look primarily through the front windshield as opposed to the rear-view mirror.
De Brouwer and O'Regan have provided a very interesting and careful analysis of alternative policy rules in the Australian context, as well as some useful experiments regarding the effects of credibility in the context of the Taylor rule. I hope this research on policy rules continues. My message is that I hope future research includes more emphasis on explicitly forward-looking rules, and, among these, rules with an element of price-level control deserve particular attention.
Footnotes
The views in these comments are my own and do not necessarily reflect those of the Bank of Canada. I am grateful to Hope Pioro for valuable technical assistance with the simulations presented herein. [*]
I put Taylor in quotes, since once leads are used in the reaction function I think it is stretching things to call this a Taylor rule. In my remarks, a Taylor rule will refer to the case using either contemporaneous values (or one lag if those contemporaneous values are viewed as being unavailable as in de Brouwer and O'Regan). [1]
I use the word ‘fully’ model consistent to indicate that it takes into account the effects of current and future monetary-policy actions. De Brouwer and O'Regan's forward-looking experiments use the model solution for the inflation rate with the interest rate held fixed at its pre-forecast setting. [2]
References
Ball, L. (1997), ‘Efficient Rules for Monetary Policy’, NBER Working Paper No. 5952.
Black, R., T. Macklem and D. Rose (1997), On Policy Rules for Price Stability, paper presented at Bank of Canada Conference, ‘Price Stability, Inflation Targets and Monetary Policy’, Bank of Canada, 3–4 May.
Svensson, L.E.O. (1997), ‘Inflation Forecast Targeting: Implementing and Monitoring Inflation Targets’, European Economic Review, 41(6), pp. 1111–1146.
2. General Discussion
Two issues were the focus of discussion in this session:
- the appropriate weights on output and inflation in a Taylor rule; and
- the appropriate way to model inflation expectations.
Some participants thought that it would be interesting to know what weights on the output gap and inflation in the Taylor rule best summarised recent Australian monetary policy. It was noted that analysis in the United States has suggested that a reasonable characterisation of the Taylor rule in that country has weights on the output gap and the deviation of inflation from target of 0.5 and 0.5. These are considerably less than the efficient weights derived in this paper, which tend to lie around 1 for both variables. It was pointed out that simple policy rules estimated using Australian data are very sensitive to the time period over which the rules are estimated and assumptions about the target rate of inflation in the 1980s and early 1990s. Furthermore, a number of participants cautioned that, while Taylor rules may be a useful way to describe history, one should be careful about interpreting them as optimal policy rules.
There was general discussion about the authors' use of backward-looking expectations but forward-looking policy rules. It was argued by some that if forward-looking expectations were used in the empirical analysis in the paper, then the differences between the various monetary-policy rules would diminish. Despite this, there was support for modelling some degree of backward-looking behaviour into inflation expectations, as this seemed to be a reasonable approximation of reality. One suggestion was to model expectations as a weighted average of a backward- and forward-looking component.
It was noted that even this approach has its difficulties. In Australia, estimating an equation for the backward-looking component of inflation expectations is complicated by the changes in the monetary-policy regime. These changes should have altered the way inflation expectations are formed. A possible solution would be to allow time-varying coefficients on the backward- and forward-looking expectations components. It was suggested that the role of learning is important in this regard, and could perhaps be built into the modelling exercise. Learning by the policy-makers is also important. In the real world, there is uncertainty regarding the structure of the economy, the neutral real interest rate and the size of the output gap. One suggestion for further research was modelling how this uncertainty affects the various policy rules.
Some speakers expressed concern that the rules discussed in the paper implied an unrealistic degree of policy activism, and that the more forward-looking was policy, the more activist policy became. In response, it was noted that, in reality, policy-makers are likely to use these rules as broad cross-checks against their judgments about the correct setting of monetary policy. In a sense the use of the word rules to describe this approach to setting interest rates is confusing, as few would advocate setting policy in strict accordance with some form of fixed Taylor rule.