RBA Annual Conference – 1997 Discussion
1. David E. Lindsey[*]
I am pleased to discuss the paper on interest-rate smoothing by Lowe and Ellis. The authors have produced a paper notable for its insightful design and thoughtful execution. This paper, together with the companion piece by de Brouwer and O'Regan, represents frontier research on the issues currently being investigated, and with the advanced techniques currently being applied, in academia as well as by staff at the Board of Governors of the Federal Reserve System. Indeed, some of my comments are intended to compare the results of the most recent of this work in the United States with results presented at this conference.
The bulk of my comments will be directed to the fourth section of the paper, which reports on econometric model simulations. As for the fifth section, I agree with the authors' balanced interpretation of the empirical evidence on whether the effects of interest-rate changes on consumer sentiment are linear and on whether interest-rate reversals have a greater impact on bond yields than equal-sized continued changes in the same direction. Also, their discussion on communication issues is useful.
Turning to their main model-simulation results, Figure 2 and Table 3 show the effects of varying the weights on the output gap, the inflation gap, and the change in the official interest rate in the policy-maker's loss function. This optimal-control exercise suggests that some degree of interest-rate smoothing can be introduced at little initial cost in terms of enlarged deviations of output and inflation from target values.
This specific loss function, which penalises variation in the official interest rate as well as inflation and output gaps, has become standard and well captures the evident preferences of central banks to smooth official interest rates. I will appeal later to just such a loss function to rationalise my proposal to respecify the backward-looking Taylor rule in a way that also can well describe actual central bank behaviour. However, worth noting at the outset is that the theoretical justification for penalising the change in the official short-term nominal interest rate in the loss function is not so clear. In terms of effects on either financial or real behaviour, why should it not instead be the change in the short real rate that enters the loss function? To be sure, as a practical matter, these nominal and real rates are highly correlated in the short run. Perhaps the evident concern of central banks for smoothing the nominal – rather than real – short rate is simply because that is the rate central banks target, and quite visibly so.
The optimal control exercise presented by Lowe and Ellis is precisely the procedure that Blinder (1997), the previous Vice Chairman of the Federal Reserve Board, advocates for practical policy-making: that is, the Federal Open Market Committee (FOMC) at each meeting should work out not only the optimal current setting for the federal funds rate, but also the currently estimated optimal planned path for that rate over an extended horizon, with both based on an explicit long-term macroeconomic forecast. Then, at the next meeting, the whole procedure should be updated reflecting new information. He criticises the FOMC for not in fact determining an optimal plan for the funds rate and for not considering a forecast extending far enough into the future.
As well exemplified by the present paper by Lowe and Ellis, the optimal-control exercise is a very productive technique for researchers to apply in addressing certain subjects. However, as a framework for actual policy-making, in my view it has fatal shortcomings. In the eyes of a practical policy-maker, the prescribed setting of the nominal short rate that is generated by the optimal-control exercise has the appearance of coming out of a ‘black box’. Explaining to men and women of affairs the rationale for a given optimal setting of the short rate is difficult. This is precisely why using approximations such as Taylor-type rules as policy guideposts has gained in popularity. This consideration is why the appearance of the efficient Taylor-rule frontier on Figure 2 of the Lowe and Ellis paper is welcome. Knowing how good a job the backward-looking Taylor rules can do compared with optimal policy-making is of considerable interest.
The prescribed interest rate derived from a backward-looking Taylor rule has a transparency, and a plausible rationale, that the one coming from a complicated optimal-control exercise inherently lacks. This transparent character also applies to forward-looking Taylor rules that rely on forecasted rather than observed output and inflation gaps to derive the prescribed short rate. Such simple rules can incorporate the complicated, resource-intensive effort central banks actually undertake in constructing macroeconomic forecasts. So the question becomes how well can forward-looking Taylor rules do in model simulations relative both to backward-looking Taylor rules and to optimal policy? The results for forward-looking Taylor rules are shown in the paper by de Brouwer and O'Regan. In addition, Lowe and Ellis use their loss function, which penalises interest-rate variation, to assess the simulated performance of a variety of these forward-looking Taylor rules.
This observation brings me to some suggestions for extensions of this type of experiment in the next stage of research by the authors of these two companion papers. First, calculating the results of forward-looking Taylor rules based on model forecasts that are consistent with the actual implementation of those rules themselves could be worthwhile. That is, each rule could be appended to the model and then all the equations of the expanded model could be solved simultaneously.
Second, a nominal short rate lagged one period with its own coefficient could be added to the specification of each forward-looking Taylor rule examined.[1] This additional term could allow the researcher to vary a coefficient that directly captures the degree of interest-rate smoothing in a manner analogous to the initial investigation by Lowe and Ellis of the effects of varying the coefficient on the change in the nominal rate in the loss function. For example, one could examine forward-looking Taylor rules with substantial long-run responses to the forecasted inflation and output gaps but with a relatively large coefficient on the lagged interest rate, making policy reactions relatively unresponsive – and hence interest rates relatively smooth – in the short run.
Such a specification can be derived from a simple theoretical model with a conveniently chosen lag structure.[2] In such a model, the multi-period loss function used by Lowe and Ellis collapses into a single-period expression for the loss whose first-order condition for minimisation can be expressed as a forward-looking Taylor rule with a lagged dependent variable.
Specifically, the lag structure in each of the two equations in the model examined in Ball (1997) can be adjusted by no more than one period to obtain this result. First, lengthen the lag in the effect of the real interest rate on the output gap in his dynamic IS curve to derive
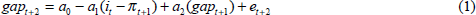
where gap = 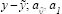 and a2
are known positive parameters with a2 less than 1; and
e is a random error term. Next, shorten the lag in the effect of the
output gap on the rate of inflation in his accelerationist Phillips curve to
derive
and a2
are known positive parameters with a2 less than 1; and
e is a random error term. Next, shorten the lag in the effect of the
output gap on the rate of inflation in his accelerationist Phillips curve to
derive

where b is a known parameter and u is a random error term.
Because the nominal official interest rate, it, in this model specification directly affects only πt+2 and gapt+2, the loss function considered by Lowe and Ellis in effect collapses to
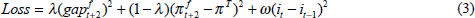
where f stands for the central bank's forecast.
Substituting Equations (1) and (2) into (3), differentiating with respect to it, setting the result equal to zero, and solving for it yields a forward-looking Taylor rule that includes a one-period lag on the it term,
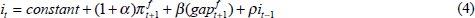
where these coefficients incorporate all the parameters in Equations (1), (2) and (3). They are positive, with ρ less than 1. In other words, in such a simple model, the optimal policy setting would correspond exactly to a Taylor rule based on the central bank's one-period-ahead forecasts of both inflation and the output gap and on the lagged value of the official rate.
To be sure, this specific, simple lag structure does not characterise either the ‘real world’ or the econometric model of Australia simulated in these two companion papers. But extensions along these lines of the experiments conducted in the papers by de Brouwer and O'Regan and by Lowe and Ellis would be valuable because they could show just how closely different forward-looking Taylor rules embodying interest-rate smoothing could approximate optimal policy in model simulations.
This brings me back to the basic issue of interest-rate smoothing. Following the
classic analysis of Brainard (1967), as re-emphasised by Blinder (1995), ‘multiplier’
uncertainty about the impact of a policy action on the economy could justify
the kind of policy-maker caution that is embodied in the interest-rate smoothing
behaviour we have been discussing. However, uncertainty about the exact location
of the non-accelerating inflation rate of unemployment (NAIRU), and thus of
potential output, which has been so much discussed in the US media of late,
ironically is the kind of additive uncertainty that in theory would not induce
partial adjustment of the policy rate with a quadratic loss function as assumed
in Equation (3). Instead, if there were no uncertainty about the parameters
a1, a2 and b in Equations
(1) and (2) above, the policy-maker could impound the terms involving potential
output, 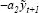 and
and 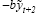 , into the intercepts
of Equations (1) and (2), respectively, indicating that mis-estimates of the
values of potential output represent additive errors. Thus, the policy-maker
would simply use the best possible available estimate of potential output for
calculating and forecasting the output gap in
Equations (1) and (2), and proceed to solve for the optimal official
rate with no support at all from Brainard for smoothing interest rates. On
the basis of this type of macro-analytics, I infer that what underlies the
penchant for interest-rate smoothing by the world's central banks must
be either uncertainty about the behavioural parameters of the economy's
structural equations or other reasons – perhaps those related to communication
and accountability discussed by Lowe and Ellis.
, into the intercepts
of Equations (1) and (2), respectively, indicating that mis-estimates of the
values of potential output represent additive errors. Thus, the policy-maker
would simply use the best possible available estimate of potential output for
calculating and forecasting the output gap in
Equations (1) and (2), and proceed to solve for the optimal official
rate with no support at all from Brainard for smoothing interest rates. On
the basis of this type of macro-analytics, I infer that what underlies the
penchant for interest-rate smoothing by the world's central banks must
be either uncertainty about the behavioural parameters of the economy's
structural equations or other reasons – perhaps those related to communication
and accountability discussed by Lowe and Ellis.
I would now like to strike a bit of a discouraging note, not about this excellent paper's analysis of monetary-policy rules incorporating interest-rate smoothing per se, but rather about the prospects for getting definitive results from the massive worldwide research effort of which this paper is a part. My perspective stems partly from the model-specific nature of the results presented, which Lowe and Ellis readily acknowledge. It also stems partly from the widely differing results Williams (1997) recently has obtained from simulations of the Federal Reserve Board's newly installed large-scale US macroeconomic model, depending on whether he assumes that the public has adaptive or rational expectations.[3]
Williams shows that in models with adaptive expectations, an interest-rate-change rule, in which the coefficient on the lagged interest rate is 1, performs relatively poorly, a result also uncovered by de Brouwer and O'Regan in their Australian model simulations. Similarly, pure price-level rules also perform relatively poorly in both studies, as do rules tied to nominal income.[4]
These results are essentially overturned in Williams' (1997) simulations of the large-scale model with gradual adjustment of the inflation rate but with rational expectations on the part of the public that incorporate all the behavioural equations in the model, including the policy rule. Although switching from adaptive to rational expectations should change the results somewhat, as was previewed in the tests of credibility effects in wage setting by de Brouwer and O'Regan, the reversal of relative rankings in Williams' 1997 paper came as a surprise to me. He finds that interest-rate-change rules, even when applied to pure price-level or nominal-GDP-level targets, not only come much closer to the frontier measuring the variation of inflation and output gaps than do conventional rules involving the interest-rate level, but they also do so with much less variation in interest rates than those conventional rules.[5]
He also shows that the coefficients of these rules can be adjusted to smooth interest rates even further at very little cost in terms of the movement away from the inflation/output variability frontier.[6] This conclusion about the low cost of interest-rate smoothing for nearly optimal policies in the context of a large-scale US model assuming rational expectations is a tantalising echo of the primary results found by Lowe and Ellis in a smaller model of the Australian economy that embodies adaptive expectations. On that crucial point of agreement, I can reach the following conclusion: once central banks around the world determine how their economies really work and how to structure appropriately their basic reaction to economic developments, then they certainly can smooth interest rates somewhat as their reward!
Footnotes
The views presented are those of the author and do not necessarily represent those of the Board of Governors of the Federal Reserve System or other members of its staff. [*]
Forward-looking Taylor rules with a one-period lag on the dependent variable were successfully estimated using regression analysis by Clarida, Gali, and Gertler (1997a) for the United States, and Clarida, Gali, and Gertler (1997b) for Germany, the United States, and Japan. Tetlow and von zur Muehlen (1996) simulate a backward-looking Taylor rule with a one-period lag on the dependent variable in a small US model with rational expectations. [1]
I am indebted to Athanasios Orphanides for this analysis. [2]
This model is described in Brayton and Tinsley (1996), Brayton, Levin, Tyron and Williams (1997), and Brayton, Mauskopf, Reifschneider, Tinsley and Williams (1997). [3]
Ball (1997) recently has stressed the problem of cycles for nominal-GDP rules in models with adaptive expectations, which is reminiscent of the warning of Anderson and Enzler (1987) about k-per cent money-growth rules in models with adaptive expectations. [4]
This result is intriguing given the potential in rational expectations models for the public in effect to perceive a policy with excessive interest-rate smoothing as likely to fall ‘behind the curve’, so that the public's model-consistent expectations in principle could contribute to cyclical instabilities. [5]
Williams also finds that a Henderson-McKibbin (1993) variant of a backward-looking Taylor rule – with coefficients of 1 and 2 on the lagged inflation and output gaps, respectively, as opposed to Taylor's 0.5 and 0.5 – comes much closer to the inflation gap/output gap variability frontier than does the Taylor rule with either rational or adaptive expectations. This Henderson-McKibbin rule in both cases, however, exhibits noticeably more interest-rate volatility. This Henderson-McKibbin rule also outperforms the Taylor rule starting from a steady state in Levin (1996) in simulations of the Federal Reserve Board's large-scale multi-country model with either adaptive or rational expectations, and in Orphanides et al. (1997) in simulations of a small model with rational expectations. The last article also uses stochastic simulations to evaluate the ‘opportunistic’ approach to attaining price stability, as discussed in Orphanides and Wilcox (1996). [6]
References
Anderson, R. and J.J. Enzler (1987), ‘Toward Realistic Policy Design: Policy Reaction Functions that Rely on Economic Forecasts’, in R. Dornbusch, S. Fischer and J. Bossons (eds), Macroeconomics and Finance: Essays in Honor of Franco Modigliani, MIT Press, Cambridge, Massachusetts, pp. 291–330.
Ball, L. (1997), ‘Efficient Rules for Monetary Policy’, NBER Working Paper No. 5952.
Blinder, A.S. (1995), ‘Central Banking in Theory and Practice, Lecture I: Targets, Instruments, and Stabilization’, Marshall Lecture presented at the University of Cambridge.
Blinder, A.S. (1997), ‘Distinguished Lecture on Economics in Government: What Central Bankers Could Learn from Academics – and Vice Versa’, Journal of Economic Perspectives, 11(2), pp. 3–19.
Brainard, W. (1967), ‘Uncertainty and the Effectiveness of Policy’, American Economic Review, 57(2), pp. 411–425.
Brayton, F., A. Levin, R. Tryon and J.C. Williams (1997), ‘The Evolution of Macro Models at the Federal Reserve Board’, Board of Governors of the Federal Reserve System, Finance and Economics Discussion Series No. 97-29.
Brayton, F., E. Mauskopf, D. Reifschneider, P. Tinsley and J.C.Williams (1997), ‘The Role of Expectations in the FRB/US Macroeconomic Model’, Federal Reserve Bulletin, 83(4), pp. 227–245.
Brayton, F. and P. Tinsley (1996), ‘A Guide to FRB/US: A Macroeconomic Model of the United States’, Board of Governors of the Federal Reserve System, Finance and Economics Discussion Series No. 96-42.
Clarida, R., J. Gali and M. Gertler (1997a), ‘Monetary Policy Rules and Macroeconomic Stability: Evidence and Some Theory’, mimeo.
Clarida, R., J. Gali and M. Gertler (1997b), ‘Monetary Policy Rules in Practice: Some International Evidence’, mimeo.
de Brouwer, G. and J. O'Regan (1997), ‘Evaluating Simple Monetary-policy Rules for Australia’, paper presented at this conference.
Henderson, D. and W.J. McKibbin (1993), ‘A Comparison of Some Basic Monetary Policy Regimes for Open Economies: Implications of Different Degrees of Instrument Adjustment and Wage Persistence’, Carnegie-Rochester Conference Series on Public Policy, 39, pp. 221–317.
Levin, A. (1996), ‘A Comparison of Alternative Monetary Policy Rules in the Federal Reserve Board's Multi-Country Model’, BIS Conference Papers, Volume 2, pp. 340–366.
Lowe, P. and L. Ellis (1997), ‘The Smoothing of Official Interest Rates’, paper presented at this conference.
Orphanides, A., D.H. Small, V. Wieland and D.W. Wilcox (1997), ‘A Quantitative Exploration of the Opportunistic Approach to Disinflation’, Board of Governors of the Federal Reserve System, Finance and Economics Discussion Series No. 97-37.
Orphanides, A. and D.W. Wilcox (1996), ‘The Opportunistic Approach to Disinflation’, Board of Governors of the Federal Reserve System, Finance and Economics Discussion Series No. 96-24.
Tetlow, R. and P. von zur Muehlen (1996), ‘Monetary Policy Rules in a Small Forward-Looking Macro Model’, Board of Governors of the Federal Reserve System, mimeo.
Williams, J.C. (1997), ‘Simple Rules for Monetary Policy’, Board of Governors of the Federal Reserve System, Finance and Economics Discussion Series (forthcoming).
2. General Discussion
The rationale for interest-rate smoothing was the main topic of discussion.
While most participants thought that frequent and large changes in interest rates were undesirable, this view was not shared universally. There was also no agreement as to why smoothing was justified. While variability in inflation and output have social costs, and so are clearly of concern to central banks, the social costs of interest-rate volatility – and hence the reason(s) why interest-rate changes should be in the central bank's loss function – are much less clear. A number of participants suggested that if volatility in official interest rates is costly, then these costs should be included in the model of the economy, rather than simply included in the central bank's loss function. It was argued that this approach might also allow empirical work to examine whether these costs actually exist.
It was noted that, to date, there had been few serious attempts to model these costs. Like this paper, most modelling work around the world suggests that interest rates should be changed by larger amounts, and more often, than occurs in practice. A number of participants agreed that frequent changes in the direction of interest rates were costly and that this provides a partial explanation for smoothing. Financial markets look to central banks for guidance about the path of the economy, and this guidance may be lost if central banks were frequently reversing the direction of interest-rate changes. Frequent changes in the direction of policy may also lead people to think that the central bank had ‘lost the plot’, although on this subject there was a variety of opinion. Some appealed to the Lucas critique, arguing that if the policy regime changed and people understood the change, then expectations as to what constituted ‘normal’ central bank behaviour would also change, eliminating the costs of volatility. In response, others argued that regardless of whether or not financial-markets participants understood the central bank's operating procedures, considerable interest-rate volatility would have adverse consequences for business investment and consumer confidence.
The discussion highlighted that judgments regarding the optimal size of interest-rate changes are complicated by the difficulties in calibrating the effects of changes in official interest rates on financial prices and the economy in general. One participant recalled the 1994 experience in the United States, where a small rise in short-term interest rates induced large movements in long-term yields. Similarly, econometric analysis identifies an ‘average’ effect of policy on activity and inflation, but economists and policy-makers do not think that the economy responds the same way to each change in interest rates.
Discussion of interest-rate smoothing raised a number of other issues for further consideration. Does smoothing of official interest rates mean that the exchange rate is more variable? Should policy aim at smoothing nominal or real interest rates? Would greater volatility in short-term interest rates imply greater volatility in longer-term interest rates, and which of these is more costly? Should policy-makers be concerned about the greater persistence of inflation and business cycles that is induced by interest-rate smoothing?