RBA Annual Conference – 1997 Evaluating Simple Monetary-policy Rules for Australia Gordon de Brouwer and James O'Regan[*]
1. Introduction
Generally, the ultimate objectives of monetary policy are low and stable inflation and maximum sustainable economic growth. Central banks have increasingly sought to achieve these goals through the formulation of formal inflation targets. In pursuing such a target, most central banks use an overnight interest rate as the instrument of policy, but exactly how the instrument should be moved to achieve the objectives of policy is an issue of active debate. A number of simple interest-rate feedback rules have been proposed to assist in setting the overnight interest rate.
The aim of this paper is to analyse these rules in a simple but data-consistent framework of the Australian economy. We do this by trying to answer a number of questions. What sort of simple policy rule – for example, an inflation-only rule, Taylor rule or nominal-income rule – performs best? Given that the economy is subject to a variety of shocks, how much can policy stabilise the economy, and how steep is the trade-off between the variability of inflation and output? How do policy rules vary with changes in inflation expectations induced by the inflation target itself? Do simple rules which also let policy respond to other variables perform better than simple rules based on inflation and output alone? Finally, should policy rules be based on actual or expected values of the target variables?
The structure of the paper follows these questions. Section 2 reviews some terminology about feedback rules, and presents a simple empirical framework of the Australian economy which is used for analysis. Section 3 evaluates several interest-rate rules, and explores the properties of what appears to be the most efficient of these, the Taylor rule. Section 4 addresses how greater credibility can affect price-setting behaviour, and what this may mean for the economy and monetary policy. Section 5 examines whether information in addition to inflation and output improves the rule. Section 6 examines whether forward-looking, rather than backward-looking, rules more successfully stabilise the economy. The findings of the paper are summarised in Section 7.
2. Some Preliminaries
2.1 The use of simple rules
The focus in this paper is on simple interest-rate rules.[1] More generally, monetary-policy rules can focus on a number of financial variables, such as the short-term interest rate, money, credit or the exchange rate. Given that the operating instrument in Australia is the cash rate, however, it is natural to restrict analysis of rules to the overnight nominal interest rate. Moreover, as Edey (1997) argues, other financial variables do not seem to be viable instruments for Australia.
A simple rule is a reaction function, according to which policy is changed in response to the values of a few key variables. While a rule prescribes a certain course of action for policy, it is up to policy-makers whether they follow it or not. There have been proposals at various times for central banks to be bound by such rules – like Friedman's constant money-growth rule – but these are not practical since both the economy and policy are too complex to be summarised in a simple rule. Rather, the prescription provided by a rule can be thought of as a guide for policy-makers in setting the policy instrument.
The simple interest-rate rules examined in this paper are assessed with the aim of finding which rule, and what sort of reaction coefficients in a rule, are most efficient. Since stabilisation policy generally means maintaining low and stable inflation and keeping output at its potential, it is natural to define efficiency in terms of reducing the variability in inflation and the output gap as much as is possible. Accordingly, a policy rule is said to be efficient if the variability of either inflation or the output gap is minimised given the variability of the other. For any given rule, different reaction coefficients can yield different combinations of variability in inflation or output, so there is a frontier of efficient rules.
As explained in Section 3.1, we explore the properties of simple rules by assessing outcomes for a range of values for the reaction coefficients. Since this procedure is not based on the preferences of the monetary authority, the simple rule only reveals the possibilities for the trade-off between inflation and output variability, not which possibility is preferred. Furthermore, since the procedure does not use a maximisation routine, the efficient rules do not necessarily represent the technically best outcomes.[2]
2.2 A stylised representation of the Australian economy
In analysing empirical policy rules it is necessary to have a view on the basic structure of the economy and on how monetary policy affects it. The results depend, of course, on the structure used for analysis. In the simple framework used here, there are five endogenous variables (non-farm output, prices, unit labour costs, the real exchange rate and import prices), five exogenous variables (world output, world prices, the terms of trade, the world interest rate and domestic farm output) and one control variable (the short-term nominal interest rate). While the full set of estimated equations and data are listed in Appendix 1, the equations for the key endogenous variables may be summarised as:


where y is non-farm output, tot is the terms of trade, rtwi is the real exchange rate in terms of domestic currency (so a rise is an appreciation), fy is farm income, r is the real interest rate, p is the price level, ulc is unit labour costs, ip is import prices in domestic currency, gap is actual output less potential and an asterisk denotes a foreign variable.[3]
In the long run, Australian output is determined by foreign output (through demand and supply effects), the terms of trade and the real exchange rate (Equation 1).[4] To the extent that the real exchange rate is itself determined by the terms of trade (Equation 4), the effect of the latter two variables on output tends to net out, and so Australian output depends on foreign output. Output falls below its long-run path when the real interest rate lies above the so-called policy-neutral rate, which is the real rate when output is at potential and inflation is stable at the desired rate. This implies that in the notional long run, monetary policy does not have real effects. Monetary policy is assumed to affect activity over a period of time. Growth in farm output also has short-run effects on non-farm growth.
Consumer prices are modelled as a mark-up over import prices and unit labour costs, with the mark-up varying over the cycle (Equation 2). Import prices are affected by movements in world prices and the nominal exchange rate, with gradual, but eventually complete, pass-through. World prices are exogenous to a small economy like Australia, but the exchange rate is not. While the nominal exchange rate is unpredictable in the near-term, over longer periods of, say, quarters and years, it is fairly well explained by inflation differences between countries, the terms of trade and the real short-term interest differential (Equation 4). (Since the real exchange rate also enters the output equation, it provides a link between the real cash rate, output and inflation.) The other fundamental determinant of inflation is unit labour costs, or wages adjusted for productivity. Productivity growth is assumed to be constant, so growth in unit labour costs is synonymous with growth in wages. The empirical regularity has been that unit labour costs can be explained by recent past inflation and the recent strength of demand, but not by much else (Equation 3).[5] Both prices and unit labour costs are responsive to lags of the output gap.
Foreign output, foreign prices, farm output, the terms of trade and world real interest rates are exogenous in this system, and are modelled as univariate time series.
This stylised representation of the economy embodies a simple transmission process. The policy instrument is the nominal cash rate. Monetary policy reduces inflation by generating an output gap and an appreciation of the exchange rate. A rise in the nominal interest rate raises the real interest rate which affects output indirectly through the real exchange rate and directly through other mechanisms (Grenville 1995), generating downward pressure on wages and inflation. The appreciation of the nominal exchange rate induced by higher local interest rates also directly lowers inflation by reducing the Australian dollar price of imports. The initial effects of policy on inflation are through the exchange rate, with the output effects taking a relatively long while to feed through.
It is assumed that there is simple feedback between wages and prices. A positive ‘shock’ to wages is transmitted to prices, fed back into wages and so on. Price and wage inflation rise to a new level unless there is an offsetting negative shock or unless the gap between actual and potential output widens. An offsetting negative shock in this case would be a tightening of wages policy, as occurred, for example, under the Accord. A widening of the gap is effected by a tightening of monetary policy.
3. Which Simple Rule is Best?
There is a menu of rules for policy-makers to choose from, but some perform better than others. This section evaluates the most commonly discussed rules, and then examines the best of these in some detail.
3.1 Evaluating rules
The seven nominal-interest-rate rules evaluated are:
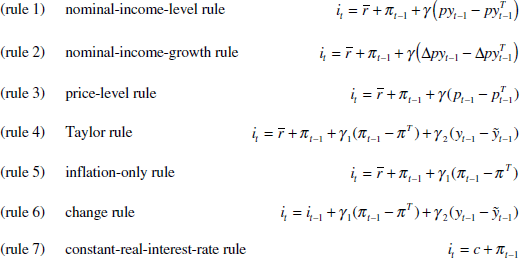
where i indicates the nominal interest rate,  the neutral real
interest rate, π the inflation rate over the past year, py
nominal income, superscript T a target, p the price level,
y real income,
the neutral real
interest rate, π the inflation rate over the past year, py
nominal income, superscript T a target, p the price level,
y real income,  potential output,
c an unspecified constant real interest rate, and γ
a reaction parameter.
potential output,
c an unspecified constant real interest rate, and γ
a reaction parameter.
These rules set the current nominal interest rate on the basis of currently available information. While much of the literature on policy-rule evaluation uses current-dated variables (Bryant, Hooper and Mann 1993; Henderson and McKibbin 1993; Taylor 1993; Levin 1996), the rules in this paper are assessed using variables lagged one quarter since these are the most recent data at hand. This is done in order to evaluate the rules on the same real-time basis as decisions are actually made (Stuart 1996).
The first six of these rules set the nominal cash rate in response to the deviation of a variable, or set of variables, from a target. Rules 1 and 2 respectively tie the interest rate to deviations of nominal income from a target level or target growth rate. These rules both yield the same forecasts for nominal income, but the outcomes can be quite different since a growth rule allows levels-drift, in the sense that past shocks to growth are bygones once growth is back on target. Rule 3 is a variant of Rule 1, by which policy is changed when the price level deviates from the target price level. Rule 4 is a hybrid nominal-income rule by which policy is tightened when inflation is above target and output above potential. In contrast to the nominal-income-growth rule, it is the output gap, rather than output growth, that enters the reaction function. This rule, initially developed by Bryant, Hooper and Mann (1993) but usually called a Taylor rule (Taylor 1993), is widely acknowledged to describe the variables that are of most concern to central banks. Rule 5 is an inflation-only rule, a special case of the Taylor rule when policy responds only to deviations of inflation from target. Both the Taylor rule and the inflation rule are tied to the inflation target, but the Taylor rule also responds to the output gap. Note that ‘inflation target’ and ‘inflation rule’ are distinct concepts: the former describes a policy objective, the latter a trigger for changing the policy instrument.
Rules 1 to 5 also include two other variables, the neutral real interest rate and the prevailing inflation rate. This means that if the reaction variables – nominal income, the price level, inflation or output – are at their target value, then the nominal interest rate equals the neutral real interest rate plus the inflation rate. The economy is in equilibrium, and so policy is neutral.[6] Rule 6 is a variant of the Taylor rule, by which the nominal rate is changed when inflation deviates from target and output deviates from potential. It reacts to the same target variables as a Taylor rule, but is not explicitly grounded to the neutral real interest rate.[7]
Rule 7 states that the real interest rate should be kept constant. This rule has been proposed, for example, on the view that fiscal policy should stabilise output, while monetary policy should stabilise the inter-temporal price of consumption – the real interest rate (Quiggin 1997).
Since the Reserve Bank of Australia has a formal inflation target, aimed at keeping average inflation at between 2 to 3 per cent over the course of the business cycle, the inflation target is set at 2½ per cent.[8] For comparability, the target price level in Rule 3 grows at 2½ per cent a year. Potential output grows at its average growth over the past 15 years, which is about 3 per cent a year. Target nominal income growth is about 5½ per cent a year, and, again for comparability, the target level for nominal income also grows at about 5½ per cent a year. The empirical analysis, trade-offs and discussion in this paper do not depend on the specific values of these variables. (Since the constant terms in the equations are calibrated to these values, all they do is ‘close’ the system without influencing the outcome.)
The properties of the system for different rules are explored using simulation analysis for each rule with different coefficient values in the reaction function. The initial range of values is 0 to 2 with increments of 0.1, but the increments are lowered if the system is unstable at low weights. This range encompasses the figures used in Taylor (1993) and Bryant, Hooper and Mann (1993). There are 10 equations for the five endogenous and five exogenous variables, and these are estimated from September 1980 to September 1996. The simulations for each rule and set of weights are run over 1,000 periods, using random errors for each equation which embody the historical covariance of these ‘shocks’.[9] The methodology is explained in more detail in Appendix 2. Each rule is evaluated using the same set of shocks. The shocks to the exogenous variables interact with their data-generating processes to create cycles similar to those of the past 15 years. This paper complements Debelle and Stevens (1995) which explored the trade-offs between variability in inflation and the output gap in a simpler framework.
Using the simulated outcomes, we calculate the standard deviations of the output gap and inflation for each of these policy rules. As explained above, a rule specification is efficient if it minimises the variation in the output gap, given the variability in inflation, or vice versa.[10] The efficient frontiers for the first six rules are graphed in Figure 1. The length of the efficient frontier can differ between rules. The vertical axis shows the standard deviation of annual inflation; the horizontal axis the standard deviation of the output gap.[11]
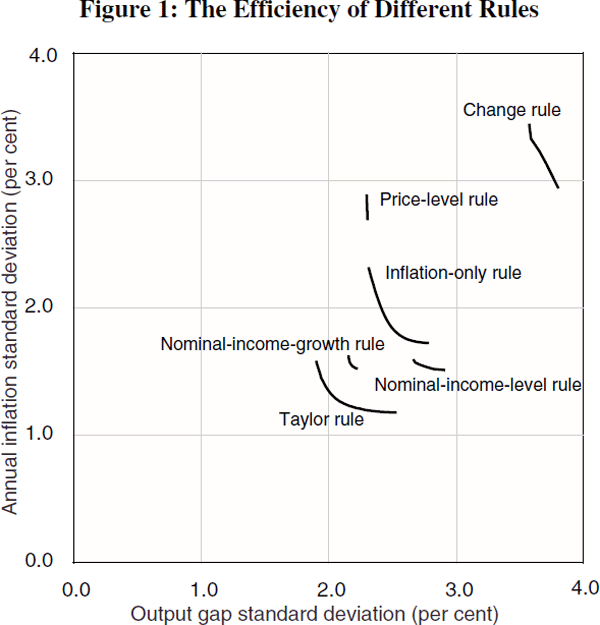
What is most striking about Figure 1 is that none of the efficient frontiers for any of the rules even gets close to reducing the variability in inflation or output to zero. There is an irreducible variability in inflation and output – policy can help minimise fluctuations in inflation and output, but it cannot get rid of them altogether. In terms of the economic framework used here, the policy rule that unambiguously does this best is the Taylor rule. But even in this case, there is still considerable variability in the economy. For example, an efficient Taylor rule keeps annual inflation within a bound of 0 to 5 per cent, or annual growth within a bound of −1 to 7 per cent, 95 per cent of the time.
The Taylor rule clearly dominates an inflation-only rule since it yields not only lower output variability, as would be expected, but also substantially lower inflation variability. In the analytical framework used in this paper, inflation is largely determined by recent domestic excess demand, either directly or indirectly through wages. As such, current demand is an important predictor of future inflation: reacting to the strength of demand now, as embodied in the output gap, lowers the overall variability of inflation. This is important. Even if a central bank cares only about inflation, it can stabilise inflation more if it responds not just to the deviation of inflation from target but also to the state of demand. This confirms Ball's (1997) analysis and is discussed in more detail in Section 3.2. (For similar reasons, a nominal-income-level rule is superior to a price-level rule.)
The change rule is stable only for a few, very low, weights on inflation and output. It is not difficult to see why. The change rule dictates that policy is continually changed until inflation is at target and output at potential, without reference to the level of the interest rate. Policy, however, operates with a lag, and so by the time inflation and output are where the central bank wants them to be, the forces are already in train to move them off. If lags are important, as the econometric evidence suggests (Gruen and Shuetrim 1994; Gruen, Romalis and Chandra 1997), then this rule is particularly undesirable since it puts policy on a knife-edge – if policy-makers make a small mistake with such a rule, putting just a little too much weight on the target variables, the system becomes dynamically unstable. This is not the case with the Taylor rule, indicating that the level of the interest rate needs to be kept in mind when interest rates are changed.
The Taylor rule is not only better than other rules which respond to deviations of inflation from target, but, at least in the framework used here, it is also superior to nominal-income rules, in either growth or levels form, and to price-level rules.[12] Consistent with Ball's (1997) model, nominal-income rules are relatively inefficient, with the efficient frontier lying outside the Taylor-rule frontier. If inflation rises, interest rates rise and output falls. As inflation is brought back to target, output should be brought back to potential, which implies that output growth is initially above trend but then stabilises at trend. A Taylor rule accommodates the initial rapid growth, since what matters is not whether growth is fast or slow, but how much spare capacity there is in the economy. A nominal-income rule, however, does not. Under a nominal-income-growth rule, for example, inflation plus the above-trend growth (which is needed to close the gap) violate the rule, and policy is tightened, pushing inflation and output down. The economy is set on an unending series of cycles. Since the lags in the system are quite long, increasing the weight on nominal income beyond the weights in the efficient frontier soon makes the oscillations unstable.
This result is at odds with much of the literature on policy modelling, which finds that Taylor rules and nominal-income rules are basically on par.[13] The difference is that expectations are adaptive in this model rather than rational as is typical in the literature. An important implication of this is that inflation is more persistent than in rational-expectations models, and this tends to improve the performance of Taylor rules relative to nominal-income rules.[14] For example, if we make expectations more forward-looking and reduce the persistence of inflation, the efficient frontiers tend to move closer to the origin for both rules, but the move is relatively larger for the nominal-income rule. This highlights that the ranking of rules can depend on how one believes the economy works. Given the strong persistence of inflation and the observation that measures of inflation expectations lag actual inflation (Fuhrer 1995; Gagnon 1997), it seems appropriate to model inflation expectations as backward-looking.
Finally, a constant-real-interest-rate rule yields one value for the trade-off between the variability of inflation and the output gap, but this point is not shown in Figure 1, as the variance of inflation is technically undefined. If the real interest rate is kept constant, monetary policy does not respond to shocks to inflation, but accommodates them. If inflation rises, for example, the nominal interest rate rises by the same amount that inflation rose by. But inflation is not brought back to where it was before the shock, since the real interest rate, which is what affects activity and the real exchange rate, is unchanged. The path of inflation depends purely on past shocks to inflation. Such a rule is clearly not viable as a means to achieve an inflation target.
3.2 Properties of efficient Taylor rules
Figure 1 shows that, for the description of the economy used here, the Taylor rule is the most efficient. This section examines the properties of this rule in more detail. Recall that the Taylor-rule frontier in Figure 1 shows outcomes from the efficient Taylor rules. Here we look at the full set of outcomes for the rule for the range of reaction coefficients on inflation and output from 0 to 2. Figure 2 sets out the different combinations of variability in inflation and the output gap associated with different weights in the Taylor rule (with the outcomes confined to standard deviations at or below 3.5 per cent).
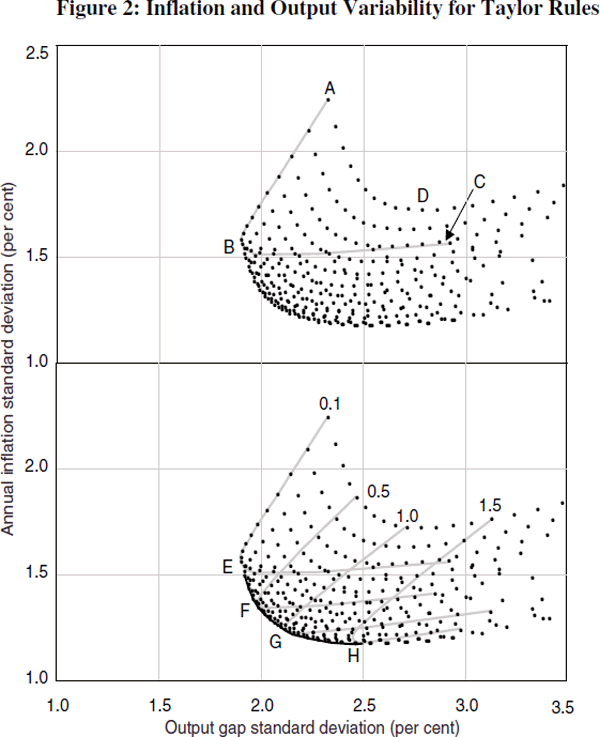
Panel 1 of Figure 2 shows the nature of the trade-offs between inflation and output-gap variability. This is repeated in panel 2, with the bottom envelope of the trade-offs constituting the efficient set shown in Figure 1. Consider point A in panel 1 where the weight on inflation is 0.1 and the weight on the output gap is zero.[15] As the weight on output is increased, with the weight on inflation kept constant, the trade-off moves down towards the origin, to point B, where the weight on output is 0.9, and then to point C. As the weight on output increases from A to B, the variability of both inflation and output falls. As argued in Section 3.1, excess demand is a key determinant of inflation, and so reducing the variability of output relative to potential helps to stabilise inflation. But there is a limit to this: if interest rates move too much in response to output, the stabilising properties of the rule are weakened, and the variability of inflation and output start to rise to point C, where the weight on output is 1.8. As shown in panel 2, this pattern is repeated when the constant weight on inflation is set higher, at, for example, 0.5, 1 and 1.5.
Analogous to the line AB, the points from A to D in panel 1 represent an increasing weight on inflation for a constant weight on output. Increasing the weight on inflation stabilises inflation but, unlike in the previous case, it increases the variability in output. While the output gap is a key predictor of inflation, in our simple framework the opposite is not true. Again, increasing the weight on inflation beyond the value associated with point D becomes counterproductive, and the variability in inflation starts to increase.
Increasing the reaction of policy to inflation and output improves stability in inflation and output, but responding too much is counterproductive. A set of efficient Taylor rules is, therefore, well defined. This is shown in panel 2 as the highlighted collection of points closest to the origin of zero. The efficient frontier minimises the variability of either inflation or the output gap given the variability of the other.
This efficient set does not generally put the economy on a knife edge where the variability of inflation and output explode when the weights are just above the efficient weights. For example, the points that follow on from the line AD in Figure 2 represent higher weights on inflation that increase the variability in inflation, but they are certainly not explosive. Only if the weights on inflation and output are both relatively high (close to 2) does variability become explosive. In other words, inflation and output are only unstable when interest rates are moved around ‘an awful lot’. Efficient Taylor rules are generally viable for policy since small mistakes do not have big consequences.
Table 1 summarises some key economic properties at different points on the efficiency frontier shown in panel 2 of Figure 2. The first column of data gives some of the actual properties over the 1990s. Then four outcomes are examined. Points E and H are the extremes of the frontier (with point E in panel 2 the same as point B in panel 1); F is the point where the sum of the variability in inflation and the output gap is minimised (that is, where the frontier is closest to the origin of zero). Point G is included so that points E through to H roughly represent equal-sized increases in the weight on inflation.
| Quarterly data | 1990s | Point E | Point F | Point G | Point H | |
|---|---|---|---|---|---|---|
| Weight | Annual inflation | 0.1 | 0.5 | 1.0 | 1.5 | |
| Output gap | 0.9 | 1.0 | 1.1 | 1.2 | ||
| Standard deviation: | Annual inflation | 1.31 | 1.58 | 1.35 | 1.22 | 1.18 |
| Output gap | 1.95 | 1.90 | 1.99 | 2.18 | 2.53 | |
| Δ cash rate | 0.73 | 0.91 | 1.06 | 1.32 | 1.71 | |
| Autocorrelation (1) | Annual inflation | 0.96 | 0.96 | 0.95 | 0.93 | 0.92 |
| Autocorrelation (2) | 0.96 | 0.91 | 0.87 | 0.82 | 0.79 | |
| Autocorrelation (4) | 0.70 | 0.76 | 0.64 | 0.52 | 0.41 | |
| Autocorrelation (1) | Output gap | 0.92 | 0.90 | 0.90 | 0.91 | 0.91 |
| Autocorrelation (2) | 0.76 | 0.74 | 0.74 | 0.75 | 0.75 | |
| Autocorrelation (4) | 0.25 | 0.38 | 0.36 | 0.33 | 0.28 | |
| Autocorrelation (1) | Δ cash rate | 0.73 | 0.29 | 0.39 | 0.50 | 0.60 |
| Autocorrelation (2) | 0.65 | 0.18 | 0.23 | 0.31 | 0.41 | |
| Autocorrelation (4) | 0.52 | −0.10 | −0.09 | −0.08 | −0.07 | |
| Δ cash rate: | Mean (absolute) | 0.60 | 0.72 | 0.85 | 1.04 | 1.36 |
| Median (absolute) | 0.50 | 0.60 | 0.70 | 0.88 | 1.11 | |
| Reversals rate (%)(a) | 0.26 | 0.43 | 0.39 | 0.35 | 0.28 | |
| |Δ| > 0.5% (%)(b) | 0.48 | 0.57 | 0.64 | 0.69 | 0.77 | |
|
Notes: (a) Per cent of observations that the sign of interest-rate changes reverses. (b) Per cent of observations that the change in interest rates exceeds half a percentage point. |
||||||
While the weight on inflation along the frontier varies from 0.1 to 1.5, the weight on output only ranges from 0.9 to 1.2 (with a mean of 1.06 and median of 1.1) in the empirical framework used here.[16] If lags are important and output helps to predict inflation, then the efficient rule puts a fairly high weight on output. Henderson and McKibbin (1993) and Levin (1996) report a similar result for large international economic models. Excess demand is an important determinant of inflation, both directly and indirectly through wages, but policy also has to respond to other systematic influences on inflation, such as effects through the exchange rate, and to inflationary shocks. The characteristics of inflation change substantially as the weight on inflation is increased. At E, for example, the weight on inflation is very low, and inflation variability and persistence high. Inflation is close to a random walk since policy hardly responds to inflationary shocks at that point. But as the weight on inflation rises, inflation variability and persistence fall.[17]
In this simple framework, the trade-off between inflation and output variability lies largely in the choice of the inflation weight in the reaction function. As in Debelle and Stevens (1995), the trade-off is convex: at relatively high levels of inflation variability, the costs to output stabilisation of moderating movements in inflation are quite small, but they get bigger and bigger as the variability in inflation falls. For example, increasing the weight on inflation by 0.1 at point E reduces the inflation standard deviation by 0.063 per cent and increases the output-gap standard deviation by 0.01 per cent, a trade-off rate of 1 to 0.15. But increasing the weight on inflation by 0.1 to arrive at point H reduces the inflation standard deviation by 0.0023 per cent and increases the output-gap standard deviation by 0.07 per cent, which is a trade-off rate of 1 to 30.
As the weight on inflation increases, the nominal cash rate becomes more variable and policy changes become bigger.[18] The fall in inflation variability associated with more weight on inflation increases the variability in the output gap, since output is not a function of inflation in this model, and so interest-rate variability has to increase. The mean absolute quarterly change of the nominal cash rate, for example, rises from about ¾ per cent to 1¼ per cent. The persistence of changes in the interest rate also increases, and the frequency of reversals declines.[19] This issue is discussed further in Lowe and Ellis (1997).
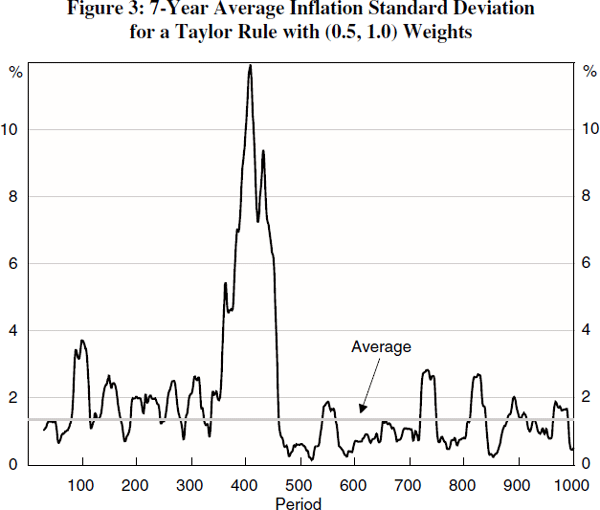
It is obvious that a simple feedback rule like the Taylor rule reduces, and does not eliminate, the amplitude of the cycles in inflation and output. The extent to which it can dampen fluctuations, however, depends on the sorts and size of shocks hitting the economy over time. It is much easier to meet an inflation target, for example, when inflationary shocks are small and offsetting. But big shocks can occur which push inflation off target. Figure 3, for example, shows the 7-year rolling standard deviation of inflation from target associated with Point F in Figure 2. A simple backward-looking rule applied mechanistically cannot ensure that inflation equals target inflation over every business cycle. This does not mean that the central bank has become less serious about inflation – the target and the responsiveness of the monetary authorities are unchanged – but shocks may be sufficiently large at some point in time as to make the target difficult to achieve in the short term.
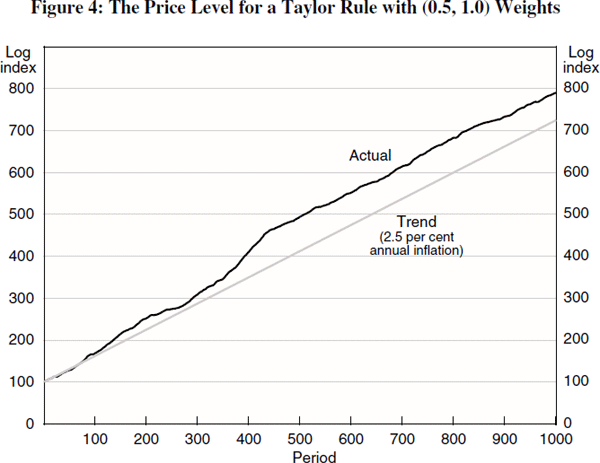
This also serves to highlight the difference between inflation and price-level rules. Given the Reserve Bank's inflation target, expected annual inflation over the course of a business cycle is 2½ per cent. Similarly, if the Bank had a price-level target by which the price level was set to grow at 2½ per cent a year, expected annual inflation would also be 2½ per cent. But the outcomes for each of these targets may well differ. In an inflation-target regime, past deviations from target are bygones. But in a price-level-target regime, past deviations from target have to be corrected. Consequently, the price level is not stationary in an inflation-targeting regime, although it is in a price-level-target regime. This is apparent in Figure 4 which shows the history of the price level associated with Point F in Figure 2. Inflationary shocks permanently change the price level under an inflation target.
3.3 The unknowns in a Taylor rule
While the Taylor rule indicates how the policy instrument should be set based on what is currently known about inflation and output, it still contains two unknowns – the ‘neutral’ real interest rate and potential output. There is, in fact, considerable debate among economists about the ‘true’ value of these variables – witness the lively argument in the United States over the past few years about potential output and the natural rate of unemployment. Indeed, these values are probably changing over time, and estimates based on econometric and episodic analysis will tend to lag reality. (This highlights that even a policy rule based on the latest data still involves a lot of judgment on the part of policy-makers.)
Consider what happens when the central bank uses the rule mechanically and under-estimates potential output. In the first place, policy is tighter than it otherwise would be, and output and inflation both fall. Since inflation is falling and an output gap is emerging, interest rates are lowered. Output is brought back to its true potential, but inflation stays lower and does not return to target, since output has gone back to true potential but not exceeded it. Interest rates are stable, however, since inflation is now lower than the target rate by the exact amount that offsets the weighted difference between true potential output and the central bank's estimate of potential output which enters the Taylor rule.[20] A similar result follows when the central bank thinks that the neutral real interest rate is higher than it actually is, and so tries to keep interest rates higher than otherwise. In short, misperceptions of the neutral real rate or potential output generate a disinflationary recession or an inflationary boom, ultimately leaving the economy in equilibrium but with a different inflation rate.
Putting a rule on auto-pilot is not viable. The appropriate response to uncertainty about the neutral real rate or potential output is to use a rule heuristically, or with learning, to find the true structure of the economy. If policy-makers' judgments are wrong, then, barring major shocks occurring at the same time, the course of output and the fact that inflation is stable but not at the target rate should tell policy-makers that they have policy too loose or too tight, and hence that they need to reassess their assumptions about the structure of the economy and the stance of policy.[21] This can be thought of as second-stage policy feedback from a policy rule. Indeed, the need to use common sense is reinforced by the likelihood that potential output and the neutral real rate are changing over time, with policy-makers striving to understand these changes.
Generally speaking, policy should not be less activist because of such uncertainty. In simulations, the response coefficients in the efficient rule do not fall as uncertainty or mistakes about potential output and the neutral real interest rate are introduced. For example, even if policy-makers persistently think that the real neutral rate is 0.5 per cent higher than its true value, or that potential annual growth is 0.5 per cent lower than its true value, the reaction weights on inflation and output in the efficient rule are very similar to before (although the overall variability of inflation and output is higher).
4. What are the Effects of Greater Credibility?
Analysis of rules using a fixed model is useful only so long as people do not substantially change their behaviour because of the operation of the rule (Lucas 1976). This applies, of course, to the results in this paper. But it is especially pertinent, since one of the primary motivations for introducing an inflation target – which underpins the Taylor rule – is that it induces a regime change by providing an anchor for inflation expectations. When an inflation target is credible, it should influence the behaviour of people, including price setters in labour, goods and financial markets.
While a credible inflation target can affect price setting in the gamut of markets, in the simple framework used here it is easiest to demonstrate what these effects may be by looking at the labour market, since this is the only market where price-setting is explicitly modelled. The analysis applies analogously to other price-setting behaviour in the economy.
Greater credibility of an inflation target can have at least three effects:
- It provides a nominal anchor for inflation expectations. An inflation target, if credible, can tie down expectations and hence prices and wages, making a reduction in inflation less costly than for simple backward-looking wage processes.
- It may reduce the number or size of ‘shocks’ since it signals a commitment by the central bank that it will not accommodate inflationary shocks. For example, if wage-setters obtain pay increases which make unit labour cost growth inconsistent with the inflation target, then the central bank is likely to tighten monetary policy. If wage-setters know this and care about employment, they will be less inclined to pursue wage increases beyond the target rate of inflation and productivity growth. There should be fewer inflationary wage pushes as a result.[22]
- It tends to lengthen contracts since it stabilises inflation at a low rate. When inflation is variable, it is costly for both employees and employers to set wages too far ahead. As the fall in inflation in the early 1990s became seen as permanent, wage contracts lengthened (Department of Industrial Relations 1996). This slows down the speed with which changes in the interest rate feed through to prices, making it longer, and harder, for policy to bring inflation back to target after a shock. But as contract periods become longer, they are also likely to become staggered, with the effect that changes in the output gap are more muted than before, and variability in wages and prices smaller.
The consequences of a credible inflation target for the trade-off between variability in inflation and the output gap in efficient Taylor rules are shown in Figure 5. The effect of anchoring inflation expectations on the target is modelled by assuming that wage-setters set unit labour cost growth based on the central bank's inflation target, rather than past inflation, and on the strength of domestic demand (panel 1). The effect of smaller wages shocks on inflation and output variability is modelled by assuming that such shocks are (arbitrarily) half as big as they were before (panel 2). The effect of longer wages contracts is modelled by (arbitrarily) splitting wage-setters into four groups whose wages stay in effect for four periods (panel 3). The variability of both inflation and output falls in all three cases.
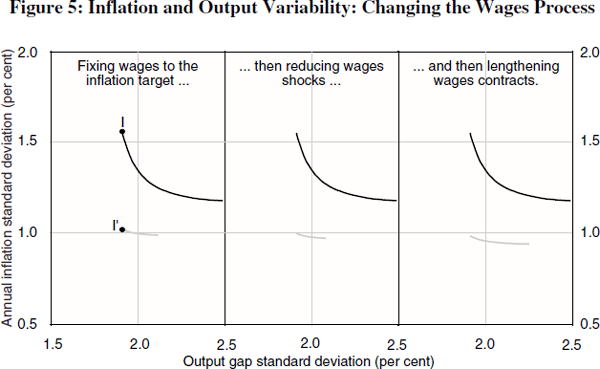
When there is full credibility, so that wage-setters decide to fix the growth in unit labour costs to the central bank's inflation target, the variability in inflation and output falls. Anchoring wages shifts the efficient frontier from the black line to the grey line in the first panel. Points I and I′ identify one point on each frontier for the same reaction function. The fall in inflation variability is striking, but perhaps not all that surprising since anchoring wages substantially reduces the variability in wages, and wages are a key part of the inflation process.
This does not mean that the output gains from credibility are negligible. Since inflation expectations do not change when inflation changes, the economy does not move onto a different short-run Phillips curve, which substantially reduces the output costs of stabilising inflation at target. This alters the trade-off between inflation and output variability, shown by the flattening of the efficiency frontier.
This has a profound implication for monetary policy: if policy is fully credible so that prices are linked to the inflation target, then policy can react more to output without compromising the commitment to low and stable inflation. Figure 6 is an enlarged version of the first panel of Figure 5. Suppose that the efficient frontier is given by the black line, and the preferences of the central bank are such that it choses point J where a one-unit reduction in inflation variability is roughly equivalent to a one-unit increase in output variability. At J, the inflation and output weights in the Taylor rule are 0.8 and 1, yielding a standard deviation in inflation and output of 1.26 and 2.08 per cent. When price-setters focus on the inflation target, rather than just past inflation, the efficient frontier shifts to the grey line. If the central bank applies similar Taylor-rule weights, it then choses point J′, with inflation and output standard deviations of 0.99 and 2.07 per cent. But the trade-off between inflation and output variability at J′ is different to J, since the slope of the efficient frontier is different. If the central bank wants to maintain the same trade-off, the best it can do is to select point K, where inflation variability is only marginally higher than at J′ (1.03 compared to 0.99) but output variability is considerably lower (1.90 compared to 2.07).
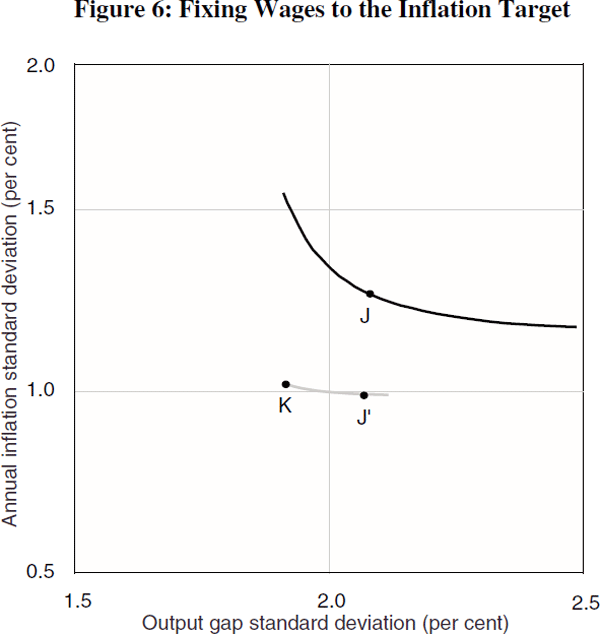
At K, the weight on inflation is lower than at J′ but the weight on output is about the same. The authorities still care about inflation variability as much as before – the slope of the trade-off has not changed – but they do not need to react to inflation as much since anchored inflation expectations partly do the job for it. At K both inflation and output variability are substantially reduced. This underscores why central banks are so concerned that price-setters know about, and focus on, their inflation targets. The gains to the community are obviously much higher when prices and wages are centred on the inflation target rather than being dependent on recent past inflation.
The second panel of Figure 5 shows that when the size of wages shocks is halved, there is a further, but modest, fall in the variability of inflation and output.
The third panel shows that lengthening contracts also improves the trade-off, since it softens the impact of output shocks on inflation variability. When wages growth is tied to the inflation target, inflation shocks are not passed on into wages and hence are not fed back into the inflation process. But output shocks are still passed on into wages since wages are sensitive to the state of the cycle. Lengthening wage contracts, however, smooths out output shocks to some degree, and so directly reduces the variability in wages and inflation and indirectly reduces the variability in output.
Putting these three effects together, the largest gains come from price-setters taking the inflation target seriously. When policy is perfectly credible and the inflation target is fixed in the minds of price-setters, there is a new dynamic in the economy which forces the inflation rate to converge back to target, reducing the variability in both inflation and output. This has an important implication for the selection of policy regimes. Rules which focus explicitly on the inflation target, like a Taylor rule, are likely to yield larger credibility gains than those that do not, like a nominal-income rule (Bernanke and Mishkin 1997). It is instructive that inflation, not nominal income, is the object of the policy-target regimes that several central banks have introduced in the 1990s. Moreover, while the issue is obviously complex, this may suggest that the preferred weight on inflation may be initially higher than otherwise in order to establish the credibility of the inflation target, and so reap the gains of greater stability in both inflation and output.
5. Is the Simple Taylor Rule Efficient in an Open Economy?
The logic of a feedback rule is that the monetary-policy instrument responds to the variables which contain the most information about the ultimate targets of policy. In the Taylor rule, the nominal interest rate reacts to the inflation rate and output gap. In a simple model of a closed economy, inflation and output are the only two variables which determine the path of inflation and output over time. Other information variables do not need to be included in the reaction function (Ball 1997). But, in principle, it may be necessary to include other variables in a simple feedback rule if they have extra information about the ultimate targets of policy. This may be the case, for example, when the economy is open – so the exchange rate, foreign financial prices and foreign output matter for domestic inflation and output – or when labour has market power in setting wages. In this case, a simple rule premised on inflation and output alone is not necessarily efficient. The extent to which reacting to other variables helps reduce the variability of inflation and output depends on how the inflation and output processes – and the system of lags in particular – are specified.
In this exercise, we examine the reduction in variability from including unit labour costs and the real exchange rate in efficient Taylor rules. In the characterisation of the economy used in this paper, these variables start to affect inflation and output almost immediately but the full effect takes a long time. This suggests that there may be some gain to including these variables in the reaction function, although the amount of the gain is an empirical issue. We examine this by calculating the change in the variability of inflation and the output gap when the deviation of unit labour cost growth from 2½ per cent (Equation 5), or the deviation of the real exchange rate from its equilibrium value (Equation 6), is included in a reaction function. The expanded Taylor rules are
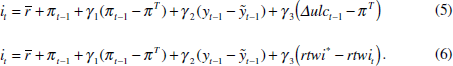
Table 2 reports results of how the efficient frontier from a simple Taylor rule can be improved by considering other sources of information about future inflation and output. The first row lists selected inflation weights, and the next two the efficient weights on the output gap and wages associated with each inflation weight. The fourth and fifth rows report the change in the standard deviation in inflation and the output gap when wages are included. A negative number means that variability is reduced. The next set of rows repeats the exercise for the real exchange rate.
| Inflation weight | ||||||
|---|---|---|---|---|---|---|
| 0.1 | 0.5 | 1.0 | 1.2 | 1.5 | 1.7 | |
| Output-gap weight | 1.1 | 1.0 | 1.1 | 1.1 | 1.1 | 1.1 |
| Wages weight | 0.19 | 0.11 | 0.05 | 0.04 | 0.00 | 0.00 |
| Δ inflation standard deviation | −0.14 | −0.05 | −0.01 | −0.00 | 0.00 | 0.00 |
| Δ gap standard deviation | 0.08 | 0.05 | 0.05 | 0.04 | 0.00 | 0.00 |
| Output-gap weight | 1.3 | 1.3 | 1.2 | 1.2 | 1.2 | 1.2 |
| Exchange-rate weight | 0.02 | 0.02 | 0.01 | 0.02 | 0.04 | 0.06 |
| Δ inflation standard deviation | 0.00 | 0.00 | 0.00 | 0.00 | −0.01 | −0.01 |
| Δ gap standard deviation | −0.01 | −0.01 | −0.01 | −0.01 | −0.02 | −0.06 |
Consider, first, the effect of including deviations of annual unit labour cost growth from 2½ per cent in an efficient Taylor rule. The reduction in inflation variability from responding to wages depends on how strongly policy is already reacting to inflation, with the response to wages becoming more muted, the more vigorous is the response to inflation. Wages depend on past inflation and the past output gap, so taking account of wages last period does little to reduce the variability in the system when the authorities are already moving the interest rate by a relatively large amount when inflation is away from target. Of course, if deviations of inflation from target elicit only a small policy reaction, better outcomes on inflation can be achieved by reacting more aggressively to deviations of unit labour cost growth from its target. Moreover, while the reaction coefficients on unit labour costs are relatively small on average, if the authorities can identify wages shocks then they are able to reduce inflation variability further by reacting more than the results above suggest.
Table 2 also includes the effect on the efficiency frontier of including the deviation of the real exchange rate from its equilibrium value in the reaction function. Since the exchange rate for the current period is known, the current, rather than lagged, value is included. Efficiency gains accrue to both inflation and output: when the exchange rate is above its equilibrium value it is both disinflationary and contractionary, and so responding to the exchange rate reduces the variability in both inflation and the output gap. The weight on the exchange-rate deviation increases as the weight on inflation increases, and the reduction in the variability in inflation and the output gap increases as the weight on the exchange rate increases. If the level of the real exchange rate is out of alignment with fundamentals, say by 10 per cent, this rule suggests that the appropriate policy response is to move short-term interest rates by up to about half a percentage point, depending on inflation preferences.[23]
6. Is a Forward-looking Rule Better?
The policy rules discussed above set the interest rate based on the most recent available information, which we assume to be the data from the previous quarter. Output data for a particular quarter, for example, are usually released two to three months after the quarter has passed. Output and inflation are relatively persistent, as the autocorrelations in Table 1 indicate, so the recent past contains considerable information about the near future. By reacting to the most recent values of inflation and output, therefore, policy-makers capture some of the future movement in these variables. But the issue is whether policy-makers can stabilise the cycle more if they explicitly exploit this information by reacting to forecasts of the target variables.[24] This is examined in this section.
The forecasts of inflation and output used in the reaction function for this exercise are model consistent: they are the future outcomes implied by the system described in Section 2.2 when shocks in the current and future periods are not known and when the nominal interest rate is unchanged from the period before the forecasts are made. In other words, they are no-policy-change forecasts. These forecasts are calculated for the current period and for the next six periods out. The current period is also a forecast since the outcomes – or, more specifically, the ‘shocks’ – have happened but are not yet known. Figure 7 shows the efficient frontiers of the Taylor rule for the base case (information at t-1) and some of the cases when values are predicted for the current and future periods.
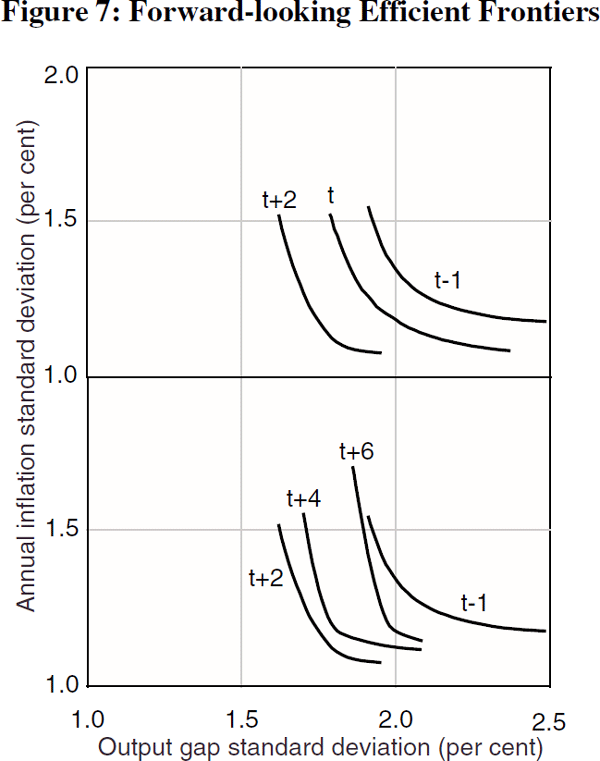
Clearly, model-consistent forecasts of inflation and output improve the efficiency of policy since the variability of inflation and output declines. As shown in panel 1, even using forecasts for the current period, rather than just using information at hand, yields significant gains. The gains are largest two periods out from the current period, after which, as shown in panel 2, they start to contract back to the base case. This pattern of rising then declining gains reflects two offsetting features in the analytical framework.
On the one hand, given that policy takes at least two quarters to have a direct effect on output in this framework, setting policy based on forecasts of the target variables two or more periods ahead automatically allows for a significant part of the lag process. This ensures that policy is moved earlier and so can better stabilise the economy. This explains why more of the gains from being forward-looking accrue to output than to inflation. It also implies that if the lag structure is in fact much shorter than that used here, so that policy has a more immediate direct impact on output, then the gains from being forward-looking are likely to be smaller.
On the other hand, the longer the forecast time horizon, the more likely it is that unexpected events will drive future values of inflation and output from the forecast values. If policy reacts to forecasts that are not realised, then variability in inflation and the output gap rises. Moreover, a key assumption in this exercise is that the forecast nominal cash rate is unchanged over the forecast period. As the forecast horizon is extended and inflation evolves, the real interest rate changes and starts to have an impact on the real economy. This tends to increase variability in the system over longer forecast horizons. This impact is avoided, however, when policy-makers set an optimal path for the interest rate based on all available information, along the lines outlined in Lowe and Ellis (1997); in calculating this optimal path, policy-makers need to look at the expected path of the economy over the indefinite future.
It is also apparent that the trade-off between inflation and output variability steepens with longer forecast horizons. Reducing inflation variability comes, for the most part, with a smaller cost to output variability. Again, this relates to the lags in the system. Over longer horizons, policy is able to take advantage firstly of the lags between rate changes and output, and then of the lags between domestic demand and inflation, to reduce inflation variability. Since it does not have to wait until inflation is already in the system, the output costs of reducing the variability of inflation pro-actively are lower than otherwise.
What is not apparent from Figure 7 is that the pattern of weights in the efficient frontier changes in two ways as policy becomes more forward-looking. In the first place, policy becomes more activist.[25] For example, the median weight on output, which is 1.1 for the baseline rule, rises to 1.3 when forecasts for the current period are used, and then to 2, which is the top of the range examined, when forecasts for two periods are used. Past values of inflation and output may be good predictors of future inflation and output, but they are still imperfect. If policy responds too vigorously to past information, it generates additional instability. But forecasts generated from the system are better predictors of future inflation and output than past inflation and output themselves, and so policy is more activist when it has better information. To use a well-worn metaphor, everyone would drive more slowly if all they saw was the road behind them, and not the road in front.
This high degree of policy activism, however, probably exaggerates what is achievable in practice. The forecasts are model consistent – policy-makers are assumed to know how the economy works, they just do not know the shocks, and so they cannot be systematically wrong. But the actual economy is dynamic and policy-makers only learn the structure of the economy with a lag. This may recommend caution. Indeed, if the economy is evolving and policy-makers only learn about this gradually, the weights in an efficient forward-looking Taylor rule are smaller than otherwise.[26]
Moreover, as Lowe and Ellis (1997) argue, policy change requires consensus, and it is much easier to persuade others with data than with someone's forecasts. The cold hard facts are more likely to generate consensus than an assertion about the outlook for the economy. Finally, greater activism implies that the nominal interest rate becomes more variable. For example, using weights which minimise the sum of inflation and output variability, the standard deviation of the quarterly change in the nominal interest rate is 1.1 per cent for the base rule but 2.4 per cent for the 2-period ahead forecast rule. This degree of variability is unprecedented, and may have other, deleterious, effects on the economy; see Lowe and Ellis (1997).
The second effect is that, for a given trade-off between the variability in inflation and the output gap, the relative weight on inflation increases as policy becomes more forward-looking. For example, the average ratio of the inflation weight to the output weight at points where the slope of the efficient frontier is 1, rises from about 0.6 for the backward rule to about 0.8 for the t+2 rule, and then to about 3 for the t+6 rule. The relative weight on the output gap is higher in a backward-looking rule since it helps predict future inflation. When the rule is forward-looking, however, the information about incipient inflation embodied in the output gap has already been exploited, and so the relative importance of the gap in further reducing the variability of inflation falls. Overall, the relative weight on inflation should increase as policy becomes more forward-looking.
7. Conclusion
This paper uses a data-consistent small open-economy model for Australia to assess the properties of various nominal interest-rate rules. We reach three main conclusions.
First, while no rule can eliminate all the variability in inflation and output, a rule is more efficient if it explicitly incorporates an inflation target. Efficient Taylor rules, which (like all Taylor rules) explicitly include the inflation target, reduce the variability in inflation and the output gap more than do price-level or nominal-income rules. This reduction is even larger if the inflation target is fully credible, with price and wage setters focusing on the central bank's inflation target, rather than recent inflation, in setting prices and wages. This suggests that an inflation target is also superior to a nominal-income target since it provides an identifiable anchor for inflation expectations.
Second, a feedback rule which pays considerable attention to the output gap substantially lowers the variability in inflation. Since inflation itself depends in part on the degree of excess demand, good policy focuses on the state of the business cycle in order to help stabilise inflation. Consequently, in a policy framework which is based on an inflation target, an efficient Taylor rule is preferred to a rule which only adjusts the nominal interest rate in response to deviations of inflation from target. But since inflation is also affected by factors other than excess demand, the nominal interest rate also has to respond to what is happening to inflation if the inflation target is to be met (and this response is relatively bigger, the more forward-looking policy becomes). Each efficient Taylor rule is distinguished primarily by the weight on inflation. Increasing this weight initially comes at a very low cost to greater output variability. But squeezing as much variability out of inflation as possible comes at the cost of considerably more variability in output.
Third, since the simple Taylor rule uses data from the previous quarter, any variable which provides information about inflation and output in current and future periods improves the efficiency of the rule. Efficiency can be modestly improved, for example, if policy-makers also take account of recent developments in wages and the real exchange rate. Interest-rate feedback rules can stabilise the economy much more, however, if they are forward-looking, rather than backward-looking, and so take some account of forecasts. Forward-looking policy is also more activist, and it reacts relatively more to inflation.
The numerical results in this paper are obviously model-dependent. A model with shorter lags, less persistence in prices, and a more detailed supply side may very well generate different results. As a consequence, the efficient rules and reaction coefficients discussed in this paper are largely illustrative. Nonetheless, the general conclusions that monetary policy should focus on an inflation objective, should take account of the output gap, and should be forward-looking all seem to capture critical elements of the monetary-policy framework currently used in many countries.
Appendix 1: A Framework for Analysis
Most equations are written in error-correction form to capture long-run tendencies and relationships between variables, as well as dynamics.[27] Parameters are generally estimated. The specifications of the equations, diagnostics and comments are given below. Numbers in parentheses ( ) are standard errors. Numbers in brackets [ ] are p-values. When lags of a variable enter an equation, the p-value for a joint test of their significance is given. All variables except interest rates are in log levels multiplied by 100. Equations are estimated using quarterly data from 1980:Q3 to 1996:Q3 unless otherwise noted. The analytical framework draws on a number of published Bank papers and the contribution of several Reserve Bank economists, especially David Gruen, Geoff Shuetrim and John Romalis.
Endogenous variables
Output

where y is non-farm output, y* is OECD output, tot is the terms of trade, rtwi is the real TWI, r is the real cash rate and fy is farm output. The coefficients on the lagged levels of the terms of trade and the real exchange rate are calibrated so that a 10 per cent rise in the terms of trade boosts output by 2.4 per cent and a 10 per cent appreciation of the real exchange rate reduces output by 2 per cent in the long run. The equation is based on Gruen and Shuetrim (1994) and Gruen, Romalis and Chandra (1997).
Prices

where p is the Treasury underlying CPI, ulc is a measure of underlying unit labour costs, ip is tariff-adjusted import prices and gap is actual less linear-trend output. The restriction that the coefficients on prices, unit labour costs and import prices sum to zero is imposed. The equation is based on de Brouwer and Ericsson (1995).
Unit Labour Costs

where egap is the output gap plus 1 per cent (which is an estimate of the output gap required to generate the disinflation that occurred over the sample period). The equation was estimated by generalised least squares to correct serial correlation, and with the restriction that the coefficients on lagged inflation sum to unity. The equation is based on de Brouwer (1994) and Cockerell and Russell (1995).
Real Exchange Rate

where dum is a dummy variable which takes a value of one for 1980:Q3 to 1984:Q4 inclusive and zero otherwise; and r* is the world real short interest rate. The equation is based on Gruen and Wilkinson (1991), Blundell-Wignall, Fahrer and Heath (1993) and Tarditi (1996).
Import Prices

where wpi is Australia's trading-partner weighted-average export prices and twi is the nominal TWI.
Exogenous variables
Farm output, foreign output and foreign export price are estimated as ‘trend-correction’ models by which growth in the variable is regressed against a constant and the deviation of the level from a linear trend. This implies that the exogenous variables are not random walks, but return to trend after a shock.[28]
Farm Output

where fytrend is the trend level of farm output.
Foreign Output

where y*trend is the trend level of OECD output, estimated from 1980:Q4 to 1996:Q3.
Foreign export price

where wpitrend is the trend of the Australian trading-partner weighted average of world export prices. The trend was estimated over 1980:Q3 to 1996:Q3, while Equation (A1.8) was estimated over 1981:Q2 to 1996:Q3.
Terms of Trade

Foreign real interest rate

Identities
Real Interest Rate

where i is the nominal cash rate.
Nominal Exchange Rate

where p* is the foreign price level, a trade-weighted average of foreign consumer price indices.
| Australian Data Data | Source |
|---|---|
| Non-farm gross domestic product (average) | ABS Cat. No. 5206.0, Table 48. |
| Farm gross domestic product (average) | ABS Cat. No. 5206.0, Table 48. |
| Australian terms of trade (goods and services) | ABS Cat. No. 5302.0, Table 9. |
| Underlying consumer price index | Treasury underlying CPI ABS Cat. No. 6401.0, Table 10. |
| Real TWI | RBA 22-country real export-weighted exchange rate. |
| Real cash rate | Official cash rate (RBA, Bulletin, Table F.1) less four-quarter-ended percentage change in the Treasury underlying CPI. |
| Unit labour costs | RBA underlying series. Total wage and non-wage labour costs divided by output. Wages are average weekly earnings (ABS Cat. No. 6302.0, Table 2) re-weighted using Labour Force Survey weights. Non-wage labour costs are calculated from ABS Cat. No. 5206.0, Table 36, and other sources. Output is given by trend non-farm GDP(A) ABS Cat. No. 5206.0, Table 47. Adjustments are made to these data series to give an underlying measure. |
| Import prices | This series has been constructed from merchandise imports data (ABS Cat. No. 5302.0, Tables 16 and 18). Total computer (ADP and ADP parts) import values are deducted from underlying (RBA definition) total import values to give computer-adjusted underlying import values. This is divided by the difference between underlying total import volumes and computer import volumes, to give an import implicit price deflator. |
| Tariff rate | Seasonally adjusted customs duty divided by seasonally adjusted underlying import values. Underlying import values are defined as for import prices, above. Customs duty is provided by the Treasury, Budget Revenue Section, and seasonally adjusted using X-11. |
| OECD gross domestic product | Datastream, OCDGDP..D |
| World real short interest rate | Real rates for the US, Japan and Germany are calculated by subtracting
the four-quarter-ended percentage change in the CPI from the discount
rate. The real rates are aggregated using a GDP share-weighted average. Discount rates: RBA Bulletin, Table F.11. CPI: RBA Bulletin, Table I.1. |
| World price of exports | This series has been constructed from quarterly export price indices for Australia's major trading partners where available on Datastream. These are aggregated using an export-share weighted arithmetic average. Up to 19 countries are included in the index. |
Appendix 2: Simulation Analysis
To assess the properties of the various rules, simulations were run for each rule and set of weights using the framework of equations described in Appendix 1. Starting in equilibrium, the system was run over 1,000 periods using normal random errors for each equation which embody the historical covariance of those errors. The methodology follows Byrant, Hooper and Mann (1993, pp. 240–241).
For all the equations excluding the import-price equation, a variance-covariance matrix of the residuals is generated from the variances of the equations and the correlation matrix of the historical residuals. The upper triangle of Table A2.1 shows the correlation coefficients, the main diagonal the variances of each of the series, and the lower triangle the covariances of the variables. The lower triangle of Table A2.1 is copied and transposed into the upper triangle to obtain the symmetric variance-covariance matrix, ∑. The variance-covariance matrix is transformed by a Choleski decomposition to yield two triangular matrices, P and P′, which multiply together to give the original matrix: ∑ = PP′. In each period a vector of random errors, et, is drawn from a distribution of a standard normal random variable with a mean of 0 and a variance of 1. To calibrate the shocks with the historical covariances, et is multiplied by the lower triangular P, giving a vector ut = Pet. The elements of ut are the shocks used in the simulations. The same shocks were used in all the simulations. The simulations are performed using GAUSS, and the seed for the random number generator for 1,000 shocks is 1.
| Farm output | Foreign output | Non-farm output | Unit labour costs | Prices | Terms of trade | Real exchange rate | World export prices | World real interest rate | |
|---|---|---|---|---|---|---|---|---|---|
| Farm output | 69.2451 | 0.1494 | 0.0810 | 0.0649 | −0.1442 | −0.1713 | 0.1993 | 0.0209 | −0.0824 |
| Foreign output | 0.4520 | 0.1322 | −0.1078 | −0.0329 | 0.1814 | 0.1677 | −0.0225 | −0.1627 | −0.1803 |
| Non-farm output | 0.4028 | −0.0234 | 0.3567 | 0.1134 | −0.0035 | −0.1389 | 0.0500 | 0.0324 | −0.1206 |
| Unit labour costs | 0.2499 | −0.0055 | 0.0313 | 0.2141 | −0.1177 | 0.1579 | 0.0084 | 0.1636 | −0.1487 |
| Prices | −0.2894 | 0.0159 | −0.0005 | −0.0131 | 0.0582 | −0.0791 | −0.1147 | −0.2011 | −0.0611 |
| Terms of trade | −2.4811 | 0.1062 | −0.1444 | 0.1272 | −0.0332 | 3.0292 | 0.1348 | 0.3592 | 0.1806 |
| Real exchange rate | 4.5409 | −0.0224 | 0.0817 | 0.0106 | −0.0758 | 0.6425 | 7.4982 | 0.1636 | −0.0311 |
| World export prices | 0.1831 | −0.0623 | 0.0204 | 0.0798 | −0.0511 | 0.6588 | 0.4720 | 1.1104 | 0.0494 |
| World real interest rate | −0.4368 | −0.0418 | −0.0459 | −0.0439 | −0.0094 | 0.2004 | −0.0543 | 0.0332 | 0.4063 |
For the purposes of the simulations, the constant terms in the equations in Appendix 1 are calibrated to place the system in equilibrium at the initial period. Also, the initial values for output, prices, unit labour costs, the exchange rate, farm output, import prices, the terms of trade are 100. The calibrated constant term for output is −3.80, for inflation is 0.53, for the real exchange rate is −1.55, for import prices is 11.21, for world output is 0.26, for the terms of trade is 13.46, for world prices is 0.26, and for farm output is 0.56.
Footnotes
We are indebted to our colleagues at the Reserve Bank, particularly David Gruen, Philip Lowe and John Romalis, for helpful comments and discussion. [*]
The literature on monetary-policy rules is enormous. Recent summaries are provided in McCallum (1990), Bryant, Hooper and Mann (1993), Hall and Mankiw (1994), Taylor (1996) and Bernanke and Mishkin (1997). [1]
Lowe and Ellis (1997) in fact report that the efficient Taylor rules perform well relative to the technically best outcomes. [2]
The equation for import prices in Australian dollar terms is not listed here since it simply estimates the dynamics of pass-through from world prices and the exchange rate. [3]
See McTaggart and Hall (1993), Gruen and Shuetrim (1994), de Roos and Russell (1996) and de Brouwer and Romalis (1996). [4]
Treasury (1993) finds that unit labour costs rise one-for-one with inflation but fall as the unemployment rate exceeds the NAIRU and as the unemployment rate rises. De Brouwer (1994) finds that wages rise with inflation and increased labour demand (proxied by the difference between output and consumer prices) but fall as inside unemployment rises. An Accord dummy was also significant and lowered wage growth over the 1980s. Cockerell and Russell (1995) present a similar equation for unit labour costs. [5]
Including the inflation rate means that the nominal-interest-rate rule is also a real-interest-rate rule, since the real interest rate is just the nominal rate less expected inflation, which is proxied by past inflation. [6]
It is, however, implicitly grounded on the real neutral interest rate since the nominal rate will only be constant when inflation is at target and output is at potential. Output is only stable at potential when the real interest rate is at its neutral value. [7]
See Debelle and Stevens (1995) and Grenville (1997a) for a discussion of this target. [8]
An alternative way to simulate the system would be to run it for each rule and set of weights over, say, 60 periods (15 years), and repeat the exercise many times with a new set of random errors. The method used is broadly equivalent to running the system over 60 periods with 15 different sets of random errors, but with the economy in equilibrium only at the start of the first run. It may be more realistic to evaluate rules from a point of initial disequilibrium than equilibrium. Moreover, the 1,000-period horizon has the advantage of showing the different long-run properties of particular variables, particularly of the price level and the nominal exchange rate, under different regimes. The trade-offs do not appear to be sensitive to the 1,000 shocks that were randomly drawn: we tried several different seeding values but found no substantive difference in trade-offs. We also ran a simulation using bootstrapping techniques – making a random draw with replacement of the actual residuals – for the Taylor rule and found similar results. In this case, the minimum standard deviations for inflation and the output gap were about 1.5 and 2.0 respectively, with the weights on inflation ranging from 0.5 to 1.7, and those on the output gap ranging from 0.8 to 1.3 (with a mean of 1 and median of 0.9). [9]
This criterion for efficiency indicates that the central bank cares about inflation and output separately, rather than their amalgam in the form of nominal income. One way to think about this is that if nominal income growth is 5½ per cent, for example, policy-makers at each and every period are not indifferent between growth of 5½ per cent with zero inflation and zero growth with 5½ per cent inflation. [10]
Annual, rather than quarterly, inflation is used since it is the focus of the Reserve Bank's inflation target. Moreover, annual inflation is less volatile than quarterly inflation since it averages out some of the noise in the quarterly series. Also, the ranking of the rules does not change if the outcomes are plotted in terms of the standard deviations of annual inflation and output growth. [11]
In the framework used here, unit labour costs respond to the output gap, and not also to output growth. If we include the change in the output gap in the unit labour cost equation, so that the speed with which the gap is closed also has a direct impact on inflation, then the Taylor rule still outperforms nominal-income rules. In this case, however, the Taylor rule should be augmented to include output growth, such that interest rates are higher the faster the output gap is closed after a recession. [12]
See, for example, Bryant, Hooper and Mann (1993). Henderson and McKibbin (1993) and Levin (1996) find that a Taylor rule with a large weight on output performs relatively well. Hall and Mankiw (1994) and Levin (1996), however, conclude that the Taylor rule dominates nominal-income rules. [13]
In a framework where interest rates change in response to actual values of particular target variables, the impact of an inflation shock on the path of inflation is smaller the more forward-looking are inflation expectations. In a rational-expectations model, for example, inflation expectations are tied to equilibrium inflation, which is the inflation target if policy is credible. Since the path of inflation, therefore, is less variable, interest rates and output are also less variable. This benefits the nominal-income-growth rule more than the Taylor rule, since, as explained in the text, nominal-income-growth rules respond to inflation plus the growth of output rather than inflation plus the output gap. Lower variability in inflation and output growth implies smaller oscillations, and hence a stronger policy response is less likely to make the system unstable. [14]
We do not show the outcomes which have a zero weight on inflation since the sample variance of inflation increases at rate t, and so approaches infinity as the sample size increases. [15]
The efficient weights for the nominal-income-growth rule range from 2.75 to 3.65 inclusive, with increments of 0.05. For the nominal-income-level rule, the range is from 1 to 1.5 inclusive, with increments of 0.1. The efficient weights on the inflation rule are from 0.5 to 1.1 inclusive, and for the price level are 0.001 to 0.003. The efficient frontier for the change rule has a constant weight on inflation of 0.005, while the weights on the output gap range from 0.065 to 0.08. [16]
The results that follow are robust to a series of significant changes to the structure of the model. For example, the efficient weights on inflation and output do not change when the covariances between the shocks of the equations are set to zero, so that only the variances matter. The weights are also similar when key relationships, such as the sacrifice ratio or the speed with which policy directly affects output, are changed. The sacrifice ratio, which is the amount of output that is given up to reduce inflation, is estimated over the past 15 years to be about 6, which is quite high (Stevens 1992). Reducing this to 2.5, however, hardly alters the weights on the efficient frontier; it only increases the variability in inflation since output shocks feed more quickly into wages and inflation. Similarly, reducing the lags from policy to output by one period hardly changes the weights on the efficient frontier. [17]
It should be noted that the real interest rate is occasionally negative. At point E, for example, with a neutral real rate of 3.5 per cent, the real interest rate is negative for 43 of the 1,000 periods, or about 4 per cent of the time (but the nominal interest rate is always positive). A low single-digit inflation rate target makes negative real interest rates much easier to achieve than an inflation target of zero. [18]
It may seem odd that as policy is more active in responding to inflation, the persistence of interest-rate changes increases, but the increased correlation in interest rates is caused by smaller negative correlations between inflation and output. [19]
Inflation will deviate from the target rate by −γ2/(1+γ1) times the difference between true potential output and the central bank's judgment about potential output. When the central bank responds relatively strongly to inflation, inflation will end up closer to the inflation target than otherwise. [20]
This also highlights the weakness of a constant real interest rate rule. If policy-makers want to set the real interest rate in a way which is consistent with output growing at potential, then they have no mechanism by which to judge whether the rate they choose is the right one or not. [21]
There are also other factors, like increasing international integration of goods markets, deregulation of labour markets and declining unionisation rates, which suggest that wages shocks in the future will be smaller or less frequent than in the past (Grenville 1997b). [22]
Reacting directly to the terms of trade, which is the key determinant of the real exchange rate, is never efficient. [23]
In a simple model where the policy instrument affects output with a lag and where output affects inflation with a lag, Svensson (1996) argues that it is optimal for policy-makers to set the nominal instrument using forecasts of inflation since this captures all relevant information. [24]
More activist policy is not the only, or main, reason why the variability of inflation and the output gap declines. If forecasts are fed into the rule with baseline weights, there is still a marked reduction in variability. [25]
We tested this by estimating a forward-looking model where the coefficients in the equations of the system evolve over time. Policy is less activist when policy-makers learn the true model with a lag than when they know how the system is evolving. [26]
Moreover, if there is non-stationarity in the data, as may be the case for output, prices, unit labour costs and possibly the real exchange rate, this representation is a way to deal with important statistical issues. [27]
While the debate on whether GDP follows a deterministic or stochastic trend is large, the tide seems to have turned in favour of deterministic trends (Diebold and Senhadji 1996). Whatever the case, our equation is diagnostically clean. What may be more controversial is the assumption that the foreign price level is trend stationary. This is unimportant since the exchange rate is floating, and so foreign nominal shocks have no effect on the domestic economy or inflation rate. [28]
References
Ball, L. (1997), ‘Efficient Rules for Monetary Policy’, NBER Working Paper No. 5952.
Bernanke, B.S. and F.S. Mishkin (1997), ‘Inflation Targeting: A New Framework for Monetary Policy?’, NBER Working Paper No. 5893.
Blundell-Wignall, A., J. Fahrer, and A. Heath (1993), in A. Blundell-Wignall (ed.), ‘Major Influences on the Australian Dollar Exchange Rate’, The Exchange Rate, International Trade and the Balance of Payments, Reserve Bank of Australia, Sydney, pp. 30–78.
Bryant, R.C., P. Hooper, and C.L. Mann (1993), ‘Design and Implementation of the Empirical Simulations’, in R.C. Bryant, P. Hooper and C.L. Mann (eds), Evaluating Policy Regimes, Brookings Institution, Washington, D.C., pp. 219–260.
Cockerell, L. and B. Russell (1995), ‘Australian Wage and Price Inflation’, Reserve Bank of Australia Research Discussion Paper No. 9509.
Debelle, G. and G.R. Stevens (1995), ‘Monetary Policy Goals for Inflation in Australia’, Reserve Bank of Australia Research Discussion Paper No. 9503.
de Brouwer, G.J. (1994), ‘Modelling and Forecasting Wages: First Steps’, Reserve Bank of Australia, mimeo.
de Brouwer, G.J. and N.R. Ericsson (1995), ‘Modelling Inflation in Australia’, Reserve Bank of Australia Research Discussion Paper No. 9510.
de Brouwer, G.J. and J. Romalis (1996), ‘External Influences on Output: An Industry Analysis’, Reserve Bank of Australia Research Discussion Paper No. 9612.
Department of Industrial Relations (1996), Review of Wage Trends, March.
de Roos, N. and B. Russell (1996), ‘Towards an Understanding of Australia's Co-Movement with Foreign Business Cycles’, Reserve Bank of Australia Research Discussion Paper No. 9607.
Diebold, F.X. and A.S. Senhadji (1996), ‘The Uncertain Unit Root in Real GNP: Comment’, American Economic Review, 86(5), pp. 1291–1298.
Edey, M. (1997), ‘The Debate on Alternatives for Monetary Policy in Australia’, paper presented at this conference.
Fuhrer, J. (1995), ‘The Persistence of Inflation and the Cost of Disinflation’, New England Economic Review, January/February, pp. 3–16.
Gagnon, J. (1997), ‘Inflation Regimes and Inflation Expectations’, Reserve Bank of Australia Research Discussion Paper No. 9701.
Grenville, S.A. (1995), ‘The Monetary Policy Transmission Process: What Do We Know? (And What Don't We Know?)’, Reserve Bank of Australia Bulletin, September, pp. 19–33.
Grenville, S.A. (1997a), ‘The Evolution of Monetary Policy: From Money Targets to Inflation Targets’, paper presented at this conference.
Grenville, S.A. (1997b), ‘The Death of Inflation?’, Reserve Bank of Australia Bulletin, May, pp. 34–41.
Gruen, D., J. Romalis, and N. Chandra (1997), ‘The Lags of Monetary Policy’, Reserve Bank of Australia Research Discussion Paper No. 9702.
Gruen, D. and G. Shuetrim (1994), ‘Internationalisation and the Macroeconomy’, in P. Lowe and J. Dwyer (eds), International Integration of the Australian Economy, Reserve Bank of Australia, Sydney, pp. 309–363.
Gruen, D. and J. Wilkinson (1991), ‘Australia's Real Exchange Rate – Is It Explained by the Terms of Trade or by Real Interest Differentials?’, Reserve Bank of Australia Research Discussion Paper No. 9108.
Hall, R.E. and N.G. Mankiw (1994), ‘Nominal Income Targeting’, in N.G. Mankiw (ed.), Monetary Policy, University of Chicago Press, Chicago, pp. 71–94.
Henderson, D. and W.J. McKibbin (1993), ‘A Comparison of Some Basic Monetary Policy Regimes for Open Economies: Implications of Different Degrees of Instrument Adjustment and Wage Persistence’, Carnegie-Rochester Conference Series on Public Policy, 39, pp. 221–318.
Levin, A. (1996), ‘A Comparison of Alternative Monetary Policy Rules in the Federal Reserve Board's Multi-County Model’, in The Determination of Long-Term Interest Rates and Exchange Rates and the Role of Expectations, Bank for International Settlements, Basle, pp. 340–366.
Lowe, P. and L. Ellis (1997), ‘The Smoothing of Official Interest Rates’, paper presented at this conference.
Lucas, R.E. (1976), ‘Econometric Policy Evaluations: A Critique’, in K. Brunner and A.H. Meltzer (eds), The Phillips Curve and Labour Markets, Amsterdam, North-Holland, pp. 19–46.
McCallum, B.T. (1990), ‘Targets, Indicators, and Instruments of Monetary Policy’, in W.S Haraf and P. Cagan (eds), Monetary Policy for a Changing Financial Environment, AEI Press, Washington, D.C., pp. 44–70.
McTaggart, D. and T. Hall (1993), ‘Unemployment: Macroeconomic Causes and Solutions? Or Are Inflation and the Current Account Constraints on Growth?’, Bond University Discussion Paper No. 39.
Quiggin, J. (1997), ‘The Welfare Effects of Alternative Choices of Instruments and Targets for Macroeconomic Stabilisation Policy’, paper presented at this conference.
Stevens, G.R. (1992), ‘Inflation and Disinflation in Australia: 1950–91’, in A. Blundell-Wignall (ed.), Inflation, Disinflation and Monetary Policy, Reserve Bank of Australia, Sydney, pp. 182–244.
Stuart, A. (1996), ‘Simple Monetary Policy Rules’, Bank of England Quarterly Bulletin, 36(3), pp. 281–287.
Svensson, L.E.O. (1996), Comment on J.B. Taylor, ‘How Should Monetary Policy Respond to Shocks While Maintaining Long-Run Price Stability?’, in Achieving Price Stability, Federal Reserve Bank of Kansas City, Kansas City, Missouri, pp. 209–219.
Tarditi, A. (1996), ‘Modelling the Australian Exchange Rate, Long Bond Yields and Inflationary Expectations’, Reserve Bank of Australia Research Discussion Paper No. 9608.
Taylor, J.B. (1993), ‘Discretion Versus Policy Rules in Practice’, Carnegie-Rochester Conference Series on Public Policy, 39, pp. 195–214
Taylor, J.B. (1996), ‘Policy Rules as a Means to a More Effective Monetary Policy’, Bank of Japan Monetary and Economic Studies, 14(1), pp. 28–39.
Treasury (1993), ‘Documentation of the Treasury Macroeconomic (TRYM) Model of the Australian Economy’, TRYM Paper, No. 2.