RBA Annual Conference – 1997 Designing Inflation Targets Andrew G. Haldane[*]
1. Introduction
This paper discusses some operational issues regarding the design of monetary frameworks in general and inflation targets in particular. Among inflation targeters,[1] these issues are well-known and manifold (see, inter alia, Yates (1995), McCallum (1995), Debelle (1997), Siklos (1997) and the country contributions in the volumes by Haldane (1995) and Leiderman and Svensson (1995)). They include:
- At what level to set an inflation target?
- Which price index to target?
- Over what horizon?
- Is a price-level or inflation target to be preferred?
- What is the optimal inflation-target bandwidth?
- Which shocks should be accommodated or exempted?
- Should inflation forecasts, and other internal information, be published?
- Should real, as well as nominal, magnitudes be targeted?
The maintained hypothesis running through this paper is that any discussion of these issues needs to be rooted in an understanding and quantification of two things: the underlying structure of the economy (‘technology’); and the welfare costs of inflation (‘tastes’). Of these, by far the least is known about the second. Yet it is difficult even to begin to address issues (a) – (h) without some notion of these welfare costs. The general point here is straightforward. Central banks target inflation because they think it costly. So it is only by knowing where the costs of inflation lie, and their size, that we can design monetary frameworks which ensure these inflationary costs are minimised.
In the inflation-targeting sphere, there are also any number of specific examples illustrating this general proposition. For example on issue (b) – the choice of price index – ‘underlying’ price indices may well do a better job of delineating trend inflation disturbances. But if the costs of inflation in fact derive precisely from deviations around trend inflation, then the usefulness of these underlying indices is much reduced. Likewise, the choice between an inflation and price-level target – issue (d) – has been shown empirically to hinge on a well-defined trade-off between high-frequency and low-frequency price-level variability (Duguay 1994). An inflation target delivers less of the former at the expense of more of the latter. But which of these variabilities – high versus low frequency – is the more damaging to welfare is an issue which can be resolved only by quantifying the costs of inflation. The same issue arises in the context of shock accommodation – issue (f). Conventional wisdom has it that equilibrium price-level shocks – for example, arising from supply shocks – ought to be accommodated or explicitly exempted. But such a choice stands or falls on how costly, in a welfare sense, we believe price-level disturbances to be.
Observing that the optimal design of an inflation target depends on the costs of inflation is, in principle, straightforward. But, in practice, economists have found measuring the costs of inflation an elusive task. The recent survey by Shiller (1996) on ‘Why Do People Dislike Inflation?’ is a telling diagnostic. While the survey found that the public were indeed strongly inflation averse, the primary reason for this aversion was inflation's perceived effect on real wages over time. That is not a welfare cost which monetary economists – with their predisposition towards dealing in deadweight-loss triangles – have much discussed.
Much has, of course, already been written on the theoretical foundations of the costs of inflation. Fischer and Modigliani (1975) is a classic treatment; see also Driffill, Mizon and Ulph (1990), Fischer (1981) and Briault (1995) for surveys. But there is much less work of an empirical nature quantifying these benefits and levelling likely costs against them. This paper could not hope to provide an all-embracing empirical account of the costs of inflation and their interaction with the design of inflation targets. So instead it focuses on just three of the operational questions raised at the outset: issue (a) – the optimal level of an inflation target; issue (c) – the horizon at which to target inflation; and issue (g) – the effects of greater central bank transparency. Sections 2–4 discuss each of these in turn.
In fact, resolving these three issues takes us a long way – perhaps all the way – towards specifying fully an optimal inflation-targeting framework. To see this, think of the generic form of the feedback rule under an inflation target,

where it is the policy instrument, πt+j is inflation at time t+j, Et is the expectations operator conditional on information at time t and earlier, π* is the inflation target, and γ is a positive feedback coefficient. Such a feedback rule encapsulates quite neatly the operational practice of most inflation targeters. A conditional inflation forecast serves as the intermediate or feedback variable. And the deviation between this feedback variable and the inflation target dictates the necessary degree of instrument adjustment. There is, in effect, inflation-forecast targeting (Haldane 1997; Svensson 1997).
But, as defined in Equation (1), the rule is not operational; it is underspecified in several important respects. First, there is a choice to be made about π* – the optimal level of the inflation target, issue (a). Second, there is the choice of an appropriate targeting horizon – the value of j in the feedback variable πt+j, issue (c).[2] And third, there is the whole question of what lies behind Et – which goes to the issue of the need for a degree of transparency to ensure the feedback rule, Equation (1), is verifiable and monitorable, issue (g).[3]
Each of these design issues is discussed here in turn. Each issue is shown to depend on both ‘taste’ and ‘technology’ parameters. And each raises some issues which, as yet, remain largely unresolved among macroeconomists. Below we try to summon together some of the evidence on these issues – both what we do know from existing research and, as important, what we might seek to understand from future research. Section 5 briefly concludes.
2. The Optimal Level of an Inflation Target
There are a number of issues which bear upon the question of the optimal level for an inflation target – the choice of π*. These are reviewed by, among others, Fischer (1994) and Yates (1995). Some of these issues are purely technical (‘technology’ issues); while others raise deeper-seated welfare-theoretic questions (‘taste’ issues). We discuss each in turn.
2.1 Measurement biases
Perhaps the major technical issue relates to measurement biases in published price indices. That measurement problem is endemic in monetary policy-making and is not at all specific to inflation targeting. After all, even the Bundesbank defines some medium-term inflation norm when formulating its monetary targets. Measurement bias is also an issue which has recently risen to prominence in policy circles following the report of the Boskin Commission (1996) in the United States. This concluded, among other things, that the bias in the US CPI was centred around 1.1 per cent per year.
Given the uncertainties attaching to bias estimates, a more meaningful metric of the likely measurement problem is provided by looking at ranges for bias – as do Crawford (1994) for Canada and Cunningham (1996) for the United Kingdom. Better still, we might calibrate the full probability distribution of likely measurement biases – as do Shapiro and Wilcox (1996) for the United States. Shapiro and Wilcox conclude that: ‘there is a 10 per cent chance that the bias [in the United States] is less than 0.6 per cent points and a 10 per cent chance that it is greater than 1.5 per cent points per year’. That conclusion accords, broadly speaking, with Canadian and United Kingdom evidence, where the ranges for bias lie at or slightly below 1 per cent point (Crawford 1994; Lebow, Roberts and Stockton 1992; Cunningham 1996).[4]
If we believe these estimates, then measurement problems with existing price indices are non-trivial but not enormous. But that still leaves unresolved a larger, and more important, conceptual question: whether existing price indices are meant simply to capture the acquisition cost of goods and services; or whether instead they are aiming to measure the cost of a constant-utility flow of services from these goods (a Hicksian price concept). The Boskin Commission called the latter a ‘cost of living’ index.
Existing statistical practice points firmly towards the former approach, despite the adjustments that statistical agencies routinely make for quality and new goods biases. The reasons for this are certainly pragmatic, for it is clear that the Hicksian price concept raises formidable statistical hurdles. To take a limiting example, consumption baskets now and in the last century are simply incomparable in utility terms given their radically different composition. It is difficult to think that any ‘new good’ or ‘quality’ bias adjustments could ever reconcile these two baskets. ‘Shall I compare thee to a bushel of wheat?’
Indeed, consumption-basket comparisons may be equally problematic over much shorter timeframes. For example, Shapiro and Wilcox (1996) give the example of cataract operations between 1969–93. On conventional measures, the price of these has risen tenfold over the period. But, hedonically adjusted, they find that the ‘true’ price has only risen by a factor of around three. Equally stark examples are provided by Nordhaus (1994) – in the context of the price of lighting – Cutler et al. (1996) – in the context of heart-attack treatment – and Hausman (1997) – using the example of cellular telephones.
But which of these price concepts is the one relevant to the policy-maker? Policy-makers are interested in price indices precisely because of the welfare losses induced by disturbances to this index. But to isolate these welfare effects, we need a measuring rod for prices which partials out utility changes induced from other sources – for example, those resulting from a changing composition or quality of the underlying consumption basket. That calls for a price index constructed along Hicksian lines, despite the practical difficulties this may raise. Indeed, this was precisely the conclusion of the Boskin Commission, which argued for the construction of a ‘cost of living’ index in the United States.
The above discussion highlights three points. First, some progress has recently been made towards quantifying CPI measurement biases. These are typically found to centre around 1 per cent per year – though there are considerable uncertainties either side of this mode, especially on the upside. Second, even these adjustments may well still leave us some way short of a price index suitable for policy analysis. Measurement biases cannot meaningfully be separated from behavioural considerations – the statistics from the economics. So, third, that calls for a closer interface between statisticians and economists if monetary policy is in future to be meaningfully calibrated.
It is telling that some of the early classic texts in monetary economics – for example, Fisher's (1911) The Purchasing Power of Money and Keynes' (1923) Tract on Monetary Reform – devoted at least one chapter to index-number theory and its application to price measurement. Such theory is rarely mentioned in modern monetary economics textbooks. The one area where index-number theory and micro-optimising behaviour has been extensively used is in the construction of Divisia monetary aggregates (Barnett 1980). Some of that same theory might usefully be applied in an inflation context.
2.2 Some cost-benefit calculus
The other factors affecting the optimal level for an inflation target relate more to (inflation) tastes than to (inflation) technology. As a practical matter, the trade-off here is between, on the one hand, the welfare costs of operating at an inflation rate different than the first-best, and, on the other, the disinflationary costs of moving to this first-best. The optimal level of an inflation target is given by the equation of these marginal costs and benefits. There are many such welfare costs and benefits. Here we review some of the more important of them.
But we first need a baseline rate of inflation around which to conduct this counterfactual experiment. Average inflation among the G7 is currently around 2–3 per cent. That is also in line with Australia's ‘thick point’ inflation target of 2–3 per cent (Debelle and Stevens 1995) and with the inflation targets set by most other countries, including the UK's 2.5 per cent point target. With measurement bias of around 1 per cent point, that leaves disinflation equal to around 2 per cent points to achieve price-stability – zero inflation – as commonly defined. This is the counterfactual question we pose: is it worthwhile lowering inflation targets by 2 per cent points?[5] We are ruling out the Friedman first-best – of deflation equal to the real rate of interest – on practical grounds. For no country is this a practical option at present.[6]
One general point is worth making on the costs and benefits of a 2 per cent point disinflationary transition. While disinflationary costs are commonly judged to be static (or transient), the benefits of lower inflation are likely to be dynamic (or permanent). The dynamic benefit is the permanent rise in the level or growth rate of GDP resulting from the move to a lower steady-state inflation rate (denoted B below, and expressed as a per cent of initial GDP). The static cost is the short-run output loss from disinflationary transition (denoted C below, again as a per cent of initial GDP), under the assumption of long-run monetary-policy neutrality. The optimal inflation rate is given by the equation of these marginal costs and benefits,

where r is the discount rate and g is the steady-state growth rate of the economy. The RHS of Equation (2) simply measures the discounted present value of the period-by-period welfare benefit from lower inflation. The welfare benefits of future generations are discounted at a rate r.[7] The growth term captures the fact that the GDP base on which the welfare benefits are calculated will grow over time (Feldstein 1979). As a back-of-the-envelope calculation, note that with r=5 per cent and g=2.5 per cent – plausible-enough estimates – even B=0.5 per cent of GDP will generate a steady-state welfare gain of 20 per cent of initial GDP. This is a huge sum.
Of course, there are considerable uncertainties surrounding such estimates. They are, for example, acutely sensitive to the choice of discount rate, about which it is difficult to make objective inferences. But 5 per cent is probably on the high side if we hold store by the existing microeconomic evidence. For example, we can back-out a discount rate from the representative consumer's utility function, by equating it with the marginal rate of substitution of consumption over time. Assuming CES preferences and an elasticity of marginal utility of 2, Feldstein (1995) arrives at a discount rate of 1.5 per cent in the US. By this metric, the present value of any positive B implies a potentially infinite welfare gain. But uncertainties also attach to B and C which might alter radically such simple calculus – and we now turn to those.
2.3 Measuring the costs of inflation
What existing empirical evidence is there on the costs of operating at 2 per cent inflation rather than price stability? Aggregate reduced-form evidence is instructive. A number of authors have looked at the potential effects of inflation on growth. But the evidence is decisively negative at the levels of inflation currently prevailing in developed countries. For example, in a cross-section study of over 100 countries, Barro (1995) finds little relationship between inflation and growth at rates of inflation below 10 per cent.[8] Likewise, Sarel (1996) finds no evidence of inflation inhibiting growth at rates of inflation below 8 per cent.[9] Taken together, there is little from this aggregate evidence to strongly support a move from single-digit inflation figures to price stability. Perhaps that is not altogether surprising, since theoretical models can yield conflicting conclusions regarding the effects of low and steady inflation on growth (Orphanides and Solow 1990).
But this evidence does not negate an effect of inflation on the level of GDP. In this respect, a number of recent studies have found encouraging results. Almost without exception, these studies have focused on the effects of fully anticipated inflation. Following Bailey (1956), this has the merit of allowing welfare experiments to be conducted: that is, Harberger deadweight-loss triangles are identified and quantified. For example, in a recent well-publicised paper, Feldstein (1996) calculates the benefits of a 2 per cent point disinflation in the US, operating through various tax-induced distortions to private-sector decision-making: to consumption behaviour; to residential investment; to money demand; and to debt servicing. He estimates this welfare benefit to be as much as 0.7 per cent of GDP in perpetuity in the US.[10]
Some equivalent studies have been conducted for Germany, Spain and the United Kingdom. These yield aggregate welfare benefits, when compared on a like-for-like basis, of around 0.85 per cent, 1.47 per cent and 0.21 per cent of GDP respectively. Table 1 provides a summary and decomposition of these results.
| US(a) | UK(b) | Germany(c) | Spain(d) | |
|---|---|---|---|---|
| Consumption(e) | 0.57 | 0.21 | 0.92 | 0.55 |
| Housing | 0.25 | 0.11 | 0.09 | 1.09 |
| Money demand | −0.03 | −0.02 | −0.04 | −0.07 |
| Debt servicing | −0.10 | −0.09 | −0.12 | −0.10 |
| Total | 0.68 | 0.21 | 0.85 | 1.47 |
|
Notes: (a) Taken from Feldstein (1996). (b) Taken from Bakhshi, Haldane and Hatch (1997). (c) Taken from Todter and Ziebarth (1997). (d) Taken from Dolado, Gonzalez-Paramo and Vinals (1997). (e) Assuming a zero-interest elasticity of saving. For Germany, where no zero-interest elasticity case is given, we have scaled down the estimates in line with Feldstein (1996). All of these benefits are calculated with a deadweight-loss parameter of around 0.4. |
||||
These estimates clearly vary quite widely, reflecting idiosyncrasies in national tax systems. Further, the implication of these studies is that the implied welfare gains could just as well (at least in principle) be brought about by adjusting tax policy, rather than monetary policy. But that said, all point to non-trivial GDP-equivalent welfare gains. With B lying between 0.2 and 1.5, then the present value of any welfare gain is between 10 per cent and 60 per cent of initial GDP, assuming r=5 per cent and g=2.5 per cent.
Feldstein's estimates look reasonably robust if we calibrate welfare benefits using a general, rather than partial, equilibrium model (Abel 1996). And recently there has been a number of other general equilibrium analyses of the welfare costs of inflation. These have tended to focus on the distorting effects of the inflation tax on money holdings. But they go beyond Bailey's (1956) original analysis to consider interactions with other private-sector decisions. Lucas (1995), for example, presents theoretical evidence to support a logarithmically specified money-demand function. This has the effect of raising greatly estimated ‘shoe leather’ welfare benefits – by Lucas' reckoning to as much as 1 per cent of GDP for a 10 per cent point disinflation.
Three factors call into question the plausibility of such an estimate. First, a very significant part of this welfare gain accrues not during the transition to price stability, but in the transition from price stability to the Friedman first-best of zero nominal interest rates. For example, based on a UK calibration over the period 1870–95, Chadha, Haldane and Janssen (1998) estimate that around three-quarters of the 1 per cent of GDP welfare gain comes when moving from zero to negative inflation rates. The same is true in the general-equilibrium analysis of Dotsey and Ireland (1996).[11]
Second, following from this, we have no empirically observed money-demand interest elasticities at rates of inflation at or below zero, so it is difficult to infer the form of the money-demand function around price stability. Mulligan and Sala-i-Martin (1996) attempt to obviate this problem by examining cross-sectional evidence on household money-demand functions. They infer, conversely, that money demand is actually rather interest-inelastic at low levels of nominal interest rates. The reason is that, at low interest rates, the small amount of interest income foregone reduces the incentive to substitute into interest-bearing alternative assets.
Finally, Lucas' (1995) estimates make no allowance for offsetting revenue effects (Phelps 1972). An interesting counterpoint is provided by two papers by Cooley and Hansen (1989, 1991). Both develop general-equilibrium models in an attempt to measure the welfare-distorting impact of the inflation tax. The earlier paper (Cooley and Hansen 1989) finds a significant distortionary impact. But once taxes are admitted (as in Cooley and Hansen 1991) this welfare gain is sacrificed entirely. Taken together, none of these general-equilibrium models would lead us to expect a significant additional welfare benefit arising from the inflation tax on money balances when moving from low positive inflation rates to price stability.
Some more recent studies have begun to quantify a wider set of welfare losses arising from the inflation tax than shoe-leather costs. For example, the Cooley and Hansen (1989, 1991) papers allow for explicit labour/leisure trade-offs, with lower inflation reducing the tax on consumption goods, and hence inducing increased labour supply and higher incomes. Further, because investment is deferred consumption, and because inflation acts as a tax on consumption, lower inflation also increases investment and the capital stock in this set-up. Dotsey and Ireland (1996) present a model in which lower inflation induces an employment redistribution away from (constant returns-to-scale) financial intermediation and towards (increasing returns-to-scale) production industries. So lower inflation, via an endogenous growth channel, can boost an economy's trend growth rate. This, in turn, has profound welfare implications. For example, in Dotsey and Ireland moving from price stability to the Friedman rule increases trend growth by as much as 0.2 per cent points, with a corresponding welfare gain of over 2 per cent points of GDP per year.[12]
In a similar spirit, English (1996) looks at the effects of inflation on financial-sector size in a cross-section of countries. He finds, on average, that each 10 per cent point rise in inflation raises the share of the financial sector in GDP by 1½ per cent. This is a direct measure of the resources lost as a result of inflation. But again such a finding, like those of Cooley and Hansen (1989) and Dotsey and Ireland (1996), would seem to be more relevant during the transition to low and stable inflation rates, than to when such rates have already been achieved. For example, English notes that the inflation/financial-sector-size relationship disappears once the six-highest inflation countries are removed from his panel. So while these studies highlight behaviourally important welfare costs, it is difficult to believe they would add more than a few basis points to our estimate of B.
All of the above studies, of course, aim to quantify the costs of a fully anticipated inflation. What of the likely costs of unanticipated inflation? There seems to be a relative dearth of empirical evidence on these costs – or at least evidence which is well grounded in welfare economics. But it is the logical next step when assessing the welfare costs of inflation, given policy-makers' concern with stable prices rather than low average inflation per se. It would also be consistent with the evidence we have from the general public. Shiller's (1996) survey suggests that the largest perceived costs of inflation derive from inflation's adverse effect on real wages – historically the result of inflation ‘surprises’ and uncertainties.
Some stylised facts on inflation uncertainties are, however, illuminating. Figure 1 plots the mean and standard deviation of inflation in around 60 low-to-moderate inflation countries, averaged over the period 1965–95. It fits a line of best fit through this mean/variability relationship. As numerous time-series studies have shown, the mean/variance inflation relationship is clearly positive, statistically significant and proximately one-for-one. To map reduced inflation variability into welfare, we might think of using the results of Judson and Orphanides (1996). They find a strong cross-country relationship between inflation variability and growth, distinct from any effect from the level of inflation on growth. What is particularly striking is that they find – unlike with the inflation-growth relationship – that this link exists even among low-inflation countries (those with inflation below 10 per cent per year.) For these low-inflation countries, Judson and Orphanides find that a halving of the volatility of inflation might raise growth by as much as one quarter of one percentage point.
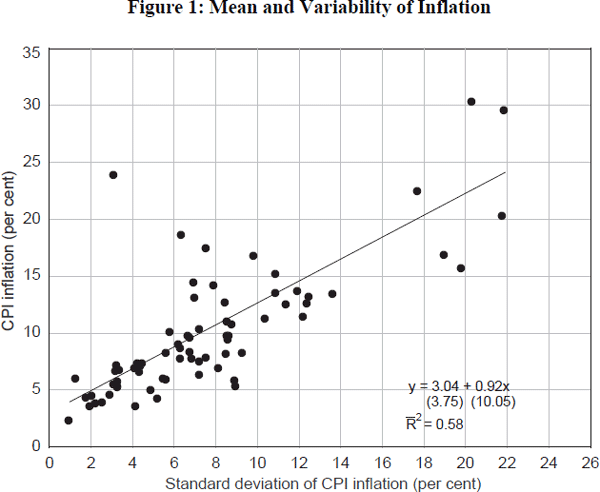
Given Figure 1, it is difficult to imagine that a halving of the volatility of inflation is feasible when moving from, say, 2–3 per cent inflation to price stability. There must, for example, be some minimum amount of inflation variability which is undiversifiable – and, indeed, desirable. But if the Judson/Orphanides ready-reckoners are even proximately correct, then reduced price variability could boost dramatically the welfare gains from a move to price stability. Even if lower inflation volatility has only a minuscule effect on growth, we would conclude that a move to price stability was unambiguously Pareto-improving – provided disinflation itself does not affect the economy's trend growth rate.
2.4 Measuring the costs of disinflation
These gross welfare benefits are only one side of the ledger. What of the costs? Almost all central bankers and most macroeconomists would believe such costs are transient; that the long-run Phillips curve is vertical. Taking money neutrality as read for the moment, we can infer disinflationary costs – the sacrifice ratio – either directly from a time-series estimated Phillips curve, or indirectly from an event study of disinflations (Ball 1994; Andersen 1992). Both, in their different ways, attempt to partial out supply shocks. And neither typically gives answers which are radically different. As a benchmark, we take Ball's (1994) average sacrifice-ratio estimates for Germany and the United States – the two countries whose past inflation performance has been closest to 2–3 per cent on average. This gives a sacrifice ratio of around 2–3 per cent: each percentage point of disinflation has, on average, been associated with a cumulative output loss (relative to trend) of around 2–3 per cent.
For plausible discount and growth rates, such transient losses (C) would almost certainly fail to counterbalance the permanent gains (B) outlined in the previous section. For example, the break-even welfare benefit necessary to counterbalance disinflationary costs of around 5 per cent points (2.5 per cent of output loss for each percentage point of inflation reduction) is around 0.125 per cent of GDP.[13] That is well below even the tax-induced welfare distortions outlined in Table 1 – before we even begin to consider the other welfare benefits of reducing anticipated and unanticipated inflation. So on the basis of this simple cost-benefit calculus, we would conclude that a shift to price stability – an inflation target of zero – was of clear net welfare benefit.
But uncertainties necessarily attach to estimates of disinflationary costs, C. Perhaps the biggest problem with existing sacrifice-ratio estimates is that they are drawn from prior – and therefore very different – monetary regimes. If expectational behaviour changes with regime, then so too will sacrifice-ratio estimates based around expectational Phillips curves. In particular, there are three reasons – in increasing order of potential importance – why historically estimated sacrifice ratios may understate the transitional output costs of disinflation.
2.4.1 Summers effects
This refers to the non-negativity constraint on nominal interest rates which, when zero inflation is targeted, in turn places a non-negativity constraint on real interest rates (Summers 1989). This constraint may then damp the ability of monetary policy to conduct effective stabilisation policy around price stability in the face of shocks, thereby raising output variability.
This Summers constraint will clearly bind more tightly, the closer is an inflation target to zero. But it is difficult to believe the cost would be punitive. Below-equilibrium (rather than negative) real interest rates ought to be sufficient to deliver output stabilisation in the face of the vast majority of shocks – the US experience in the early 1990s being perhaps a good example. And what little empirical work there is on this issue also finds this to be the case (Fuhrer and Madigan 1994).[14] Even in the face of large deflationary shocks, fiscal policy can always step into the breach – as has been the case recently in Japan.
2.4.2 Convex Phillips curves
A voluminous literature has recently emerged testing for Phillips-curve convexities – implying higher disinflationary output costs, the lower is inflation. These have been tested in many ways: using time series (inter alia, Clark, Laxton and Rose 1995; Laxton, Meredith and Rose 1995; Debelle and Laxton 1996); using cross-country data (Ball, Mankiw and Romer 1988); and using event studies (Ball 1994). Taken together, the evidence is broadly – though by no means overwhelmingly – supportive of some degree of Phillips-curve convexity in some countries.
One possible explanation of such convexities is downward nominal wage and price rigidities.[15] There are several strands of evidence here, summarised in Yates (1997). One has looked at the effects of inflation on the distribution of wages and prices. Under the null of downward rigidities, the skewness of the wage/price distribution ought to be decreasing in inflation. Aggregate wage and price data have generally rejected this null: for example, Lebow et al. (1992) in the US; Crawford and Dupasquier (1994) in Canada; Rae (1993) in New Zealand; and Hall and Yates (1997) in the UK. But disaggregated data for the US – Card and Hyslop (1996) and Groschen and Schweitzer (1997) – have been more supportive. Another strand of the literature has looked explicitly at the incidence of nominal wages cuts. Here the evidence is more conclusive. For example, Akerlof, Dickens and Perry (1996) argue that nominal wage cuts in the US are very rare, based on panel data and survey evidence. And the same seems to be true in the United Kingdom (Yates 1997).
But there are reasons why even these findings may not close the case on downward nominal rigidities. For example, because of trend productivity growth, real wage adjustment – and hence factor reallocation – can still be effectively brought about even without nominal wage cuts. And, perhaps most important, all of the above tests are subject to a significant Lucas critique: the absence of any data drawn from a regime approximating zero inflation.
Using pre–Second World War data, during which time the monetary regime better approximated price stability, takes us some way towards countering this critique. Figure 2 plots some Phillips curves for the United States (over the period 1800–1938) and the United Kingdom (over the period 1831–1938). GDP deflator inflation is plotted on the y axis; and a measure of the output gap on the x axis, with trend output estimated using a Hodrick-Prescott filter.[16] The data have been crudely purged of supply shocks by excluding observations where the change in the output gap and price level in any given year was of the opposite sign. A second-order polynomial line of best fit is fitted through the data.
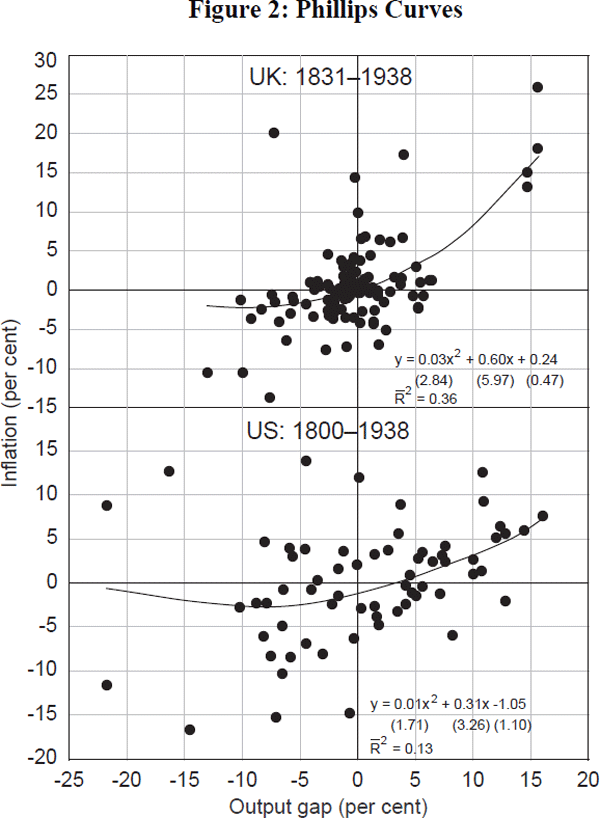
Two features are evident from Figure 2. First, the estimated Phillips curves are fairly flat when averaged around a regime approximating price stability. And second, more importantly, while there is evidence of some degree of convexity in these curves, it is still not that substantial. Although the output costs of disinflating increase as inflation falls, the increase is reasonably small. For example, the average implied sacrifice ratios for the UK and US from Figure 2 are between 1.5 and 3. This is not very different to the benchmark estimates used above. Such a conclusion is very much in keeping with the comments by Gordon (1996) on Akerlof et al. (1996), who refers back to the pre-Civil War period in the United States as an example of falling prices not being associated with subdued growth. So in sum, while Phillips-curve convexities might marginally increase disinflationary costs, this by itself still seems unlikely to offset the permanent welfare benefits outlined above. Our calculus so far would suggest that the optimal inflation target remains around zero.
2.4.3 Money non-neutralities
The third and far-and-away potentially the most important issue concerning possible understatement of existing sacrifice-ratio estimates is when there are significant hysteresis effects: if disinflation is capable of lowering on a permanent (or at least very persistent) basis the equilibrium level of GDP in the economy. That alters the cost-benefit calculus thus,

where D is the effect of a 1 per cent point disinflation on the natural level of output.
In general, empirical evidence on hysteresis effects is equivocal. But several recent papers have brought the issue into sharper focus. Ball (1996a) conducts a cross-section study of the effects of disinflation on the NAIRU in 20 OECD countries. Taking these estimates at face value, each percentage point of disinflation is associated with a 0.42 per cent point rise in the NAIRU; or, using an Okun coefficient of 2, with a 0.8 per cent fall in the level of output (D=0.8). That would almost certainly be enough to counterbalance the benefits of lower inflation outlined above.
The model presented in Akerlof et al. delivers an even higher hysteresis ready-reckoner for disinflations which are engineered close to price stability. Their simulations suggest that a move from 3 per cent inflation to price stability would raise the unemployment rate by around 2.1 per cent points – that is, 0.7 per cent points are added to the NAIRU for each percentage point of disinflation (an output loss of, say, 1.4 per cent). In the Akerlof et al. model, such hysteresis effects are particularly acute around price-stability because of nominal-wage rigidities. If such results were even moderately robust, then disinflationary costs would dwarf potential welfare gains.
So is there an empirical counterweight to these studies suggesting potentially significant monetary non-neutralities? Lucas' (1996) Nobel Lecture contained some stark cross-country evidence supporting long-run money neutrality. This drew on prior work by McCandless and Weber (1995), looking at average inflation and money growth rates – on an M2 definition – in 110 countries over a thirty-year period. On the basis of this, McCandless and Weber construct a figure which is virtually identical to the first panel in Figure 3. This uses similar data only for a smaller sample of around 80 countries.[17] A linear regression line is fitted through the scatter. The relationship is clearly positive and significant; in fact, it is insignificantly different from a 45° line.[18] Prima facie, this is strong evidence to support long-run money neutrality. Lucas observes: ‘The kind of monetary neutrality shown in this figure needs to be a central feature of any monetary or macroeconomic theory that claims empirical seriousness’. That might be construed as an effective refutation of the potential importance of hysteresis effects.
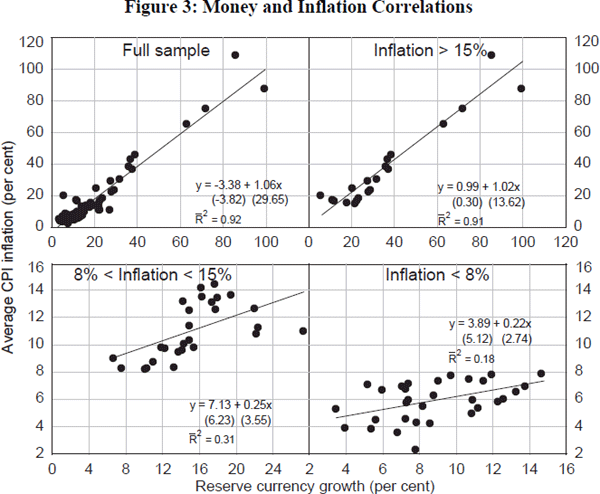
Or is it? The first panel of Figure 3 contains countries whose average inflation rates are much above the levels relevant to present-day inflation targeters. It is instructive, then, to stratify the sample by inflation regime. We employ a three-way split into ‘high’, ‘medium’ and ‘low’ average inflation countries. The ‘high’ countries are those with average inflation in excess of 15 per cent – for example, Venezuela and Paraguay in our sample. The ‘medium’ bloc is those countries where average inflation lies between 8 per cent and 15 per cent – such as India and Greece. And the ‘low’ countries are those with average inflation below 8 per cent – such as Australia and the United States. The split is somewhat arbitrary and means that even the low-inflation bloc has average inflation above the rates currently prevailing in the G7. But the decomposition gives us a broadly equal number of countries in each bloc and allows us to draw some illustrative conclusions.
The second, third and fourth panels of Figure 3 repeat the correlation analysis from the first panel for each of these three country blocs. For the high-inflation countries, the picture is virtually identical to that when using the full sample of countries. The regression coefficient is insignificantly different from one, offering strong support for money neutrality. But the pattern changes – to an ever-greater degree – when we look at the medium-and low-inflation countries. For example, from Figure 3, a 1 per cent point rise in average money growth in the low-inflation countries is associated with a rise in inflation of only around 0.2 per cent points.
How do we account for this apparent non-neutrality? From the quantity equation,

where π is inflation, m is money growth, v is velocity growth and y is
real output growth. So 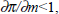 as was found empirically,
could plausibly be the result of the effect of average money growth on velocity
as was found empirically,
could plausibly be the result of the effect of average money growth on velocity
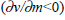 rather than on real output
rather than on real output 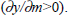 Observed correlations
refute that explanation. Figure 4 plots average money growth against average
real GDP growth for our full sample of countries and for the three inflation
blocs. Again, for the full sample – as in Lucas (1996) – and for
the high-inflation bloc, there is no statistically significant correlation
between average money growth and real growth. But that conclusion breaks down
for the medium-and low-inflation countries. For example, a 1 per cent point
rise in money growth among low-inflation countries is on average associated
with a 0.3 per cent rise in average real GDP growth.
Observed correlations
refute that explanation. Figure 4 plots average money growth against average
real GDP growth for our full sample of countries and for the three inflation
blocs. Again, for the full sample – as in Lucas (1996) – and for
the high-inflation bloc, there is no statistically significant correlation
between average money growth and real growth. But that conclusion breaks down
for the medium-and low-inflation countries. For example, a 1 per cent point
rise in money growth among low-inflation countries is on average associated
with a 0.3 per cent rise in average real GDP growth.
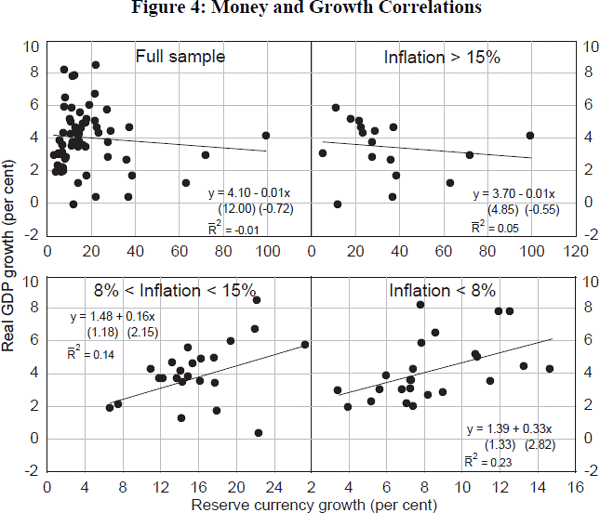
Of course, these are just time-averaged cross-country correlations. So we can infer little of a causal nature from them. One plausible explanation of these findings is, for example, that a third variable – financial development – is driving all the variables in the system. That would account for the simultaneous occurrence of low inflation (because of improved monetary and fiscal policy-setting), rising velocity (because of substitution into alternative near-money assets) and low growth (because of growth convergence). But another is that there are some monetary non-neutralities evident in economic systems as they approach low inflation rates. If the latter conclusion has any weight whatsoever – were lower inflation to reduce trend output growth – it would sweep away all of the welfare benefits of lower inflation highlighted earlier. It would justify sticking with inflation targets at around current levels. For that reason, it probably deserves further research.
3. The Choice of Targeting Horizon
3.1 Inflation-forecast targeting
At what horizon should inflation be targeted? From Equation (1), that is an issue which inflation-targeting countries cannot duck if they are to have a well-defined feedback variable, Etπt+j. The horizon problem raises two further, logically distinct, questions.
The first is the periodicity of inflation which the authorities should monitor and feedback from – for example, monthly, quarterly, annually, or perhaps longer horizons.[19] To date, few central banks have made much of this periodicity point, most preferring either to leave the inflation horizon opaque or simply to express the inflation rate as an annual change. But the issues it raises are rudimentary to the design of inflation targets. And, again, resolving the periodicity question cannot be easily detached from the welfare costs of inflation; it turns ultimately on whether it is high-or low-frequency inflationary disturbances which are the more welfare-depleting.
In fact, the self-same issues arise here as when dealing, inter alia, with CPI exemptions. For example, the typical kinds of exemption from CPI consumption baskets are volatile items – such as food and energy prices in Canada – and one-off price-level shifts associated with discernible supply shocks, such as ‘significant’ terms-of-trade changes in New Zealand. The macroeconomic reasons for these exclusions are well-known.
But what of the potential costs? For example, it could be that the very reason agents dislike inflation is because of volatility in the prices of everyday goods in the shops – food, utility prices etc. Were that the case, it would argue persuasively against their exclusion from targeted price indices. Further, there is support from Shiller's (1996) survey for the idea that agents would prefer a fixed price level, rather than inflation rate. When asked whether a price-level shift ought to be reversed, only 10 per cent of respondents in the US believed that it should not. Fascinatingly, virtually all economists, when asked this question, thought that price-level drift ought to be accommodated. Nowhere in Shiller's survey were the differences between the views of the general public and those of economists more acute. If we take the public's views seriously, then the choice of inflation periodicity or of CPI exemptions or of price-level versus inflation targets goes well beyond the narrowly technical – beyond even the macroeconomics textbook. It takes us right back, in fact, to the welfare costs of inflation.
The second – more operational – issue is just how forward-looking monetary policy needs in practice to be: what is the optimal targeting horizon j for the feedback variable in Equation (1)? The need for an explicitly forward-looking dimension to monetary policy is now widely accepted. Kohn (1995) of the Federal Reserve Board recently commented that ‘policy-makers cannot avoid looking into the future’. And even though such a forward-looking approach may only recently have found expression in the explicit design of monetary-policy frameworks, it has long been recognised by economists. In Keynes' (1923) Tract on Monetary Reform he observes: ‘…if we wait until a price movement is actually afoot before applying remedial measures, we may be too late’.
But what determines the optimal degree of policy forward-lookingness? This hinges, broadly speaking, on two factors: one ‘technology’ related – namely, the technical issue of the innate lags between the enactment of monetary-policy changes and their final effect on output and prices; and the other ‘taste’ related – namely, the relative weight the policy-maker places on output versus inflation variability. We consider these in turn.
3.2 The monetary-transmission lag
The lag between monetary-policy actions and their final effect on output and inflation has always been an area of considerable uncertainty. Following Friedman, these lags are not just ‘long’ but ‘variable’ too. But inflation-targeting central banks, operating according to (1), need necessarily to form a view of such lags. If it takes, say, one year before interest rates have any effect on inflation, then the central bank's inflation forecast needs to be formed at least one year ahead. In other words, the transmission lag places a strict lower bound on the optimal targeting horizon, j. This lower bound is dictated by simple technical feasibility. And it is clearly in central banks' interests to understand the limits of such a technical constraint.
There is a raft of empirical evidence addressing the transmission-lag question, much of it drawn from counterfactual VAR and macro-model simulations: for example, Sims (1994) for a selection of G7 countries. But the confidence intervals attaching to such simulations are known to be considerable. This raises two questions. First, does it much matter if we miscalculate the transmission lag when we set monetary policy? And second, what is the risk of such empirical mistakes occurring?
To gauge the potential effects of miscalculating the lag when setting monetary policy, consider a simple two-equation model of the economy,

and

where yt denotes real output, it the nominal interest rate, ut a white-noise inflation shock and ψ and β are positive coefficients. Equation (5) is an expectational Phillips curve. Equation (6) is an aggregate-demand relation. For simplicity and without loss of generality we: (a) define (5) and (6) as deviations from equilibrium – that is, we partial out the natural rate of output from the RHS of (5) and the LHS of (6), and specify no ‘core’ rate of inflation in (5); (b) consider only one shock – coming from the supply side, ut – but equally could have added aggregate-demand shocks to (6); and (c) normalise ψ to unity and omit any inflationary inertia in (5). So this is a standard aggregate-demand/aggregate-supply model. Note, crucially, that there is an explicit one-period lag in monetary transmission. Yesterday's output growth affects inflation today.[20]
First suppose that the monetary authorities estimate the lag correctly. Accordingly they follow the forward-looking inflation-target rule,[21]

where the inflation projection is formed one period ahead – the horizon at which monetary policy affects inflation. The solution for inflation is then,
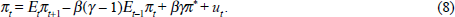
We solve this expectational difference equation using undetermined coefficients, by guessing a solution in the (minimum number of) predetermined state variables,

We can run the expectations operator through Equation (9) to give us expressions for Etπt+1 and Et−1πt, giving us a set of undetermined coefficient constraints for φ0, φ1 and φ2. For stability the key constraint is that associated with φ1,

This has two roots. Following McCallum (1983), we choose the root which rules out ‘bubble’ solutions – the value of Equation (10) for which φ1 = 0 whenever β = 0 – giving,

So provided appropriate restrictions are placed on the feedback coefficient (γ > 1), inflation will be stable and stationary (φ1 < 1).
Now suppose the authorities overestimate the lag, believing it to be two periods. The inflation-target rule is then

which can be solved in an exactly analogous way to give a stability condition,

This gives an identical stability restriction for inflation as in the case where the transmission lag is correctly inferred.
Finally, what if the transmission lag is underestimated by one period, giving a policy rule,

Solving as before, ruling out the ‘bubble’ root,

Equation (15) tells us that φ1 will be unambiguously negative and hence that inflation will be oscillatory. Underestimating the transmission lag will generate inflationary cycles – and the larger the feedback coefficient, γ, the larger the cycles. Indeed, at high values of γ, these oscillations could become explosive. So the message from these simple models is that underestimating the transmission lag is likely to have the more damaging impact on inflation control. It may lead to monetary policy generating cycles of its own. This really serves to underscore Kohn's comment – that monetary policy needs by necessity to have a forward-looking dimension if it is not itself to be a source of instability.
3.3 Some evidence on the lag
What evidence is there that such an underestimation of the transmission lag is likely? There are many reasons why we might be uncertain about the monetary-transmission lag. But perhaps the deepest-seated uncertainty is that existing evidence on transmission lags is drawn from the 1970s and 1980s – a very different, higher-inflation regime than the one operating today. Furthermore, there are theoretical grounds, and some anecdotal evidence, to suggest that the transmission lag is not invariant to such changes in inflation regime; it may well alter the lag.
Existing theory is ambiguous on the direction of this effect. On the one hand, low inflation might increase nominal rigidity in the economy and so lengthen (and deepen) the process by which monetary policy impacts on prices and output (Ball, Mankiw and Romer 1988). On the other, if lower inflation generates higher credibility, then expectational adjustment may well be quicker – and transmission lags will correspondingly be shorter. Anecdotal evidence, such as it is, seems to suggest the former effect may dominate. For example, a well-known stylised fact among high-or hyper-inflation countries is that transmission lags from money to prices are very short – often as little as months. And Friedman has commented that transmission lags were shorter in the 1970s than in preceding decades. If a low-inflation regime is likely to increase transmission lags, it increases the chances of underestimating the lag and hence disturbing inflation control.
Is there any formal evidence to support this anecdote? The time-series variation in inflation is, for most countries, insufficient to allow a meaningful comparison across different inflation regimes.[22] But cross-country variations in inflation are substantial enough to allow a comparison. Using the same set of countries as earlier – split into ‘high’, ‘medium’ and ‘low’ inflation blocs – Figure 5 plots the average correlation between short-term nominal interest rates and inflation in each of these country blocs at various leads and (in particular) lags measured in quarters.[23] The lead/lag is measured along the x axis, where a positive number indicates a relationship between lagged interest rates and inflation. The correlation coefficient is shown on the y axis. These correlations are averaged across each of the countries in each inflation bloc. Figure 5 also plots one standard-error bands around the mean, which are calculated as the cross-country standard deviation in the interest rate/inflation rate correlation at each lead/lag.
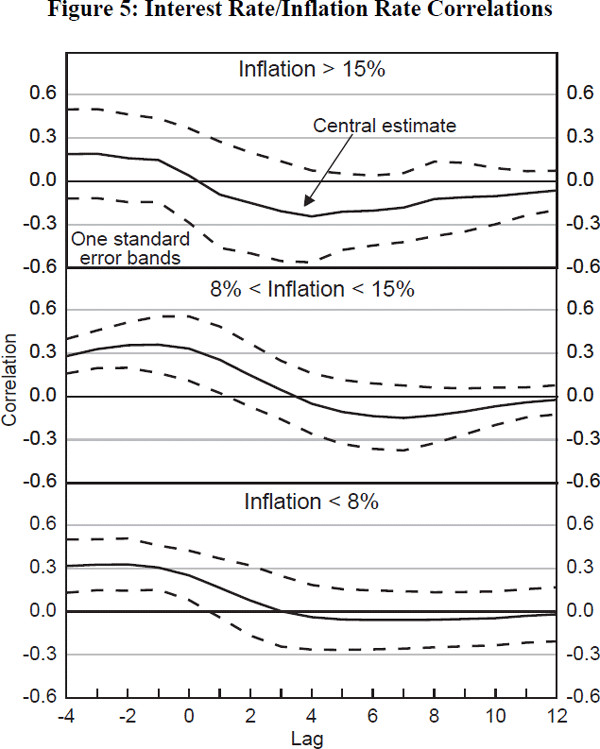
Several general features are evident from Figure 5:
- For each of the country blocs, the correlations generally indicate a negative relationship between inflation and lagged interest rates after a maximum of four quarters (and possibly sooner). This is as we would want if our correlations are to be interpreted as capturing the monetary-transmission lag, with higher interest rates depressing inflation over the short to medium run.
- The size and the timing of this negative relationship, however, varies quite markedly across inflation regimes. On size, interest rate/inflation rate correlations are much more negative for the high-than for the low-and medium-inflation bloc countries. For example, the average correlation between inflation and interest rates lagged one to two years is −0.2 for high-inflation countries; around −0.1 for moderate-inflation countries; and around −0.05 for low-inflation countries.
- That pattern is the mirror-image of the output response to an interest-rate rise in each of these countries (not shown in Figure 5). This is smallest for the high-inflation countries and becomes progressively larger as we move to the lower-inflation countries.
- On timing, the general pattern is that the inflation response takes longer, and is more protracted, the lower is the rate of inflation. For example, it takes only one quarter for the interest rate/inflation rate correlation to turn negative among the high-inflation bloc; and the largest negative correlation is found after around four quarters. For the moderate-inflation countries these lags are four quarters and seven quarters respectively; while for the low-inflation countries the lags are three quarters and eight quarters respectively.
We draw two conclusions from this. First, the observed responses in Figure 5 are consistent with a ‘nominal rigidity’ rather than a ‘credibility’ story. Monetary-policy changes appear to result, on average, in larger and more rapid responses from inflation, and more muted output effects, the higher is average inflation. Second, there is some evidence to support a lengthening transmission lag, the lower is average inflation. It could be that these effects are not sufficiently large to endanger monetary-policy setting. But without further data from a regime of price stability, caution is clearly appropriate.
3.4 Trading off output-inflation variability
Technical feasibility is one factor affecting the optimal targeting horizon, j. Another is the preferences of the authorities over output volatility on the one hand, and inflation variability on the other. This potential trade-off between output and inflation variability really goes to the heart of how best to conduct efficient stabilisation policy in the face of shocks. To see this, suppose there is an adverse supply shock, which pushes inflation above target and output below trend. How quickly the authorities then aim to return inflation to target – the choice of horizon for the feedback variable in Equation (1) – hinges on a trade-off. Faster disinflation – a shorter targeting horizon – reduces welfare losses deriving from inflation deviations from target. But it comes at the expense of a greater destabilisation of output in the short run. The obverse is true for slower disinflations. So the choice of targeting horizon (or speed of disinflation) can be thought of as an implicit trade-off between output and inflation variability.
These types of trade-off in the second moment of output and inflation have been popularised by the work of Taylor (1993). And the trade-offs themselves have been verified empirically using model simulations (Haldane and Salmon (1995) for the UK and Debelle and Stevens (1995) for Australia). What these studies typically find is evidence of a fairly malign trade-off, with very short or very long targeting horizons delivering extremely adverse output and inflation variability respectively. Such a trade-off is illustrated by the curve AA in Diagram 1.[24] Moving up the curve AA is equivalent to lengthening the implicit targeting horizon (reducing the speed of disinflation following a shock), thereby lowering output variability.
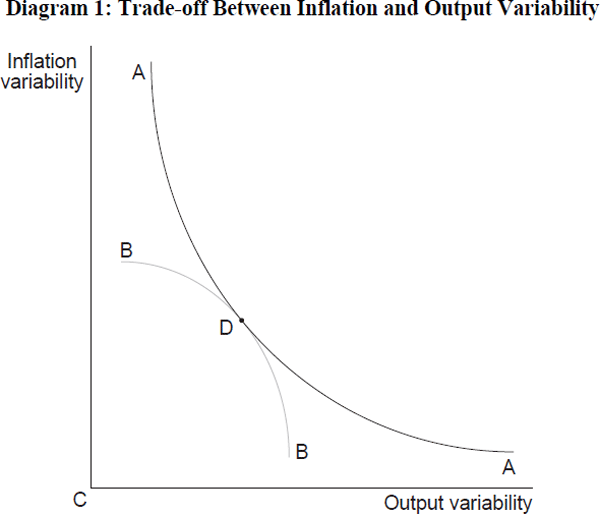
The trade-off curve can be thought to provide a menu of output/inflation variability choices for the authorities. But to locate the optimal targeting horizon we need also to define the preferences of the authorities over output/inflation variability. These are shown as the indifference curve BB in Diagram 1. The bliss point is clearly C, where output/inflation variability is minimised. This point is technically infeasible because it lies off AA. The optimal targeting horizon is given by the point D, where preferences are at a tangent to the technical constraint.[25]
From this it is clear that the optimal targeting horizon depends crucially on the marginal rate of substitution between output and inflation variability in the authorities' loss function. We would again expect such preferences to be rooted in an understanding of the relative costs of these two ‘bads’. The difficulty here is the relative dearth of welfare-theoretic analysis which allows us to weight output and inflation variabilities. Here is another area where there is scope for further research.
No inflation-targeting country has yet sought to make entirely clear, much less write into legislation, an explicit targeting horizon for their monetary framework. In many ways this is understandable. When inflation targets were first introduced, the low accrued stock of credibility among those central banks concerned meant that the first priority was to provide an anchor for inflation over the medium term. But now that inflation expectations have been more securely anchored, the next step in designing inflation targets is to think further about specifiying the transition path back to equilibrium following shocks. This is equivalent to specifying a targeting horizon – which brings with it all the issues and imponderables raised above.
Could such a choice of targeting horizon be left to the discretion of the central bank? Doing so endows the central bank with a degree of goal independence over the desired mix of output and inflation variabilities. In other areas – for example, in the specification of the inflation target itself – such goal independence is generally deemed undesirable. Those ‘taste’ choices are believed best left to government, who in turn are meant to reflect the preferences of the public themselves. If this argument is accepted, then it applies as much to the choice of inflation-targeting horizon as it does to the choice of inflation target itself.
4. Inflation Targeting and Transparency
4.1 Transparency in practice
A striking feature among central banks over recent years, in particular among inflation-targeting central banks, has been the extent to which they have sought to reveal more of their monetary-policy hand. There has been a quantum leap in the degree of transparency in central banks' actions and intentions. Among inflation targeters, this is arguably the feature differentiating their prior and present monetary frameworks.
There have been a number of vehicles for this greater transparency. Perhaps the most important has been the publication of inflation and monetary-policy reports. These are now published in Canada, Spain, Sweden, New Zealand, the United Kingdom and Norway, even though the last of these countries does not have a formal inflation target as such. Among those inflation targeters without formal inflation reports, such as Australia and Finland, greatly increased efforts have been made to communicate and explain monetary-policy actions: for example, through press releases at the time of monetary-policy changes; or through forward-looking synopses of inflation prospects in regular central bank bulletins and speeches. Other such moves towards greater transparency and accountability include: regular appearances before parliamentary committees (Australia, Sweden, Spain and New Zealand, among others); published minutes of monetary policy council meetings (the UK); and published forecasts for inflation (the UK) and sometimes other variables too (New Zealand).[26]
The reasons for this greater transparency among inflation targeters are clear when we think about the feedback rule, Equation (1). The intermediate variable, from which the authorities feed back when setting policy, is the conditional expectation on the part of the authorities of the future path of inflation, Etπt+j.[27] But without a vehicle for communicating the central bank's intentions, such conditional expectations are clearly unobservable. Indeed, they can be accurately inferred only with knowledge of the entire conditional probability distribution of likely inflation outturns on the part of the authorities.
Given this, if the reaction function of the authorities, Equation (1), is to be monitored by the public, inflation-targeting central banks need to make transparent just what Etπt+j is and how it is being calculated. This could in principle be done qualitatively. But ‘words’ are likely to prove too opaque to be easily monitorable when describing a complete probability density function. So a preferred option is simply to publish the inflation forecasts which constitute the feedback variable. That is the approach taken by New Zealand and the UK. It allows the public to monitor the authorities' feedback rule in operation (Svensson 1996). And it ought in turn to be credibility enhancing, as well as serving as a public-accountability device.
Indeed, given that an inflation forecast is really a summary statistic for myriad information variables, there may well be a case for publishing not only the inflation forecast itself, but details of the way it is compiled too: for example, the underlying model (or models) on which it is based; the exogenous-variable assumptions; residual or judgmental adjustments etc. That would allow outsiders to audit the forecast and verify its objectivity. In fact, only New Zealand comes even close to such a set-up.
The Bank of England does publish details of its conditional probability distribution for future inflation. This permits an explicitly probabilistic approach to the setting of monetary policy. For example, monetary policy in the UK has recently been set with a view to securing a ‘better-than-evens’ chance of hitting the inflation target. Interest rates have been adjusted such that more than 50 per cent of the conditional probability mass for future inflation lies below 2.5 per cent. The basis for that probabilistic, ‘better-than-evens’ approach has been the Bank's probability distribution for inflation. This probabilistic approach can be verified and monitored by the general public using the Bank's published probability density function.
What might be the obstacles to greater transparency, in particular about Etπt+j? One argument which has been put forward is that central bank independence makes an inflation forecast redundant, because it becomes very difficult then to publish an inflation forecast different than the target. But that is a non-sequitur. An independent central bank can always solve the dual of the inflation-control problem and trace out instead a profile for interest rates consistent with meeting their inflation target.[28] That is pretty much what the Bank of Canada does internally, backing out an implied path for monetary conditions which is consistent with their target.
Further, there may well be legitimate policy reasons for bringing inflation forecasts in line with the inflation target at different speeds over different horizons at different times. Some of the reasons for this were discussed earlier. The optimal targeting horizon depends on the size and incidence of shocks and on the authorities' preferences over output and inflation variability. Publishing an inflation forecast can serve as a signalling device about the nature of shocks and the authorities' response to them. In this case, publication is not only feasible but positively desirable as a way of clarifying the authorities' reaction function.
A second potential objection to publication might arise when the policy-making structure is explicitly federal – as with the Federal Open Market Committee (FOMC) in the United States. For example, in the US, inflation forecasts are put before the FOMC through the Fed Board's ‘Greenbook’. But these forecasts are explicitly staff projections; they do not necessarily constitute the views of any of the committee, not even the Chairman. Because of this, the ‘Greenbook’ projections are not published, except with the usual five-year lag. There is no published ‘FOMC’ forecast either, presumably because of the difficulty in finding consensus across the committee on how this ought to look.
But neither of these obstacles seems insurmountable. At the end of the day, the FOMC sets only one interest rate and so must implicitly have only one view – albeit a weighted-average view. That weighted-average view must in turn equate with some conditional forecast for inflation and possibly for other variables too. It is unclear what merit there is in leaving these forecasts implicit. Alternatively – and less dramatically – the Fed Board staff forecasts in the ‘Greenbook’ could be published with a less than five-year lag. As Romer and Romer (1996) have recently shown, these ‘Greenbook’ forecasts – for inflation, output etc. – have easily outperformed consensus outside forecasts in the recent past. So releasing this internal information would presumably reduce uncertainties regarding inflation and other variables of macroeconomic interest among the general public. It would also potentially help outsiders better understand the actions and intentions of the Fed itself, to the extent that ‘Greenbook’ information is used by the FOMC in its policy deliberations.
4.2 Transparency in theory
All of the above arguments are based on the assertion that greater central bank transparency is, on the whole, net beneficial. Does the existing academic literature provide support for this assertion? At least two literatures address this question: the time-consistency literature and the central bank secrecy literature.[29]
4.2.1 Time consistency and transparency
The time-consistency literature is well-known. Discretion imparts the incentive to generate inflation surprises for short-term output gain – an incentive which, under rational expectations, imbues the economy with an inflation bias (Barro and Gordon 1983). There is a variety of institutional means of circumscribing discretion and hence curtailing inflation bias. Two that are well known are the appointment of independent or ‘conservative’ central bankers (Rogoff 1985) and the adoption of (linear) inflation contracts (Walsh 1995a; Persson and Tabellini 1993). Both of these game-theoretic institutional fixes are believed by some to have analogues in the real world. The Bundesbank is, for many, the archetypal ‘conservative’ central bank; while New Zealand's Policy Targets Agreement is often thought to have parallels with a Walsh contract (Walsh 1995b).[30]
A third such institutional fix is greater transparency. Under a transparent monetary regime, inflationary opportunism would be quickly spotted and may not then even deliver a short-run boost to output.[31] This then decreases the incentive to generate an inflation surprise in the first place. The logic here is really the flipside of Cukierman and Meltzer (1986). In that paper, the central bank seeks ambiguity so that it can disguise inflation surprises. These days, inflation-targeting central banks are deliberately forgoing one means of camouflaging these surprises. This then serves as a public demonstration of their unwillingness to countenance such surprises – hence lowering inflation bias.
This notion can be formalised by returning to the inflation-targeting reaction function, Equation (1). Without information on Etπt+j, agents cannot infer whether the change in the policy instrument derives from news about the feedback variable (Etπt+j) or from a shift in the inflation target itself (π*). That uncertainty will lead risk-averse wage-bargainers to take out inflation insurance by raising their inflation expectations. Revealing Etπt+j simplifies the signal extraction problem, inducing wage-bargainers to take out less inflation insurance when forming their expectations – hence imposing less of an inflation bias.
4.2.2 The term structure and transparency
A second literature has emerged looking explicitly at the effects of central bank secrecy on financial-market behaviour. Its genesis was a legal enquiry in the US into the Fed's need for secrecy (Goodfriend 1986). The Fed defended its private information on the grounds that this helped stabilise short-term interest rates. And subsequently a series of papers have emerged analysing the theoretical basis of the Fed's defence (Dotsey 1987; Rudin 1988; Tabellini 1987).
The effects of transparency on conditional interest-rate variability seem reasonably clear. Transparency serves to reduce uncertainty – interest-rate forecasting errors – because forecasts are based on a superior information set. That is easily seen from Equation (1). The less the public know about the authorities' conditional expectations of future inflation, the less they know about the authorities' feedback variable. Hence, the larger are the interest-rate forecasting errors the public will make when guessing the authorities' policy actions.
The effects of transparency on unconditional interest-rate variability are less certain. But Dotsey (1987) and Rudin (1988) argue that transparency should increase unconditional interest-rate variability, for conventional LeRoy and Porter (1981) type reasons: the cleaner and more frequent the signal, the greater the responsiveness of asset prices to ‘news’.[32] These predictions ought to be empirically testable. And while the discussion in the literature to date has been couched in terms of short-term – in the US, federal funds rate – variability, the same arguments in fact apply along the whole of the yield curve. Transparency reveals information on the future, as well as current, behaviour of the monetary authorities; it hence affects expectations of future as well as current short-term interest rates.[33]
4.3 Some evidence on transparency
So what empirical evidence is there on the effects of transparency? To date, the empirical literature is sparse to non-existent on this issue. Below we offer some illustrative evidence, separated – again somewhat artificially – along the lines of the two literatures discussed above.
4.3.1 Inflation bias and transparency
Taking the time-consistency literature first, the testable implication here is that expected, and hence actual, average inflation should be lower the greater is transparency. But inflation targets have been in place for too short a time to allow any meaningful inference from actual inflation: the average duration of inflation targets is around 3–4 years, while the average transmission lag is itself around 2–3 years. It is for these reasons that Almeida and Goodhart (1996) conclude that the case for inflation targets is as yet ‘unproven’.
Alternatively, we might look directly at expected inflation. A number of recent papers have done so, typically using either bond yields (Freeman and Willis 1995) or surveyed inflation expectations (Almeida and Goodhart 1996; Siklos 1997) as a metric. Neither measure strongly supports the hypothesis that inflation expectations have fallen. But then neither measure is ideally suited to the task.
Surveyed inflation expectations typically refer to horizons (at most) one to two years ahead. But because inflation at those horizons is critically affected by the cycle, these expectations tell us more about the relative cyclical positions of economies than about the longer-term credibility of their monetary policies. And it is the latter hypothesis which is at issue in the time-consistency literature.
Bond yields do embody longer-horizon expectations. But even they need to be interpreted carefully. For example, Table 2 compares bond yield differentials between the inflation-targeting countries and an (equally weighted) average of the US and Germany on two dates: at the time these countries first announced an inflation target and currently. Table 2 clearly suggests some narrowing of yield differentials between the inflation targeters and the US and Germany. That is consistent with some credibility bonus. But the pattern is fairly disparate, with the Finnish differential falling by almost 400 basis points and the UK by only 100 basis points.
| Canada | Australia | Finland | Sweden | NZ | UK | Spain | |
|---|---|---|---|---|---|---|---|
| Regime begins | 1.69 | 1.35 | 3.74 | 3.66 | 3.43 | 2.22 | 3.19 |
| Currently | 0.30 | −0.50 | −0.10 | 0.92 | 1.60 | 1.22 | 0.84 |
| Change | 1.39 | 1.85 | 3.84 | 2.74 | 1.83 | 1.00 | 2.35 |
| Note: Differentials are with an equally weighted average of the US and Germany. Data are long-term – mostly 10-year – government bond yields. The dates on which the regimes start are: New Zealand, March 1990; Canada, February 1991; the UK, October 1992; Sweden, February 1993; Finland, March 1993; Australia, (around) April 1993; Spain, November 1994. | |||||||
There are two reasons why bond yield data might give a misleading impression of relative credibility gains. First, the data make no attempt to control for real interest-rate shifts. Second, and more important, bond yields are averages of future short-term rates and as a result are also cyclically sensitive. A less contaminated view of inflation expectations, abstracting from the cycle, is given by forward rates – point rather than average expectations. In particular, long-maturity forward rates can be used to abstract from the cycle and provide information on shifts in the perceived credibility of monetary policy.
Figure 6 attempts to control for the above two effects using UK data. The first panel looks at the forward-rate differential between the UK and Germany on three dates: just prior to the introduction of the UK's inflation target; just prior to the announcement of Bank of England operational independence; and currently.[34] From this, it is clear that the small fall in bond yield differentials in Table 2 obscures an interesting forward-rate pattern, with short-term forward rates diverging – because of divergent UK-German cycles – but longer-term forward rates converging markedly. As a result, in April this year the forward-rate differential between the UK and Germany was less than one percentage point from around 2002 onwards. And since the announcement of operational independence for the Bank, the differential has shifted down further to around zero from 2002 onwards. Since it is these cycle-invariant long-maturity forward rates that are the true arbiter of the perceived credibility of the new regime, the clear implication is that the UK's relative credibility has improved since the introduction of its inflation target; inflation bias has been reduced. This message is obscured looking just at bond yield data.
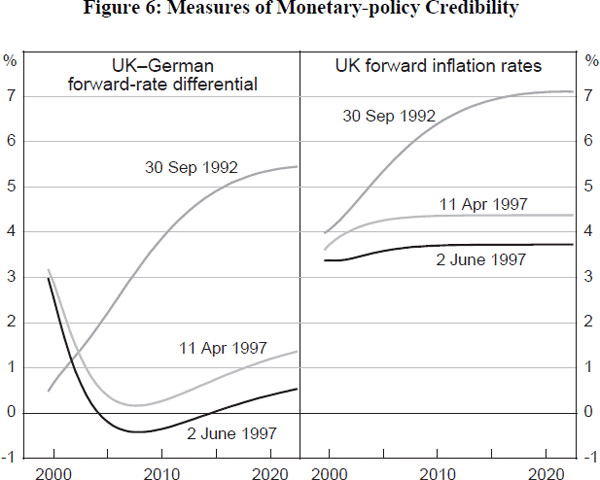
What of absolute credibility? The second panel of Figure 6 uses data from the UK's indexed-bond market to infer forward inflation expectations from the difference between the nominal and real forward-rate curves (Deacon and Derry 1994). It too suggests reduced inflation bias. For example, UK forward inflation rates expected in 2010 fell by almost three percentage points – from above 7 per cent to below 4½ per cent – between September 1992 and April 1997. And the announcement of Bank of England independence led to a further 50 basis-point drop in expected inflation, to a level of around 3.75 per cent. That compares with implied inflation expectations of over 7 per cent as recently as five years ago. If we make some allowance for inflation risk premia, then implied forward inflation expectations are now probably not very much above the UK's 2.5 per cent inflation target. So the message is clearly that absolute and relative inflation biases have fallen in the UK since the introduction of its inflation target. There is a variety of reasons why this might be the case. But greater transparency must be prominent among them, especially during the pre-independence period. It would be interesting to apply such forward-rate analysis to other inflation-target countries which have undergone transparency transformations.
4.3.2 The term structure and transparency
A more direct test of the effects of transparency is found by looking at interest-rate variability. We look at both short-and long-term interest-rate variability, recognising the effects of transparency on both. And in line with the literature, we draw a distinction between conditional and unconditional effects along the yield curve. Although the analysis again confines itself to the UK, the same technology could be applied elsewhere.
The effects of transparency on unconditional interest-rate variability are well illustrated by event studies around the time of ‘news’ releases. The two transparency events we focus on in the UK are the publication of the monthly minutes of the meetings between the Chancellor and the Governor,[35] and the publication of the Bank of England's Inflation Report – neither of which existed prior to the introduction of the UK's inflation target. The former release takes place on a monthly cycle; the latter on a quarterly cycle.
The top two panels of Figure 7 show the intra-day response of short-term interest-rate expectations derived from the futures market on the day of the transparency event; while the bottom two panels do the same looking at long-term interest-rate expectations in the futures market. All of these responses are averaged across the events in question: the thirty-six Chancellor/Governor minutes releases between April 1994 and March 1997; and the seventeen Inflation Report releases between March 1993 and March 1997. The time of publication is also shown on the figures.
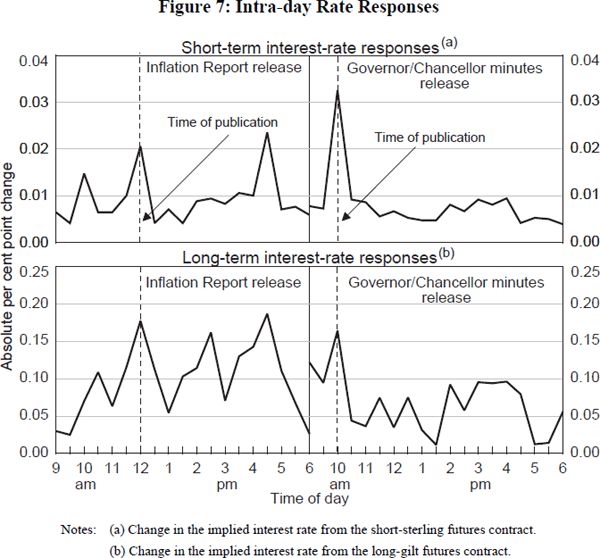
It is clear from both panels that these transparency events have clear effects on both short-and longer-term interest-rate expectations. As might be expected, these effects are more marked at the short end. For example, publication of the Governor/Chancellor minutes has led on average to an adjustment in short-term futures interest rates of over 3 basis points – not a large amount, but a significant spike nonetheless. More generally, the intra-day responses point towards transparency having clearly raised unconditional asset-price – in particular, interest-rate – volatility, in a way not likely absent these news releases. That is entirely in keeping with the results of theoretical analyses; it is in many ways a natural concomitant of greater transparency.
The really striking effects of transparency are found by looking at conditional term-structure variability. We again focus on a set of events: official interest-rate changes in the UK in the period before and after the introduction of the inflation target. We measure conditional variability by looking at the ‘surprise’ – or unexpected – component in the yield curve at the time of each official rate change. This allows us to condition on all information embodied in the yield curve up to the point of the rate change. Any surprises must therefore reflect news about the authorities' reaction function (path of future short-term rates). For example, in a world in which the authorities' reaction function was known with perfect certainty at every future date and was fully credible – reaction-function transparency was perfect – this interest-rate surprise would equal zero at all points along the yield curve. So improvements in transparency can be measured by the extent to which the economy is approaching that first-best.
We measure ‘surprises’ along the yield curve using the following set of regressions,[36]
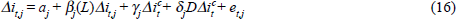
where j indexes the forward interest-rate maturity and t indexes
time. So Δit,j is the change in the j-periods
ahead (one-month) forward rate corresponding with official interest-rate change
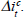 [37]
βj is a polynomial in the lag operator (L).
The lagged dependent variables here aim merely to mop up any remaining residual
autocorrelation. D is a regime-shift dummy, taking the value zero
in the pre-inflation target
regime (up to October 1992) and unity
thereafter.[38]
We measure surprises at 9 maturities along the yield curve: spot (1 month)
yields, and forward rates at 1 month, 3 months, 6 months, 2 years, 5 years,
10 years,
15 years and 20 years. For official interest rates,
[37]
βj is a polynomial in the lag operator (L).
The lagged dependent variables here aim merely to mop up any remaining residual
autocorrelation. D is a regime-shift dummy, taking the value zero
in the pre-inflation target
regime (up to October 1992) and unity
thereafter.[38]
We measure surprises at 9 maturities along the yield curve: spot (1 month)
yields, and forward rates at 1 month, 3 months, 6 months, 2 years, 5 years,
10 years,
15 years and 20 years. For official interest rates, 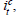 we use commercial
banks' base rate, which moves pari passu with the Bank
of England's official dealing rate in its open-market operations (Dale
1993). The sample period is January 1985 to March 1997, covering around 3,338
observations.
we use commercial
banks' base rate, which moves pari passu with the Bank
of England's official dealing rate in its open-market operations (Dale
1993). The sample period is January 1985 to March 1997, covering around 3,338
observations.
The key parameter vectors are γj and δj. The vector γj measures the mean interest-rate surprise at forward-rate maturity j measured over the full sample. Were an official rate change to be fully anticipated in existing market interest rates, then γ0 = 0: there would be no reaction in spot-market interest rates to the official interest-rate change. If the whole of the authorities' perceived reaction function was unaffected by the official interest-rate change – not just this period, but every period thereafter too – then γj = 0 for all j. There would be no forward-rate-curve – or expected reaction-function – surprise; transparency would be deemed perfect.
The vector δj measures the distinct effect of the move to an inflation target on mean interest-rate surprises. So δj = 0 for all j would be a rejection of the hypothesis that the move to an inflation target has had any effect on interest-rate surprises. Or, put differently, γj + δj measures the size of the mean interest-rate surprise along the yield curve during the inflation-target period.
Table 3 reports the empirical results. Looking first at the full-sample results – the vector γj – on average around 40 to 50 per cent of any official interest-rate change has been a surprise at the short end of the yield curve, judging by the behaviour of spot and short forward rates. The short-run surprise is also strongly significant. As we might expect, the size of the surprise is decreasing in j. But official rate changes also cause significant shifts along the rest of the yield curve. For example, at 2 years the surprise is around 25 per cent – half that at the very short end of the yield curve. And for j > 5 years, γj is negative. This pattern is exactly as we would expect if monetary policy is working in the desired fashion: raising short-term real interest rates, with a view to lowering expected inflation in the medium term. There is forward-rate pivoting. All in all, these results indicate that reaction-function transparency has been far from perfect on average over the period since 1985.
| Maturity j | Coefficients | R2 | D.W. | |||||
|---|---|---|---|---|---|---|---|---|
| αj | β1j | β2j | β3j | γj | δj | |||
| Spot | −0.10 (0.42) |
−0.13 (7.64) |
−0.15 (8.81) |
0.02 (0.98) |
0.46 (18.57) |
−0.41 (5.03) |
0.12 |
2.10 |
| 1 month | −0.13 (0.48) |
−0.23 (13.96) |
−0.14 (8.49) |
−0.06 (3.77) |
0.47 (16.70) |
−0.52 (5.79) |
0.13 |
2.10 |
| 3 months | −0.14 (−0.44) |
−0.26 (15.25) |
−0.13 (7.30) |
−0.07 (4.40) |
0.30 (9.42) |
−0.39 (3.73) |
0.09 |
2.09 |
| 6 months | −0.12 (0.47) |
−0.20 (11.66) |
−0.10 (5.64) |
−0.05 (2.88) |
0.35 (13.64) |
−0.29 (3.50) |
0.10 |
2.09 |
| 2 years | −0.17 (0.52) |
−0.39 (22.69) |
−0.07 (4.03) |
−0.04 (2.56) |
0.24 (7.41) |
−0.23 (2.22) |
0.15 |
2.02 |
| 5 years | −0.17 (0.61) |
−0.33 (19.45) |
−0.15 (8.49) |
−0.08 (4.57) |
0.14 (5.11) |
−0.16 (1.79) |
0.11 |
2.00 |
| 10 years | −0.13 (0.38) |
−0.50 (29.33) |
−0.31 (16.60) |
−0.10 (5.67) |
−0.13 (3.79) |
0.04 (0.32) |
0.22 |
2.02 |
| 15 years | −0.02 (0.05) |
−0.53 (30.64) |
−0.30 (15.80) |
−0.13 (7.54) |
−0.16 (3.49) |
0.05 (0.36) |
0.22 |
2.02 |
| 20 years | 0.07 (0.08) |
−0.58 (33.98) |
−0.36 (18.94) |
−0.18 (10.67) |
−0.08 (0.92) |
−0.01 (0.04) |
0.26 |
2.05 |
| Note: Numbers in parentheses are t-ratios. | ||||||||
The regime-shift effects embodied in δj are, however, the most striking diagnostic. The vector
δj is significant and negative at all maturities
up to around five years ahead. This indicates that the transparency innovations
which have accompanied the introduction of the UK's inflation-target regime
have had a significant impact in lowering the size of interest-rate forecasting
revisions. These regime-shift effects are large as well as significant. Empirically,
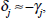 implying that surprises along the yield curve
are little different than zero during the inflation-target regime.
implying that surprises along the yield curve
are little different than zero during the inflation-target regime.
This is strong evidence to suggest that the transparency innovations accompanying the introduction of the UK's inflation target have reduced conditional term-structure variability – just as theory would predict. Those are effects we might reasonably expect to show up in other inflation-targeting countries, given the similar transparency innovations evident among them too. Their effect is clearly Pareto-improving. A stabler term structure ought to lower the risk premium and, in the long run, boost the capital stock. That capital-stock adjustment will be a long time coming. But its first manifestation – a stabler term structure – seems already to be evident.
5. Conclusions
A theme of this paper has been that the design of inflation targets is linked umbilically to the welfare costs of inflation. Some of those costs have been reasonably well-understood for some time and are quantifiable using the welfare-theoretic analysis of Bailey (1956). But the costs of unanticipated inflation, and the trade-off between inflation and output variability, are much less well researched in a welfare context. Because these costs determine the answers to such fundamental design questions as the optimal targeting horizon for monetary policy and the preferred degree of shock stabilisation, there is a pressing need for further work on them.
There is another, less tendentious, reason why some further quantification of the costs of inflation might be desirable. The price-stability consensus is now so deep-rooted that at some stage an intellectual backlash must be likely. There are echoes currently of the late 1920s, when there was a widespread consensus, intellectually and practically, favouring price stability. The experience of the Great Depression shattered that consensus. The influential recent contribution by Akerlof et al. (1996) is perhaps an early warning shot across the bows. Rebuffing that backlash calls for a reasoned quantification of the costs of inflation.
A second factor which might induce some unravelling of the price-stability consensus is demographics. The recent episode of global disinflation has come during a period when the policy-makers responsible can still remember high and volatile inflation. Many older-generation Germans, for example, still remember hyper-inflation. But that will not be the case for the next generation of policy-makers, whose collective will to fight inflation many hence be weakened. Shiller's (1996) survey of the general public found evidence of just this: inflation aversion was far greater among the old than among the young. That too might pose a risk to the price-stability consensus.
The best way of countering these inflation risks, and of ensuring a durable monetary framework, is by quantifying the costs imposed by inflation and, perhaps most important, explaining these costs to the public at large. In the past, central banks have performed poorly on both fronts. But recent transparency innovations – in particular among inflation targeters – offer some encouragement for the future.
Footnotes
I am grateful to my co-authors at the Bank of England – Glenn Hoggarth, Norbert Janssen, Vicky Read and Tony Yates – for allowing me to draw in places on on-going work in progress. They, together with Hasan Bakhshi, Darren Pain and Paul Tucker, provided useful comments on an earlier draft. My discussants, Don Brash and Guy Debelle, offered perceptive thoughts on the paper. The views expressed within are not necessarily those of the Bank of England. [*]
Of which there are now seven: Australia, Canada, Finland, New Zealand, Spain, Sweden and the United Kingdom. [1]
King (1996) defines an inflation-targeting reaction function in almost identical terms, comprising two components: a steady-state nominal anchor (the choice of π*); and an optimal short-run path for output and inflation (which is equivalent to choosing j in the feedback variable Etπt+j ). The choice of j may itself be state-contingent. [2]
A fourth issue – the choice of a feedback parameter γ – is not discussed, as this has a direct equivalence with the optimal targeting-horizon issue (the choice of j): that is, higher j (for given γ) is equivalent to smaller γ (for given j). [3]
These ranges are typically lower than in the US because, at present, price index weights in the US are only revised every ten years. This makes US consumer price indices more susceptible to outlet and substitution biases. For this reason, one of the recommendations of the Boskin Commission was to shorten the interval between revising price index weights in the US. [4]
This experiment is in line with that recently conducted by Feldstein (1996) for the United States. [5]
Though below we discuss some evidence on the welfare benefits of operating at the Friedman optimum and the costs of deflation. [6]
A practice which Ramsey (1928) described as ‘ethically indefensible’. Without such discounting, the welfare gains would, trivially, be infinite. [7]
Judson and Orphanides (1996) reach an identical conclusion – although both find decisive evidence of an adverse effect of inflation on growth at rates of inflation above 10 per cent. [8]
See also Fischer (1993) and Smyth (1994) for cross-section evidence on inflation-growth correlations. [9]
Assuming an interest elasticity of saving of zero. Feldstein (1996) assumes a higher saving elasticity as his main case and hence arrives at higher welfare benefits of around 1 per cent of GDP. [10]
For example, a fall in inflation from 4 per cent to 2 per cent in Dotsey and Ireland (1996) yields a welfare benefit of only 0.045 per cent of GDP (using currency as a metric and switching off the endogenous growth channel: Table 3). The corresponding gains when moving to the Friedman optimum are 0.24 per cent of GDP. [11]
Using an M1 specification for money. [12]
Assuming the same values of r and g as earlier. [13]
Indeed, it is arguable whether ex ante real interest rates can really ever be negative, without some extreme restrictions being placed on agents' utility functions. [14]
Others include time-dependent pricing rules, as in Ball, Mankiw and Romer (1988). [15]
With the smoothing parameter set equal to 1,600. This section draws on on-going work with Tony Yates. [16]
Also, for some of these countries the data sample is not as long as 30 years. We reach identical conclusions to those below if we use a broad (M2) measure of money instead of reserve currency. This section draws on joint work with Norbert Janssen and Glenn Hoggarth. [17]
The constant in the regression is insignificantly different from zero and the slope is insignificantly different from unity. [18]
The inflation term in Equation (1) is best thought of as an instantaneous rate. Were it a longer-horizon inflation rate, that would justify lengthening j. [19]
Svensson (1996) and Ball (1996b) add an extra lag to the IS curve and use an accelerationist Phillips curve with purely backward-looking expectations. But in all other respects their models are similar to the one used here. [20]
This is different from Equation (1) in that, for simplicity, it is defined in levels rather than first-differences. [21]
And for those countries where we have long runs of data, we do not have the periodicity of data – quarterly or more frequently – necessary to allow us to differentiate meaningfully between transmission lags across different inflation regimes. [22]
The analysis is no more than a first pass at the data: it looks at unconditional correlations, whereas ideally we would want to look at conditional correlations – the relationship between interest rate ‘shocks’ and inflation. [23]
In most empirical simulations, including those in Taylor (1993), it is the relative weight on output versus inflation in the policy rule which is altering as we move down the curve, not the targeting horizon. [24]
We would not necessarily expect this horizon to be state-invariant. The optimal targeting horizon is likely to depend also on the nature and persistence of shocks. [25]
Norway also publishes inflation forecasts. [26]
Because these are conditional inflation expectations formed by the authorities – rather than expectations formed by, say, the financial markets – a rule such as Equation (1) does not run into the nominal-indeterminacy problems discussed by Woodford (1994). [27]
Though such a path need not, in general, be unique. [28]
These literatures are not strictly separable, but we have treated them as such below. See Brunner (1981) and Goodfriend (1986) for excellent discussions of central banking and secrecy. [29]
Though, ultimately, Walsh (1995b) concludes the two are not isomorphic. [30]
See Briault, Haldane and King (1996) and Nolan and Schaling (1996) for a formalisation of this point. [31]
Tabellini (1987) develops a model with multiplicative uncertainty about the authorities' reaction function and learning. In this set-up, transparency reduces unconditional interest-rate variability. [32]
Haldane and Read (1997) develop an analytical model illustrating this point. [33]
These forward rates are extracted from estimated yield curves using the extended Nelson and Siegel methodology of Svensson (1994); see Deacon and Derry (1994). [34]
In the period prior to Bank of England independence. [35]
An extended analysis is presented in Haldane and Read (1997). [36]
The methodology here is similar to that in Cook and Hahn (1989) in a US context, except that we use a daily time series rather than explicit event-study approach, and use forward rates rather than yields to maturity. We look explicitly at one-month forward rates as this is (proximately) the interest-rate maturity of open-market operations in the UK over the period studied. In other countries, such as the US, an overnight forward rate might be more appropriate. [37]
We also include an impulse dummy variable for the ERM period. [38]
References
Abel, A. (1996), Comment on ‘The Costs and Benefits of Going from Low Inflation to Price-Stability’, M. Feldstein (1996), NBER Working Paper No. 5469, mimeo.
Akerlof, G.A., W.T. Dickens, and G.L. Perry (1996), ‘The Macroeconomics of Low Inflation’, Brookings Papers on Economic Activity, 1, pp. 1–76.
Almeida, A. and C.A.E. Goodhart (1996), ‘Does the Adoption of Inflation Targets Affect Central Bank Behaviour?’, London School of Economics, mimeo.
Andersen, P. (1992), ‘OECD Country Experiences with Disinflation’, in A. Blundell-Wignell (ed.), Inflation, Disinflation and Monetary Policy, Reserve Bank of Australia, Sydney, pp. 104–173.
Bailey, M. (1956), ‘The Welfare Cost of Inflationary Finance’, Journal of Political Economy, 64(2), pp. 93–110.
Bakhshi, H., A.G. Haldane, and N. Hatch (1996), ‘Some Costs and Benefits of Price-Stability in the United Kingdom’, Bank of England, mimeo.
Ball, L. (1994), ‘What Determines the Sacrifice Ratio?’, in N.G. Mankiw (ed.), Monetary Policy, University of Chicago Press, Chicago, pp. 155–182.
Ball, L. (1996a), ‘Disinflation and the NAIRU’, NBER Working Paper No. 5520.
Ball, L. (1996b), ‘Efficient Rules for Monetary Policy’, NBER Working Paper No. 5952.
Ball, L., N.G. Mankiw, and D. Romer (1988), ‘The New Keynesian Economics and the Output-Inflation Trade-Off’, Brookings Papers on Economic Activity, 1, pp. 1–65.
Barnett, W. (1980), ‘Economic Monetary Aggregates: An Application of Index Number and Aggregation Theory’, Journal of Econometrics, 14(1), pp. 11–48.
Barro, R.J. (1995), ‘Inflation and Economic Growth’, Bank of England Quarterly Bulletin, 35(2), pp. 166–176.
Barro, R.J. and D. Gordon (1983), ‘Rules, Discretion and Reputation in a Model of Monetary Policy’, Journal of Monetary Economics, 12(1), pp. 101–122.
Boskin Commission (1996), ‘Toward A More Accurate Measure of the Cost of Living’, Final Report to the Senate Finance Committee, Washington, D.C.
Briault, C.B. (1995), ‘The Costs of Inflation’, Bank of England Quarterly Bulletin, 35(1), pp. 33–45.
Briault, C.B., A.G. Haldane, and M.A. King (1995), ‘Independence and Accountability’, in I. Kuroda (ed.), Toward More Effective Monetary Policy, Bank of Japan, Tokyo, forthcoming.
Brunner, K. (1981), ‘The Art of Central Banking’, Centre for Research in Government Policy and Business, Working Paper No. 81-6.
Card, D. and D. Hyslop (1996), ‘Does Inflation “Grease the Wheels of the Labor Market”?’, NBER Working Paper No. 5538.
Cecchetti, S.G. (1995), ‘Inflation Indicators and Inflation Policy’, NBER Working Paper No. 5161.
Chadha, J., A.G. Haldane, and N.G. Janssen (1998), ‘Shoe-Leather Costs Reconsidered’, Economic Journal, (forthcoming).
Clark, P., D. Laxton, and D. Rose (1995), ‘Capacity Constraints, Inflation and the Transmission Mechanism: Forward-Looking Versus Myopic Policy Rules’, IMF Working Paper No. 95/75.
Cook, T. and T. Hahn (1989), ‘The Effect of Changes in the Federal Funds Rate Target on Market Interest Rates in the 1970s’, Journal of Monetary Economics, 24(3), pp. 331–351.
Cooley, T.F. and G.D. Hansen (1989), ‘The Inflation Tax in a Real Business Cycle Model’, American Economic Review, 79(4), pp. 733–748.
Cooley, T.F. and G.D. Hansen (1991), ‘The Welfare Costs of Moderate Inflations’, Journal of Money, Credit and Banking, 23(3), pp. 483–503.
Crawford, A. (1994), ‘Measurement Biases in the Canadian CPI: A Technical Note’, Bank of Canada Technical Report No. 64.
Crawford, A. and C. Dupasquier (1994), ‘Can Inflation Serve as a Lubricant for Market Equilibrium?’, in Economic Behaviour and Policy Choice Under Price Stability, Bank of Canada, Ottawa, pp. 49–80.
Cukierman, A. and A. Meltzer (1986), ‘A Theory of Ambiguity, Credibility and Inflation Under Discretion and Asymmetric Information’, Econometrica, 54(5), pp. 1099–1128.
Cunningham, A.W.F. (1996), ‘Measurement Biases in Price Indices: An Application to the UK's RPI’, Bank of England Working Paper No. 47.
Cutler, D., M.B. McClellan, J. Newhouse and D. Remler (1996), ‘Are Medical Care Prices Declining?’, NBER Working Paper No. 9570.
Dale, S. (1993), ‘The Effects of Changes in Official UK Rates on Market Interest Rates Since 1987’, The Manchester School, 61(1), pp. 76–94.
Deacon, M. and A. Derry (1994), ‘Estimating Market Interest Rates and Inflation Expectations from the Prices of UK Government Bonds’, Bank of England Quarterly Bulletin, 34(3), pp. 232–240.
Debelle, G. (1997), ‘Inflation Targeting in Practice’, IMF Working Paper No. 97/35.
Debelle, G. and D. Laxton (1996), ‘Is the Phillips Curve Really a Curve? Some Evidence from Canada, the United Kingdom and the United States’, IMF Working Paper No. 96/111.
Debelle, G. and G. Stevens (1995), ‘Monetary Policy Goals for Inflation in Australia’, in A.G. Haldane (ed.), Targeting Inflation, Bank of England, London, pp. 81–100.
Dolado, J.J., J.M. Gonzalez-Paramo and J. Vinals (1997), ‘A Cost-Benefit Analysis of Going from Low Inflation to Price Stability in Spain’, Banco de Espana, mimeo.
Dotsey, M. (1987), ‘Monetary Policy, Secrecy and Federal Funds Rate Behaviour’, Journal of Monetary Economics, 20(3), pp. 463–474.
Dotsey, M. and P. Ireland (1996), ‘The Welfare Cost of Inflation in General Equilibrium’, Journal of Monetary Economics, 37(1), pp. 29–47.
Duguay, P. (1994), ‘Some Thoughts on Price-Stability Versus Zero Inflation’, Bank of Canada, mimeo.
Driffill, J., G.E. Mizon and A. Ulph (1990), ‘Costs of Inflation’, in B.M. Friedman and F.H. Hahn (eds), Handbook of Monetary Economics, Volume 2, North-Holland, Amsterdam, pp. 1013–1066.
English, W.B. (1996), ‘Inflation and Financial Sector Size’, Board of Governors of the Federal Reserve System Finance and Economics Discussion Paper No. 96-16.
Feldstein, M. (1979), ‘The Welfare Cost of Permanent Inflation and Optimal Short-Run Economic Policy’, Journal of Political Economy, 87(4), pp. 749–768.
Feldstein, M. (1995), ‘Would Privatising Social Security Raise Economic Welfare?’, NBER Working Paper No. 5281.
Feldstein, M. (1996), ‘The Costs and Benefits of Going From Low Inflation to Price-Stability’, NBER Working Paper No. 5469.
Fischer, S. (1981), ‘Toward an Understanding of the Costs of Inflation: II’, Carnegie-Rochester Conference Series on Public Policy, 15, pp. 5–42.
Fischer, S. (1993), ‘The Role of Macroeconomic Factors in Growth’, Journal of Monetary Economics, 32(3), pp. 485–512.
Fischer, S. (1994), ‘Modern Central Banking’, in F. Capie, C. Goodhart, S. Fischer and N. Schnadt (eds), The Future of Central Banking: The Tercentenary Symposium of the Bank of England, Cambridge University Press, Cambridge, pp. 262–308.
Fischer, S. and F. Modigliani (1975), ‘Towards an Understanding of the Real Effects of the Costs of Inflation’, Weltwirtschaftliches Archiv, 114(4), pp. 810–833.
Fisher, I. (1911), The Purchasing Power of Money, MacMillan, New York.
Fuhrer, J. and B. Madigan (1994), ‘Monetary Policy When Interest Rates are Bounded at Zero’, Federal Reserve Bank of Boston Working Paper No. 94-1.
Freeman, R.T. and J.L. Willis (1995), ‘Targeting Inflation in the 1990s: Recent Challenges’, Board of Governors of the Federal Reserve System International Finance Discussion Paper No. 525.
Goodfriend, M. (1986), ‘Monetary Mystique: Secrecy and Central Banking’, Journal of Monetary Economics, 17(1), pp. 63–97.
Goodhart, C.A.E. (1994), ‘What Should Central Banks Do? What Should Be Their Macroeconomic Objectives and Operations?’, Economic Journal, 104(427), pp. 1424–1436.
Gordon, R. (1996), ‘Comment’ on Akerlof et al., Brookings Papers on Economic Activity, 1, pp. 60–66.
Groschen, E. and M. Schweitzer (1997), Inflation's Grease and Sand Effects in the Labour Market, paper presented at the NBER Conference, ‘Costs and Benefits of Achieving Price Stability’, New York.
Haldane, A.G. (ed.) (1995), Targeting Inflation, Bank of England, London.
Haldane, A.G. (1997), ‘On Inflation-Targeting in the United Kingdom’, Scottish Journal of Political Economy (forthcoming).
Haldane, A.G. and V. Read (1997), ‘Private Information and the Yield Curve’, Bank of England, mimeo.
Haldane, A.G. and C.K. Salmon (1995), ‘Three Issues on Inflation Targets’, in A.G. Haldane (ed.), Targeting Inflation, Bank of England, London, pp. 170–201.
Hall, S. and A. Yates (1997), ‘Are There Downward Nominal Rigidities in Product Prices?’, Bank of England Working Paper (forthcoming).
Hausman, J. (1997), ‘Cellular Telephones: New Products and the CPI’, NBER Working Paper No. 5982.
Judson, R. and A. Orphanides (1996), ‘Inflation, Volatility and Growth’, Board of Governors of the Federal Reserve System Finance and Economics Discussion Paper No. 96-19.
Keynes, J.M. (1923), A Tract on Monetary Reform, MacMillan, London.
King, M.A. (1994), ‘Monetary Policy in the UK’, Fiscal Studies, 15(3), pp. 109–129.
King, M.A. (1996), ‘How Should Central Banks Reduce Inflation? Conceptual Issues’, Bank of England Quarterly Bulletin, 36(4), pp. 434–448.
Kohn, D. (1995), ‘Comment’, in B. Bernanke and J. Rotemberg (eds), NBER Macroeconomics Annual, MIT Press, Cambridge, Massachusetts, pp. 227–233.
Laxton, D., G. Meredith and D. Rose (1995), ‘Asymmetric Effects of Economic Activity on Inflation’, IMF Staff Papers, 42(2), pp. 344–374.
Lebow, D.E., J.M. Roberts and D.J. Stockton (1992), ‘Economic Performance Under Price-Stability’, US Board of Governors of the Federal Reserve System Working Paper No. 125.
Leiderman, L. and L.E.O. Svensson (eds) (1995), Inflation Targets, CEPR, London.
LeRoy, S.F. and R.D. Porter (1981), ‘The Present-Value Relation: Tests Based on Implied Variance Bounds’, Econometrica, 49(3), pp. 555–574.
Longworth, D. and C. Freedman (1995), ‘The Role of the Staff Economic Projection in Conducting Canadian Monetary Policy’, in A.G. Haldane (ed.), Targeting Inflation, Bank of England, London, pp. 101–112.
Lucas, R.E. (1995), ‘On the Welfare Costs of Inflation’, Stanford University Center for Economic Policy Research Discussion Paper Series No. 394.
Lucas, R.E. (1996), ‘Monetary Neutrality’, Journal of Political Economy, 104(4), pp. 661–682.
Mayes, D. and B. Chapple (1995), ‘Defining an Inflation Target’, in A G Haldane (ed.), Targeting Inflation, Bank of England, London, pp. 226–245.
McCallum, B.T. (1983), ‘On Uniqueness in Rational Expectations Models: An Attempt at Perspective’, Journal of Monetary Economics, 11(2), pp. 139–168.
McCallum, B.T. (1995), ‘Inflation Targeting in Canada, New Zealand, Sweden, the United Kingdom, and In General’, in I. Kuroda (ed.), Toward More Effective Monetary Policy, Bank of Japan, Tokyo, forthcoming.
McCandless, G.T. and W.E. Weber (1995), ‘Some Monetary Facts’, Federal Reserve Bank of Minneapolis Quarterly Review, 19, pp. 2–11.
Mulligan, C.B. and X.X. Sala-i-Martin (1996), ‘Adoption of Financial Technologies: Implications for Money Demand and Monetary Policy’, NBER Working Paper No. 5504.
Nolan, C. and E. Schaling (1996), ‘Monetary Policy Uncertainty and Central Bank Accountability’, Bank of England Working Paper No. 54.
Nordhaus, W. (1994), ‘Do Real Output and Real Wage Measures Capture Reality? The History of Lighting Suggests Not’, Cowles Foundation Discussion Paper No. 1078.
Orphanides, A. and R.M Solow (1990), ‘Money, Inflation, and Growth’, in B.M. Friedman and F.H. Hahn (eds), Handbook of Monetary Economics, Vol. 1, North-Holland, Amsterdam, pp. 223–261.
Persson, T. and G. Tabellini (1993), ‘Designing Institutions for Monetary Stability’, Carnegie-Rochester Conference Series on Public Policy, 39, pp. 53–84.
Phelps, E.S. (1972), ‘Inflation in a Theory of Public Finance’, Swedish Journal of Economics, 75(1), pp. 67–82.
Rae, D. (1993), ‘Are Retailers Normal? The Distribution of Consumer Price Changes in New Zealand’, Reserve Bank of New Zealand Discussion Paper No. G93/7.
Ramsey, F.P. (1928), ‘A Mathematical Theory of Saving’, Economic Journal, 38(152), pp. 543–559.
Rogoff, K.S. (1985), ‘The Optimal Degree of Commitment to an Intermediate Monetary Target’, Quarterly Journal of Economics, 100(4), pp. 1169–1190.
Romer, C. and D. Romer (1996), ‘Federal Reserve Private Information and the Behaviour of Interest Rates’, NBER Working Paper No. 5692.
Rudin, J.R. (1988), ‘Central Bank Secrecy, “Fed Watching”, and the Predictability of Interest Rates’, Journal of Monetary Economics, 22(2), pp. 317–334.
Sarel, M. (1996), ‘Nonlinear Effects of Inflation on Economic Growth’, IMF Staff Papers, 43(1), pp. 199–215.
Sargent, T.J. and N. Wallace (1975), ‘Rational Expectations, the Optimal Monetary Instrument and the Optimal Money Supply Rule’, Journal of Political Economy, 83(1), pp. 241–254.
Shapiro, M.D. and D.W. Wilcox (1996), ‘Mismeasurement in the Consumer Price Index: An Evaluation’, NBER Working Paper No. 5590.
Shiller, R. (1996), ‘Why Do People Dislike Inflation?’, NBER Working Paper No. 5539.
Siklos, P. (1997), ‘Charting a Future for the Bank of Canada: Inflation Targets and the Balance Between Autonomy and Accountability’, in J. Grant, P. Howitt and P.L. Siklos (eds), Inflation Targets in Canada's Monetary Policy Regime, C.D. Howe Institute, Toronto.
Sims, C.A. (1992), ‘Interpreting the Macroeconomic Time-Series Facts: The Effects of Monetary Policy’, European Economic Review, 36(5), pp. 975–1011.
Smyth, D.J. (1994), ‘Inflation and Growth’, Journal of Macroeconomics, 16(2), pp. 261–70.
Summers, L.H. (1989), ‘How Should Long-Term Monetary Policy Be Determined?’, Journal of Money, Credit and Banking, 23(3), pp. 625–631.
Svensson, L.E.O. (1994), ‘Estimating and Interpreting Forward Interest Rates: Sweden 1992–93’, NBER Working Paper No. 4871.
Svensson, L.E.O. (1997), ‘Inflation Forecast Targeting: Implementing and Monitoring Inflation Targets’, European Economic Review, 41(6), pp. 1111–1146.
Tabellini, G. (1987), ‘Secrecy of Monetary Policy and the Variability of Interest Rates’, Journal of Money, Credit and Banking, 19(4), pp. 425–136.
Taylor, J.B. (1993), Macroeconomic Policy in the World Economy: From Econometric Design to Practical Operation, W.W. Norton, & Company, New York.
Todter, K-H. and G. Ziebarth (1997), ‘Price Stability Versus Low Inflation in Germany: An Analysis of Costs and Benefits’, Deutsche Bundesbank, mimeo.
Walsh, C.E. (1995a), ‘Optimal Contracts for Central Bankers’, American Economic Review, 85(1), pp. 150–167.
Walsh, C.E. (1995b), ‘Is New Zealand's Reserve Bank Act of 1989 an Optimal Central Bank Contract?’, Journal of Money, Credit and Banking, 27(4), pp. 1179–1191.
Woodford, N.G. (1994), ‘Non-Standard Indicators for Monetary Policy: Can Their Usefulness be Judged From Forecasting Regressions?’, in N.G. Mankiw (ed.), Monetary Policy, University of Chicago Press, Chicago, pp. 95–115.
Yates, A. (1995), ‘On the Design of Inflation Targets’, in A.G. Haldane (ed.), Targeting Inflation, Bank of England, London, pp. 135–169.
Yates, A. (1997), ‘What Goes Up Must Come Down: Downward Nominal Rigidities and Monetary Policy’, Bank of England, mimeo.