RDP 2024-04: Nowcasting Quarterly GDP Growth during the COVID-19 Crisis Using a Monthly Activity Indicator 3. Predicting Quarterly GDP Growth Using the MAI
July 2024
- Download the Paper 1.8MB
In this section we take the estimated MAI from the previous section and develop a framework for nowcasting quarterly growth in GDP. To achieve this goal, we will develop a regression model that relates the MAI to movements in quarterly GDP growth. This will require us to work with mixed frequency data.
3.1 Modelling mixed frequency data
When modelling time series of different frequencies, the typical thing to do is convert all time series to the lowest observed frequency using temporal aggregation. Usually this involves computing the average of the observations of the high-frequency variable that occur between samples of the low-frequency variable. For example, with monthly/quarterly data this could involve taking the average of the three months in the quarter or the last monthly observation in the quarter. The former was the approach adopted by previous studies in Australia including Gillitzer and Kearns (2007), Australian Treasury (2018), Panagiotelis et al (2019).[38] And while it is simple to implement, it discards potentially important information about the timing of movements in the high-frequency variable. Indeed, the reason we developed the MAI was so we could exploit the timely information it provides.
Instead, we will employ the MIDAS regression modelling framework (see Ghysels et al (2004) and Ghysels et al (2007)). MIDAS regression provides a flexible way to directly exploit all the information content of a higher-frequency explanatory variable to predict a lower-frequency dependent variable. It achieves this by using highly parsimonious distributed lag polynomials to prevent parameter proliferation that might otherwise occur.[39] MIDAS regression has been successfully used for predicting macroeconomic and financial variables. Of relevance to our work, Clements and Galvão (2008) show that using monthly information on the current quarter leads to significant improvements in forecasts based on coincident indicators.
An alternative approach that other researchers have used to handle mixed frequency data is to specify a state-space model and estimate it using the Kalman filter (e.g. Bok et al 2017).[40] However, in comparison with MIDAS models no clear ranking of forecast performance between the two methods was found (Bai, Ghysels and Wright 2013). Overall, Bai et al conclude that MIDAS and state-space models give similar forecasts.[41],[42]
The simple MIDAS model incorporating a single regressor is given by:
where and L1/m is a high-frequency lag operator such that with m indicating the higher sampling frequency of the explanatory variable (for example, m = 3 when x is monthly and y is quarterly). The intercept is specified by while the coefficient captures the overall effect of the high-frequency variable x on y and can be identified by normalising the function to sum to one. We assume the residuals, are an iid sequence with mean zero and constant variance. Finally, K is the maximum lag length for the included high-frequency regressor.
The method by which the MIDAS model achieves a parsimonious representation is via the lag coefficients in . This represents a set of weights as a function of a small dimensional vector of j parameters with . Two common functions used in empirical applications include the normalised exponential Almon lag function of Ghysels et al (2004) given as:
And the normalised beta function of Ghysels et al (2007) given as:
Note, Figure B1 illustrates examples of both polynomial weighting functions for different sets of parameters. Since both weighting functions are highly nonlinear, MIDAS models featuring either of them will need to be estimated by nonlinear least squares. An alternative specification proposed by Foroni et al (2015) is ‘unrestricted MIDAS’ (U-MIDAS). This method leaves the high-frequency lag coefficients unconstrained and can be estimated by OLS.[43] Foroni et al (2015) show that U-MIDAS is often preferable to standard (i.e. restricted) MIDAS (R-MIDAS) when modelling quarterly and monthly data because m is small. This reflects the fact that when the number of lags to model is relatively small, complications caused from having to estimate more parameters are reduced.[44] A U-MIDAS model with one explanatory variable is given as:
where and L1/m is defined as before. In any case, our x variable (i.e. the MAI) will be a latent common dynamic factor. MIDAS models incorporating factors are typically referred to as factor augmented MIDAS (FA-MIDAS) models and have been shown to perform well compared to more standard quarterly factor models in short-term forecasting of quarterly GDP growth in Germany (see Marcellino and Schumacher (2010)).[45] This finding is important for our work in two ways. It confirms the benefit to prediction from using mixed-frequency techniques and suggests that FA-MIDAS models can exploit time series information more efficiently than existing approaches.
Before we can move onto specifying a MIDAS model for nowcasting quarterly GDP growth using the MAI we need to decide on two aspects about the specification we intend to use. First, the functional constraints (if any) to implement and second, the optimal maximum lag order K. One way to address both issues is to use an information criterion to select the best model in terms of parameter restriction and the lag orders based on in-sample model fit.
Since the selected model will ultimately be used for nowcasting, we follow standard practice in the forecasting literature and use real-time data.[46],[47] For the dependent variable y we use first-release GDP from Lee et al (2012).[48] The main argument for this decision is that data revisions to GDP cause an additional issue when nowcasting. If we focus on current GDP, which is a combination of first release, partially revised and fully revised data, then we not only have to consider how to nowcast the first release of quarterly GDP growth but also how to predict future data revisions. Further, revisions to GDP can occur many quarters after the initial release. So, it is reasonable to assume analysts are more interested in the initial releases and concerned with the uncertainty related to nowcasting the first release than the uncertainty related to the revision process (Galvão and Lopresto 2020).
Unlike with GDP, there is no vintage targeted predictor dataset available for constructing a genuine real-time version of the MAI. However, as an alternative, we use the estimate of MAI produced by the Kalman filter for the reason previously discussed about it being more appropriate for prediction since it only incorporates information up to time t. Further, it is also conceptually similar to the definition of a real-time variable provided by Koenig et al (2003).[49]
We follow Foroni et al (2015) and use the BIC to evaluate a range of restricted and unrestricted MIDAS models. For the R-MIDAS models, we consider the normalised exponential Almon weighting function with j = 2 and j = 3 parameters. We also consider the normalised beta weighting function with j = 3 parameters. For all MIDAS model specifications, we specify four values for the maximum lag of the monthly explanatory variable (i.e. K ).[50] The results are presented in Table 2. The BIC strongly prefers the U-MIDAS specification with maximum lag K = 5, this is closely followed by the U-MIDAS model with maximum lag K = 6. Indeed, all U-MIDAS models are superior to the two R-MIDAS models except for when the maximum lag is two (K = 2). In this case, the R-MIDAS model using the normalised exponential Almon polynomial weighting function with two parameters (j = 2) is preferred.
In addition to comparing models based on the BIC, it is also possible to test the empirical adequacy of the polynomial weighting functions used with the R-MIDAS specifications under standard assumptions via a Wald-type test. The null hypothesis is that the functional restrictions are valid. Therefore, rejecting the null implies the functional restrictions are not supported by the data. By this metric, only one R-MIDAS model specification is consistent with the data, corresponding to the normalised exponential Almon polynomial weighting function with K = 2 and j = 2.
| Lag 0 : K |
Normalised exponential Almon | Normalised beta | U-MIDAS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| j=2 | j=3 | j=3 | |||||||||
| BIC | p-value | BIC | p-value | BIC | p-value | BIC | p-value | ||||
| 0:2 | 486.88 | 0.86 | 492.05 | 0.00 | 505.09 | 0.00 | 491.35 | na | |||
| 0:3 | 500.63 | 0.00 | 492.06 | 0.00 | 492.06 | 0.00 | 437.71 | na | |||
| 0:4 | 501.95 | 0.00 | 492.06 | 0.00 | 492.08 | 0.00 | 417.46 | na | |||
| 0:5 | 502.19 | 0.00 | 492.06 | 0.00 | 492.24 | 0.00 | 422.58 | na | |||
| Notes: The variable j is the number of parameters in the polynomial weighting function used in the MIDAS regression; the p-value is for the test of the null hypothesis of whether the restrictions on the MIDAS coefficients implied by the polynomial weighting function are supported by the data. Bold values denote best model. | |||||||||||
3.2 Out-of-sample prediction comparison
In this section we will assess the nowcasting performance of MIDAS models incorporating the MAI compared to standard benchmark models in a pseudo out-of-sample (OOS) comparison exercise. Based on the findings of the model evaluations presented in Table 2 we will only consider the FA-U-MIDAS specification for nowcasting quarterly GDP growth. However, instead of setting K = 5 as suggested by the BIC, we set K = 6. This choice is motivated by previous work (see Koening et al (2003) and Leboeuf and Morel (2014)) and because it covers the months most likely to affect quarterly GDP growth (i.e. three months of data covering the quarter for which we observe the last value of real GDP growth and the three months of data covering the first quarter to nowcast).[51]
We do not consider longer horizon predictions of quarterly GDP growth as in other studies. This is because predicting output growth over longer horizons is known to be much less reliable (e.g. Marcellino and Schumacher (2010) for FA-MIDAS models, Bańbura et al (2013) for factor models, and Chauvet and Potter (2013) for a systematic evaluation more generally). As such, the methods we develop here should only be thought of as short-term prediction devices.
An important advantage of MIDAS regression over other methods used for handling mixed frequency data (i.e. temporal aggregation) is that it allows us to make predictions within periods. Further, each successive prediction will incorporate a new estimate of the MAI as more data becomes available in the quarter. For simplicity, we assume the following timing of data releases. Let yt denote the current quarter of quarterly GDP growth and yt+1 denote the next quarter of quarterly GDP growth. The first release of GDP for quarter t contains data up to quarter t – 1. Before data on GDP growth for t become available in quarter t +1, we will have four updates of the MAI. First estimate of the MAI incorporating monthly data up to t –1 in t –2/3 (i.e. first month of current quarter), second estimate of the MAI incorporating monthly data up to t –2/3 in t –1/3 (i.e. second month of current quarter), third estimate of the MAI incorporating monthly data up to t –1/ 3 in t (i.e. end of the current quarter). Finally, a fourth estimate of the MAI incorporating monthly data up to t in t +1/3 (i.e. first month of the next quarter). The timing of these monthly updates of the MAI allows us to produce four predictions of quarterly GDP growth in the current quarter which we label as i) forecast (FC), ii) nowcast in month 1 (M1), iii) nowcast in month 2 (M2), and iv) nowcast in month 3 (M3).[52] See Figure 4 for a visual summary.
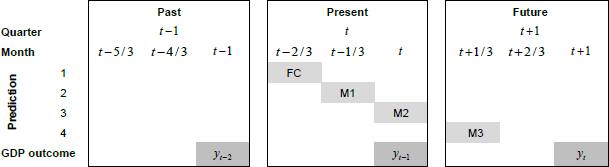
Based on this, the general FA-U-MIDAS model we use in the OOS evaluation becomes:
where yt is first-release quarterly GDP growth, xt is the MAI and depending on the monthly flow of data during the quarter (i.e. corresponding to the four predictions: FC, M1, M2, M3, in that order). Hence, as new monthly estimates of the MAI are produced during the quarter, the specification of the FA-U-MIDAS model will change with an increasing number of regressors. For example, when i =3 (i.e. FC), the FA-U-MIDAS model for current quarterly GDP growth consists of an intercept and three months of data on the MAI from the previous quarter:
Alternatively, when i =0 , the model expands to include three additional months of data on the MAI from the current quarter (reflecting the full model):
Note, for ease of notation, we drop the superscript (m) from the x variable in both equations. Across the OOS evaluation period we will keep the FA-U-MIDAS model specification fixed to this general form.[53] Further, we will compare the four FA-U-MIDAS model specifications to two standard models used in previous OOS forecasting/nowcasting evaluation exercises. These include the sample mean and an AR(1) process (see Australian Treasury (2018) and Panagiotelis et al (2019) for the sample mean and Gillitzer and Kearns (2007) for the AR(1) process). The sample mean has been shown to be a formidable forecasting model for quarterly growth in GDP (Panagiotelis et al 2019) and will serve as our benchmark model in our comparisons. Additionally, we also consider a model based on a quarter average (QA) measure of the MIA as a crosscheck.[54] The QA model includes a temporal aggregated value of the MAI for the current quarter and another lagged value for the previous quarter, making it similar to M3.
To evaluate the performance of the various models, we carry out a recursive estimation and forecast/nowcasting exercise, where the full sample is split into estimation and evaluation sub-samples. The estimation sample initially covers the period 1978:Q2–1988:Q1 (i.e. R = 40 or 10 years, similar to Panagiotelis et al (2019)) and is expanded by one quarter at a time and the model parameters are re-estimated each time. The evaluation sample is between 1988:Q2 and 2022:Q2 (i.e. P =137 ). For each quarter in the evaluation sample, we want to compute a forecast and three nowcasts depending on the monthly information set. For example, for the initial evaluation quarter 1988:Q2, we want to compute a forecast using data up to 1988:Q1 (FC) and then a nowcast in 1988:M4 (M1), 1988:M5 (M2) and 1988:Q2 (M3). At this point we also compute the sample mean and AR(1) forecasts. The predictions from each model over the evaluation sample are presented in Figure 5.
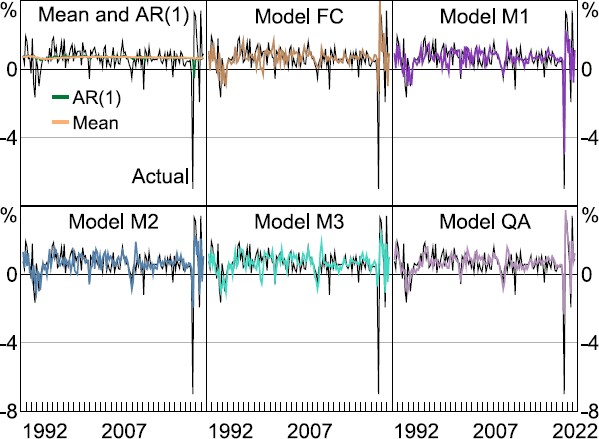
Note: GDP is first release.
Sources: ABS; Authors' calculations; Lee et al (2012).
The sample mean and AR(1) predictions are very similar given the lack of persistence in quarterly GDP growth, although the AR(1) model was slightly better at predicting the COVID-19 decline in 2020:Q2, albeit with a quarter lag. Since both models are estimated using quarterly data, neither were able to fully anticipate the significant fall and immediate rise that eventuated in 2020:Q2 and 2020:Q3. In contrast, the models incorporating monthly information performed much better. Predictions from each model are reasonably similar in the period before the COVID-19 crisis, but all models show noticeable differences in the period afterwards. For example, model M1 was most accurate in predicting the contraction in quarterly GDP growth in 2020:Q2, although it was still off by around 2 percentage points. Alternatively, model M3 was relatively less successful. This is surprising, since model M3 has two extra months of data on 2020:Q2 and previous research has shown that having more timely data usually improves forecast accuracy.[55] One explanation could be that model M3 has two additional parameters to estimate compared to model M1 and increased estimation uncertainty could be affecting the model's accuracy.
In relation to predicting the large subsequent upswing in quarterly GDP growth in 2020:Q3, more success was achieved by models FC and QA. This is also surprising since both models contain less information on the quarter compared to the three ‘M’ models. However, both models have less parameters to estimate compared to the other models (FC with three and QA with only two) and therefore could be more precisely estimated, improving the accuracy of both models.
We assess point forecast/nowcast accuracy of each model considered using standard root mean squared error (RMSE) defined as:
where is the forecast/nowcast produced by one of the models and P is the number of predictions being assessed. We compare RMSEs over three different horizons: the past three years, the past ten years, and the full evaluation sample period. We do this comparison for the full sample which includes the COVID-19 period as well as a sample that ends in 2019:Q4, excluding the effects of the COVID-19 crisis as a robustness check. The results are presented in Table 3 which provides both the raw RMSEs for each model computed using Equation (12) as well as the RMSE for each model relative to the sample mean model. A relative RMSE greater than one implies the model's predictions are less accurate compared to the benchmark model while a relative RMSE less than one implies the model's predictions are more accurate than the benchmark model.[56]
For the full sample period, model M1 outperforms all other models across each of the three horizons. In relative terms, model M1's RMSEs are over half of those of the sample mean model across the past three-year and ten-year periods and just under three-quarters of the benchmark model for the full sample. The QA model was the only other model that achieved a similar level of performance for the full sample horizon. As previously discussed in relation to Figure 5, this result is primarily because of how well model M1 predicted the significant decline in quarterly GDP growth that occurred in 2020:Q2. This is supported by comparing the model RMSEs in the pre-COVID-19 period. Here, there is no one model that outperforms the others in all periods as was the case when the COVID-19 period was included. Further, all model RMSEs are notably lower and much closer together as well. The models incorporating monthly information are not as dominant either. Indeed, the three ‘M’ models are outperformed by the sample mean model in both the shorter three-year and longer full sample horizons. In contrast, the QA model does narrowly outperform the benchmark model across all three horizons, suggesting that there is always some benefit to using timely information to make predictions. However, it also suggests that there might exist a trade-off between model size and accuracy, especially when making predictions during relatively ‘normal’ periods.
| Sample mean | AR(1) | FC | M1 | M2 | M3 | QA | |
|---|---|---|---|---|---|---|---|
| Full sample | |||||||
| Root mean squared error | |||||||
| Past three years | 2.72 | 2.83 | 2.11 | 1.24 | 1.72 | 2.23 | 1.49 |
| Past ten years | 1.52 | 1.58 | 1.19 | 0.74 | 1.00 | 1.26 | 0.87 |
| All | 0.98 | 1.01 | 0.87 | 0.70 | 0.78 | 0.88 | 0.70 |
| Relative root mean squared error | |||||||
| Past three years | na | 1.04 | 0.77 | 0.45 | 0.63 | 0.82 | 0.55 |
| Past ten years | na | 1.04 | 0.79 | 0.49 | 0.65 | 0.83 | 0.57 |
| All | na | 1.03 | 0.89 | 0.71 | 0.79 | 0.89 | 0.71 |
| Pre-COVID-19 sample | |||||||
| Root mean squared error | |||||||
| Past three years | 0.30 | 0.30 | 0.35 | 0.34 | 0.33 | 0.36 | 0.29 |
| Past ten years | 0.46 | 0.47 | 0.45 | 0.43 | 0.45 | 0.46 | 0.45 |
| All | 0.59 | 0.59 | 0.64 | 0.62 | 0.61 | 0.60 | 0.56 |
| Relative root mean squared error | |||||||
| Past three years | na | 1.00 | 1.18 | 1.15 | 1.10 | 1.21 | 0.98 |
| Past ten years | na | 1.03 | 0.98 | 0.94 | 0.97 | 1.01 | 0.97 |
| All | na | 1.00 | 1.09 | 1.06 | 1.05 | 1.03 | 0.96 |
| Notes: Relative to sample mean model. Full sample: 1988:Q2–2022:Q2; pre-COVID-19 sample: 1988:Q2–2019:Q4. Bold values denote best model(s) for each horizon. | |||||||
When comparing our results to those of previous studies related to forecasting/nowcasting quarterly GDP growth, it is only fair to focus exclusively on our pre-COVID-19 sample results. In this light, our results still show a clear benefit to using higher frequency (monthly) data for predicting lower frequency (quarterly) data. Both Australian Treasury (2018) and Panagiotelis et al (2019), who each focus on quarterly data, are unable to consistently outperform the sample mean benchmark model. However, Australian Treasury's model can beat the sample mean model once all data on the current quarter are available (the timing of which would be comparable to our M3 and QA models). In contrast, all FA-U-MIDAS models except M3 outperform the sample mean model on average over the last ten years, while the QA version shows outperformance across this timeframe as well as over the last three years and full sample (1988:Q2–2019:Q4).
3.3 Evaluating model performance during the COVID-19 crisis
As shown in Table 3, the three-year horizon which covered the COVID-19 crisis shows substantial divergence in the accuracy of model predictions incorporating monthly and quarterly information. Most of this outcome can be attributed to one time point: June 2020 – the quarter that experienced the brunt of the initial government-mandated COVID-19 lockdowns and the subsequent disruption to economic activity that resulted. The prediction error generated for each model relative to the actual first-release quarterly GDP growth outcome for that period is presented in Figure 6. A value above one means the prediction error was larger than the actual GDP outcome, while a value less than one signifies the prediction error was smaller than the actual GDP outcome.
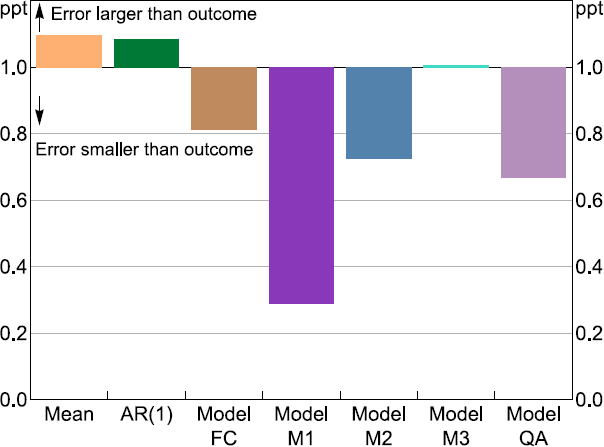
Note: Errors are relative to first-release quarterly GDP growth in 2020:Q2 (–7 per cent).
Figure 6 helps illustrate how incorporating high frequency (monthly) information greatly improved forecast/nowcast performance for most FA-U-MIDAS model predictions for this quarter, especially model M1 (which includes the month of April 2020 in its nowcast). Model M1 achieved a nowcast error equivalent to roughly one-quarter of the size of the eventual downturn that occurred in quarterly GDP growth (–7 per cent). What is crucial about this from a policymaker's perspective is the nowcast from model M1 was capable of being generated midway through the quarter in question – almost three months before the official figure on GDP would finally be published. Thereby giving policymakers a very timely reading on how the COVID-19 crisis was affecting activity.
Like with the prediction results, the errors for models M2 and M3, which include more timely information, are also both substantially larger than model M1. The performance of the QA model, which uses a temporal aggregated version of the MAI (i.e. three-month average), appears to strike a compromise between the three MIDAS models; suggesting there might be situations when it is beneficial to use temporal aggregated regressors in models, potentially in cases when the model might be otherwise over-parameterised. However, our key result that incorporating timely information can improve model prediction accuracy during downturns corresponds to previous work including Clements and Galvão (2009) (the US recession in 2001), Schorfheide and Song (2015) (the GFC impact on US economic activity in 2008) and Jardet and Meunier (2022) (the COVID-19 pandemic's effect on world GDP growth).
3.4 Assessing the predictive content of the MAI
The relative RMSE results in the previous section indicate that models incorporating monthly information generate more accurate predictions (and smaller errors) compared to the baseline sample mean model. However, to be definitive, it is important we compare model performance using a formal statistical test of equal predictive accuracy.
We cannot use the well-known Diebold-Mariano-West (DMW) t-type test for equal predictive accuracy since we are evaluating nested models (all models include an intercept). Instead, we follow the approaches of Clark and McCracken (2005) and Clements and Galvão (2009) and implement the bootstrap version of the MSE-F test of equal mean squared error (MSE) developed by McCracken (2007).[57] Let MSEi denote the MSE from model i for , then the test of equal predictive accuracy of the benchmark sample mean model (i.e. ) and the alternative model specifications considered are implemented using the following test statistic:
where P is the number of predictions being compared. A negative MSE-F implies that model i is less accurate compared to the sample mean model, whereas a positive MSE-F means the model i is more accurate. The bootstrap is used to compute the p-value for the MSE-F test and proceeds as follows. The sample mean model is estimated using the whole sample period of first-release quarterly GDP growth (as recommended by Clements and Galvão (2009)). From the model fit we take the estimated intercept and the variance of the residuals and simulate multiple time series trajectories from the sample mean model assuming Gaussianity.[58] For each one of the simulated time series trajectories, we apply the same recursive estimation and prediction steps we used with the actual data to calculate the MSE-F statistic for that replication. Note, the MAI is held fixed in each replication. We set the total number of replications in the bootstrap procedure to 1,000. The empirical p-value is calculated as the proportion of MSE-F statistics from the simulations that are larger than the MSE-F statistic computed using actual data. We implement the bootstrapped MSE-F test for the full sample including the COVID-19 period and a shorter sub-sample excluding the COVID-19 period as we did in relation to the RMSE comparisons in Table 3. The results are presented in Table 4.
| Sample mean | AR(1) | FC | M1 | M2 | M3 | QA | |
|---|---|---|---|---|---|---|---|
| Test statistic | |||||||
| Full sample | na | −7.12 | 36.43 | 132.87 | 80.47 | 34.86 | 135.34 |
| Pre-COVID-19 | na | −0.20 | −19.77 | −14.29 | −11.53 | −7.71 | 11.47 |
| Empirical p-value | |||||||
| Full sample | na | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Pre-COVID-19 | na | 0.18 | 0.98 | 0.68 | 0.38 | 0.10 | 0.00 |
|
Notes: Benchmark model is the sample mean. Empirical p-value computed by bootstrap using 1,000 replications. Full sample is 1988:Q2–2022:Q2; pre-COVID-19 sample is 1988:Q2–2019:Q4. Bold values denote rejection of the null hypothesis. |
|||||||
The MSE-F test results confirm the findings in Table 3 and they also differ depending on whether the test is conducted on the full sample or the pre-COVID-19 sample. For the full sample we strongly reject the null hypothesis of equal predictive accuracy in relation to the sample mean model and all four FA-U-MIDAS models incorporating monthly information. However, the same is not true for the pre-COVID-19 sample, where the null is only rejected for model QA (although model M3 is borderline at the 10 per cent level).[59]
Overall, these results mirror those of Chauvet and Potter (2013) and Siliverstovs (2020) that relate to the accuracy of model predictions of quarterly GDP growth in the United States changing between expansions and recessions. In our case, the statistical evidence favouring models incorporating more timely information over simpler models based on quarterly information is mostly due to significant outperformance during the three-year period covering the COVID-19 crisis. In contrast, during more ‘normal’ times, the model predictions incorporating monthly information fail to meaningfully improve on those of the benchmark sample mean model. Considering Figure A3, this is not surprising. Australian quarterly GDP growth is serially uncorrelated. However, model QA which includes some information on the current quarter (albeit averaged), was able to consistently outperform the benchmark model in both sample periods. This suggests there might be a trade-off between incorporating more timely information and increasing model complexity.
Footnotes
In addition, Richardson, van Florenstein Mulder and Vehbi (2021) for New Zealand; however, Anthonisz (2021) is an exception. [38]
MIDAS regression implements a form of temporal aggregation, but unlike using the average for example, the weights used by the model are entirely determined by the data. For an introduction to MIDAS regression for macroeconomic prediction see Armesto, Engemann and Owyang (2010). [39]
In this approach, quarterly GDP growth is included as an extra observable in the measurement equation in Equation (2) when estimating the factor model specified with monthly frequency data. This interpolates quarterly GDP growth across the three months in quarter. [40]
In most cases, the state-space model was a little more accurate, but it is also computationally more demanding. [41]
In related work, Schorfheide and Song (2015) show that predictions of real US GDP growth from a mixed frequency VAR model are empirically similar to those obtained from an (unrestricted) MIDAS regression. [42]
This allows for greater flexibility in how the weights used in temporal aggregation are determined by the data and is reminiscent of the mixed frequency distributed lag method introduced earlier by Koenig et al (2003). [43]
However, when the difference in frequencies is large, Foroni et al (2015) find that R-MIDAS outperforms U-MIDAS. [44]
In their analysis the authors also compared a two-step approach (first estimate monthly factors and then estimate the forecast of quarterly GDP growth using a FA-MIDAS model) to an integrated approach (estimate monthly factors and then forecast using a state-space model). They conclude that the two approaches produce similar forecasts, and therefore supports the findings of Bai et al (2013) and our decision to focus on MIDAS models instead of a state-space framework. Further, the best performing model in many cases was found to be a simple MIDAS structure without a distributed lag term and only one lag of the latent factors. [45]
As noted by Clements and Galvão (2009), there are two ways of using vintage data to estimate a model in real time. First, use the ‘end-of-sample’ vintage. In this case, for each t the most current vintage data are used to estimate the model. Second, use ‘real-time’ vintage data. Under this approach, for each t the initially available data are used to estimate the model. This approach was introduced by Koenig et al (2003) to overcome an issue with the first method. The problem is that any given vintage of data will be a combination of first releases, partially revised and fully revised data. Koenig et al claim that model parameters estimated using the first method will be inconsistent. Importantly, the results of Koenig et al and Clements and Galvão (2008) suggest the real-time vintage method produces more accurate predictions of output growth in the United States using distributed lag and MIDAS models. [46]
A notable exception is Panagiotelis et al (2019), who only consider current vintage data in their work. [47]
This is also comparable to Koenig et al (2003) in relation to forecasting US quarterly GDP growth and Galvão and Lopresto (2020) in relation to nowcasting UK quarterly GDP growth. [48]
The steps we follow to estimate the real-time MAI is as follows. First, we estimate all the parameters of the model using the QMLE method. Second, we take the final parameter estimates and re-run the Kalman filter again using those parameter values and the targeted predictor dataset. [49]
All estimation was done in R using the ‘midasr’ package of Ghysels, Kvedaras and Zemlys (2016). [50]
As already noted, the BIC ranks the U-MIDAS model with six lags second in terms of model suitability. [51]
Predictions made using M3 are sometimes labelled as ‘backcasts’, that is, those that are backwards looking or that are made (shortly) after the end of the quarter of interest (see Siliverstovs (2020) and Chinn, Meunier and Stumpner (2023), who both use the same four-period horizon). [52]
This MIDAS model framework is reminiscent of Koenig et al (2003) and Leboeuf and Morel (2014), who both also use fixed model specifications in their work. [53]
The QA model is a special type of R-MIDAS model in which the weights are constrained to be uniform (i.e. equal to 1/3 in each month). Further, uniform weights are equivalent to the normalised exponential Almon function with the first parameter set to 1 and the rest set to 0 and the normalised beta function with all parameters set to 1. [54]
One exception is Chinn et al (2023), who also do not find a uniform improvement in accuracy as more information becomes available when nowcasting world trade volumes using a similar four-horizon setting. [55]
Note that an RMSE close to one implies the uncertainty in the model's prediction is comparable to the variability of quarterly GDP growth since the unconditional sample standard deviation of quarterly growth is approximately one over the sample period we work with. [56]
Simulations conducted in Clark and McCracken (2005) show that MSE-F bootstrap critical values yield better size results compared to those based on asymptotic critical values. West (2006) also recommends using the bootstrap when testing for differences in MSEs between nested models. Additionally, Clark and McCracken (2005) show the MSE-F test is more powerful than t-type counterparts (such as the DMW test). The reason for this is because, under the alternative hypothesis, the F-type test statistic diverges to infinity at a faster rate. [57]
In this way the trajectories are generated under the null hypothesis the nesting models have similar accuracy as the benchmark sample mean model. [58]
Note, the null is never rejected for the sample mean and AR(1) models, indicating that there really is no statistical difference between the two models. [59]