RDP 2024-04: Nowcasting Quarterly GDP Growth during the COVID-19 Crisis Using a Monthly Activity Indicator 2. Monitoring Activity Using a Combination of Targeted Monthly Indicators
July 2024
- Download the Paper 1.8MB
To construct the MAI, we apply a DFM to a monthly dataset. The dataset will be comprised of series which show a statistically significant relationship with quarterly GDP growth since this is our variable of ultimate interest. We first discuss the monthly dataset and how we select the series it contains before describing the DFM method and estimation results.
2.1 Monthly activity dataset
The choice of dataset to use when estimating a DFM is an important part of the process that is often underappreciated. There no single agreed upon way to do this in the literature. Indeed, different datasets can result in different factor estimates even when using the same estimation technique (Bai and Ng 2008). Given this, there is a tendency for researchers to select as many series as possible in the attempt to capture all available information. However, having too many series can be problematic for factor estimation as well; especially if many of the series in the dataset are ‘noisy’ (Boivin and Ng 2006).[14]
Relatedly, other methods for creating datasets from pre-selected series have been proposed to generate more accurate forecasts with factor-augmented regressions. Unlike those proposed by Boivin and Ng (2006), these methods recommend estimating a factor model using a dataset comprised of only those series shown to have predictive power for a ‘target’ variable of interest. Importantly, these so-called ‘targeted predictors’ explicitly take account of the object of interest which other methods do not. Two prominent strategies include ‘hard’ and ‘soft’ thresholding to determine which variables the factors are to be extracted from (Bai and Ng 2008). Under hard thresholding, the predictors are ranked based on a pre-test procedure and those that fail to meet some criteria are discarded from the dataset. Under soft thresholding, a portion of top ranked predictors are kept, where the ordering of the predictors depends on the soft thresholding rule used. Bai and Ng (2008) show that factors extracted from a dataset of targeted predictors can result in superior forecasting performance.[15]
To begin, we compile an ‘extended’ dataset that includes 53 monthly partial indicators covering various aspects of the Australian economy. Following Bańbura and Rünstler (2007) we group these series into three main categories: ‘hard’ (30 per cent; includes series covering key measures of activity such as the labour market); ‘soft’ (36 per cent; includes survey measures which tend to be more timely than hard series); and ‘financial’ (34 per cent; includes series such as interest rates, equity prices and commodity prices). When available, we include both aggregate and disaggregate measures in the dataset (i.e. total credit as well as its sub-components). Some researchers argue against this practice; however, the method we use to estimate the DFM is robust to including aggregate and disaggregate series.[16] The dataset covers the sample period 1978:M2 to 2022:M9 and was influenced by the number of series available in the early part of the sample.[17] However, several series in the dataset have later starting and earlier ending periods due to being relatively new, so the resulting dataset is ‘unbalanced’ or ‘ragged edge’.
Before using the dataset, we transform all series to be stationary and standardise them to have zero mean and unit variance as is common in the factor modelling literature. Series are made stationary by taking logs and/or first differences as appropriate (see Table A1 for details). When doing the standardisation, rather than use the full sample mean, we instead follow Kamber, Morley and Wong (2018) and implement ‘dynamic demeaning’ for each series using a rolling 20-year backward-looking estimate of the sample mean as a way of controlling for potential structural breaks in the central tendency of each series over the sample period the dataset covers. The decision to use a 20-year window (instead of a 10-year window as in Kamber et al (2018)) is because until the COVID-19-induced recession in 2020, the length of the business cycle in Australia was arguably longer than elsewhere.[18]
Since our main goal is to produce a monthly activity indicator for monitoring the economy at a higher frequency than is currently possible and to predict quarterly GDP growth in the near term, we will follow Bai and Ng (2008) and implement a pre-selection strategy to our extended dataset to remove any uninformative predictors in relation to quarterly GDP growth. Because our dataset is unbalanced, we will use their hard thresholding strategy. This involves running a series of separate regressions of the target on a single predictor. Each regression includes a set of controls comprised of an intercept and lags of the target variable which are the same for all regressions. The predictors are then ranked in descending order by the magnitude of the coefficient t-statistic on each predictor. Any predictor with a test statistic below some specified threshold significance level is discarded.[19],[20]
The method we use to estimate the DFM is robust to model misspecification. Hence, one could argue there is no need to apply any pre-selection to the dataset since the model will assign the right weight to each series (see Bańbura et al (2013)). However, factors extracted from the extended dataset will, by construction, be a linear combination of all series in the dataset. Some of these series might not be very informative about quarterly GDP growth but will still have some effect on the model outputs even if small. That is, no series is likely to be assigned a zero weighting. Therefore, it makes sense to only focus on a subset of series found to be informative about the quarterly growth in GDP.[21]
Instead of using the current release version of GDP, which is a combination of first release, revised and fully revised data (Stone and Wardrop 2002), we follow Koenig, Dolmas and Piger (2003)'s recommendation and use the first-release version of GDP (Lee et al 2012). We extend Bai and Ng (2008)'s hard-thresholding algorithm (which only considers variables at a quarterly frequency) to a mixed frequency setting. This is because our target variable is quarterly while our predictors are monthly. In this situation, it is typical to perform some type of temporal aggregation such as taking the quarter average (i.e. each quarterly observation is the average of the three monthly observations in each quarter). However, this could result in a potential loss of information. Instead, each monthly series is converted to a quarterly series by stacking the first, second and third months in each quarter as three separate quarterly series.[22]
Because we have three predictors (i.e. one series each for the first, second and third months of the quarter) instead of only one as in Bai and Ng (2008) and Bulligan et al (2015), we cannot implement the same t-statistic to test for significance and rank series as they both do. Instead, we test for the joint (linear) significance for all three series at once using a Wald statistic calculated using a HAC robust covariance matrix. As controls we include an intercept and, as our sample covers the COVID-19 crisis period, a set of seven indicator variables for the periods 2020:Q2 to 2021:Q2 and 2021:Q4.[23] The indicator variables were included to account for the COVID-19 crisis so as not to affect the test results and series ranking.[24] When running each regression, we adjust the dependent variable's sample length to match the sample length of each predictor which varies by series. Because our extended dataset is already relatively small by international standards, we use a less restrictive significance level of 10 per cent to gauge significance.[25] While this is higher than the standard 5 per cent, it helps ensure we have a reasonable sized subset of the extended dataset.
The outcome from the hard thresholding procedure is a dataset of 30 variables from the original 53-variable extended dataset.[26] Of the three categories, ‘soft’ is the dominant one with 13 series (43 per cent); followed by ‘financial’ with 9 (30 per cent) and ‘hard’ with 8 (27 per cent). Figure A1 shows the 30 series by category and ranked by Wald statistic along with the threshold critical value (dashed line). The number of series in the targeted predictor dataset is comparable to the minimum suggested by Bai and Ng (2008) and is slightly larger than the 24 series used in the empirical application by Bańbura et al (2013) and slightly smaller than the 37 series used by Australian Treasury (2018). Further, Panagiotelis et al (2019) mention they find no benefit from considering an information set bigger than 20 to 40 variables when forecasting Australian macroeconomic time series such as quarterly GDP growth.[27]
2.2 Constructing the monthly activity indicator using a dynamic factor model
DFMs are a popular statistical model for summarising the common (linear) variation contained in a panel of time series data and prediction. A key issue of all these previous works is that they not true DFMs as per Bai and Wang (2015). Instead, we estimate the MAI using the general form of the DFM defined as:
where yt is a N × 1 vector of weakly stationary targeted predictors, ft is a q × 1 vector of the dynamic factors, and is the dynamic factor loadings for ft–i with i = 0, 1,...,s and t = 1,...,T. Together, the factors and loadings provide a measure of the common variation shared across series in the dataset. The dynamic factors are modelled as a VAR(p) process with a q × q matrix of autoregressive coefficients (with all roots outside the unit circle). The number of dynamic factors is q (the dimension of ft).
The covariance matrix of the idiosyncratic component is given by R with dimension N × N and is restricted to be a diagonal matrix. In the state equation, the covariance matrix of corresponds to the q × q matrix Q . We assume that (i.e. the two noise processes are independent). This specification of the DFM has two different sources of dynamics. First, there are s lagged factors representing a dynamic relationship between the observable series yt and the factors ft. Second, the dynamics of the factors are assumed to be captured by a VAR(p) process.[28] Bai and Wang (2015) argue that it is the first source of dynamics that makes this specification a true dynamic factor model because it is these dynamics that make the biggest distinction between dynamic and static factor analysis.[29]
We estimate the DFM by quasi-maximum likelihood (QMLE).[30] Estimation is conducted via the expectation-maximisation (EM) algorithm and consists of two parts. First, we estimate the factors given the data by running the Kalman filter and Rauch-Tung-Striebel (RTS) smoother recursions (the ‘E-step’). Second, we use the estimated factors from the previous step to compute the model parameters by maximising the expected log-likelihood by regression (the ‘M-step’). This requires us to re-cast Equation (1) into its state-space representation given as:
The measurement equation takes the form of a static factor model (Stock and Watson 2002) with r = q (s + 1) static factors. Let k = max(p, s + 1), then Ft is a qk × 1 vector of the dynamic factors and their lags, is a N × qk matrix of dynamic factor loadings, is a qk × qk companion matrix and G is a qk × q selector matrix. The advantage of using the state-space modelling framework is that it can easily and efficiently accommodate unbalanced datasets. See Hartigan and Wright (2023) for more details on the parameters and estimation procedure we use.
2.2.1 Determining the optimal DFM specification
Before we can estimate the DFM we first need to specify four important features. These are: i) the number of dynamic factors ( q ), ii) the number of dynamic loadings ( s ), iii) the lag order for the factor VAR in the state equation ( p ), and iv) the ‘named factor’ necessary for identification.
We use the information criterion developed by Hallin and Liška (2007) to determine the number of dynamic factors. This suggests there is only one common dynamic factor in the targeted predictor dataset (see Figure A4).[31] To set the number of dynamic factor loadings, we follow the strategy implemented in Luciani (2020). This exploits the fact that a dynamic factor model with q factors can be re-cast as a static factor model with r = q (s + 1) static factors as previously mentioned. Practically, we take a balanced subset of the targeted predictor dataset and compare the proportion of explained variation from the first r eigenvalues from the contemporaneous covariance matrix to the proportion of variation from the first q dynamic eigenvalues from the spectral density matrix averaged over a grid of frequencies (see Forni et al (2000) and Brillinger (1981) for more details). The aim here is to find where there is close agreement between these two measures. Examining Table 1 indicates that one dynamic eigenvalue (i.e. q = 1) explains approximately the same amount of variation as three static eigenvalues (i.e. r = 3) and hence suggests s ≈ 2. Further, Luciani (2020) argues that with s = 2 each series in the targeted predictor dataset is capable of loading on the dynamic factor in a time window of three months. This is interesting as this window corresponds to one quarter.
| Eigenvalue | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | ||
| Dynamic ( q ) | 60.0 | 72.5 | 80.8 | 86.8 | 90.6 | 93.6 | 95.9 | 97.6 | 98.9 | 100.0 | |
| Static ( r ) | 38.0 | 55.1 | 62.3 | 67.8 | 72.0 | 76.1 | 79.6 | 82.5 | 85.0 | 87.1 | |
| Notes: Dynamic eigenvalues estimated from the spectral density matrix of a balanced subset of the targeted predictor dataset averaged over a grid of frequencies from to ; static eigenvalues estimated from the contemporaneous correlation matrix of a balanced subset of the targeted predictor dataset. Bold values denote optimal number of factors. | |||||||||||
We can check whether Boivin and Ng (2006)'s suggestion that reducing the sample size can ‘sharpen the factor structure’ by comparing the amount of explained variation from the extended dataset and targeted predictor dataset. Focusing only on the first dynamic eigenvalue, the amount of variation explained in a balanced subset of the extended dataset is about 52 per cent (not shown), lower than the per cent of explained variation in the pre-screened dataset (Table 1). Hence, removing any series considered uninformative in relation to explaining movements in quarterly GDP growth has increased the signal-to-noise ratio of the common dynamic factor.
With only one common factor, the dynamics of the factor follow an AR process instead of a VAR process. To determine the lag order of the AR process we set this to one (i.e. p = 1) based on the AIC.
The final task needed before estimation can take place is identification. To identify the DFM we impose the ‘named factor’ normalisation (Stock and Watson 2016), which associates a factor with a specific variable.[32] In deciding which targeted predictor to make the named factor we put ‘WMI consumer sentiment’ as the first series because this series has the highest Wald statistic of all the 30 targeted predictors (see Figure Al).
2.2.2 Estimation results
Figure 1 presents the (optimal) filtered estimate of the MAI for the sample period: 1978:M2 to 2022:M9.[33] The MAI reveals three periods of relatively weak activity that correspond with previous recessions in Australia, with the most recent being from the COVID-19 crisis (i.e. 1982, 1989-1991 and 2020). Indeed, the decline in the level of the MAI during this period is the largest ever observed in the series. Although the duration was much shorter than compared to the other two time periods and is focused predominately in June 2020.
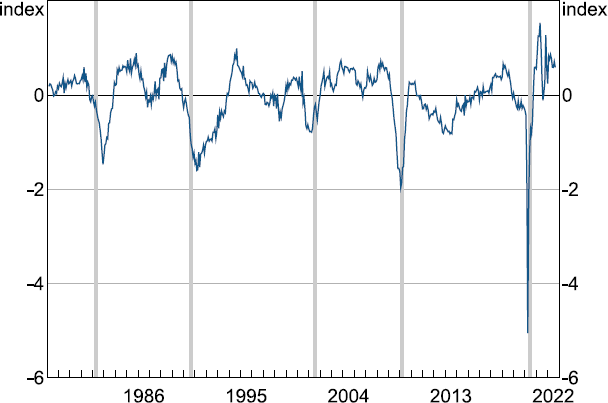
Note: Shaded bars are Sahm rule recession onset dates for Australia, defined as a ¾ percentage point increase in the three-month moving average of the unemployment rate relative to its minimum in the previous twelve months.
The MAI also shows activity was noticeably weak in two other periods which have not previously been considered as recessions as per the technical definition of a recession. The first period, 2001, is linked to the aftereffects of the introduction of the GST which caused a significant amount of activity to be brought forward. The second period, 2008, corresponds with the global financial crisis (GFC). However, both periods together with the three previously acknowledged recessions are detected by the so called ‘Sahm rule’ (Sahm 2019). This is an algorithm for detecting the onset of recessions based on monthly movements in unemployment and has correctly detected every recession in the United States since the 1970s as identified by the NBER, with no false positives.[34] We adjust the Sahm rule for Australia and consider a ¾ percentage point increase in the three-month moving average of the first-release unemployment rate relative to its minimum during the previous twelve months to be more appropriate. With no widely recognised recession timing for Australia equivalent to the NBER Business Cycle Dating Committee for the United States the Sahm rule serves as a useful proxy (see He and Rosewall (2020)). Figure 1 also shows that downturns in the MAI appear to occur several months before detection by the Sahm Rule. In this sense, the MAI provides an important signalling device for policymakers related to probable downturns.
To understand movements in the MAI over time we need to quantify the contributions of individual series. This is something not directly possible to do via non-parametric techniques such as PCA. These contributions are not provided as part of the estimation procedure, but they can be obtained from the state-space representation of the model in Equation (2). First, we take the state equation part of the model and re-write this expression in terms of the updating equation from the Kalman filter:
where Kt is the Kalman Gain at time t and is of dimension r × N and the other parameters are as previously defined. Equation (3) says that the estimate of the common factor at time t is a linear combination of a prediction step (based on information at t–1) and an update step based on the error in the prediction weighted by the Kalman Gain. This second part gives us the contribution from each series to the factor at each time point (see also Sheen et al (2015)).
Next, let Dt denote a r × N matrix of series-specific contributions and using Equation (3) we can get an expression for the update step for each series:[35]
Equation (4) is related to Equation (3) by noting that where is a column vector of 1s with the number of elements specified by m. The first row of Dt for t = 1,...,T gives the individual series-specific contribution to the common dynamic factor ft as defined in Equation (1). Figure 2 plots the contributions to the Kalman filter estimate of the MAI aggregated by data category (i.e. hard, soft or financial) for the period January 2000 until July 2022 to allow for a more easy interpretation of recent history.
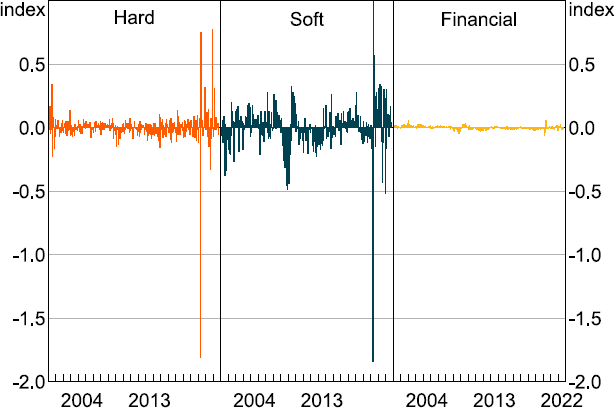
Note: Contribution to state update in Kalman filter recursions.
Figure 2 reveals the soft data category is the main contributor to updates in the MAI followed by hard and financial data. What is interesting about this observation is that the GFC was typically thought of as a financial crisis. However, the break down of the MAI by data category in Figure 2 reveals the previously discussed weakness in the MAI that occurred during the GFC in Australia was primarily due to a decline in soft data and these are mostly sentiment-based series.[36] Financial-based series only contributed a very small amount during that period.
This makes sense because during the GFC the economic environment was very uncertain and there was a lot of pessimism expressed by both consumers and businesses. However, fears of a serious recession turned out to be premature due to a combination of a very large fiscal response by the Australian Government, a very aggressive loosening of monetary policy by the RBA and a surge in demand for commodities from China. The steady rise observed in the MAI until early 2018 was also predominately caused by soft data. More recently, the dramatic movements observed in the MAI during the COVID-19 crisis period were due to contributions from both the hard and soft data categories, with the financial data category only making a relatively minor contribution.
This analysis reveals a potential issue that users of the MAI as a measure of activity need to consider. While soft data, such as surveys, do have the advantage of being very timely compared to hard data categories, they can also provide false signals (Aylmer and Gill 2003). Further, Roberts and Simon (2001) conclude that the information content that survey data, such as sentiment indicators, does provide is at best only a rough summary of prevailing economic conditions. However, they note that in some cases a linear combination of survey indicators (as is the case with a DFM) might not be a bad compromise.
As previously stated, the DFM we use to construct the MAI has been shown to be robust to misspecification including conditional heteroskedasticity and ‘fat tails’ (i.e. outliers) when the factors are extracted from many variables (see Doz et al (2012) and Bańbura et al (2013)). However, it is evident from Figure 1 that the COVID-19 crisis had a substantial effect unlike anything observed before on many of the series included in the targeted predictor dataset. Further, Maroz, Stock and Watson (2021) document how the COVID-19 crisis resulted in a temporarily large change in previously observed patterns of co-movement across a panel of US monthly time series data. While they use a different model than we do, it is still important to check the robustness of our model estimation.
The way we do this in our work is to compare two versions of the MAI constructed using parameters estimated from the full sample (including the COVID-19 crisis, labelled ‘FS’) and parameters estimated up to 2020:M2 (i.e. the pre-COVID-19 crisis, labelled ‘PC’). The results are illustrated in Figure 3 (upper panel) while the difference between the two MAI estimates is displayed in the lower panel. Visually, both MAI estimates look broadly similar. The main difference is that the PC estimate does not fall as dramatically during the worst of the COVID-19 crisis in June 2020. The sample standard deviation of the difference measure for the full sample is 0.15, while the sample standard deviation of the difference measure for the pre-COVID-19 sample is 0.11. The null hypothesis that the sample standard deviation of the full sample difference measure cannot be rejected at standard levels of significance.[37]
One reason for the smaller observed effect in our case compared to the findings of Maroz et al (2021) could be because our dataset does not display the same extreme movements during the COVID-19 crisis as their dataset. Indeed, they report one series having declined by more than 275 standard deviations. In our dataset, the largest decline was much smaller (see Figure A6). Further, given the relatively smaller decline observed in the MAI (PC) during the COVID-19 period, it is reasonable to argue that we need to include the COVID-19 period to ensure we correctly estimate its effect across series and the economy when we turn to nowcasting quarterly GDP growth in the next section.
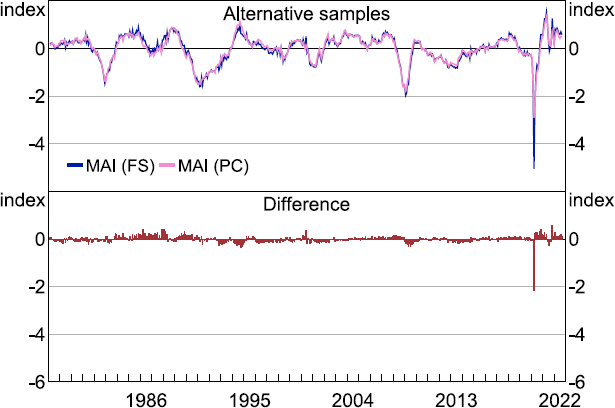
Note: ‘FS’ refers to MAI based on parameters estimated using the full sample; ‘PC’ refers to MAI based on parameters estimated using a sample ending 2020:M2 (i.e. pre-COVID-19).
Footnotes
The reason this is a problem relates to the size of the common component. If too many noisy series are included in the dataset, then the average common component will be smaller than permitted by asymptotic theory. [14]
Bair et al (2006) proposed an idea akin to hard thresholding, calling their procedure ‘supervised principal components’. They follow similar steps to Bai and Ng (2008), but instead of using the t-statistic to decide which series to retain, Bair el al (2006) retain series with coefficient estimates exceeding a threshold in absolute value (with the threshold value determined by cross validation). [15]
See Doz, Giannone and Reichlin (2011, 2012), Bańbura et al (2013) and Bańbura and Modugno (2014). These authors show that the inclusion of disaggregated data does not deteriorate the performance of the DFM. [16]
For example, an important and timely metric of activity is the Labour Force Survey (LFS) which began in February 1978. [17]
Until June quarter 2020, Australia had not experienced a recession (using the technical definition of two consecutive quarters of negative quarterly GDP growth) since the early 1990s. [18]
The alternative method Bai and Ng propose, soft thresholding, is not suitable for our dataset since the algorithms employed to rank series (i.e. LARS, LASSO or the elastic net) require a balanced dataset. [19]
A criticism of hard thresholding suggested by Bulligan et al (2015) is that it tends to select highly collinear predictors. This is because hard thresholding only takes account of the bivariate relationship between the target variable and each predictor in isolation and does not account for the information contained in other predictors. However, it is not really a problem and more likely to be a benefit. Boivin and Ng (2006), Bair et al (2006), Bai and Ng (2008) and Jardet and Meunier (2022) all show that forecast accuracy improves by selecting fewer but more informative predictors. One possible reason for this finding suggested by Boivin and Ng (2006) is that reducing the number of variables can help concentrate the factor structure and enable more efficient estimation. [20]
In all our analyses we work with the compound growth rate of first-release real GDP. [21]
This is the same as the mixed frequency distributed lag model of Koenig et al (2003) and the unrestricted MIDAS model of Foroni et al (2015). [22]
The number of indicator variables were determined by examining individual t-statistics. All but the indicator for 2021:Q1 were significant at the 5 per cent level. [23]
Unlike Bai and Ng (2008), we do not include lags of the dependent variable as additional controls since ACF/PACF plots for quarterly GDP growth suggest there is no statistically significant autocorrelation (see Figure A3). [24]
In comparison, monthly datasets in the United States and Europe typically have hundreds of series to consider. [25]
Using the stricter 5 per cent significance level resulted in 24 series being selected, which we felt was too small as it was at the lower end of the range of 20 to 40 variables suggested by Panagiotelis et al (2019). [26]
The minimum sample size suggested by Bai and Ng (2008) relates to the PCA-based method for estimating factor models. This is not the method we use to estimate the DFM (in Section 2.2). However, our method is identical to both Bańbura et al (2013) and Australian Treasury (2018) and Monte Carlo exercises of Doz et al (2011, 2012) show substantial robustness to misspecification is achieved by this method even with a small number of variables. [27]
A third source of dynamics that is sometimes considered involves allowing the idiosyncratic processes to be autocorrelated. We do not allow for this as the dynamics in the factors will be sufficient to account for the dynamics in the data. [28]
Bai and Wang (2015) regard the specification to be a static factor model when there are no lags in the measurement equation (i.e. s = 0). Luciani (2020) is another example that also implements a DFM with dynamic factor loadings. [29]
Estimation is ‘quasi’-maximum likelihood because the model is misspecified. This comes from assuming that R, the covariance matrix of the idiosyncratic component, is diagonal. Further, we also assume that both noise processes are Gaussian. However, in large samples, this misspecification has been shown to be no issue to consistently estimating the factors and factor loadings (see Doz et al (2012), Bai and Li (2016) and Barigozzi and Luciani (2019)). [30]
The number of dynamic factors is determined by looking for the second ‘region of stability’ in relation to Sc and checking which value of qc this corresponds to. [31]
This is because the likelihood function of our model is invariant to any invertible linear transformation of the factors. That is, for any invertible matrix H the parameters and are observationally equivalent and hence is not identifiable from the data. To achieve identifiability of , we need to impose an identifying restriction. [32]
Three versions of the MAI are available once all the parameters have been estimated using the QMLE procedure. These include the predicted, filtered, and smooth estimates. In our analysis we will only focus on the filtered estimate of the MAI following Sheen et al (2015), who state that the filtered estimate (based on the full sample parameter estimates) is appropriate for conditional forecasting, while the smoothed estimate is appropriate for within-sample estimation. [33]
For the United States, the Sahm rule signals a recession when the three-month moving average of the national unemployment rate rises by a ½ percentage point or more relative to its low during the previous twelve months. [34]
Series from the soft data category are also most correlated with the MAI, as shown by the magnitude of the dynamic loadings for the top ten ranked series in Figure A5. [36]
To test statistical significance, we regress the squared difference series on a constant and compute the t-statistic for the constant term using a long-run variance estimator. The t-statistic is 0.11 while the p-value is 0.91. [37]