RDP 2023-07: Identification and Inference under Narrative Restrictions 4. Identification under NR
October 2023
- Download the Paper 1.10MB
This section formally analyses identification in the SVAR under NR. Section 4.1 considers whether NR are point or set identifying in a frequentist sense. Section 4.2 introduces the notion of a ‘conditional identified set’, which extends the standard notion of an identified set to the setting where the mapping from reduced-form to structural parameters depends on the realisation of the data. This provides an interpretation of the set-valued mapping induced by the NR. Additionally, we make use of the conditional identified set when investigating the frequentist properties of our robust Bayesian procedure in Section 6.
4.1 Point identification under NR
Denoting the true parameter value by , point identification for the parametric model (Equation (24)), which is based on the unconditional likelihood, requires that there is no other parameter value that is observationally equivalent to .[12]
To assess the existence of observationally equivalent parameters, we analyse a statistical distance between and that metrises observational equivalence. Since the support of the distribution of observables can depend on the parameters, it is convenient to work with the Hellinger distance:
and Y is the sample space for YT. As is known in the literature on minimum distance estimation, and are observationally equivalent if and only if or, equivalently, (e.g. Basu, Shioya and Park 2011).
We similarly define the Hellinger distance for the conditional likelihood as
The next proposition analyses the conditions for and , and shows that observational equivalence of and boils down to geometric equivalence of the set of reduced-form VAR innovations satisfying the NR.
Proposition 4.1. Let be the true parameter value and let collect the reduced-form VAR innovations. Define
The unconditional likelihood model (Equation (24)) and the conditional likelihood model (Equation (23)) are globally identified (i.e. there are no observationally equivalent parameter points to ) if and only if is a singleton. If the parameter of interest is an impulse response to the jth structural shock, as defined in Equation (15), then is point identified if the projection of onto its jth column vector is a singleton.
This proposition provides a necessary and sufficient condition for global identification of SVARs by NR. As shown in the proof in Appendix B, defined in this proposition corresponds to the set of observationally equivalent values of Q given , but, importantly, it does not correspond to any flat region of the observed likelihood (the conditional identified set in Definition 4.1 below).
To illustrate this point, consider the bivariate model of Section 2 with the shock-sign restriction (Equation (3)), where yt itself is the reduced-form error, so U in Proposition 4.1 can be set to yk. Given , the set of satisfying the NR is the half-space
The condition for point identification shown in Proposition 4.1 is satisfied if no can generate a half-space identical to Equation (29). Such cannot exist, since a half-space passing through the origin can be indexed uniquely by the slope a1/a2 and Equation (29) implies the slope is a bijective map of on a constrained domain due to the sign normalisation. Figure 3 plots the squared Hellinger distances in the bivariate model under the shock-sign restriction (top panel) and the historical decomposition restriction (bottom panel). For both the conditional and unconditional likelihood, the squared Hellinger distances are minimised uniquely at the true , which is consistent with our point-identification claim for .[13]
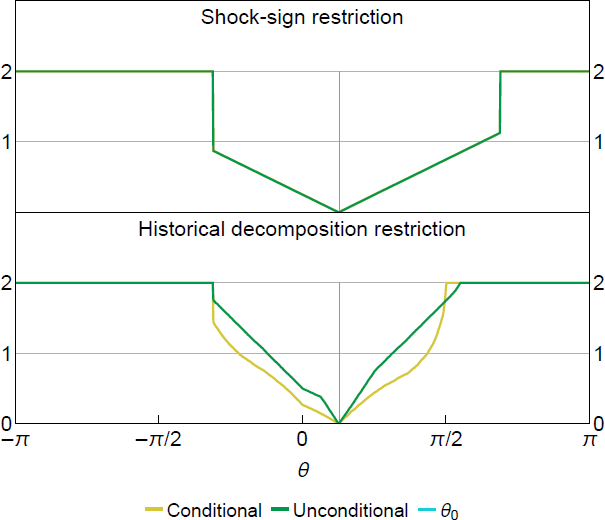
Note: Hellinger distances approximated using Monte Carlo under data-generating processes from Section 2.
Proposition 4.1 also provides conditions under which is not globally identified, but a particular impulse response is. To give an example, consider an SVAR with n > 2 and with a shock-sign restriction on the first shock in period k. Given , the set of satisfying the NR is a half-space defined by . The set of values of uk satisfying this inequality is indexed uniquely by q1 given at its true value, so there are no values of Q that are observationally equivalent to Q0 with . Any value for the remaining n – 1 columns of Q such that they are orthogonal to Q0e1,n will generate the same half-space for uk, so is not a singleton and the SVAR is not globally identified. However, the projection of onto its first column is a singleton, so is globally identified for all i and h.
Although a single NR can deliver global identification in the frequentist sense, the practical implication of this theoretical claim is not obvious. The observed unconditional likelihood is almost always flat at the maximum, so we cannot obtain a unique maximum likelihood estimator for the structural parameter. As a result, the standard asymptotic approximation of the sampling distribution of the maximum likelihood estimator is not applicable. The SVAR model with NR possesses features of set-identified models from the Bayesian standpoint (i.e. flat regions of the likelihood). However, strictly speaking, it can be classified as a globally identified model in the frequentist sense when the condition of Proposition 4.1 holds.
4.2 Conditional identified set
It is well-known that traditional sign restrictions set identify Q or, equivalently, the structural parameters. Given the reduced-form parameters – which are point identified – there are multiple observationally equivalent values of Q, in the sense that there exists Q and such that for every yT in the sample space. The identified set for Q given contains all such observationally equivalent parameter points, and is defined as
The identified set is a set-valued map only of , which carries all the information about Q contained in the data.
The complication in applying this definition of the identified set in SVARs when there are NR is that no longer represents all information about Q contained in the data; by truncating the likelihood, the realisations of the data entering the NR contain additional information about Q. To address this, we introduce a refinement of the definition of an identified set.
Definition 4.1. Let represent a set of NR in terms of the parameters and the data.
(i) The conditional identified set for Q under NR is
The conditional identified set for the impulse response under NR is defined by projecting :
(ii) Let be a statistic. We call s(yT) a sufficient statistic for the conditional identified set if the conditional identified set for Q depends on the sample yT through s(yT); that is, there exists such that
holds for all and .
Unlike the standard identified set , the conditional identified set depends on the sample yT because of the aforementioned data-dependent support of the likelihood. In terms of the observed likelihood, however, they share the property that the likelihood is flat on the (conditional) identified set. Hence, given the sample yT and the reduced-form parameters , all values of Q in fit the data equally well and, in this particular sense, they are observationally equivalent.
When the NR involve shocks in only a subset of time periods (as is typically the case), the conditional identified set depends on the sample only through the observations entering the NR, which are represented by the sufficient statistic s(yT) in Definition 4.1(ii). For instance, in the example of Section 2.1 s(yT) = yk. If we extend the example to the SVAR(p), the shock-sign restriction in Equation (3) is
Hence, the conditional identified set depends on the data only through , so we can set .
If the conditional distribution of YT given s(YT) = s(yT) is non-degenerate, we can consider a frequentist sampling experiment (repeated sampling of YT) conditional on the sufficient statistics set to their observed values. We can then view the conditional identified set as the standard identified set in set-identified models, since it no longer depends on the data in the conditional experiment where s(yT) is fixed. This motivates referring to as the conditional identified set.
The conditional identified set resembles the finite-sample identified set introduced by Rosen and Ura (2020) in the context of maximum score estimation (Manski 1975, 1985). Their set corresponds to the plateau of the population objective function in the conditional frequentist sampling experiment given the regressors. If we impose only the shock-sign restrictions, and given knowledge of the true data-generating processes, the construction of the conditional identified set coincides with the construction of the finite-sample identified set for the scale-normalised coefficients, as they both solve the system of inequalities in Equations (3) or (34).[14] Despite these common geometric features, there are several differences between the SVAR under NR and maximum score estimation. First, the SVAR under NR is a likelihood-based parametric model, while maximum score estimation is a semi-parametric binary regression without a likelihood. Second, NR directly trim the support of the sample objective function (the likelihood) by the intersection of inequalities, while the maximum score objective function counts the number of inequalities satisfied in the sample. Third, the number of NR depends on the researcher's choice, while the number of inequalities in maximum score estimation is driven by the support points of the regressors observed in the sample.
Footnotes
is observationally equivalent to if holds for all yT and . [12]
Under the restriction on the historical decomposition, a notable difference between the conditional and unconditional likelihood cases is the slope of the squared Hellinger distance around the minimum. The squared Hellinger distance of the unconditional likelihood has a steeper slope than the conditional likelihood. This indicates the loss of information for in the conditional likelihood due to conditioning on a non-ancillary event. [13]
See also Komarova (2013) for the construction of identified sets for maximum score coefficients with discrete regressors. [14]