RDP 2023-07: Identification and Inference under Narrative Restrictions 7. Empirical Application: Dynamic Effects of US Monetary Policy
October 2023
- Download the Paper 1.10MB
AR18 estimate the effects of monetary policy on the US economy using a combination of sign restrictions on impulse responses and NR. We explore the degree to which inferences obtained under these restrictions are robust to the choice of conditional prior for Q when using the unconditional likelihood to construct the posterior. We also examine the informativeness of the different NR that are imposed.
The reduced-form VAR is the same as in Uhlig (2005). The model's variables are real GDP, the GDP deflator, a commodity price index, total reserves, non-borrowed reserves (all in natural logarithms) and the federal funds rate; see Arias et al (2019) for details on the variables. The data are monthly from January 1965 to November 2007. The VAR includes a constant and 12 lags.
As NR, AR18 impose that the monetary policy shock in October 1979 was positive and that it was the overwhelming contributor to the unexpected change in the federal funds rate in that month. Following Uhlig (2005), they also impose the sign restrictions that the response of the federal funds rate is non-negative for h = 0, 1,..., 5 and the responses of the GDP deflator, the commodity price index and non-borrowed reserves are non-positive for h = 0, 1,..., 5.
We assume a Jeffreys' (improper) prior over the reduced-form parameters, , which is truncated so that the VAR is stable. The posterior for the reduced-form parameters is then a normal-inverse-Wishart distribution, from which it is straightforward to obtain independent draws (e.g. Del Negro and Schorfheide 2011). We obtain 1,000 draws from the posterior of such that the VAR is stable and is non-empty. To compute sets of posterior means and robust credible intervals, we use Algorithm A.1 in Appendix A, with 1,000 draws of Q used to approximate the bounds of the conditional identified set. If we cannot obtain a draw of Q satisfying the restrictions after 100,000 attempted draws, we approximate as being empty.
Figure 4 presents the impulse responses of the federal funds rate and real GDP to a positive standard deviation monetary policy shock. As a benchmark, we first impose only the sign restrictions on impulse responses (top row). The traditional sign restrictions appear to be fairly uninformative about the output response. The standard Bayesian posterior obtained under a conditionally uniform prior assigns high probability mass to positive output responses (an ‘output puzzle’). The set of posterior means and robust credible intervals also include a wide range of output responses, both positive and negative. This is consistent with the results in Wolf (2020), who shows that linear combinations of expansionary supply and demand shocks may satisfy the sign restrictions and consequently ‘masquerade’ as positive monetary policy shocks.
When additionally imposing the NR based on the October 1979 episode (bottom row), the standard Bayesian posterior concentrates around negative output responses at horizons beyond a year or so. For example, at the two-year horizon and based on the conditionally uniform prior, the posterior probability that the output response is negative is around 80 per cent.[17] At face value, this suggests that the NR based on the October 1979 episode are informative about the effects of monetary policy. However, the set of posterior means and the 68 per cent robust credible intervals include zero at all horizons. This indicates that the inferences about the output response obtained under this set of restrictions are sensitive to the choice of conditional prior. For example, the posterior lower probability – the smallest probability obtainable given the class of posteriors – that the output response is negative at the two-year horizon is only around 10 per cent. The NR based on the October 1979 episode, when combined with the sign restrictions on impulse responses, therefore do not allow us to draw robust conclusions about the sign of the output response to a positive monetary policy shock.
AR18 also consider an alternative set of restrictions based on a richer narrative account of US monetary policy. Specifically, they argue that narrative evidence is consistent with the monetary policy shock being: positive in April 1974, October 1979, December 1988 and February 1994; negative in December 1990, October 1998, April 2001 and November 2002; and the most important contributor to the observed unexpected change in the federal funds rate in these months. Our second exercise examines the informativeness of these restrictions. In particular, we disentangle the informativeness of the shock-sign restrictions from that of the historical decomposition restrictions. The robust Bayesian approach is crucial for carrying out this exercise, since comparisons of standard Bayesian credible intervals across the different sets of restrictions may confound the influence of the conditional prior with the informativeness of the restrictions themselves.
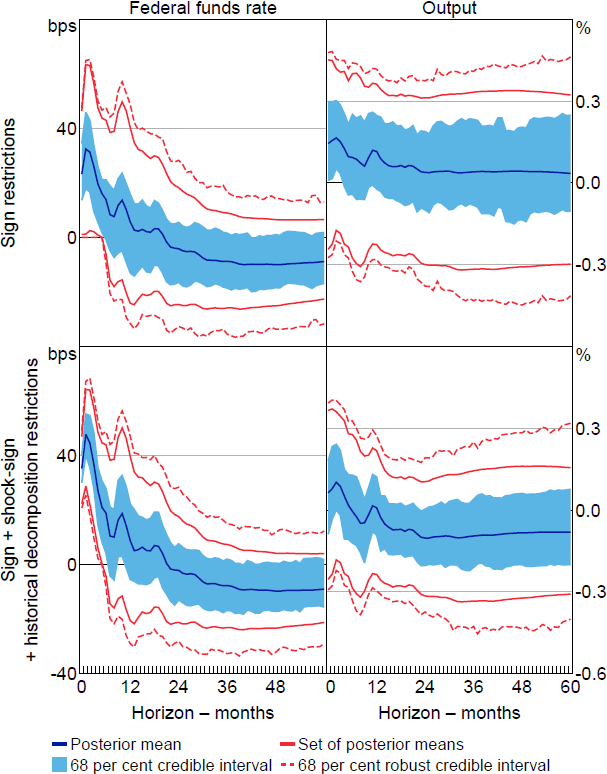
Note: Impulse responses are to a standard deviation shock.
Adding the extended set of shock-sign restrictions to the benchmark sign restrictions narrows the set of posterior means and robust credible intervals (top row of Figure 5), suggesting that these restrictions are somewhat informative. However, the intervals still admit positive output responses at all horizons. Adding the historical decomposition restrictions narrows the sets further (bottom row); for example, the set of posterior means now excludes zero at horizons beyond a year or so. The posterior lower probability that the output response is negative at the two-year horizon is close to 80 per cent, which implies that output falls with high posterior probability regardless of the choice of conditional prior. The extended set of restrictions therefore allows us to draw robust conclusions about the output effects of monetary policy.
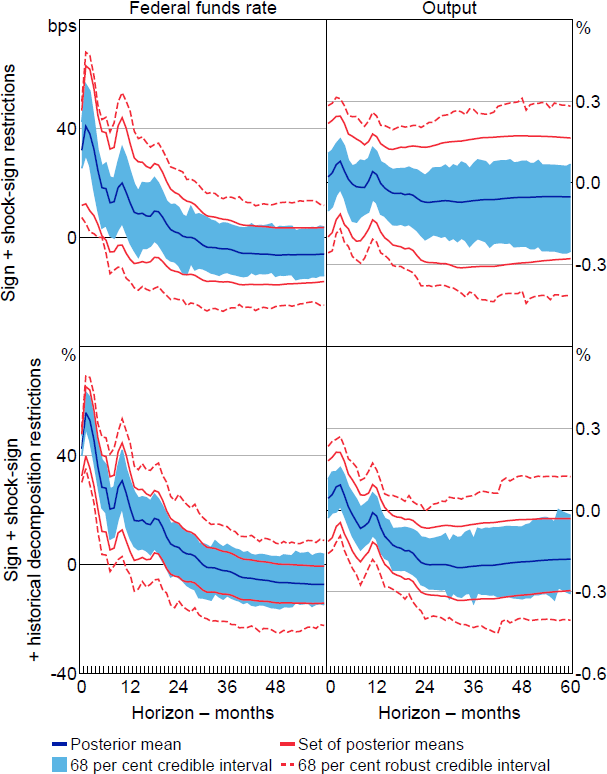
Note: Impulse responses are to a standard deviation shock.
One takeaway from this exercise is that it is necessary to impose NR in at least a handful of periods in order to draw robust conclusions about the effects of US monetary policy; restrictions based on the Volcker episode in isolation are not sufficient. Moreover, much of the apparent information provided by the NR appears to come from the historical decomposition restrictions; the shock-sign restrictions on their own do not allow us to draw robust conclusions.
Footnote
The results are not directly comparable to those in Figure 6 of AR18. First, we present responses to a standard deviation shock, whereas AR18 normalise the median impact response of the federal funds rate to 25 basis points. Second, our prior for Q is conditionally uniform, whereas the prior in AR18 is unconditionally uniform. They also use the conditional likelihood to construct the posterior. [17]