Research Discussion Paper – RDP 2023-07 Identification and Inference under Narrative Restrictions
1. Introduction
Understanding the dynamic causal effects of structural shocks is one of the central problems in macroeconometrics, and there is increasing empirical demand for methods that require minimal identifying assumptions. Replacing point-identifying restrictions in structural vector autoregressions (SVARs) with set-identifying sign restrictions is an early example of this search for robustness (e.g. Uhlig 2005). A more recent example is the idea of substituting or augmenting traditional restrictions on structural parameters with ‘narrative restrictions’ (henceforth NR), which are inequalities involving structural shocks in given time periods (Antolín-Díaz and Rubio-Ramírez (2018) (henceforth AR18); Ludvigson, Ma and Ng (2018)). These restrictions force the SVAR's predictions to be consistent with narratives about the nature of structural shocks driving macroeconomic variation in particular historical episodes. The promise of these restrictions is that they may deliver informative inferences about the effects of structural shocks under weak or uncontroversial restrictions on the structural parameters.
An example of NR are ‘shock-sign restrictions’, such as the restriction in AR18 that the US economy was hit by a positive monetary policy shock in October 1979. This is when the Federal Reserve increased the federal funds rate following Paul Volcker becoming chairman, and is widely considered an example of a positive monetary policy shock (e.g. Romer and Romer 1989). AR18 also consider ‘historical decomposition restrictions’, such as the restriction that the change in the federal funds rate in October 1979 was overwhelmingly due to a monetary policy shock. Other restrictions also fit within this framework, including restrictions on shock magnitudes (e.g. Ludvigson et al 2018) or rankings (e.g. Ben Zeev 2018).
A burgeoning literature imposes NR in a broad range of empirical applications.[1] However, the non-standard nature of these restrictions raises econometric challenges. Under these restrictions, there are no formal results on identification or the validity of frequentist approaches to inference.[2] Moreover, as we show in this paper, the Bayesian procedure of AR18, which is used by the majority of the literature, may be sensitive to prior choice. This paper contributes to the literature by formally analysing identification and inference in models with NR, and by providing an approach to inference that eliminates prior sensitivity. Importantly, this approach is valid from both Bayesian and frequentist perspectives.
From a frequentist perspective, NR are fundamentally different from traditional restrictions. Under normally distributed structural shocks, traditional sign restrictions induce set identification, because they generate a set-valued mapping from the SVAR's reduced-form parameters to its structural parameters – an identified set – that represents observational equivalence. The identified set corresponds to the flat region of the likelihood and, by the definition of observational equivalence, does not depend on the realisation of the data (e.g. Rothenberg 1971). NR also result in the likelihood possessing flat regions and hence generate a set-valued mapping from the reduced-form parameters to the structural parameters. Crucially, this mapping additionally depends on the realisation of the data. The data dependence of this mapping implies that the standard concept of an identified set does not apply. In turn, this means that: 1) existing results on identification in SVARs are inapplicable; and 2) there is no known valid frequentist procedure for inference.
From a Bayesian perspective, the bulk of the empirical literature conducts Bayesian inference under NR in a similar way as under traditional restrictions by following a procedure in AR18. We highlight two issues with the existing approach: the potentially spurious effects on inference of using a conditional likelihood to construct the posterior; and the sensitivity of inference to prior choice due to the likelihood possessing flat regions. The prior sensitivity of the existing Bayesian approach makes it difficult to know whether apparently informative inference obtained in empirical studies (e.g. narrow credible intervals) reflects the informativeness of NR or the choice of prior. Removing the effect of the prior allows us to understand if NR deliver on their promise of offering informative inference under minimal assumptions, in contrast with traditional sign restrictions, which have been shown to provide little information in some settings (e.g. Baumeister and Hamilton 2015; Wolf 2020; Read 2022b).
The paper proceeds in four main steps. First, we formalise the identification problem under NR. Second, we propose using the unconditional likelihood, rather than the conditional likelihood, to construct the posterior. Third, we consider a robust (multiple-prior) Bayesian approach to assess and/or eliminate the posterior sensitivity that remains when using the unconditional likelihood. Finally, we show that the robust Bayesian approach has frequentist validity in large samples.
To the best of our knowledge, this is the first paper to study identification under general NR. Plagborg-Møller and Wolf (2021b) note that shock-sign restrictions could in principle be cast as an external instrument (or ‘narrative proxy’) and used to point identify impulse responses in a local projection. Plagborg-Møller (2022) argues that such an approach possesses several appealing robustness properties relative to the likelihood-based approach of AR18 that we consider here, including that it allows for imperfect narrative information and non-invertibility.[3] Petterson, Seim and Shapiro (2023) derive bounds for a slope parameter in a single equation given restrictions on the magnitude of the residuals, but the setting is non-probabilistic.
We make two main contributions to the understanding of identification under NR. First, we provide a necessary and sufficient condition for global identification of a SVAR under NR and as an example show that this condition is satisfied in a bivariate SVAR with a single shock-sign restriction. This means that, in contrast with traditional sign restrictions, NR may be formally point identifying despite generating a set-valued mapping from reduced-form to structural parameters in any particular sample. This result does not, however, deliver a point estimator, because the observed likelihood is almost always flat at the maximum. Second, we introduce the notion of a ‘conditional identified set’, which extends the standard notion of an identified set to a setting where identification is defined in a repeated sampling experiment conditional on the observations entering the NR. This provides an interpretation for the set-valued mapping induced by the NR as the set of observationally equivalent structural parameters in such a conditional frequentist experiment. We make use of the conditional identified set when analysing the frequentist properties of our procedure.
The fact that NR deliver a set of maximum likelihood estimators is reminiscent of maximum score estimation, where the objective function yields a set of maximisers (Manski 1975, 1985). Our conditional identified set, which fixes the flat regions of the likelihood in the conditional frequentist experiment, shares geometric properties with the finite sample identified set introduced by Rosen and Ura (2020) in the maximum score context; however, their finite sample inference procedure does not apply here.
In terms of inference under NR, our contribution can be viewed from both a Bayesian and a frequentist point of view. Our first message to Bayesian researchers is to base analysis on the unconditional likelihood, rather than the conditional likelihood used by AR18. Conditioning can be problematic because, for some types of NR, a component of the prior is updated only in the direction that makes the NR unlikely to hold ex ante. This is due to conditioning on a non-ancillary event, which results in loss of information.
Our second message to Bayesian researchers is that posterior inference may be sensitive to the choice of prior, because the unconditional likelihood has flat regions under NR (the conditional likelihood also has flat regions under shock-sign restrictions). This sensitivity is a problem that also occurs in set-identified models under traditional restrictions (e.g. Poirier 1998; Baumeister and Hamilton 2015). As advocated for by Giacomini and Kitagawa (2021a) (henceforth GK21), this problem can be solved by adopting a robust (multiple-prior) Bayesian approach. GK21 consider robust Bayesian inference in SVARs under traditional set-identifying restrictions, a setting where – unlike in our case – frequentist inference is also available (e.g. Gafarov et al 2018; Granziera et al 2018). They decompose the prior for structural parameters into a prior for reduced-form parameters, which is revisable, and a conditional prior for structural parameters given reduced-form parameters, which is unrevisable. Considering the set of all conditional priors satisfying the identifying restrictions generates a set of posteriors. This removes the source of posterior sensitivity and makes robust Bayesian and frequentist approaches asymptotically equivalent, reconciling the disagreement between frequentist and Bayesian methods that arises in set-identified models (Moon and Schorfheide 2012).[4]
We explain how this robust Bayesian approach can be adapted to NR. Even if a researcher has a credible prior, we recommend reporting the standard Bayesian posterior (under the unconditional likelihood) together with the robust Bayesian output. This allows researchers to assess the extent to which posterior inference may be driven by prior choice. In the absence of a credible prior, we recommend reporting the robust Bayesian output as an alternative to the standard Bayesian posterior.
This paper's contribution to frequentist inference is to provide the first (to our knowledge) asymptotically valid approach to inference under NR. While other frequentist approaches are in principle possible, one appealing feature of the robust Bayesian approach is its numerical tractability. Proving the frequentist asymptotic validity of the approach is challenging, due to the data-dependent mapping induced by the NR that we discussed above. This means that the results in GK21 about the asymptotic equivalence between Bayesian and frequentist inference are not applicable here. We address these challenges by deriving new results on the asymptotics of robust Bayesian analysis under a fixed number of NR, which we argue is the empirically relevant case given the small number of restrictions typically imposed in the literature. We show that, under regularity conditions, the robust credible region provides asymptotically valid frequentist coverage of the conditional identified set for the impulse response, which also implies correct coverage for the true impulse response.
We illustrate our methods by revisiting the monetary SVAR in AR18. We first examine the robustness of conclusions about the output effects of US monetary policy when NR are imposed based only on the Volcker episode. We find that inferences about the output response are sensitive to prior choice, and the restrictions are largely uninformative in the sense that they admit a wide range of positive and negative output responses. Restrictions based on the Volcker episode in isolation are therefore not sufficient to precisely identify the effects of monetary policy. We then impose an extended set of NR related to multiple episodes, and find robust evidence that output falls following a positive monetary policy shock. Disentangling the informativeness of the different restrictions, the shock-sign restrictions on their own are not particularly informative, and drawing robust conclusions about the output response relies on imposing restrictions on the historical decomposition.
The remainder of the paper is structured as follows. Section 2 highlights the econometric issues that arise when imposing NR using a bivariate example. Section 3 describes the general framework. Section 4 analyses global identification under NR and introduces the concept of a conditional identified set. Section 5 discusses how to conduct standard and robust Bayesian inference under NR. Section 6 explores the frequentist properties of the robust Bayesian approach. Section 7 contains the empirical application and Section 8 concludes. The appendices contain proofs and other supplemental material.
Notation: For the matrix X, vec(X) is the vectorisation of X and vech(X) is the half-vectorisation. ei,n is the ith column of the n × n identity matrix, In. 0n×m is a n × m matrix of zeros. 1 (.) is the indicator function.
2. Bivariate Example
We illustrate the econometric issues that arise when imposing NR in the context of the following bivariate SVAR(0): , for t = 1,…,T, where yt = (y1t, y2t)′ and , with . We abstract from dynamics for ease of exposition, but this is without loss of generality. The orthogonal reduced form of the model reparameterises A0 as , where is the lower-triangular Cholesky factor (with positive diagonal elements) of . We parameterise as
and denote the vector of reduced-form parameters as . Q is an orthonormal matrix in the space of 2×2 orthonormal matrices, (2):
where . This formulation of the model, which follows Baumeister and Hamilton (2015), means that the structural parameters can be expressed as functions of the reduced-form parameters and . Restrictions on the structural parameters and/or functions of the structural shocks can then be interpreted as restricting to some set. In what follows, we discuss properties of this set that are key for analysing identification and inference under NR.
2.1 Shock-sign restrictions
Consider the ‘shock-sign restriction’ that is non-negative for some :
Equation (3) implies that the restricted structural shock can be written as a function . Along with the ‘sign normalisation’ , the shock-sign restriction implies that is restricted to the set
The restriction induces a set-valued mapping from to that depends on the realisation of yk. Giacomini et al (2022a) characterise this mapping in the case where . For example, if , then
where . The direct dependence of this mapping on the realisation of the data implies that the standard notion of an identified set – the set of observationally equivalent structural parameters given the reduced-form parameters – does not apply. Consequently, it is not obvious whether the restrictions are, in fact, set identifying in a formal frequentist sense, nor whether existing frequentist procedures for conducting inference in set-identified models are valid. We analyse identification under these restrictions in Section 4.
When conducting Bayesian inference, AR18 construct the posterior using the conditional likelihood – the likelihood of observing the data conditional on the NR holding. Letting , the conditional likelihood is
The denominator in the first term – the ex ante probability that the NR is satisfied – equals ½, because is standard normal. The conditional likelihood therefore depends on only through the indicator function , which truncates the likelihood, with the truncation points depending on yk. To illustrate, the left panel of Figure 1 plots the conditional likelihood as a function of given two realisations of a data-generating process and fixing to its true value.[5] The conditional likelihood is flat over the interval for satisfying the shock-sign restriction and is zero outside this interval. The support of the non-zero region depends on yk.
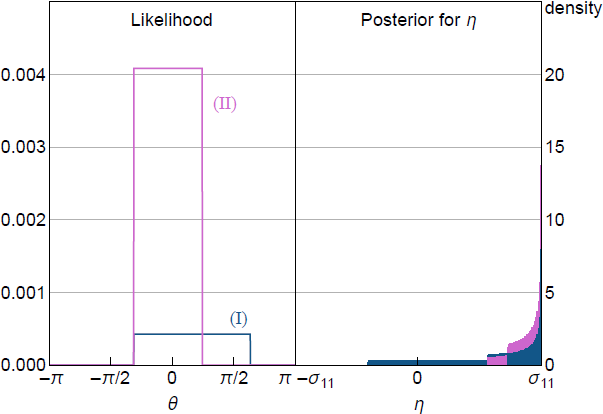
Notes: is known and is the narrative restriction. (I) corresponds to , (II) corresponds to and . Posterior for approximated using 1,000,000 draws of from uniform posterior.
The flat likelihood implies that the posterior for is proportional to the prior in the region where the likelihood is non-zero, and is zero outside this region. The standard approach to Bayesian inference in SVARs under sign restrictions assumes a uniform prior over Q, as do AR18.[6] In the bivariate example, this is equivalent to a prior for that is uniform (Baumeister and Hamilton 2015). This prior implies that the posterior for is also uniform over the interval for where the likelihood is non-zero.
The impact impulse response of y1t to a positive standard deviation shock is . The right panel of Figure 1 plots the posterior for induced by a uniform prior over given the same realisations of the data for which the likelihood was plotted in the left panel. It can be seen that the posterior for assigns more probability mass to more-extreme values of . This highlights that even a uniform prior may be informative for parameters of interest, which also occurs under traditional sign restrictions (Baumeister and Hamilton 2015). One difference is that the prior under sign restrictions is never updated by the data, whereas the support and shape of the posterior for under NR may depend on the realisation of yk through its effect on the truncation points of the likelihood, so there may be some updating of the prior. However, the prior is not updated at values of corresponding to the flat region of the likelihood. Posterior inference about may therefore still be sensitive to the choice of prior, as in standard set-identified SVARs.
2.2 Historical decomposition restrictions
The historical decomposition is the contribution of a particular structural shock to the observed unexpected change in a particular variable over some horizon. The contribution of the first shock to the change in the first variable in the kth period is
while the contribution of the second shock is
Consider the restriction that the first structural shock in period k was positive and (in the language of AR18) the ‘most important contributor’ to the change in the first variable, which requires that . Under these restrictions, must satisfy a set of inequalities that depends on and yk. As in the case of the shock-sign restriction, this set of inequalities generates a set-valued mapping from to that depends on yk.
Let represent the indicator function equal to one when the NR are satisfied and equal to zero otherwise, and let denote the indicator function for the same event in terms of the structural shocks rather than the data. The conditional likelihood given the restrictions is then
In contrast to the case of shock-sign restrictions, the probability in the denominator now depends on through the historical decomposition. Intuitively, changing changes the impulse responses of y1t to the two shocks and thus changes the ex ante probability that . Consequently, the likelihood is not necessarily flat when it is non-zero.
To illustrate, the top panel of Figure 2 plots the conditional likelihood under the historical decomposition NR using the same data-generating process as in Figure 1. The bottom panel plots the probability in the denominator of the conditional likelihood. The likelihood is again truncated, but it is no longer flat – it has a maximum at the value of that minimises the ex ante probability that the NR are satisfied (within the set of values of that are consistent with the restriction given the realisation of the data). The posterior for induced by the usual uniform prior will therefore assign greater posterior probability to values of that yield a lower ex ante probability of satisfying the NR.
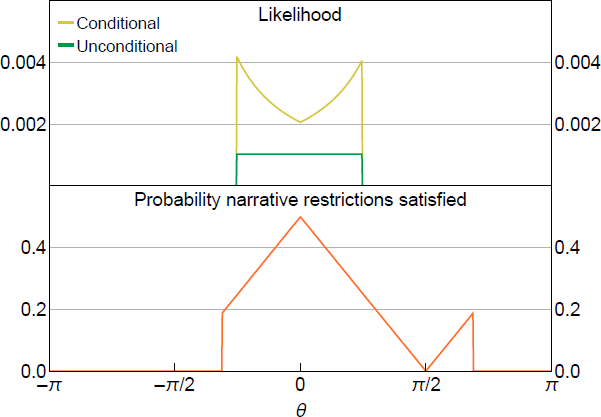
Notes: is known, and and are the narrative restrictions. is approximated using 1,000,000 Monte Carlo draws.
If we view the narrative event () as observable and its probability of occurring depends on the parameter of interest, then conditioning on the narrative event implies that we are conditioning on a non-ancillary statistic. This is undesirable when conducting likelihood-based inference, because it represents a loss of information about the parameter of interest. Unlike for the shock-sign restriction, the probability that the historical decomposition restriction is satisfied depends on , so the event that the NR are satisfied is not ancillary. Conditioning on this event means that the shape of the likelihood (within the non-zero region) is fully driven by the inverse probability of the conditioning event.
Based on this consideration, we therefore advocate constructing the posterior using the joint (or unconditional) likelihood of observing the data and the NR holding:
For all types of NR, the unconditional likelihood is flat with respect to (when it is non-zero) and depends on only through the points of truncation. Of course, this means that posterior inference based on the unconditional likelihood may be sensitive to the choice of prior, as when using the conditional likelihood under shock-sign restrictions. In Section 5.2, we propose how to deal with this posterior sensitivity.
3. General Framework
This section describes the general SVAR, outlines the identifying restrictions we consider, and defines the conditional and unconditional likelihoods in this general setting.
3.1 SVAR
Let yt be an n × 1 vector of variables following the SVAR(p) process:
where: A0 is invertible; with zt containing any exogenous variables (e.g. a constant); ; and are structural shocks. The initial conditions are given.
The reduced-form VAR(p) representation is
where: and with . are the reduced-form parameters.
As is standard in the literature that considers set-identified SVARs, we reparameterise the model into its orthogonal reduced form (e.g. Arias et al 2018):
where: is the lower-triangular Cholesky factor of with non-negative diagonal elements; and Q is an n × n orthonormal matrix with the set of all such matrices. The structural and orthogonal reduced-form parameterisations are related through the mapping and with inverse mapping and
We assume B is such that the VAR(p) can be inverted into an infinite-order vector moving average (VMA) representation:[7]
where Ch is the hth term in and L is the lag operator.[8] The (i, j)th element of the matrix , which we denote by , is the horizon-h impulse response of the ith variable to the jth structural shock:
with the ith row of and qj = Qej,n the jth column of Q.
3.2 Narrative restrictions
In the absence of identifying restrictions, Q – and functions of Q such as – are set identified, since any is consistent with the joint distribution of the data, which is summarised by the reduced-form parameters. Imposing identifying restrictions is equivalent to restricting Q to lie in a subspace of . Throughout, we impose the ‘sign normalisation’ , so a positive value of is a positive shock to the ith equation in the SVAR at time t.
It is common to impose sign restrictions on the impulse responses (e.g. Uhlig 2005) or on the structural parameters (e.g. Arias, Caldara and Rubio-Ramírez 2019). For example, the restriction is a linear inequality restriction on a single column of Q that depends only on the reduced-form parameters . Restrictions on elements of A0 take a similar form.
In contrast, NR constrain the values of the structural shocks in particular periods. The structural shocks are
The shock-sign restriction that the ith structural shock at time k is positive is
We can treat ut as observable given and the data, so we suppress the dependence of ut on and for notational convenience. The restriction in Equation (17) is a linear inequality restriction on a single column of Q. In contrast with traditional sign restrictions, the shock-sign restriction depends directly on the data through the reduced-form VAR innovations.
In addition to shock-sign restrictions, AR18 consider restrictions on the historical decomposition, which is the cumulative contribution of the jth shock to the observed unexpected change in the ith variable between periods k and k+h (i.e. the contribution to the (h+1)-step-ahead forecast error):
An example is the restriction that the jth structural shock was the ‘most important contributor’ to the change in the ith variable between periods k and k + h, which requires that . Another is that the jth structural shock was the ‘overwhelming contributor’ to the change in the ith variable between periods k and k + h, which requires that . From Equation (18), it is clear that these restrictions are nonlinear inequality constraints that simultaneously constrain every column of Q and that depend on the realisations of the data in particular periods in addition to the reduced-form parameters.
Other restrictions also naturally fit within this framework. For instance, Ludvigson et al (2018) restrict the magnitudes of structural shocks in particular periods (e.g. for some specified scalar ). One could also consider restrictions on the relative magnitudes of a particular shock in different periods (e.g. for ).[9]
A collection of NR can be represented in the general form , where s is the number of restrictions. As an illustration, consider the case where there is a single shock-sign restriction in period , as well as the restriction that the first structural shock was the most important contributor to the change in the first variable in period k. Then,
Traditional sign and zero restrictions can also be imposed alongside NR. We follow AR18 by explicitly allowing for sign restrictions on impulse responses and on elements of A0. We denote such sign restrictions by , where is the number of traditional sign restrictions. It is straightforward to additionally allow for zero restrictions, so long as these are not over-identifying. These include ‘short-run’ zero restrictions (Sims 1980), ‘long-run’ zero restrictions (Blanchard and Quah 1989), or restrictions arising from external instruments (Mertens and Ravn 2013; Stock and Watson 2018; Aria, Rubio-Ramírez and Waggoner 2021).[10]
3.3 Conditional and unconditional likelihoods
When constructing the posterior of the SVAR's parameters, AR18 use the likelihood conditional on the NR holding. Define
The likelihood conditional on DN = 1 can be written as
is the joint density of the data given (i.e. the likelihood of the reduced-form VAR), which depends only on and the data. The indicator function equals one when the NR are satisfied and is zero otherwise. This determines the truncation points of the likelihood. is the ex anteprobability that the NR are satisfied. This is constant when there are only shock-sign restrictions; for example, if there are s shock-sign restrictions, . When there are restrictions on the historical decomposition, this probability depends on and Q.
Consider the case where is known, which will be the case asymptotically because is point identified. When depends on Q, the conditional likelihood is maximised at the value of Q that minimises (within the set of values of Q satisfying the restrictions). The posterior based on this likelihood therefore places higher posterior probability on values of Q that result in a lower ex ante probability that the restrictions are satisfied. As discussed in Section 2.2, this is an artefact of conditioning on a non-ancillary event, which represents a loss of information.
We therefore advocate constructing the likelihood without conditioning on the NR holding. The unconditional likelihood (the joint distribution of the data and DN) is
For any value of such that yT is compatible with the NR, there is a set of values of Q that satisfy the restrictions, which depend on the data, but the value of the unconditional likelihood is the same for any Q in this set. The conditional posterior for Q given is therefore proportional to the conditional prior in these regions. Given a fixed number of NR, the likelihood has flat regions even with a time series of infinite length, so posterior inference may be sensitive to the choice of conditional prior for Q given , even asymptotically (which is also the case for the conditional likelihood when the restrictions are ancillary). This motivates considering Bayesian procedures that are robust to the choice of conditional prior, which we explore in Section 5.2.
3.4 Discussion of assumptions
3.4.1 Distributional assumptions
Researchers may be concerned about misspecification with regards to the assumption of standard normal shocks. For instance, one could worry that the periods in which the NR are imposed are ‘unusual’ in the sense that the structural shocks in these periods were drawn from a distribution with, say, different variance or fat tails. The unconditional likelihood depends on the normality assumption only through the reduced-form VAR likelihood, . By omitting terms in corresponding to the periods in which the NR are imposed, one can thus conduct inference that is robust to the distributional assumption about the shocks in these particular periods.
To illustrate, consider the case where NR are imposed in period k only and assume the likelihood for yT takes the form
where
and is an unknown, potentially non-normal, density. Replacing in Equation (24) with yields an ‘unconditional partial likelihood’ that does not depend on the distribution of , but is still truncated by the NR. This would potentially result in a loss of information relative to a likelihood that correctly specifies the distribution of the shocks in period k. However, when NR are imposed in only a few periods, this loss is likely to be small. In contrast, when using the conditional likelihood, the distribution of the structural shocks must be specified in all periods to be able to compute .
Concerns about misspecification may also be alleviated by recognising that the distributional assumption is irrelevant asymptotically. The set of values of Q with non-zero unconditional likelihood depends only on and the realisation of the data in the periods in which the NR are imposed. Under regularity assumptions, the likelihood (and thus the posterior) of will converge to a point at the true value of asymptotically regardless of whether the true data-generating process is a VAR with homoskedastic normal shocks.[11] The set of values of Q with non-zero likelihood will therefore converge asymptotically to the same set regardless of whether the distributional assumption is correct.
3.4.2 Mechanism generating NR
In line with the existing literature, we do not explicitly model the mechanism responsible for revealing the information underlying the NR (i.e. whether DN =1 or DN =0) or the mechanism determining the periods in which this information is revealed (e.g. the identity of k in examples above). If the revelation of this information depends on the data, the likelihood will be misspecified. The exact implications of this misspecification for identification or inference will depend on assumptions about the mechanism revealing the narrative information. Exploring the consequences of such misspecification may be an interesting area for further work. In the bivariate model of Section 2, if the identity of k is randomly determined independently of , we can interpret the current analysis conditional on k.
4. Identification under NR
This section formally analyses identification in the SVAR under NR. Section 4.1 considers whether NR are point or set identifying in a frequentist sense. Section 4.2 introduces the notion of a ‘conditional identified set’, which extends the standard notion of an identified set to the setting where the mapping from reduced-form to structural parameters depends on the realisation of the data. This provides an interpretation of the set-valued mapping induced by the NR. Additionally, we make use of the conditional identified set when investigating the frequentist properties of our robust Bayesian procedure in Section 6.
4.1 Point identification under NR
Denoting the true parameter value by , point identification for the parametric model (Equation (24)), which is based on the unconditional likelihood, requires that there is no other parameter value that is observationally equivalent to .[12]
To assess the existence of observationally equivalent parameters, we analyse a statistical distance between and that metrises observational equivalence. Since the support of the distribution of observables can depend on the parameters, it is convenient to work with the Hellinger distance:
and Y is the sample space for YT. As is known in the literature on minimum distance estimation, and are observationally equivalent if and only if or, equivalently, (e.g. Basu, Shioya and Park 2011).
We similarly define the Hellinger distance for the conditional likelihood as
The next proposition analyses the conditions for and , and shows that observational equivalence of and boils down to geometric equivalence of the set of reduced-form VAR innovations satisfying the NR.
Proposition 4.1. Let be the true parameter value and let collect the reduced-form VAR innovations. Define
The unconditional likelihood model (Equation (24)) and the conditional likelihood model (Equation (23)) are globally identified (i.e. there are no observationally equivalent parameter points to ) if and only if is a singleton. If the parameter of interest is an impulse response to the jth structural shock, as defined in Equation (15), then is point identified if the projection of onto its jth column vector is a singleton.
This proposition provides a necessary and sufficient condition for global identification of SVARs by NR. As shown in the proof in Appendix B, defined in this proposition corresponds to the set of observationally equivalent values of Q given , but, importantly, it does not correspond to any flat region of the observed likelihood (the conditional identified set in Definition 4.1 below).
To illustrate this point, consider the bivariate model of Section 2 with the shock-sign restriction (Equation (3)), where yt itself is the reduced-form error, so U in Proposition 4.1 can be set to yk. Given , the set of satisfying the NR is the half-space
The condition for point identification shown in Proposition 4.1 is satisfied if no can generate a half-space identical to Equation (29). Such cannot exist, since a half-space passing through the origin can be indexed uniquely by the slope a1/a2 and Equation (29) implies the slope is a bijective map of on a constrained domain due to the sign normalisation. Figure 3 plots the squared Hellinger distances in the bivariate model under the shock-sign restriction (top panel) and the historical decomposition restriction (bottom panel). For both the conditional and unconditional likelihood, the squared Hellinger distances are minimised uniquely at the true , which is consistent with our point-identification claim for .[13]
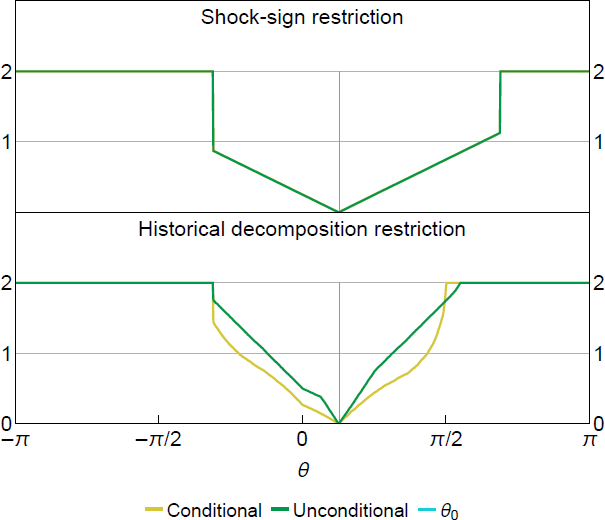
Note: Hellinger distances approximated using Monte Carlo under data-generating processes from Section 2.
Proposition 4.1 also provides conditions under which is not globally identified, but a particular impulse response is. To give an example, consider an SVAR with n > 2 and with a shock-sign restriction on the first shock in period k. Given , the set of satisfying the NR is a half-space defined by . The set of values of uk satisfying this inequality is indexed uniquely by q1 given at its true value, so there are no values of Q that are observationally equivalent to Q0 with . Any value for the remaining n – 1 columns of Q such that they are orthogonal to Q0e1,n will generate the same half-space for uk, so is not a singleton and the SVAR is not globally identified. However, the projection of onto its first column is a singleton, so is globally identified for all i and h.
Although a single NR can deliver global identification in the frequentist sense, the practical implication of this theoretical claim is not obvious. The observed unconditional likelihood is almost always flat at the maximum, so we cannot obtain a unique maximum likelihood estimator for the structural parameter. As a result, the standard asymptotic approximation of the sampling distribution of the maximum likelihood estimator is not applicable. The SVAR model with NR possesses features of set-identified models from the Bayesian standpoint (i.e. flat regions of the likelihood). However, strictly speaking, it can be classified as a globally identified model in the frequentist sense when the condition of Proposition 4.1 holds.
4.2 Conditional identified set
It is well-known that traditional sign restrictions set identify Q or, equivalently, the structural parameters. Given the reduced-form parameters – which are point identified – there are multiple observationally equivalent values of Q, in the sense that there exists Q and such that for every yT in the sample space. The identified set for Q given contains all such observationally equivalent parameter points, and is defined as
The identified set is a set-valued map only of , which carries all the information about Q contained in the data.
The complication in applying this definition of the identified set in SVARs when there are NR is that no longer represents all information about Q contained in the data; by truncating the likelihood, the realisations of the data entering the NR contain additional information about Q. To address this, we introduce a refinement of the definition of an identified set.
Definition 4.1. Let represent a set of NR in terms of the parameters and the data.
(i) The conditional identified set for Q under NR is
The conditional identified set for the impulse response under NR is defined by projecting :
(ii) Let be a statistic. We call s(yT) a sufficient statistic for the conditional identified set if the conditional identified set for Q depends on the sample yT through s(yT); that is, there exists such that
holds for all and .
Unlike the standard identified set , the conditional identified set depends on the sample yT because of the aforementioned data-dependent support of the likelihood. In terms of the observed likelihood, however, they share the property that the likelihood is flat on the (conditional) identified set. Hence, given the sample yT and the reduced-form parameters , all values of Q in fit the data equally well and, in this particular sense, they are observationally equivalent.
When the NR involve shocks in only a subset of time periods (as is typically the case), the conditional identified set depends on the sample only through the observations entering the NR, which are represented by the sufficient statistic s(yT) in Definition 4.1(ii). For instance, in the example of Section 2.1 s(yT) = yk. If we extend the example to the SVAR(p), the shock-sign restriction in Equation (3) is
Hence, the conditional identified set depends on the data only through , so we can set .
If the conditional distribution of YT given s(YT) = s(yT) is non-degenerate, we can consider a frequentist sampling experiment (repeated sampling of YT) conditional on the sufficient statistics set to their observed values. We can then view the conditional identified set as the standard identified set in set-identified models, since it no longer depends on the data in the conditional experiment where s(yT) is fixed. This motivates referring to as the conditional identified set.
The conditional identified set resembles the finite-sample identified set introduced by Rosen and Ura (2020) in the context of maximum score estimation (Manski 1975, 1985). Their set corresponds to the plateau of the population objective function in the conditional frequentist sampling experiment given the regressors. If we impose only the shock-sign restrictions, and given knowledge of the true data-generating processes, the construction of the conditional identified set coincides with the construction of the finite-sample identified set for the scale-normalised coefficients, as they both solve the system of inequalities in Equations (3) or (34).[14] Despite these common geometric features, there are several differences between the SVAR under NR and maximum score estimation. First, the SVAR under NR is a likelihood-based parametric model, while maximum score estimation is a semi-parametric binary regression without a likelihood. Second, NR directly trim the support of the sample objective function (the likelihood) by the intersection of inequalities, while the maximum score objective function counts the number of inequalities satisfied in the sample. Third, the number of NR depends on the researcher's choice, while the number of inequalities in maximum score estimation is driven by the support points of the regressors observed in the sample.
5. Bayesian Inference under NR
This section presents approaches to conducting Bayesian inference in SVARs under NR. Section 5.1 discusses how to modify the standard Bayesian approach in AR18 to use the unconditional likelihood rather than the conditional likelihood. Section 5.2 explains how to conduct robust Bayesian inference under NR, which further addresses the issue of posterior sensitivity due to a flat likelihood.
5.1 Standard Bayesian inference
AR18 propose an algorithm for drawing from the uniform normal-inverse-Wishart posterior of given traditional sign restrictions and NR. This is the posterior induced by a normal-inverse-Wishart prior for and a uniform prior for Q. The algorithm draws from a normal-inverse-Wishart distribution and Q from a uniform distribution over , and checks whether the restrictions are satisfied. If not, the joint draw is discarded and another draw is made. If the restrictions are satisfied, the ex ante probability that the NR are satisfied at the drawn parameter values is approximated via Monte Carlo simulation. Once sufficient draws are obtained satisfying the restrictions, the draws are resampled with replacement using as importance weights the inverse of the probability that the NR are satisfied.[15]
This algorithm can be interpreted as drawing from the posterior based on the unconditional likelihood and then using importance sampling to transform into draws from the posterior based on the conditional likelihood. Drawing from the posterior based on the unconditional likelihood therefore simply requires omitting the importance-sampling step. Constructing the importance weights requires Monte Carlo integration, which can be computationally expensive, particularly when the NR constrain the structural shocks in multiple periods. Omitting the importance-sampling step can therefore ease computational burden.
The algorithm described above places more weight on values of (relative to the notional normal-inverse-Wishart prior) that are more likely to satisfy the restrictions under the uniform distribution over (i.e. values with ‘larger’ conditional identified sets). As discussed in Uhlig (2017), it may instead be preferable to use a prior that is conditionally uniform over the identified set for Q. To draw from the posterior of under the unconditional likelihood given a conditionally uniform prior for Q simply requires obtaining a fixed number of draws of Q at each draw of .
5.2 Robust Bayesian inference
Standard Bayesian inference based on the unconditional likelihood (or based on the conditional likelihood under shock-sign restrictions) is potentially sensitive to the choice of conditional prior for Q given , because the likelihood possesses flat regions. This section explains how to conduct robust Bayesian inference about a scalar-valued function of the structural parameters under NR and traditional sign restrictions. The approach can be viewed as performing global sensitivity analysis to assess whether posterior conclusions are robust to the choice of prior on the flat regions of the likelihood. We assume that the object of interest is an impulse response , but the discussion applies to any other scalar-valued function of the structural parameters.
Let be a prior over the reduced-form parameters , where is the space of reduced-form parameters such that is non-empty. A joint prior for can be written as , where is supported only on . When there are only traditional identifying restrictions, is not updated by the data, because the likelihood is not a function of Q. Posterior inference may therefore be sensitive to the choice of conditional prior, even asymptotically. As discussed above, a similar issue arises under NR. The difference under NR is that is updated by the data through the truncation points of the unconditional likelihood. However, at each value of , the unconditional likelihood is flat over the set of values of Q satisfying the NR. Consequently, the conditional posterior for is proportional to the conditional prior for at each whenever the conditional identified set for Q given is non-empty.
Rather than specifying a single conditional prior for Q, the robust Bayesian approach of GK21 considers the set of all conditional priors for Q that are consistent with the identifying restrictions:
Notice that we cannot impose the NR using a particular conditional prior due to the data-dependent mapping from to Q induced by the NR. However, by considering all possible conditional priors that are consistent with the traditional identifying restrictions, we trace out all possible conditional posteriors for that are consistent with the traditional identifying restrictions and the NR. This is because the NR truncate the unconditional likelihood and the traditional identifying restrictions truncate the prior for , so the posterior for is supported only on values of Q that satisfy both sets of restrictions.
Given a particular prior for and using the unconditional likelihood, the posterior is
The final expression for the posterior makes it clear that any prior for that is consistent with the traditional identifying restrictions is in effect further truncated by the NR (through the likelihood) once the data are realised. Generating this posterior using every prior in the set of conditional priors yields a set of posteriors for :
Marginalising each posterior in this set induces a set of posteriors for . Associated with each of these posteriors are quantities such as the posterior mean, median and other quantiles. For example, as we consider each possible prior within , we can trace out the set of all possible posterior means for . This will always be an interval, so we can summarise this ‘set of posterior means’ by its end points:
where and is the set of values of Q that are consistent with the traditional identifying restrictions and the NR (i.e. the conditional identified set). In contrast, in GK21 the set of posterior means is obtained by finding the infimum and supremum of over and averaging these over . The important difference from GK21 is that the current set of posterior means depends on the data not only through the posterior for but also through the conditional identified set generated by the NR. As a result, in contrast with GK21, we cannot interpret the set of posterior means (Equation (38)) as a consistent estimator for the identified set for (which is not well-defined, as we discussed above). Nevertheless, the set of posterior means still carries a robust Bayesian interpretation similar to GK21 in that it clarifies posterior results that are robust to the choice of prior on the non-updated part of the parameter space (i.e. on the flat regions of the likelihood).
As in GK21, we can also report a robust credible region with credibility level . This is the shortest interval estimate for such that the posterior probability put on the interval is greater than or equal to uniformly over the posteriors in (see Proposition 1 of GK21). We can also report posterior lower and upper probabilities. These are the infimum and supremum, respectively, of the probability for a hypothesis over all posteriors in the set.
To numerically implement this robust Bayesian procedure, we extend the numerical algorithms in GK21 to handle NR. We approximate the bounds of the conditional identified set at each value of using a simulation-based approach based on Algorithm 2 of GK21. See Appendix A for details.
6. Frequentist Coverage
This section analyses the frequentist properties of the robust Bayesian approach under NR. GK21 provide conditions under which the robust credible region is an asymptotically valid confidence set for the true identified set. For the same reason as mentioned above, however, frequentist validity of the robust credible region does not immediately extend to the NR case.
We assume that the number of NR is fixed when the sample size grows, representing situations where the number of NR is ‘small’ relative to the sample size. This setting is empirically relevant given that the literature typically imposes no more than a handful of NR. The sense in which the number of NR is ‘small’ is made precise in the following assumption.
Assumption 1. (Fixed-dimensional s(YT)): The conditional identified set under NR has sufficient statistics s(YT), as defined in Definition 4.1(ii), and the dimension of s(YT) does not depend on T.
Let be the true parameter values. We view the sample YT as being drawn from . Let be the conditional distribution of the sample YT given the sufficient statistics for the conditional identified set s = s(YT) at . We denote by the distribution of the sufficient statistics s(YT) at . The next assumption assumes that in the conditional sampling experiment given s(YT), the sampling distribution for the maximum likelihood estimator centered at and the posterior for centered at asymptotically coincide. To characterise the asymptotic properties of our inference proposals, let be a sequence of endogenous variables of infinite length, (yt : t = 1,2,...), generated according to the SVAR(p) model of Equation (11). We denote its true probability law as P0, whose marginal distribution for the first T realisations, YT, corresponds to .
Assumption 2. (Conditional Bernstein-von Mises property for ): For -almost every s and -almost every sampling sequence , the posterior for asymptotically coincides with the sampling distribution of under as , in the sense stated in Assumption 5(i) in GK21.
This is a key assumption for establishing the asymptotic frequentist validity of the robust credible region under NR. It holds, for instance, when s(yT) corresponds to one or a few observations in the whole sample, as we had in the example of Section 2.1. In this case, the influence of s(yT) vanishes in the conditional sampling distribution of as , as the latter asymptotically agrees with the asymptotically normal sampling distribution for the maximum likelihood estimator with variance-covariance matrix given by the inverse of the Fisher information matrix. By the well-known Bernstein-von Mises theorem for regular parametric models, the posterior for asymptotically agrees with this sampling distribution.
The last assumption requires convexity and smoothness of the conditional identified set, and is analogous to Assumption 5(ii) of GK21 for set-identified models.
Assumption 3. (Almost-sure convexity and smoothness of the impulse response identified set): Let be the conditional identified set for with the sufficient statistics s(YT). For any T and -almost every is closed and convex, , and its lower and upper bounds are differentiable in at with non-zero derivatives.
Propositions B.1-B.3 provide primitive conditions for Assumption 3 to hold in the case where there are shock-sign restrictions. Imposing Assumptions 1, 2 and 3, we obtain the following theorem characterising the asymptotic frequentist properties of the robust credible interval under NR.
Theorem 6.1. For , let be the volume-minimising robust credible region for with credibility , [16] which satisfies
Under Assumptions 1, 2, and 3, attains asymptotically valid coverage for the true impulse response, , conditional on s(YT):
Accordingly, attains asymptotically valid coverage for unconditionally,
This theorem shows that the robust credible region applied to the SVAR model with NR attains asymptotically valid frequentist coverage for the impulse response conditional identified set and consequently for the true impulse response. Even if the point-identification condition of Proposition 4.1 holds for the impulse response, it is not obvious that the standard (single prior) Bayesian credible region can attain frequentist coverage. This is because the Bernstein-von Mises theorem does not seem to hold for the impulse response due to the non-standard features of models with NR.
7. Empirical Application: Dynamic Effects of US Monetary Policy
AR18 estimate the effects of monetary policy on the US economy using a combination of sign restrictions on impulse responses and NR. We explore the degree to which inferences obtained under these restrictions are robust to the choice of conditional prior for Q when using the unconditional likelihood to construct the posterior. We also examine the informativeness of the different NR that are imposed.
The reduced-form VAR is the same as in Uhlig (2005). The model's variables are real GDP, the GDP deflator, a commodity price index, total reserves, non-borrowed reserves (all in natural logarithms) and the federal funds rate; see Arias et al (2019) for details on the variables. The data are monthly from January 1965 to November 2007. The VAR includes a constant and 12 lags.
As NR, AR18 impose that the monetary policy shock in October 1979 was positive and that it was the overwhelming contributor to the unexpected change in the federal funds rate in that month. Following Uhlig (2005), they also impose the sign restrictions that the response of the federal funds rate is non-negative for h = 0, 1,..., 5 and the responses of the GDP deflator, the commodity price index and non-borrowed reserves are non-positive for h = 0, 1,..., 5.
We assume a Jeffreys' (improper) prior over the reduced-form parameters, , which is truncated so that the VAR is stable. The posterior for the reduced-form parameters is then a normal-inverse-Wishart distribution, from which it is straightforward to obtain independent draws (e.g. Del Negro and Schorfheide 2011). We obtain 1,000 draws from the posterior of such that the VAR is stable and is non-empty. To compute sets of posterior means and robust credible intervals, we use Algorithm A.1 in Appendix A, with 1,000 draws of Q used to approximate the bounds of the conditional identified set. If we cannot obtain a draw of Q satisfying the restrictions after 100,000 attempted draws, we approximate as being empty.
Figure 4 presents the impulse responses of the federal funds rate and real GDP to a positive standard deviation monetary policy shock. As a benchmark, we first impose only the sign restrictions on impulse responses (top row). The traditional sign restrictions appear to be fairly uninformative about the output response. The standard Bayesian posterior obtained under a conditionally uniform prior assigns high probability mass to positive output responses (an ‘output puzzle’). The set of posterior means and robust credible intervals also include a wide range of output responses, both positive and negative. This is consistent with the results in Wolf (2020), who shows that linear combinations of expansionary supply and demand shocks may satisfy the sign restrictions and consequently ‘masquerade’ as positive monetary policy shocks.
When additionally imposing the NR based on the October 1979 episode (bottom row), the standard Bayesian posterior concentrates around negative output responses at horizons beyond a year or so. For example, at the two-year horizon and based on the conditionally uniform prior, the posterior probability that the output response is negative is around 80 per cent.[17] At face value, this suggests that the NR based on the October 1979 episode are informative about the effects of monetary policy. However, the set of posterior means and the 68 per cent robust credible intervals include zero at all horizons. This indicates that the inferences about the output response obtained under this set of restrictions are sensitive to the choice of conditional prior. For example, the posterior lower probability – the smallest probability obtainable given the class of posteriors – that the output response is negative at the two-year horizon is only around 10 per cent. The NR based on the October 1979 episode, when combined with the sign restrictions on impulse responses, therefore do not allow us to draw robust conclusions about the sign of the output response to a positive monetary policy shock.
AR18 also consider an alternative set of restrictions based on a richer narrative account of US monetary policy. Specifically, they argue that narrative evidence is consistent with the monetary policy shock being: positive in April 1974, October 1979, December 1988 and February 1994; negative in December 1990, October 1998, April 2001 and November 2002; and the most important contributor to the observed unexpected change in the federal funds rate in these months. Our second exercise examines the informativeness of these restrictions. In particular, we disentangle the informativeness of the shock-sign restrictions from that of the historical decomposition restrictions. The robust Bayesian approach is crucial for carrying out this exercise, since comparisons of standard Bayesian credible intervals across the different sets of restrictions may confound the influence of the conditional prior with the informativeness of the restrictions themselves.
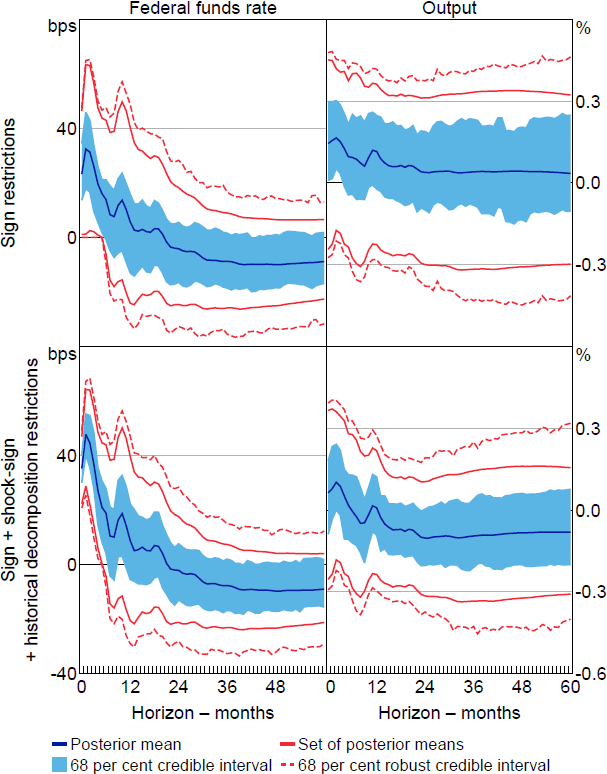
Note: Impulse responses are to a standard deviation shock.
Adding the extended set of shock-sign restrictions to the benchmark sign restrictions narrows the set of posterior means and robust credible intervals (top row of Figure 5), suggesting that these restrictions are somewhat informative. However, the intervals still admit positive output responses at all horizons. Adding the historical decomposition restrictions narrows the sets further (bottom row); for example, the set of posterior means now excludes zero at horizons beyond a year or so. The posterior lower probability that the output response is negative at the two-year horizon is close to 80 per cent, which implies that output falls with high posterior probability regardless of the choice of conditional prior. The extended set of restrictions therefore allows us to draw robust conclusions about the output effects of monetary policy.
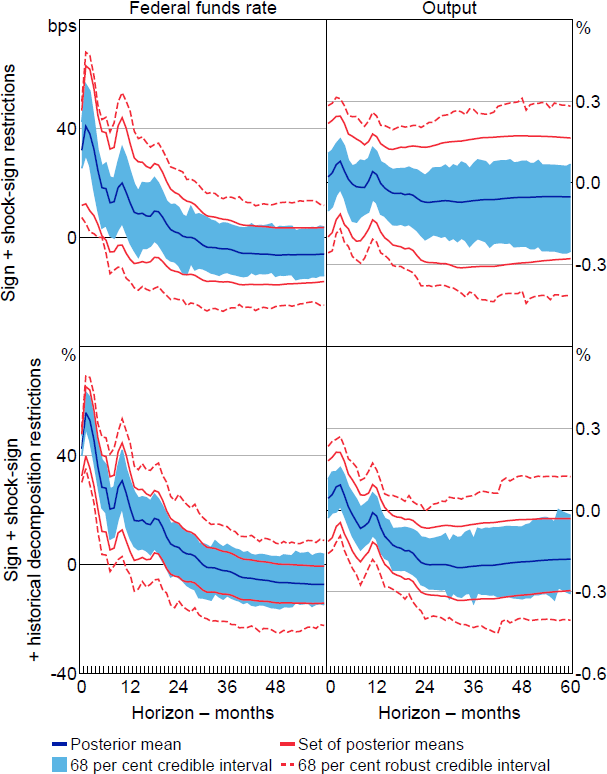
Note: Impulse responses are to a standard deviation shock.
One takeaway from this exercise is that it is necessary to impose NR in at least a handful of periods in order to draw robust conclusions about the effects of US monetary policy; restrictions based on the Volcker episode in isolation are not sufficient. Moreover, much of the apparent information provided by the NR appears to come from the historical decomposition restrictions; the shock-sign restrictions on their own do not allow us to draw robust conclusions.
8. Conclusion
Restricting the values of structural shocks to be consistent with historical narratives offers a potentially useful approach to learning about the effects of structural shocks in SVARs, but raises novel issues related to identification and inference. We study such issues and propose a method for conducting inference that is valid from both Bayesian and frequentist points of view.
Using our method, we assess whether conclusions about the effects of US monetary policy obtained under narrative restrictions are robust to the choice of prior. We find that restrictions based on the Volcker episode in isolation are not sufficiently informative to draw robust conclusions about the output effects of monetary policy. However, under a richer set of restrictions, there is robust evidence that output falls following a positive monetary policy shock.
While we focus on SVARs, our analysis could be extended to other settings. For example, Plagborg-Møller and Wolf (2021a) explain how to impose traditional SVAR identifying restrictions in the local projection framework under the assumption that the structural shocks are invertible. In this context it should also be possible to impose narrative restrictions and to conduct inference using robust Bayesian methods, but we leave this analysis to future research.
Appendix A: Numerical Implementation
This appendix describes a general algorithm to implement the robust Bayesian procedure under NR. GK21 propose numerical algorithms for conducting robust Bayesian inference in SVARs identified using traditional sign and zero restrictions. Their Algorithm 1 uses a numerical optimisation routine to obtain the lower and upper bounds of the identified set at each draw of . Obtaining the bounds via numerical optimisation may be difficult under the set of NR considered here, since the problem is non-convex. We therefore adapt Algorithm 2 of GK21, which approximates the bounds of the identified set at each draw of using Monte Carlo simulation.
Algorithm A.1. Let be the set of NR and let be the set of traditional sign restrictions (excluding the sign normalisation). Assume the object of interest is
- Step 1: Specify a prior for and obtain the posterior .
- Step 2: Draw from and check whether is empty using the subroutine below.
- Step 2.1: Draw an n × n matrix of independent standard normal random variables, Z, and let be the QR decomposition of Z.[18]
Step 2.2: Define
where is the jth column of .
- Step 2.3: Check whether Q satisfies and . If so, retain Q and proceed to Step 3. Otherwise, repeat Steps 2.1 and 2.2 (up to a maximum of L times) until Q is obtained satisfying the restrictions. If no draws of Q satisfy the restrictions, approximate as being empty and return to Step 2.
- Step 3: Repeat Steps 2.1–2.3 until K draws of Q are obtained. Let be the K draws of Q that satisfy the restrictions and let qj,k be the jth column of Qk. Approximate by .
- Step 4: Repeat Steps 2–3 M times to obtain for m = 1, ...,M. Approximate the set of posterior means using the sample averages of and .
- Step 5: To obtain an approximation of the smallest robust credible region with credibility define and let be the sample quantile of . An approximated smallest robust credible interval for is an interval centered at with radius .
Algorithm 1 approximates at each draw of via Monte Carlo simulation. The approximated set will be too narrow given a finite number of draws of Q, but the approximation error will vanish as the number of draws goes to infinity. Montiel Olea and Nesbit (2021) derive bounds on the number of draws required to control approximation error.
The algorithm may be computationally demanding when the restrictions substantially truncate , because many draws of Q may be rejected at each draw of .[19] However, the same draws of Q can be used to compute and for different objects of interest, which cuts down on computation time. For example, the same draws can be used to compute the impulse responses of all variables to all shocks at all horizons of interest. Other quantities of interest can also be computed, such as impulse responses to ‘unit’ shocks (e.g. Read 2022b), forecast error variance decompositions, elements of A0 or A+, historical decompositions or structural shocks.
Appendix B: Proofs
Proof of Proposition 4.1. can be written as
The likelihood for the reduced-form parameters point identifies , so holds only at . Hence, we set and consider ,
if and only if holds almost surely under . In terms of the reduced-form residuals entering the NR, the latter condition is equivalent to up to a null set under . Hence, defined in the proposition collects observationally equivalent values of Q at in terms of the unconditional likelihood.
Next, for the case of the the conditional likelihood, consider
where the inequality follows from the Cauchy-Schwartz inequality. The inequality is satisfied with equality if and only if holds almost surely under . Hence, by repeating the argument for the unconditional likelihood case, we conclude that consists of observationally equivalent values of Q at in terms of the conditional likelihood.
Proof of Theorem 6.1. Since satisfies the imposed NR and the other sign restrictions (if any imposed), holds for any yT. Hence, for all T,
To prove the claim, it suffices to focus on the asymptotic behaviour of the coverage probability for the conditional identified set shown in the right-hand side.
Under Assumptions 2 and 3, the asymptotically correct coverage for the conditional identified set can be obtained by applying Proposition 2 in GK21.
B.1 Primitive Conditions for Assumption 3.
In what follows, we present sufficient conditions for convexity, continuity and differentiability (both in ) of the conditional impulse response identified set under the assumption that there is a fixed number of shock-sign restrictions constraining the first structural shock only (possibly in multiple periods).[20]
Proposition B.1. (Convexity) Let the parameter of interest be . Assume that there are shock-sign restrictions on for t = t1,...,tK, so Then the set of values of satisfying the shock-sign restrictions and sign normalisation, is convex for all i and h if there exists a unit-length vector satisfying
Proof. If there exists a unit-length vector q satisfying the inequality in Equation (B2), it must lie within the intersection of the K half-spaces defined by the inequalities the half-space defined by the sign normalisation, , and the unit sphere in . The intersection of these K+1 half-spaces and the unit sphere is a path-connected set. Since is a continuous function of q1, the set of values of satisfying the restrictions is an interval and is thus convex, because the set of a continuous function with a path-connected domain is always an interval.
Proposition B.2. (Continuity) Let the parameter of interest and restrictions be as in Proposition B.1, and assume that the conditions in the proposition are satisfied. If there exists a unit-length vector such that, at
then and are continuous at for all i and h.[21]
Proof. YT enters the NR through the reduced-form VAR innovations, ut. After noting that the reduced-form VAR innovations are (implicitly) continuous in , continuity of and follows by the same logic as in the proof of Proposition B.2 of Giacomini and Kitagawa (2021b). We omit the detail for brevity.
Proposition B.3. (Differentiability) Let the parameter of interest and restrictions be as in Proposition B.1, and assume that the conditions in the proposition are satisfied. Denote the unit sphere in by If, at , the set of solutions to the optimisation problem
is singleton, the optimised value is non-zero, and the number of binding inequality restrictions at the optimum is at most n – 1, then is almost surely differentiable at .
Proof. One-to-one differentiable reparameterisation of the optimisation problem in Equation (B4) using yields the optimisation problem in Equation (2.5) of Gafarov et al (2018), with a set of inequality restrictions that are a function of the data through the reduced-form VAR innovations entering the NR. Noting that ut is (implicitly) differentiable in , differentiability of at follows from their Theorem 2 under the assumptions that, at , the set of solutions to the optimisation problem is singleton, the optimised value is non-zero, and the number of binding sign restrictions at the optimum is at most n – 1. Differentiability of follows similarly. Note that Theorem 2 of Gafarov et al (2018), when applied to the current context, additionally requires that the column vectors of are linearly independent, but this occurs almost surely under the probability law for YT
References
Altavilla C, M Darracq Pariès and G Nicoletti (2019), ‘Loan Supply, Credit Markets and the Euro Area Financial Crisis’, Journal of Banking & Finance, 109, Article 105658.
Antolín-Díaz J, I Petrella and JF Rubio-Ramírez (2021), ‘Structural Scenario Analysis with SVARs’, Journal of Monetary Economics, 117, pp 798–815.
Antolín-Díaz J and JF Rubio-Ramírez (2018), ‘Narrative Sign Restrictions for SVARs’, The American Economic Review, 108(10), pp 2802–2829.
Arias JE, D Caldara and JF Rubio-Ramírez (2019), ‘The Systematic Component of Monetary Policy in SVARs: An Agnostic Identification Procedure’, Journal of Monetary Economics, 101, pp 1–13.
Arias JE, JF Rubio-Ramírez and DF Waggoner (2018), ‘Inference Based on Structural Vector Autoregressions Identified with Sign and Zero Restrictions: Theory and Applications’, Econometrica, 86(2), pp 685–720.
Arias JE, JF Rubio-Ramírez and DF Waggoner (2021), ‘Inference in Bayesian Proxy-SVARs’, Journal of Econometrics, 225(1), pp 88–106.
Ascari G, S Fasani, J Grazzini and L Rossi (forthcoming), ‘Endogenous Uncertainty and the Macroeconomic Impact of Shocks to Inflation Expectations’, Journal of Monetary Economics.
Badinger H and S Schiman (2023), ‘Measuring Monetary Policy in the Euro Area Using SVARs with Residual Restrictions’, American Economic Journal: Macroeconomics, 15(2), pp 279–305.
Basu A, H Shioya and C Park (2011), Statistical Inference: The Minimum Distance Approach, Monographs on Statistics and Applied Probability 120, Chapman & Hall/CRC Press, Boca Raton.
Baumeister C and JD Hamilton (2015), ‘Sign Restrictions, Structural Vector Autoregressions, and Useful Prior Information’, Econometrica, 83(5), pp 1963–1999.
Ben Zeev N (2018), ‘What Can We Learn about News Shocks from the Late 1990s and Early 2000s Boom-Bust Period?’, Journal of Economic Dynamics & Control, 87, pp 94–105.
Berger T, J Richter and B Wong (2022), ‘A Unified Approach for Jointly Estimating the Business and Financial Cycle, and the Role of Financial Factors’, Journal of Economic Dynamics & Control, 136, Article 104315.
Berthold B (2023), ‘The Macroeconomic Effects of Uncertainty and Risk Aversion Shocks’, European Economic Review, 154, Article 104442.
Blanchard OJ and D Quah (1989), ‘The Dynamic Effects of Aggregate Demand and Supply Disturbances’, The American Economic Review, 79(4), pp 655–673.
Boer L, A Pescatori and M Stuermer (forthcoming), ‘Energy Transition Metals: Bottleneck for Net-Zero Emissions?’, Journal of the European Economic Association.
Caggiano G and E Castelnuovo (2023), ‘Global Financial Uncertainty’, Journal of Applied Econometrics, 38(3), pp 432–449.
Caggiano G, E Castelnuovo, S Delrio and R Kima (2021), ‘Financial Uncertainty and Real Activity: The Good, the Bad, and the Ugly’, European Economic Review, 136, Article 103750.
Cheng K and Y Yang (2020), ‘Revisiting the Effects of Monetary Policy Shocks: Evidence from SVAR with Narrative Sign Restrictions’, Economics Letters, 196, Article 109598.
Conti AM, A Nobili and FM Signoretti (2023), ‘Bank Capital Requirement Shocks: A Narrative Perspective’, European Economic Review, 151, Article 104254.
Del Negro M and F Schorfheide (2011), ‘Bayesian Macroeconometrics’, in J Geweke, G Koop and H van Dijk (eds), The Oxford Handbook of Bayesian Econometrics, Oxford Handbooks, Oxford University Press, Oxford, pp 293–389.
Fanelli L and A Marsi (2022), ‘Sovereign Spreads and Unconventional Monetary Policy in the Euro Area: A Tale of Three Shocks’, European Economic Review, 150, Article 104281.
Furlanetto F and Ø Robstad (2019), ‘Immigration and the Macroeconomy: Some New Empirical Evidence’, Review of Economic Dynamics, 34, pp 1–19.
Gafarov B, M Meier and JL Montiel Olea (2018), ‘Delta-Method Inference for a Class of Set-Identified SVARs’, Journal of Econometrics, 203(2), pp 316–327.
Giacomini R and T Kitagawa (2021a), ‘Robust Bayesian Inference for Set-identified Models’, Econometrica, 89(4), pp 1519–1556.
Giacomini R and T Kitagawa (2021b), ‘Supplement to “Robust Bayesian Inference for Set-Identified Models”’, Econometrica, 89(4), Supporting Information, Online Appendix.
Giacomini R, T Kitagawa and M Read (2021), ‘Robust Bayesian Analysis for Econometrics’, Centre for Economic Policy Research Research Discussion Paper No DP16488.
Giacomini R, T Kitagawa and M Read (2022a), ‘Narrative Restrictions and Proxies’, Journal of Business & Economic Statistics, 40(4), pp 1415–1425.
Giacomini R, T Kitagawa and M Read (2022b), ‘Robust Bayesian Inference in Proxy SVARs’, Journal of Econometrics, 228(1), pp 107–126.
Granziera E, HR Moon and F Schorfheide (2018), ‘Inference for VARs Identified with Sign Restrictions’, Quantitative Economics, 9(3), pp 1087–1121.
Hamilton JD (1994), Time Series Analysis, Princeton University Press, Princeton.
Harrison A, X Liu and SL Stewart (2023), ‘Structural Sources of Oil Market Volatility and Correlation Dynamics’, Energy Economics, 121, Article 106658.
Herwatz H and S Wang (2023), ‘Point Estimation in Sign-Restricted SVARs Based on Independence Criteria with an Application to Rational Bubbles’, Journal of Economic Dynamics & Control, 151, Article 104630.
Inoue A and L Kilian (2022), ‘Joint Bayesian Inference about Impulse Responses in VAR Models’, Journal of Econometrics, 231(2), pp 457–476.
Kilian L and H Lütkepohl (2017), Structural Vector Autoregressive Analysis, Themes in Modern Econometrics, Cambridge University Press, Cambridge.
Kilian L and X Zhou (2020), ‘Does Drawing down the US Strategic Petroleum Reserve Help Stabilize Oil Prices?’, Journal of Applied Econometrics, 35(6), pp 673–691.
Kilian L and X Zhou (2022), ‘Oil Prices, Exchange Rates and Interest Rates’, Journal of International Money and Finance, 126, Article 102679.
Komarova T (2013), ‘Binary Choice Models with Discrete Regressors: Identification and Misspecification’, Journal of Econometrics, 177(1), pp 14–33.
Larsen VH (2021), ‘Components of Uncertainty’, International Economic Review, 62(2), pp 769–788.
Laumer S (2020), ‘Government Spending and Heterogeneous Consumption Dynamics’, Journal of Economic Dynamics & Control, 114, Article 103868.
Ludvigson SC, S Ma and S Ng (2018), ‘Shock Restricted Structural Vector-Autoregressions’, NBER Working Paper No 23225, rev January 2020.
Ludvigson SC, S Ma and S Ng (2021), ‘Uncertainty and Business Cycles: Exogenous Impulse or Endogenous Response?’, American Economic Journal: Macroeconomics, 13(4), pp 369–410.
Maffei-Faccioli N and E Vella (2021), ‘Does Immigration Grow the Pie? Asymmetric Evidence from Germany’, European Economic Review, 138, Article 103846.
Manski CF (1975), ‘Maximum Score Estimation of the Stochastic Utility Model of Choice’, Journal of Econometrics, 3(3), pp 205–228.
Manski CF (1985), ‘Semiparametric Analysis of Discrete Response: Asymptotic Properties of the Maximum Score Estimator’, Journal of Econometrics, 27(3), pp 313–333.
Mertens K and MO Ravn (2013), ‘The Dynamic Effects of Personal and Corporate Income Tax Changes in the United States’, The American Economic Review, 103(4), pp 1212–1247.
Montiel Olea JL and J Nesbit (2021), ‘(Machine) Learning Parameter Regions’, Journal of Econometrics, 221(1, Part C), pp 716–744.
Montiel Olea JL, JH Stock and MW Watson (2021), ‘Inference in Structural Vector Autoregressions Identified with an External Instrument’, Journalof Econometrics, 225(1), pp 74–87.
Moon HR and F Schorfheide (2012), ‘Bayesian and Frequentist Inference in Partially Identified Models’, Econometrica, 80(2), pp 755–782.
Neri S (2023), ‘Long-Term Inflation Expectations and Monetary Policy in the Euro Area before the Pandemic’, European Economic Review, 154, Article 104426.
Petterson MS, D Seim and JM Shapiro (2023), ‘Bounds on a Slope from Size Restrictions on Economic Shocks’, American Economic Journal: Microeconomics, 15(3), pp 552–572.
Plagborg-Møller M (2019), ‘Bayesian Inference on Structural Impulse Response Functions’, Quantitative Economics, 10(1), pp 145–184.
Plagborg-Møller M (2022), ‘Discussion of “Narrative Restrictions and Proxies” by Raffaella Giacomini, Toru Kitagawa, and Matthew Read’, Journal of Business & Economic Statistics, 40(4), pp 1434–1437.
Plagborg-Møller M and CK Wolf (2021a), ‘Local Projections and VARs Estimate the Same Impulse Responses’, Econometrica, 89(2), pp 955–980.
Plagborg-Møller M and CK Wolf (2021b), ‘Supplement to “Local Projections and VARs Estimate the Same Impulse Responses”’, Econometrica, 89(2), Supporting Information, Online Appendix.
Poirier DJ (1998), ‘Revising Beliefs in Nonidentified Models’, Econometric Theory, 14(4), pp 483–509.
Read M (2022a), ‘Algorithms for Inference in SVARs Identified With Sign and Zero Restrictions’, The Econometrics Journal, 25(3), pp 699–718.
Read M (2022b), ‘The Unit-Effect Normalisation in Set-Identified Structural Vector Autoregressions‘, RBA Research Discussion Paper No 2022-04.
Read M and D Zhu (forthcoming), ‘Bayesian Inference in SVARs Using “Soft” Sign Restrictions’, RBA Research Discussion Paper.
Redl C (2020), ‘Uncertainty Matters: Evidence from Close Elections’, Journal of International Economics, 124, Article 103296.
Reichlin L, G Ricco and M Tarbé (2023), ‘Monetary-Fiscal Crosswinds in the European Monetary Union’, European Economic Review, 151, Article 104328.
Romer CD and DH Romer (1989), ‘Does Monetary Policy Matter? A New Test in the Spirit of Friedman and Schwartz’, in OJ Blanchard and S Fischer (eds), NBER Macroeconomics Annual, 4, The MIT Press, Cambridge, pp 121–184.
Rosen AM and T Ura (2020), ‘Finite Sample Inference for the Maximum Score Estimand’, Centre for Microdata Methods and Practice, cemmap Working Paper CWP22/20.
Rothenberg TJ (1971), ‘Identification in Parametric Models’, Econometrica, 39(3), pp 577–591.
Rubio-Ramírez JF, DF Waggoner and T Zha (2010), ‘Structural Vector Autoregressions: Theory of Identification and Algorithms for Inference’, The Review of Economic Studies, 77(2), pp 665–696.
Rüth SK and W Van der Veken (forthcoming), ‘Monetary Policy and Exchange Rate Anomalies in Set-Identified SVARs: Revisited’, Journal of Applied Econometrics.
Sims CA (1980), ‘Macroeconomics and Reality’, Econometrica, 48(1), pp 1–48.
Stock JH and MW Watson (2018), ‘Identification and Estimation of Dynamic Causal Effects in Macroeconomics Using External Instruments’, The Economic Journal, 128(610), pp 917–948.
Uhlig H (2005), ‘What Are the Effects of Monetary Policy on Output? Results From an Agnostic Identification Procedure’, Journal of Monetary Economics, 52(2), pp 381–419.
Uhlig H (2017), ‘Shocks, Sign Restrictions, and Identification’, in B Honoré, A Pakes, M Piazzesi and L Samuelson (eds), Advances in Economics and Econometrics: Eleventh World Congress, Vol 2, Econometric Society Monographs, Cambridge University Press, Cambridge, pp 95–127.
Wolf CK (2020), ‘SVAR (Mis)Identification and the Real Effects of Monetary Policy Shocks’, American Economic Journal: Macroeconomics, 12(4), pp 1–32.
Zhou X (2020), ‘Refining the Workhorse Oil Market Model’, Journal of Applied Econometrics, 35(1), pp 130–140.
Acknowledgements
We thank Isaiah Andrews, Sophocles Mavroeidis, Karel Mertens, José Luis Montiel Olea, Marco Petterson, Mikkel Plagborg-Møller, Franck Portier, Morten Ravn, Christian Wolf and seminar participants at several venues for helpful comments. We gratefully acknowledge financial support from ERC grants (numbers 536284 and 715940) and the ESRC Centre for Microdata Methods and Practice (CeMMAP) (grant number RES-589-28-0001). This is a revised version of a previously circulated working paper, which also formed the basis for Chapter 6 of Matthew Read’s PhD dissertation at University College London. The views expressed in this paper are those of the authors and do not necessarily reflect the views of the Federal Reserve Bank of Chicago, the Federal Reserve System or the Reserve Bank of Australia. Any errors are the sole responsibility of the authors.
Footnotes
CeMMAP and Department of Economics, University College London and Federal Reserve Bank of Chicago [*]
CeMMAP and Department of Economics, Brown University and Department of Economics, University College London [**]
Economic Research Department, Reserve Bank of Australia [***]
Examples of papers imposing NR include Ben Zeev (2018), Altavilla, Darracq Pariès and Nicoletti (2019), Furlanetto and Robstad (2019), Cheng and Yang (2020), Kilian and Zhou (2020, 2022), Laumer (2020), Redl (2020), Zhou (2020), Antolín-Díaz, Petrella and Rubio-Ramírez (2021), Caggiano et al (2021), Larsen (2021), Ludvigson, Ma and Ng (2021), Maffei-Faccioli and Vella (2021), Berger, Richter and Wong (2022), Fanelli and Marsi (2022), Inoue and Kilian (2022), Badinger and Schiman (2023), Berthold (2023), Caggiano and Castelnuovo (2023), Conti, Nobili and Signoretti (2023), Harrison, Liu and Stewart (2023), Herwatz and Wang (2023), Neri (2023), Reichlin, Ricco and Tarbé (2023), Ascari et al (forthcoming), Boer, Pescatori and Stuermer (forthcoming) and Rüth and Van der Veken (forthcoming). [1]
Ludvigson et al (2018, 2021) use a bootstrap to conduct inference, but do not provide evidence about its validity. Existing frequentist approaches to conducting inference in set-identified SVARs include Gafarov, Meier and Montiel Olea (2018) and Granziera, Moon and Schorfheide (2018). [2]
Giacomini, Kitagawa and Read (2022a) explore the performance of the weak-instrument robust frequentist inferential procedures from Montiel Olea, Stock and Watson (2021) when using narrative proxies; these procedures may suffer from size distortions when the sign of the shock is known in a small number of periods. [3]
Giacomini, Kitagawa and Read (2022b) extend this approach to SVARs where the parameters of interest are set identified using external instruments, or ‘proxy SVARs’. See Giacomini, Kitagawa and Read (2021) for a survey of the literature on robust Bayesian methods, including a discussion of different approaches to conducting robust Bayesian inference in set-identified SVARs. [4]
The data-generating process assumes vec(A0) = (1,0.2,0.5,1.2)′, which implies that and with Q equal to the rotation matrix. We assume the time series is of length T = 3 and draw sequences of structural shocks such that T is a small number to control Monte Carlo sampling error. The analysis with set to its true value replicates the situation with a large sample, where the likelihood for concentrates at the truth. It also facilitates visualising the likelihood, which otherwise is a function of four parameters. [5]
See, for example, Uhlig (2005), Rubio-Ramírez, Waggoner and Zha (2010) and Arias, Rubio-Ramírez and Waggoner (2018). [6]
The VAR(p) is invertible into a VMA process when the eigenvalues of the companion matrix lie inside the unit circle. See Hamilton (1994) or Kilian and Lütkepohl (2017). [7]
Ch can be defined recursively by for with C0 = In. In practice Ch can be computed using the companion form of the VAR. [8]
Ben Zeev (2018) imposes a restriction on the timing of the maximum three-year average of a particular shock, as well as restrictions on the sign and relative magnitudes of this three-year average in specific periods. Restrictions on averages of shocks can also be implemented in this framework. An earlier version of our paper considered the restriction that the shock in a particular period was the largest (absolute) realisation of the shock in the sample period; see also Read (2022a). [9]
GK21 explicitly allow for zero restrictions in their robust Bayesian analysis of set-identified SVARs. Giacomini et al (2022b) extend this to proxy SVARs. Read (2022b) imposes sign, narrative and zero restrictions within our robust Bayesian framework. [10]
See Plagborg-Møller (2019) for a discussion of this point in the context of structural VMA models. [11]
is observationally equivalent to if holds for all yT and . [12]
Under the restriction on the historical decomposition, a notable difference between the conditional and unconditional likelihood cases is the slope of the squared Hellinger distance around the minimum. The squared Hellinger distance of the unconditional likelihood has a steeper slope than the conditional likelihood. This indicates the loss of information for in the conditional likelihood due to conditioning on a non-ancillary event. [13]
See also Komarova (2013) for the construction of identified sets for maximum score coefficients with discrete regressors. [14]
Based on the results in Arias et al (2018), AR18 argue that their algorithm draws from a normal-generalised-normal posterior for the SVAR's structural parameters (A0,A+) induced by a conjugate normal-generalised-normal prior, conditional on the restrictions. [15]
is defined as a shortest interval among the connected intervals satisfying See Proposition 1 in GK21 for a procedure to compute the volume-minimising credible region. [16]
The results are not directly comparable to those in Figure 6 of AR18. First, we present responses to a standard deviation shock, whereas AR18 normalise the median impact response of the federal funds rate to 25 basis points. Second, our prior for Q is conditionally uniform, whereas the prior in AR18 is unconditionally uniform. They also use the conditional likelihood to construct the posterior. [17]
This is the algorithm used by Rubio-Ramírez et al (2010) to draw from the uniform distribution over , except that we do not normalise the diagonal elements of R to be positive. This is because we impose a sign normalisation based on the diagonal elements of in Step 2.2. [18]
Read and Zhu (forthcoming) develop more computationally efficient algorithms for obtaining draws of Q from a uniform distribution over the (conditional) identified set given a broad class of identifying restrictions, including NR. [19]
Giacomini and Kitagawa (2021b) present similar conditions for SVARs identified using traditional signs and/or zero restrictions. It would be straightforward to extend the conditions here to additionally allow for sign and zero restrictions on the first column of Q. [20]
For a vector means that for all i = 1,...,m. [21]