RDP 2022-04: The Unit-effect Normalisation in Set-identified Structural Vector Autoregressions 3. The Unit-effect Normalisation in a Bivariate SVAR
October 2022
- Download the Paper 2,225KB
This section uses a stylised model to explain how identified sets for unit impulse responses can be unbounded, and to draw out some implications for conducting inference. The model is a bivariate SVAR with no dynamics, which is identified using sign restrictions on impulse responses. This simple setting allows me to analytically derive identified sets for the impulse responses. The features of this example extend straightforwardly to more general settings. See Appendix A for derivations of the results in this section.
Baumeister and Hamilton (2015) use the same bivariate model to show that the standard uniform prior over Q is informative about impulse responses (in the sense that the implied conditional prior over the impulse responses is generally non-uniform). In particular, the implicit conditional prior (and posterior) for the unit impulse response is a Cauchy distribution that is truncated by the sign restrictions, where the points of truncation depend on the reduced-form parameters. As part of this exercise, they show that the identified set for the unit impulse response is unbounded.[9]
3.1 Identified sets for impulse responses to unit shocks
The model is where and The orthogonal reduced form of this model is where is the lower-triangular Cholesky factor of and Q is a 2×2 orthonormal matrix. The space of 2×2 orthonormal matrices can be represented as
where the first set is the set of ‘rotation’ matrices and the second is the set of ‘reflection’ matrices. Henceforth, I leave it implicit that
In the absence of any identifying restrictions, the identified set for (the matrix of impact impulse responses) is
and the identified set for A0 (the matrix of structural coefficients) is
Throughout, I impose the ‘sign normalisation’ which is a normalisation on the signs of the structural shocks (e.g. a positive value of corresponds to an increase in y1t holding y2t fixed).
Consider the case where the impact response of the first variable to the first shock is restricted to be non-negative and the impact response of the second variable to the first shock is restricted to be non-positive The identifying restrictions generate an identified set for , which can in turn be used to obtain an identified set for
The identified set for excludes zero when but it includes zero when The sign restrictions therefore do not rule out the possibility that the first variable does not respond to the first structural shock.
The impulse response of the second variable to a unit shock in the first variable is
The identified set for this impulse response is
When , the lower bound of this identified set is negative and finite, while the upper bound is zero. In contrast, when , the identified set for is unbounded below; diverges to approaches (the lower bound of the identified set for ) from above, which is equivalent to approaching zero from above. The upper bound of the identified set for this impulse response is equal to zero, so the sign restrictions are completely uninformative about outside of its sign (which is imposed).
Figure 1 provides some geometric intuition behind this result. Since the identifying restrictions constrain q1 only, they can be represented as three half-spaces (corresponding to the sign normalisation plus the two sign restrictions on impulse responses) in two-dimensional space. Since q1 has unit length, the identified set for q1 is given by the intersection of these half-spaces with the unit circle. When the identified set includes the boundary of the half-space corresponding to the sign restriction can be made arbitrarily large by considering a sequence for q1 converging to the point of singularity, Whether it is possible to do this depends on the sign of When the intersection of the half-spaces always excludes the point of singularity (Panel A). In contrast, the point of singularity is included within the identified set when (Panel B).[10]
For alternative economic intuition, consider interpreting the bivariate model as a model of supply and demand, with y1t log price and y2t log quantity. The sign restrictions require price and quantity to move in opposite directions in response to a shock in the first equation of the model, which implies that this equation can be interpreted as a supply curve and as a supply shock. is then the response of quantity to a supply shock that raises price by 1 per cent (i.e. the price elasticity of demand). When the identifying restrictions do not rule out the possibility that the demand curve is horizontal (which occurs when ). In the limit as the demand curve approaches being horizontal, it takes a larger shift in the supply curve and a larger fall in quantity for price to rise by 1 per cent (Figure 2). The fall in quantity required for price to fall by 1 per cent can be made arbitrarily large by making the demand curve arbitrarily flat.
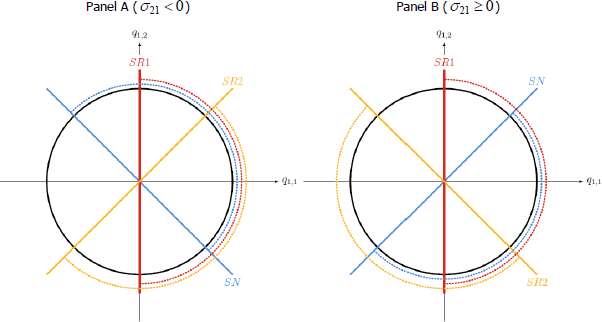
Notes: This figure depicts the identified set for q1 = (q1,1, q1,2) under the identifying restrictions described in the text and assuming that and (Panel A) or 0.5 (Panel B). The black circle is the unit circle. The coloured lines represent the boundaries of the half-spaces generated by the identifying restrictions: ‘SN’ corresponds to the sign normalisation ‘SR1’ corresponds to the sign restriction ‘SR2’ corresponds to the sign restriction The dashed arcs represent the sets of values of q1 satisfying each individual restriction; the arc of the unit circle where the three dashed arcs overlap is the identified set for q1.
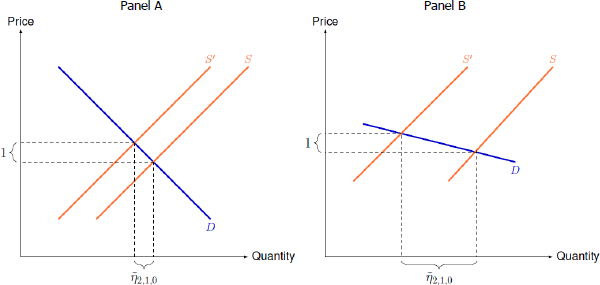
Notes: This figure depicts the shift in the supply curve (from S to S') required to induce a 1 per cent increase in price under differently sloped demand curves (D). The corresponding decrease in quantity is the impulse response to a unit supply shock. This becomes arbitrarily large as the demand curve approaches the horizontal.
Note that unboundedness of the identified set also arises when imposing sign restrictions on multiple columns of Q (i.e. on impulse responses to multiple shocks). When additionally imposing that the impulse responses of both variables to the second shock are positive, the identified set for continues to include zero when and the identified set for is unbounded (see Appendix A.2 for details). Unboundedness of the identified set also occurs when imposing sign restrictions with strict, rather than weak, inequality. Strict inequality restrictions yield identified sets that are open, rather than closed, intervals, but the identified set for remains unbounded when Finally, unboundedness of the identified set does not arise purely due to working in the orthogonal reduced-form parameterisation and defining the unit impulse response as the ratio of impulse responses to standard deviation shocks; that is, it also arises when using a parameterisation that imposes the unit-effect normalisation directly (see Appendix A.3).
This stylised example highlights that the identified set for unit impulse responses may be unbounded if the identified set for the impact response of the normalising variable to a standard deviation shock includes zero. Whether this is the case depends on the values of the reduced-form parameters. The following sections discuss some implications of unboundedness for conducting inference about unit impulse responses.[11]
3.2 Robust Bayesian inference under unboundedness
This section discusses how unboundedness of the identified set affects different inferential outputs (e.g. sets of posterior means or quantiles) under the robust Bayesian approach to inference. To aid explanation, I continue to frame the discussion through the lens of the bivariate model. I also make the simplifying assumption that is supported only on two values of the reduced-form parameters: and where However, the results extend straightforwardly to more general settings. I denote the lower bound of the identified set for when and the posterior probability that The identified set for with posterior probability and it is with posterior probability
Set of posterior means. The set of posterior means, which has bounds equal to the posterior means of the bounds of the identified set, will be unless Consequently, if places positive posterior probability on the event the set of posterior means is completely uninformative about (other than its sign, which is imposed by the sign restrictions).
Sets of posterior quantiles. The set of posterior medians is an interval with lower (upper) bound equal to the posterior median of the lower (upper) bound of the identified set. The median of the upper bound of the identified set is zero regardless of the value of . When the posterior median of the lower bound of the identified set is The set of posterior medians will therefore be bounded. In contrast, when the posterior median of the lower bound of the identified set is so the set of posterior medians is unbounded. By similar logic, the set of posterior -quantiles will be bounded so long as The class of posteriors may therefore still contain useful information about particular posterior quantiles even when the identified set is unbounded with positive posterior probability.
Robust credible intervals. A robust credible interval with credibility can be constructed by taking the quantile of and the quantile of . Whether the robust credible interval is bounded will therefore depend on the credibility level and In particular, boundedness of the robust credible interval requires that the sets of and quantiles are both bounded, which will be the case in the current example if
Posterior lower and upper probabilities. Consider the hypothesis that for some . The posterior lower probability of this hypothesis is equal to the posterior probability that the identified set is contained within the interval . This probability is zero for all x < 0. The posterior upper probability of the hypothesis is equal to the posterior probability that the identified set intersects the interval . The posterior upper probability is one for and is for The set of posterior probabilities for the hypothesis is therefore [0,1] for and is for As approaches zero, so that the identified set is almost always unbounded, the set of posterior probabilities converges to the unit interval for all values of x. In this case, the sign restrictions are not informative about the hypothesis regardless of the value of x. In contrast, as approaches one, the set of posterior probabilities converges to zero for sufficiently negative values of x (i.e. for ). In this case, ‘large’ responses are assigned low posterior probability regardless of the choice of conditional prior.
Summary. This discussion illustrates that it is possible to extract useful information about the impulse responses to a unit shock using the robust Bayesian approach to inference when the identified set is unbounded with positive posterior probability. Moreover, understanding how often the identified set is unbounded (in terms of posterior probability) is valuable for understanding which inferential outputs themselves will be unbounded, and thus for gauging the informativeness of the identifying restrictions.
3.2.1 Frequentist validity
For general set-identified models, Giacomini and Kitagawa (2021) provide high-level conditions under which their robust Bayesian approach to inference has a valid frequentist interpretation, in the sense that the set of posterior means is consistent for the true identified set (i.e. the identified set when is equal to its true value, ) and the robust credible interval has correct frequentist coverage for the true identified set. In the context of SVARs and when the parameter of interest is an impulse response to a standard deviation shock, Giacomini and Kitagawa provide sufficient conditions under which these high-level conditions will hold. In particular, the set of posterior means can be interpreted as a consistent estimator of the true identified set if the identified set is convex and continuous at Additionally, if the end points of the identified set are differentiable in at and have non-zero derivatives, the robust credible interval has valid frequentist coverage of the true identified set.
When the parameter of interest is a unit impulse response, the high-level conditions for frequentist validity of the robust Bayesian approach are not necessarily satisfied. For example, these conditions include the assumption that the true identified set is bounded. Consequently, the robust Bayesian approach to inference is not guaranteed to have an asymptotically valid frequentist interpretation when the parameter of interest is a unit impulse response.
To illustrate, consider the bivariate model and assume that is such that so the true identified set is unbounded. For values of in a small neighbourhood of and so naively applying the robust Bayesian approach in this case will almost surely yield a robust credible interval of asymptotically. Clearly, this interval always (weakly) includes the true identified set, so the asymptotic frequentist coverage probability will be trivially equal to one (i.e. the robust credible interval is conservative).[12]
3.3 Frequentist estimation under unboundedness
Unboundedness may also arise when estimating or conducting inference about unit impulse responses in a frequentist framework. Let be the MLE of If is such that a frequentist estimate of the identified set for – which simply plugs the MLE of into the expression for the identified set given in Section 3.1 – will be bounded. In contrast, if is such that a frequentist estimate of the identified set for will be unbounded.
Footnotes
Baumeister and Hamilton (2018) also note that the identified set may be unbounded (see their Footnote 4, p 50). [9]
When imposing only the sign normalisation, the identified set for is always in this case, it is possible to approach the point of singularity from the positive or negative direction regardless of the value of When imposing the sign normalisation and the sign restriction the identified set for is always in this case, the point of singularity can be approached from the positive direction only. [10]
Identified sets can also be unbounded when the parameter of interest is the structural coefficient on a particular variable after normalising the coefficient on another variable to equal unity (i.e. the ratio of elements of A0), which may be interpretable as a structural elasticity (e.g. Baumeister and Hamilton 2022). If the identified set for the normalising coefficient includes zero, the identified set for the ratio of coefficients may be unbounded. [11]
In the current bivariate example and when is such that the true identified set is bounded, but the robust credible interval has an asymptotic frequentist coverage probability equal to (i.e. the robust credible interval is conservative). This arises because the upper bound of the identified set is degenerate and is therefore not differentiable in with non-zero derivative. When there are additional sign restrictions on the impulse responses to the second shock, both the lower and upper bound are differentiable in (see Appendix A.2), and the robust credible interval has correct coverage asymptotically. [12]