RDP 2021-03: Financial Conditions and Downside Risk to Economic Activity in Australia 2. Modelling Risks to Economic Activity from Changing Financial Conditions
March 2021
- Download the Paper 1,967KB
We follow a four-step process to model the risks posed to economic activity from financial conditions:
- We develop a summary indicator to represent ‘financial conditions’ (the FCI), which will be an explanatory variable in subsequent regressions.
- We estimate the conditional distribution of future economic activity given current economic activity and the FCI using a novel quantile regression approach known as ‘quantile spacings’. This yields a series of fitted regressions for discrete quantiles of the distribution over time – for example, one equation for the 0.05 quantile (5th percentile) of the distribution of future economic activity, one equation for the 0.25 quantile, and so on.
- We compute a sequence of probability density functions (PDFs) by mapping the estimated discrete quantiles at each point in time to a (continuous) skewed t distribution.[2]
- We use these smoothed PDFs to quantify downside risk to future economic activity by measuring the area in the left tail of the distributions. This measure of risk is known as ‘expected shortfall’. It measures the average severity of extreme tail events given that a loss has occurred (that is, it abstracts from the probability of a loss occurring in the first place). In contrast, the more well-known VaR measure conflates the magnitude of the potential loss with the probability of it occurring.[3]
2.2 A summary indicator of financial conditions in Australia
To implement the GaR framework for Australia we require a summary indicator of financial conditions that are not otherwise directly observable. Since there is currently no existing indicator available for Australia, our first task is to develop an FCI. We follow previous work by other central banks (e.g. Brave and Butters 2010) and construct our FCI using a dynamic factor model (DFM). The model incorporates 75 individual data series covering various aspects of the financial system, including measures of: asset prices; interest rates and spreads; credit and money; debt securities outstanding; leverage; banking sector risk; financial system complexity; financial market risk; and survey measures of businesses' and consumers' views on financial conditions. Within these categories, we include a mix of Australian and US variables, with the US data included to capture spillover effects from US financial variables to other markets (Zdzienicka et al 2015). The FCI is constructed at a quarterly frequency, to match both the lowest frequency of its individual component series and the lowest frequency of the economic variables we are trying to predict.[4],[5] Appendix A.1 describes the dataset in more detail, while Appendix A.2 describes the methodology used to construct the index and Appendix A.3 sets out which components have had the most influence on the overall measure. The appropriateness of the estimation method used for the FCI is examined in Appendix A.4 and Appendix A.5 focuses on assessing the correlations between the FCI and 5 measures of economic activity, including through Granger causality tests.
Figure 1 illustrates our estimated FCI for the time period 1976:Q4 to 2020:Q3.[6] The FCI can be interpreted as indicating that financial conditions are generally ‘restrictive’ when it takes on values greater than zero, and generally ‘expansionary’ when it takes on values less than zero.[7] The shaded region in the figure is the 95 per cent confidence interval for the FCI and its narrowness indicates that our estimate is relatively precise.[8] This high degree of precision is important as it reduces – though does not eliminate – concerns about estimation uncertainty from the use of the FCI as a ‘generated regressor’ in our subsequent quantile regressions (Bai and Ng 2006).
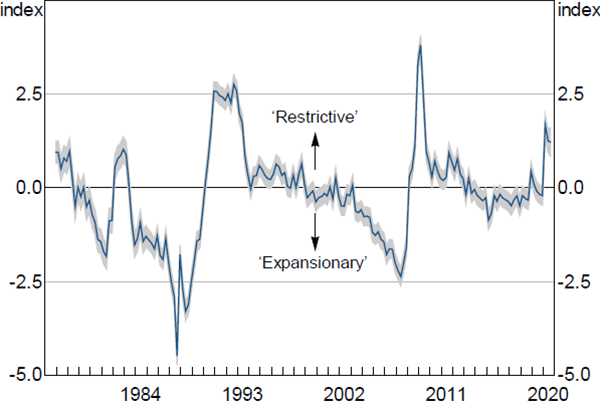
Note: Shaded region represents 95 per cent confidence interval
Movements in the FCI correspond to known historical events. For example, the FCI suggests financial conditions were more expansionary in the late 1980s, consistent with the rapid growth in credit and asset prices (particularly residential and commercial property prices) over that period. However, financial conditions became very restrictive around the time of the early 1990s recession as credit supply contracted sharply and commercial property prices fell from very high levels. From the mid 1990s to the early 2000s the FCI remained around zero, corresponding with the start in Australia of the period now referred to as the ‘Great Moderation’ (Simon 2001). The FCI indicates financial conditions became more expansionary from around 2006–07 before tightening significantly during the GFC (i.e. 2008–09).
More recently, financial conditions deteriorated sharply with the onset of the COVID-19 pandemic, driven in particular by declines in asset prices, weaker growth in measures of credit and money and heightened measures of financial market risk. Notably, however, our estimates suggest that financial conditions since March 2020 have not been as restrictive as they were during the GFC, similar to the results of Groen, Nattinger and Noble (2020). While this is likely due in part to the significant policy responses by central banks, fiscal authorities and financial system supervisors, it also reflects the improved resilience of the financial system since the GFC (Kearns 2020).
In addition to having a reasonably close correlation with major historical events, Granger causality tests confirm that the FCI contains predictive information about each of the 5 measures of economic activity considered in this paper (GDP, household consumption, business investment, employment and the unemployment rate). This suggests that the FCI is not simply capturing information that is already directly available from the economic variables themselves.
Having constructed an FCI with a number of appealing properties, the next step is to incorporate it into our GaR framework using the three-stage approach described below.
2.3 Stage 1: modelling the distribution of economic activity for discrete quantiles
In the first stage, we employ a variant of quantile regression (QR) to model the conditional relationship between future economic activity (the dependent variable, denoted as yt+h where h is the forecast step length) and current economic activity, current financial conditions and a constant (the explanatory variables, collectively denoted as xt). Current financial conditions are measured by the FCI.
In contrast to ordinary least squares (OLS) regressions, which estimate the conditional mean of the dependent variable, quantile regressions estimate the entire conditional distribution of the dependent variable. That is, the location, scale and shape of the distribution of the dependent variable is determined by the explanatory variables and the explanatory variables are able to have different effects on different parts of the distribution. However, one problem with using a standard QR approach when implementing the GaR framework is that it can generate quantile estimates that cross (Carriero, Clack and Marcellino 2020). This is problematic because a quantile function is, by definition, monotonic (e.g. the 0.05 quantile always lies below the 0.1 quantile), but this important property is violated if quantiles cross (e.g. the model predicted value for the 0.05 quantile lies above the prediction for the 0.1 quantile).
The crossing problem is more likely to be an issue with models that include lags of the dependent variable. This is because the set of explanatory variables that are used in estimation is determined within the model (Koenker 2005). Additionally, when crossing does occur, it is generally confined to the outlying regions of the sample space, which could affect our ability to estimate downside risk.
To avoid this potential issue, we use the ‘quantile spacing’ method proposed by Schmidt and Zhu (2016) for estimating multiple conditional quantiles. In addition to enforcing the monotonicity of the estimated quantiles, the authors show that their model can potentially better capture nonlinearities in data as well.[9] This makes the quantile spacing technique ideal for modelling GaR. It works by first modelling the level of a central quantile and then adding/subtracting a series of ‘spacing functions’ to produce the other, non-crossing, quantiles.
More formally, the quantile spacing method can be described as follows. Let be the conditional quantile function of yt+h for each quantile (0,1) such that:
Our goal is to estimate a model for p conditional quantiles associated with the quantiles and we label the jth conditional quantile of interest by Specifically, we parameterise the individual conditional quantiles as:
The process starts by modelling the level of a central quantile, which we set to be the conditional median. That is, = 0.5 for {1,...,p}. Then all other quantiles of interest are defined by adding/subtracting a series of non-negative spacing functions to this central quantile. This ensures that all quantiles will be monotonic by construction.[10]
The method we use for estimating the various coefficients follows the iterative process outlined in Schmidt and Zhu (2016). Note the interpretation of an individual coefficient within each of the spacing functions differs from a standard QR model. In this framework they represent a semi-elasticity. That is, for any , we have that:
which is the percentage change in the distance between two quantiles caused by a marginal change in xt. A positive value in a spacing below (above) the central quantile indicates that increasing xt increases downside (upside) risk by flattening the left (right) tail, all else equal.
We fit the model using quantiles = {0.05, 0.25, 0.50, 0.75, 0.95} and estimate the distribution of economic activity one quarter ahead (i.e. h = 1) for quarterly growth and 4 quarters ahead (i.e. h = 4) for year-ended growth. Besides the inclusion of the median, these are the same values originally specified by Adrian et al (2019).[11] The estimation period is 1976:Q4 to 2020:Q2, which is the minimum available sample period for our national account measures of economic activity. The main output of this process is a set of predicted values for each quantile of the distribution of economic activity over time denoted as
2.4 Stage 2: constructing a sequence of PDFs of economic activity
After fitting the quantile regression using the quantiles specified by , the next stage is to construct a sequence of continuous PDFs. We do this by mapping the fitted values from the quantile regressions onto a parametric distribution. This serves to smooth the fitted quantile regression values and provides a complete PDF. This, in turn, allows us to quantify GaR as the area in the tails of the distribution using integration. We follow Adrian et al (2019) and choose the skewed t distribution (ST).[12] The version of the ST distribution we use is the one proposed by Hansen (1994).[13] It is defined by the PDF:
where is the Gamma function, is the location of x and is the scale term. The parameter controls the skewness while q is the degrees of freedom term which controls the ‘heaviness’ of the tails (and the probability of outliers). The distribution is symmetric for = 0 and positively skewed for positive values of and vice versa.[14]
We estimate the four parameters which characterise the ST distribution for each time period in the sample. We do this by minimising the sum of squared errors between the set of fitted quantile functions and the theoretical ST distribution quantile function based on the 0.05, 0.25, 0.50, 0.75 and 0.95 quantiles as follows:
This can be viewed as an over-identified nonlinear cross-sectional regression of the predicted quantiles on the theoretical quantiles of the ST distribution.[15] With these 4 sequences of estimated parameter values we can construct a sequence of skewed t PDFs for each time period by plugging the values obtained for the 4 parameters at each time period into Equation (4).
2.5 Stage 3: quantifying tail risks to economic activity
Once we have our estimated sequences of predicted PDFs we can quantify downside and upside risks to future economic activity using expected shortfall and its counterpart, expected ‘long rise’. These two measures of risk are preferable to VaR since they summarise the tail behaviour of the estimated distribution of economic activity in absolute terms. Both measures are calculated for a given threshold quantile and are defined to be the average loss (gain) in economic activity given that a loss (gain) has occurred at or below (above) that quantile (i.e. the VaR threshold). That is, they provide a numerical answer to the question: if economic activity exceeds the quantile threshold, how bad (good) could economic outcomes be on average? In practice, this is achieved by measuring the area under the predicted PDF below (above) the relevant quantile. We can define these measures of tail risk more formally as:
Our focus will be on downside risk as measured by expected shortfall (SFt+h), but we will also highlight upside risk using expected long rise (LRt+h) to show that economic activity can respond asymmetrically to tighter and looser financial conditions.
Footnotes
We use a continuous distribution because computing the area in the tails requires us to use (numerical) integration. [2]
An additional technical reason for preferring expected shortfall over VaR is that it is a ‘coherent’ measure of risk while VaR is not. This is because VaR violates the sub-additivity property. [3]
We convert any series available at higher frequencies to a quarterly frequency by computing the quarter average for ‘flow’ variables or using the quarter-ended value for ‘stock’ variables. [4]
The FCI developed by Hatzius et al (2010) for the United States is also quarterly. [5]
The estimated FCI for September quarter 2020 includes only 42 of the 75 variables owing to data availability at the time of estimation. [6]
There is no clear convention regarding the sign of the FCI, but we follow the Federal Reserve Bank of Chicago in defining more restrictive conditions with positive values and expansionary conditions with negative values. Appendix A.2 describes how we implement this specific sign convention when estimating the FCI. [7]
The narrowness of the estimated confidence interval is related to the number of variables in our dataset ( N ), which is large relative to the number of observations for each variable ( T ). [8]
In an empirical application related to forecasting the distribution of stock returns, Schmidt and Zhu (2016) show that their method outperforms the standard QR method for most quantiles, especially on the lower tail of the distribution. They suggest this could translate into a better estimate for tail measures such as VaR. [9]
A second issue with standard QR discussed in Carriero et al (2020) concerns estimating tail quantiles with small sample sizes. The problem relates to quantile estimates that can be seen as unrealistically extreme. The quantile spacing method is also susceptible to this issue given the use of the exponential function in Equation (2). To mitigate this problem we use a form of winsoring when constructing the quantile estimates. [10]
In the quantile spacing setting, Schmidt and Zhu (2016) suggest these particular values will also characterise the effect of a one unit change in our explanatory variables on the width of the left tail, left shoulder (i.e. the area between the peak of the distribution and the tail), right shoulder and right tail of the distribution. [11]
This distribution is very flexible and nests other well-known distributions, including the Gaussian, Laplace, Student's t or Cauchy. [12]
This ST specification differs to Adrian et al (2019) who use the ST distribution developed by Azzalini and Capitanio (2003). We chose the version proposed by Hansen (1994) for computational reasons. [13]
The parameters of the ST distribution have the following restrictions: and q > 0. If the ST becomes the Student's t distribution. If the ST becomes a skewed Gaussian distribution. If and the ST becomes the Gaussian distribution. [14]
We employ parameter transformations on and when solving the minimisation problem to the ensure the ST parameter restrictions are enforced. [15]