RDP 2020-02: The Distributional Effects of Monetary Policy: Evidence from Local Housing Markets 6. Robustness Tests
February 2020
- Download the Paper 1,879KB
6.1 Alternative Measures of Monetary Policy
We re-estimate the unrestricted model but replace the cash rate with a plausibly exogenous measure of monetary policy. Following Romer and Romer (2004), we estimate a series of monetary policy ‘shocks’. Unlike our baseline models, these shocks attempt to isolate the unexpected component of monetary policy changes.
This monetary policy shock series is constructed by purging changes in the cash rate of information in the Reserve Bank's forecasts of unemployment, real GDP and inflation (Bishop and Tulip 2017). Following Beckers (2020), this shock measure is extended to also account for credit spreads and we also include an autoregressive (AR(1)) forecast of housing prices. We include credit spreads as they appear to have predictive power over and above the Reserve Bank's forecasts in forecasting cash rate changes. Moreover, accounting for an AR(1) forecast of housing prices explicitly models any response in the cash rate to housing price information.[26]
Where:
- is the quarterly change in the cash rate;
- is the quarterly lag of the cash rate level;
- represents the Reserve Bank's forecasts and forecast revisions of real GDP, inflation and unemployment (two-quarters-ahead);
- CSt is a measure of credit spreads used in Beckers (2020), including: the spread between the 3-month bank-accepted bill (BAB) rate and the 3-month Australian dollar overnight indexed swap (OIS), the spread between the average large business variable lending rate and the 3-month BAB rate, and the US BAA 10-year spread;
- is an AR(1) forecast and forecast revisions of real housing prices (two-quarters-ahead).
The estimated residuals represent monetary policy shocks (or deviations from a forward-looking monetary policy rule). Substituting the monetary policy shocks in place for cash rate changes gives us the following equation:
where is the estimated effect of monetary policy on housing prices for region i.
Using this alternate measure of monetary policy in the unrestricted model produces quite a different distribution of housing price responses. Figure 7 compares the distribution of responses using the Romer and Romer-style shocks against the cash rate changes. The results suggest that two years after a 100 basis point increase in monetary policy the median area experiences a 9 percentage point decline in housing prices, while the 25th and 75th percentiles experience declines of 4 per cent and 14 per cent, respectively. The centre of the distribution differs, and the variance of the distribution is clearly larger. This provides further evidence that monetary policy has strong distributional effects across local housing markets. And it may suggest that there are other unobserved factors that drive both changes in monetary policy and heterogeneous effects across local housing markets that are not well captured by the controls for macroeconomic conditions. However, we believe that mismeasurement is also an issue with these shocks as demonstrated by the greater uncertainty around the estimates.
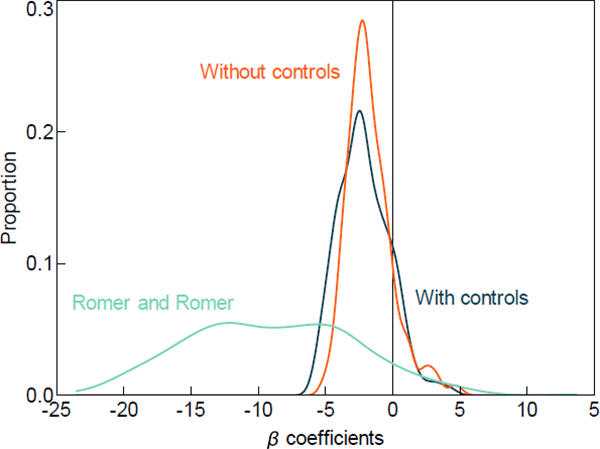
Sources: ABS; Authors' calculations; CoreLogic data; RBA
6.2 Alternative Measures of Local Housing Markets
It may be the case that the results from the restricted model are affected by the differences between metropolitan and regional local housing markets. To explore whether metropolitan and regional areas display different levels of heterogeneity, we re-estimate the restricted model using only the sample of metro areas. By removing areas outside of the greater capital cities, the sample of local housing markets is reduced to 156. We divide these metro areas into price quintiles to account for the smaller number of areas.
The results suggest that the variation in housing price responses across local housing markets is only partially explained by differences between regional and metro areas (Figure 8). Even within metro areas, in response to an increase in the cash rate more expensive markets experience larger falls in housing prices relative to the median. This is consistent with the earlier observation that, even within states, housing price growth can vary substantially.
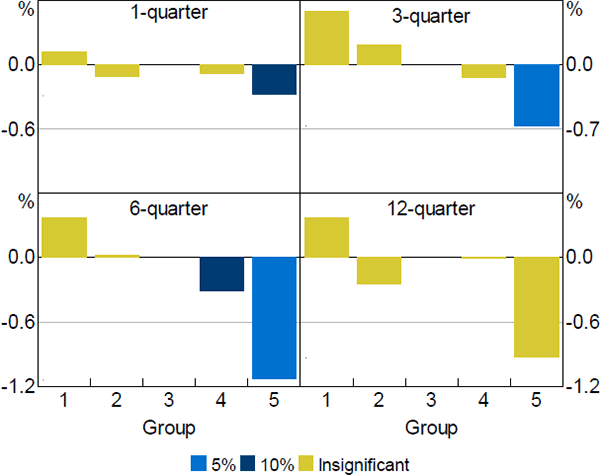
Notes: Colours represent level of significance of estimated coefficients using standard errors clustered across time and state (or territory); price quintiles are calculated using only metropolitan areas
Sources: ABS; Authors' calculations; CoreLogic data; RBA
Footnote
It is possible to calculate the absolute effects of monetary policy on housing prices across regions using these shocks. However, an ideal measure of monetary policy shocks would purge changes in the cash rate only from anticipated changes in housing prices. This measure purges more than just the anticipated changes. [26]