Research Discussion Paper – RDP 2020-02 The Distributional Effects of Monetary Policy: Evidence from Local Housing Markets
1. Introduction
‘… it is pretty clear that there is no such thing as the Australian housing market. What we have is a series of separate, but interconnected, markets.’ (Lowe 2019)
It is well known that the price of housing is sensitive to changes in interest rates (e.g. Himmelberg, Mayer and Sinai 2005; Jorda, Schularick and Taylor 2015; Williams 2016; Gibbs, Hambur and Nodari 2018; Saunders and Tulip 2019). It is also well known that the price of housing varies by location (e.g. Glaeser, Gyourko and Saks 2006; Saiz 2010). And yet we know little about how these findings fit together. Do interest rates contribute to housing price variation across regions? Are housing prices in more expensive areas more sensitive to interest rates than in cheaper areas? If so, by how much? And what does this tell us about the transmission of monetary policy?
The variation in housing price cycles is clear in Australia, both between and within states (Figure 1). For example, the two most populous states of New South Wales and Victoria experienced strong run-ups in housing prices between 2013 and 2017, followed by relatively steep falls. In comparison, the Northern Territory experienced a steep decline in housing prices over the same period. Looking within states, the more expensive areas of New South Wales and Victoria saw much larger increases in housing prices than cheaper areas during the recent upswing.
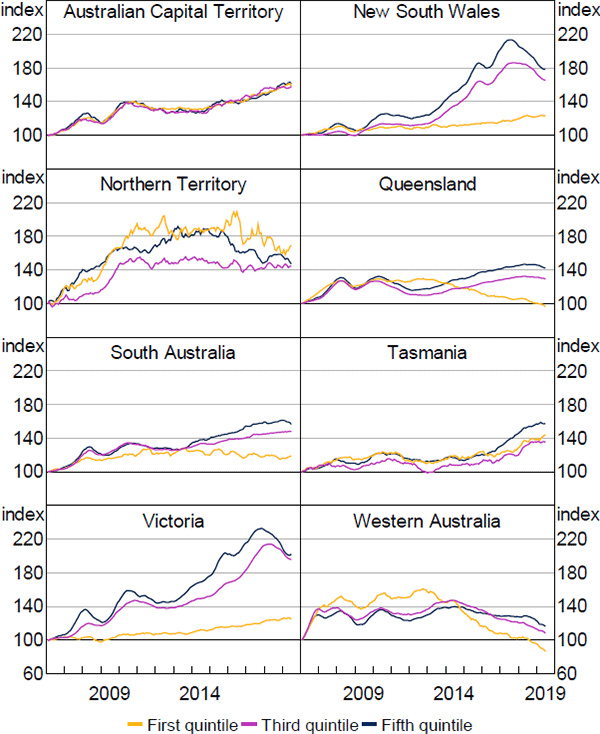
Note: Price quintiles are calculated within state or territory
Sources: Authors' calculations; CoreLogic data
In this paper we explore the distributional effects of monetary policy on housing prices across local housing markets in Australia. In studying the effects of monetary policy, the varying housing market experiences both between and within states and territories is important for a couple of reasons.
First, the distribution of housing prices helps to identify the causal effects of monetary policy. The relationship between housing prices and monetary policy is typically identified using time series models that are subject to endogeneity problems. For instance, the central bank may raise interest rates if it expects the economy to be stronger in the future. At the same time, asset prices, including housing prices, may rise if households also expect higher future economic growth. This will confound any results and likely attenuate estimates; clouding the true effect of monetary policy on the housing market. In this example, it may appear that increases in monetary policy lead to increases in housing prices, when in reality it is stronger expected economic growth that drives both. By exploiting the fact that the central bank is unlikely to systematically respond to conditions in any specific local housing market we can better identify the effects of monetary policy.
Second, the distribution can tell us why monetary policy works. Any regional variation in the sensitivity to monetary policy may tell us why monetary policy matters to the housing market. For example, expensive areas may be more supply constrained than cheaper areas given they are more likely to be in coastal areas. If a demand shock due to a change in interest rates has a greater effect on housing prices in these areas, then this may tell us that supply constraints are binding and important to the transmission of monetary policy to housing markets. In other words, the economy may be more sensitive to monetary policy if more areas are supply constrained (holding all else constant). This information could be important to take into account when setting monetary policy.
To study the distributional effects of monetary policy, we estimate a model in which each local housing market is allowed to respond differently to monetary policy. The resulting distribution of price sensitivities across local markets provides information about the factors that link monetary policy and the housing market. When interest rates fall, areas with less elastic housing supply should experience larger increases in housing prices than areas with more elastic supply (Aastveit and Anundsen 2016). Consistent with this, we find that supply-related factors, such as land availability, explain some of the cross-sectional variation in local housing price sensitivities. But other factors are relevant too. For example, housing prices are more sensitive to monetary policy in regions with higher shares of housing investors and higher levels of income, on average. These findings are consistent with research that emphasise the role of expectations in driving housing price dynamics (e.g. Kaplan, Mitman and Violante 2019).
We also find that the local housing markets with relatively high levels of mortgage debt are those in which local housing prices are more sensitive to changes in monetary policy. This result is consistent with research that suggests that monetary policy has state-dependent effects, wherein the state of the mortgage market affects the potency of monetary policy (Beraja et al 2019).
We then directly study the effects of monetary policy on housing wealth inequality. For this, a specific version of the model is estimated in which local housing markets are sorted by how expensive they are.[1] We find that more expensive regions are more sensitive to changes in monetary policy. The variation in price responses across regions also suggests that reductions in the cash rate increase housing wealth inequality. However, this effect appears temporary with the price differences between regions disappearing about two years after the interest rate change. We investigate if this differential is linked to land availability and supply constraints, and find some evidence to support this with the effect being more concentrated in areas that have higher land availability constraints. However, we are not able to rule out other channels by which monetary policy could generate changes in the housing wealth distribution.
This paper is closely related to several papers that study the effect of monetary policy on regional housing markets. Most of this research focuses on the United States.[2] Consistent with our findings for Australia, there is substantial variation across US local housing markets in the sensitivity of housing prices to monetary policy (Cooper, Luengo-Prado and Olivei 2016; Fischer et al 2018).[3] This heterogeneity is typically linked to variation in housing supply elasticities (Aastveit and Anundsen 2016) and, more specifically, to variation in local government regulations (Fischer et al 2018). There is also some evidence of asymmetric effects of monetary policy across US local housing markets (Aastveit and Anundsen 2016). However, some studies suggest that monetary policy has a limited role to play in explaining the variation across local housing markets (Del Negro and Otrok 2007).[4] Moreover, while many studies suggest that regional heterogeneity is due to supply-side factors, other potential explanations could be important too (e.g. Fischer et al 2018; Beraja et al 2019).[5]
This paper is also related to a broader literature that looks at the regional effects of monetary policy. The heterogeneity in the sensitivity of local economies to interest rates has been documented for the United States (Carlino and DeFina 1998), Europe (Rodriguez-Fuentes and Dow 2003) and Australia (Vespignani 2013). This research typically explores the mechanisms that explain why there are regional differences in sensitivity to monetary policy. The heterogeneity in local responses to monetary policy is typically linked to variation in industrial structure (e.g. share of output due to the manufacturing sector), household demographics (e.g. age structure of the population) or firm dynamics (e.g. firm size). Our results do not suggest these factors are the main drivers behind the regional differences in housing market responses to monetary policy.
Finally, our research is related to the literature that studies the distributional effects of monetary policy (e.g. Doepke, Schneider and Selezneva 2015; Coibion et al 2017). To the best of our knowledge, there has been little research that specifically links monetary policy to housing wealth inequality, which is surprising given the strong relationship between interest rates and housing prices.[6]
2. Theoretical Framework
To develop some empirical predictions, we outline a theoretical framework that explains how monetary policy can affect local housing markets differently and why simple estimates of the local effects of monetary policy might be biased. The framework is based on an asset pricing model used extensively in the finance literature. It is typically referred to as the dynamic Gordon growth model, as applied to the housing market (Hiebert and Sydow 2009).[7] Consider the standard asset pricing formula:
This states that the housing price in the current period (Pt) is equal to the discounted value of the future price of housing (Pt + 1) and current rents (Dt), where the discount rate is equal to R = 1 + r. The discount rate can also be thought of as the ‘required rate of return’, which consists of the risk-free rate plus a risk premium that might vary according to the local housing market. All variables are in real terms. Taking natural logs of this expression:
We would like to obtain a (log) linear relationship between housing prices, rents and discount rates (and ultimately interest rates). But the relationship here is nonlinear as it involves the log of the sum of the future housing price and rents. However, Campbell and Shiller (1988) show that the expression can be approximated as.[8]
Here, the log of the price level (log(Pt)) is approximately equal to a constant (k), the weighted average of the log level of the future housing price and the current rent less the log level of the discount factor (log(Rt)) which is approximately equal to the discount rate.[9] Taking the difference between two consecutive periods, we obtain:
where lower-case letters represent the natural log of the upper-case counterparts represents (quarterly) changes over time and each local housing market is denoted with subscript i. Here, current housing price growth is a function of the change in the discount rate, expected housing price growth in the next period and current rent growth.
We assume that housing investors (including home owners) use market interest rates to discount the future and that, at least for some investors, the relevant discount rate is the short-term cash rate . As such, changes in household discount rates across local housing markets are a function of changes in monetary policy and shocks to local discount rates . The sensitivity of local discount rates to monetary policy varies across local housing markets, as captured by the coefficient .
We similarly assume that local housing price expectations are a function of market interest rates, and that the sensitivity of expectations to monetary policy varies across local markets, as shown by the coefficient :
One possible basis for this variation is that housing supply conditions vary across regions, and both home owners and investors know this, such that they expect local housing price growth to vary across regions in response to aggregate demand shocks, including monetary policy.
Substituting the two expressions, we obtain a regression model that we can explore using local housing market data:
where the sensitivity of local housing price growth to the cash rate is a function of various structural parameters that vary by local housing market and the error term is a function of both local shocks to discount rates and expectations . This simple model indicates that changes in monetary policy can affect current housing prices by influencing either discount rates (through ) or expectations about future housing prices (through ).[10]
The key assumption to pin down the distributional effects of monetary policy on local housing prices is that monetary policy does not respond to local housing shocks . This strategy assumes that there is no aggregate variable, such as GDP growth or unemployment, to which the monetary policy is responding and which has a heterogeneous effect on local housing markets. Suppose that each market has a different sensitivity to changes in aggregate output growth :
where the sensitivity of local housing prices to aggregate output growth is given by the coefficient and is a white noise error. If monetary policy systematically responds to aggregate output growth then the key identification assumption is invalid because . If monetary policy tightens in response to stronger output growth (which drives higher housing prices) this would attentuate the estimates. To account for this bias, we directly control for relevant macroeconomic variables that may have distributional effects on housing prices. We therefore estimate:
Equation (1) forms the basis of our empirical model and is discussed in more detail in Section 4. In Section 6, a version of the model is also estimated using estimates of monetary policy ‘shocks’ that purge the changes in monetary policy of any systematic response to macroeconomic conditions and forecasts.
3. Data
To measure local area housing prices we use data from a private company, CoreLogic. The geographic unit is Statistical Area Level 3 (SA3) (there are 358 SA3s in Australia, with populations varying between 30,000 and 130,000 people). SA3s often align to a regional city (for regional areas) or local government areas like city councils and transport or commercial hubs (for metropolitan areas).
The key variable is a hedonic index for real dwelling prices (this includes prices for detached houses and apartments). The hedonic index captures the change in housing prices controlling for observables such as land size, type of dwelling structure and the number of rooms. It can be thought of as a pure measure of housing prices. The housing price index is deflated by the (trimmed mean) consumer price index to arrive at a real measure.
In the baseline models, the stance of monetary policy is measured by the cash rate target, as published in RBA statistical table F1 (Interest Rates and Yields – Money Market). For the analysis, the sample period spans several housing price cycles covering the three decades between 1990 and 2019. The sample period roughly aligns with the introduction of inflation targeting in Australia, so our analysis should not be affected by changes in monetary policy regimes. For robustness, we also consider estimates of monetary policy shocks, which account for systematic changes in monetary policy by controlling for information that is contained in the Reserve Bank's forecasts (Bishop and Tulip 2017). The monetary policy shock series runs from 1992 to 2018.
The controls for macroeconomic variables such as GDP growth, the terms of trade and the unemployment rate are all sourced from the Australian Bureau of Statistics.[11]
4. Heterogeneity in the Sensitivity of Local Housing Prices to Monetary Policy
4.1 Identification
We estimate Equation (1) using a combination of panel regression techniques and local projections (Jordà 2005). We refer to this as the ‘unrestricted model’:
where:
- is the log difference in the real dwelling price index for region i from quarter t to quarter t + h, where h [1,16] quarters.
- is a region-specific dummy. This controls for time-invariant factors within each local housing market, such as the level of local amenities or distance to the coast. The estimate of this dummy is allowed to change for each horizon h.
- represents the quarterly percentage point change in the cash rate target.
- is a vector of controls for both local and aggregate market conditions.
Equation (2) is estimated separately for each local housing market and at each time horizon. The resulting estimates of the coefficients provide direct estimates of the sensitivity of local housing prices to monetary policy.
The controls include variables that capture macroeconomic conditions, including GDP growth, the terms of trade and the unemployment rate, as well as lagged changes in the cash rate. This addresses concerns that the local housing market sensitivities could be driven by differential sensitivities to aggregate shocks, rather than interest rates per se.
We experimented with including controls for both local housing and labour market conditions, such as rental growth and the local unemployment rate. However, the sample period (and frequency) for which the local level controls are available is somewhat restricted. Over the smaller sample period, the local controls do not meaningfully change the key results.[12]
4.2 Results
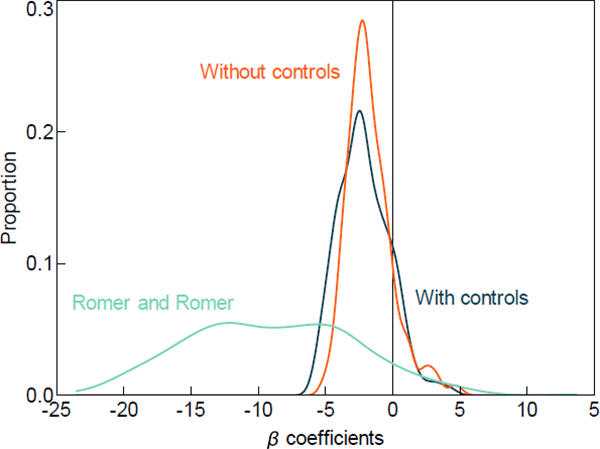
The estimates of the coefficients (at a two-year horizon) for all local areas are plotted as a density in Figure 2. As the density shows, the bulk of the coefficient estimates are negative, implying that housing prices fall in response to tighter monetary policy in most local housing markets. However, as is also clear, there is substantial heterogeneity in the response of local housing prices to changes in monetary policy.
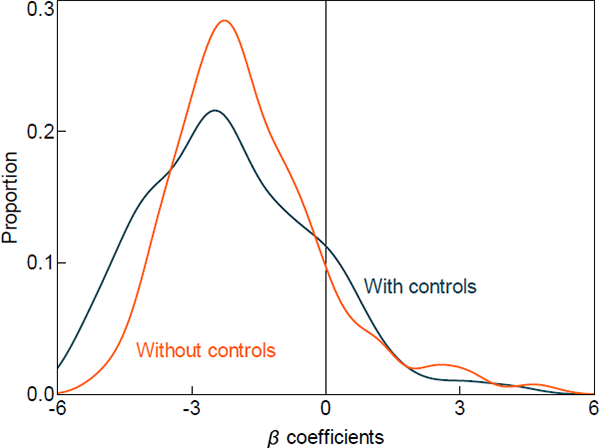
Sources: ABS; Authors' calculations; CoreLogic data; RBA
But how much of this heterogeneity is due to monetary policy per se, and how much is due to the fact that some regions may be more sensitive to aggregate shocks, such as the national business cycle, and monetary policy is responding endogenously to these aggregate shocks? We can examine this by comparing the distributional effects of monetary policy when estimated both with and without controls for macroeconomic conditions. We find that the densities are reasonably similar, though the inclusion of controls for macroeconomic conditions produces slightly more negative responses and ‘flattens’ the distribution (Figure 2). This suggests that some of the heterogeneity across local housing markets is due to varying sensitivity to the business cycle and that the effects of monetary policy on local housing prices are stronger (and more dispersed) when we account for this.
We can also look at how this distribution evolves over time and hence examine the heterogeneity in the dynamics of local housing prices in response to monetary policy (Figure 3). The responses follow a similar pattern and are reasonably close immediately after the change in monetary policy. However, the distribution widens over time. For example, in the median region, housing price falls peak at 2.3 per cent after two years in response to a 100 basis point increase in the cash rate. But at the 25th and 75th percentiles, housing prices fall by 0.9 per cent and 3.5 per cent in response to the same increase in the cash rate.[13] This suggests that the dynamics of housing prices vary substantially across time and local housing markets in response to interest rate changes.
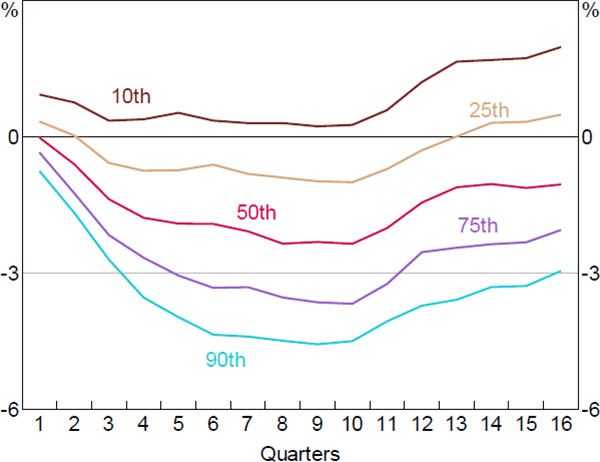
Sources: ABS; Authors' calculations; CoreLogic data; RBA
4.3 Inspecting the Mechanism
Given the wide cross-sectional distribution of housing price responses to monetary policy, we examine factors that might be driving these differences. Guided by the theoretical framework, we consider a range of possible drivers of the link between monetary policy and growth in housing prices, including both housing demand and supply-side factors.
- Housing price expectations: existing research suggests that expectations could play an important role in driving the heterogeneous effects of monetary policy (e.g. Kaplan, Moll and Violante 2018; Ben-David, Towbin and Weber 2019). As such, we consider a range of variables that are likely to be associated with household expectations about future capital gains. This includes the extent to which housing supply is constrained by geography or regulation (Fischer et al 2018; Kendall and Tulip 2018). For instance, expected housing price appreciation may vary by region due to differences in available land supply (Himmelberg et al 2005; Glaeser, Gyourko and Saiz 2008). But we also consider demand-side factors. For example, research indicates that expectations of housing prices are linked to local economic conditions and household demographics, including income (Niu and van Soest 2014). Also, housing investors may have different expectations of capital gains on housing relative to the rest of the population, so we also include estimates of the share of investors in the population.
- Discount rates: there is empirical evidence that discount rates vary across (and even within) individuals (Frederick, Loewenstein and O'Donoghue 2002). So it is plausible that discount rates vary across regions. We consider a range of variables that may be associated with household impatience, and therefore discount rates. Some studies suggest that households that are less patient also have relatively low levels of net wealth (or high levels of debt) (e.g. Carroll et al 2017). Therefore, their discount rates may be relatively sensitive to short-term interest rates, such as the cash rate.[14] It follows that regions that are more indebted may be more sensitive to changes in monetary policy. We proxy for indebtedness across regions based on the share of households with mortgage debt and the share of households that report spending more than 30 per cent of their income on housing costs. More generally, there can be a disconnect between private discount rates and market interest rates because of personal preferences and experiences, including exposure to market instruments (Glaeser, Gottlieb and Gyourko 2012). For example, richer individuals could be more sensitive to changes in market interest rates as changes in market interest rates directly affect their optimal asset allocation.
To assess the relative importance of each factor we take the housing price responses to a 100 basis point increase in the cash rate at an eight-quarter horizon in our unrestricted model ( from Equation (2)) and explore the cross-sectional correlation across regions between the housing price responses and various factors.
where
- is a vector of housing price responses, estimated from Equation (2), for each of 284 local housing markets at an eight-quarter horizon;[15]
- Q represents an n by p matrix of p explanatory variables (including factors associated with housing price expectations, discount rates etc), and represents a p by 1 vector of coefficients;
- is a constant and is a white noise error.
We take two complementary approaches to study these cross-sectional correlations. First, we take a ‘data-driven approach’ and implement some variable selection methods, including elastic net and least angle regression (LAR).[16] We do this given it is difficult to know which variables to include in the determinants of the local housing price responses and we want to avoid overfitting and selection bias. We evaluate over 80 different local area characteristics. Most of the variables are derived from regional data produced by the Australian Bureau of Statistics (ABS) or longitudinal household survey data obtained from the Household, Income and Labour Dynamics in Australia (HILDA) Survey.[17] The optimal model is chosen based on 10-fold cross validation and selecting the maximum penalty (elastic net)/minimum step (LAR) that produces a mean squared error within one standard deviation of the minimum mean squared error.
Second, we take a ‘judgement-based approach’ and examine multivariate OLS regressions for a select number of variables across a range of time horizons.[18] The variables chosen are informed by both theory and the data-driven methods. A ‘general-to-specific’ approach is applied to narrow down the variables to those that were more statistically significant.
The variables selected by the data-driven approach are presented in Table 1.[19] The variables and estimates chosen by the judgement-based approach are presented in Table 2. Based on these two approaches, the factors determining the sensitivity of local housing prices to monetary policy can be loosely tied to the theoretical framework outlined earlier and grouped under the following broad headings:
-
Housing price expectations:
- housing supply conditions (e.g. average price level; share of the value of the home due to land)
- investor density (e.g. share of investors in the population)
-
Discount rates:
- income per capita
- mortgage debt (e.g. share of households with mortgage debt; share of households paying more than 30 per cent of their income on housing costs).
To be clear, this framework provides a useful way of summarising the determinants of the sensitivity of local housing prices to monetary policy. But some variables could fit under either heading. For example, average income may affect both people's expectations about housing prices and their degree of impatience. Similarly, housing investors may have different expectations and discount rates to the broader population.
Table 1: Determinants of Housing Price Responses Selected by all methods – elastic net and LARTheme Elastic net Least angle regression Sensitivity Income Median total income More Median employee income Median employee income More Hand-to-mouth households as a share of working-age population Less Share of individuals claiming low income tax offset(a) Share of individuals claiming low income tax offset(a) Less Share of working-age population earning negative income Less Low income tax offset per capita Less Share of individuals earning
allowances, earnings, tips or
director fees(a)Less Mortgage debt Share of households with high housing servicing costs More Mortgage servicing ratio Mortgage servicing ratio More Housing servicing ratio Housing servicing ratio More Housing supply conditions Average sales price Average sales price More Average price growth Less Investor concentration Rent interest deductions per capita Rent interest deductions per capita More Share of individuals claiming rent
interest deductions(a)Share of individuals claiming rent
interest deductions(a)More Investor density as a share of the working-age population More Investor density as a share of the population More State/territory Victoria Victoria Less Queensland Queensland More Western Australia More Notes: Details about the construction of the various measures are outlined in Appendix A
(a) ‘Share of individuals’ is based on individuals recorded by the ATO based on tax statisticsSources: ABS; Australian Taxation Office; Authors' calculations; CoreLogic data; DSS and Melbourne Institute (2018); RBA
Table 2: Determinants of Housing Price Responses OLS regression estimates at various horizonsVariable Horizon 1-year 2-year 3-year Median sale price (log level, dollars) −0.287
(−0.688)0.077
(0.138)0.524
(0.737)Share of value determined by land (%) −0.012**
(−2.000)−0.011
(−4.880)−0.022**
(−4.642)Rent servicing share (%) 0.029
(0.724)0.043
(0.768)0.153**
(2.155)Mortgage servicing share (%) −0.133***
(−3.339)−0.236***
(−4.880)−0.300***
(−4.642)Mortgagor rate (%) 0.008
(0.806)0.004
(0.286)−0.025
(−1.585)Outright ownership rate (%) 0.033*
(1.824)0.054***
(2.710)0.114***
(4.596)Investor density (%) −0.036**
(−2.432)−0.052***
(−3.300)−0.095***
(−4.944)Employee income (log level, dollars) −2.746**
(−2.138)−3.181*
(−1.723)−0.697
(−0.300)Price growth (percentage change) 0.008***
(3.528)0.012***
(4.215)0.015***
(4.539)R-squared 0.332 0.427 0.414 No of observations 274 274 274 Notes: State dummies for Victoria and Western Australia and constant are omitted from the table; standard errors are robust; *, ** and *** denote statistical significance at the 10, 5 and 1 per cent levels, respectively; t-statistics are in parentheses
Sources: ABS; Australian Taxation Office; Authors' calculations; CoreLogic data; RBA
The results to these two complementary approaches yield a few key findings.
First, both the model selection and OLS results suggest that factors associated with housing supply conditions are important. Specifically, the effect of monetary policy on housing prices is stronger in local housing markets in which supply conditions are tight. For instance, the average sales price is chosen by both selection methods and is likely associated with the availability of housing supply. However, the coefficients are insignificant in the OLS regressions. But when the proportion of housing value determined by land is included in the regressions this points to tighter supply conditions producing larger housing price responses to monetary policy changes.
Second, investors appear to play an important role in housing market dynamics. Specifically, investor-dense regions appear to be more sensitive to changes in monetary policy. The OLS regression estimates indicate that an area with 10 percentage points more investors would experience around a half a percentage point larger fall in housing prices two years after a 100 basis point increase in the cash rate. This may indicate that, relative to the broader population, housing investors have different expectations of capital gains on housing. Alternatively, due to personal preferences, housing investors may have discount rates that are more closely tied to short-term interest rates.
Third, regions with relatively high average incomes display stronger responses to monetary policy. The OLS estimates indicate that a 1 percentage point increase in income is associated with a 3.2 basis points larger negative response of housing prices two years after a percentage point increase in the cash rate. This suggests that high income areas are more sensitive to monetary policy because their discount rates are more closely tied to market interest rates (Glaeser et al 2012).[20] Alternatively, because average incomes are likely to be correlated with the value of local amenities, it may be that areas with relatively high average incomes are those in which housing supply is tight (and these supply conditions are not fully captured by the average housing price level).
Fourth, there is some evidence that, in more indebted regions, housing prices are more sensitive to changes in interest rates. The model selection methods find that areas with relatively high housing costs (either mortgage payments or rents) are more responsive to monetary policy. In addition, the OLS model suggests that these results are driven by high mortgage servicing ratios, as opposed to rental payments.
Lastly, we find evidence that the housing markets in Western Australia (more sensitive) and Victoria (less sensitive) have systematically different responses to monetary policy compared to other states and territories. This may reflect how monetary policy responds to activity in different states. In particular, the Reserve Bank focuses on aggregate measures of economic activity and inflation in setting monetary policy. For example, monetary policy may be less sensitive to activity in Western Australia as its business cycle could be tied to factors that are unrepresentative for the rest of Australia, such as global demand for commodities. Conversely, monetary policy could be more sensitive to activity in Victoria where the business cycle is more representative of the aggregate business cycle. This response could drive systematically different responses of housing prices to monetary policy across states. Specifically, when economic activity is high in Victoria this likely corresponds to increasing housing prices in Victoria. And if monetary policy were to tighten in response to this economic activity it would serve to curb the housing price movements in Victoria; resulting in more muted housing price responses. At the same time, if Western Australia's economy and housing market were weaker, the change in monetary policy could have a larger effect on the Western Australian housing cycle. That is, monetary policy could offset housing cycles in one state or territory and amplify them in another.
These variables are not an exhaustive list of possible determinants. Indeed, the R-squared on these regressions range from 33 to 43 per cent, suggesting that the OLS models do not fully capture the variation in housing price responses. It is possible that the local housing price sensitivities depend on factors in a nonlinear fashion (e.g. interactions between debt and income). Such nonlinear effects have not been considered. Moreover, the results are not necessarily causal (e.g. because the level of mortgage debt depends on past changes in monetary policy). And the results are quite sensitive to the choice of variables, the time horizon and the controls that are included in the baseline regression. But the results do indicate that housing supply conditions are not the only factor that matters to the sensitivity of local housing prices.[21]
5. The Distributional Effects of Monetary Policy on Housing Wealth
5.1 Identification
Next, we estimate a version of the model where the focus is on the heterogeneity in price levels across local housing markets. This version of the model directly tells us about the link between monetary policy and inequality in housing wealth. For example, if changes in monetary policy affect prices in expensive areas by more than in cheap areas, this would suggest that monetary policy affects housing wealth inequality.
For this exercise, we adopt an alternative approach to the unrestricted model to control for macroeconomic conditions. Specifically, time fixed effects are included in the model and the focus is solely on the differences in sensitivity to monetary policy across local housing markets. If we estimate Equation (1) as it stands and include time fixed effects then we will not be able to separately identify the effect of monetary policy , as it only varies with time and hence is not linearly independent:
But we can still identify differences (from some baseline) in the sensitivity to monetary policy across regions. To see this, suppose we have just two local housing markets, A and B, where region A is more expensive on average than region B. We are interested in identifying whether more expensive regions are more sensitive to monetary policy than less expensive regions. While we cannot estimate the equation above, we can estimate this:
where D is a dummy variable that is equal to one if the region is A and zero if the region is B. The estimates of the time fixed effects will set the baseline (in this case, region B) and the estimate of will capture the difference between regions A and B in their sensitivity to monetary policy. We can then test whether monetary policy has a different effect on housing price growth depending on how expensive the region is.
As before, we also need to account for the fact that macroeconomic conditions can have differential effects on local housing markets, and it may be that monetary policy is endogenously responding to these changes in the economy. So, similar to before, we include controls for macroeconomic conditions and interact them with the dummy variable to control for these differential effects:
The local housing markets are divided into price deciles depending on how expensive they are. To do this we group regions based on their ‘initial’ housing price level. We divide SA3 regions into price deciles based on the average sale price between 1991 and 1994. We set each local housing market to remain in the same decile over the sample period. This is to prevent endogenous changes in price groups driven by monetary policy. This choice is supported by the data. Between the early 1990s and 2019, only 6 per cent of local housing markets moved more than two price deciles. The persistence of these gaps in pricing suggest that housing price differences are at least in part determined by longer-term supply conditions, such as geographic or zoning constraints. (Gyourko, Mayer and Sinai 2013).
We also impose the restriction that local housing markets in the same price decile respond similarly to monetary policy . We refer to this as the ‘restricted model’:
where all the notation is as before, but now we also have an indicator variable equal to one if region i belongs to national price decile g = 1,…,10 (Decileg). The set of coefficients represents the effect of cash rate changes on housing prices h periods ahead for each decile g, after controlling for changes in macroeconomic conditions (included in the control variables Xt) The housing market groupings non-parametrically allow different deciles to have different responses to monetary policy. Adding time fixed effects to the model and removing the 5th decile (i.e. the 40th to 50th percentile) makes the 5th decile our benchmark (denoted by subscript b). The use of the benchmark modifies the interpretation of the coefficients . These coefficients represent the difference in the housing price response of decile g relative to the price response of the 5th decile. In the baseline model, we include four lags of the change in the cash rate as well as controls for year-ended growth in GDP, the terms of trade and the unemployment rate. We also allow these controls to have differential effects on the price deciles by interacting them with the dummy variables for each price decile.
5.2 Results
The estimated coefficients of the restricted model are presented in Figure 4. Recall that this model estimates the differential effect of monetary policy between price deciles and the median group (the 5th decile). The results suggest that monetary policy has heterogeneous effects across the distribution of price levels. Specifically, following an increase in the cash rate, housing prices in more expensive housing markets (the upper deciles) fall more strongly than prices in cheaper markets (the lower deciles).
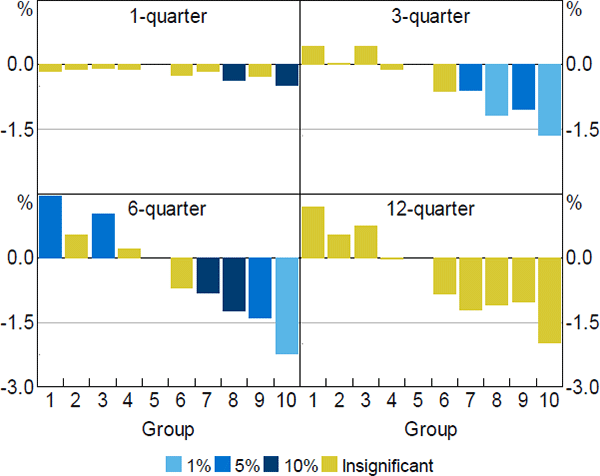
Note: Colours represent level of significance of estimated coefficients using standard errors clustered across time and state (or territory)
Sources: ABS; Authors' calculations; CoreLogic data; RBA
The largest differences in response to monetary policy changes occur in the top half of the price distribution. We find that a 100 basis point increase in the cash rate is associated with housing prices falling by more in the expensive areas after about three quarters. The peak difference in housing price responses occurs six quarters following the change in monetary policy at about –1.4 per cent, on average. This implies, for example, that housing prices would fall by about 3.7 per cent in the top four price deciles if prices in the median area fall by 2.3 per cent in response to a 100 basis point increase in the cash rate. In the bottom half of the price distribution, local areas appear to be less sensitive to changes in the cash rate than the median area, though the evidence is less clear.
The differential effects of monetary policy changes on housing prices appear to be temporary. The differences across all price deciles becomes statistically insignificant beyond two years. These spatial deviations in prices are indicative of housing market frictions, as price differentials should not be observed in efficient markets. These frictions could reflect transaction costs, home bias of buyers or asymmetric information. However, the temporary nature of the price differentials suggest that the frictions dissipate over time.[22]
5.3 Housing Supply Factors
So why are more expensive areas more sensitive to monetary policy? A possible explanation is that more expensive areas are more constrained in terms of new housing supply. In the long-run, housing prices should move in line with construction costs. But there is evidence of systematic short-run deviations, which suggests that land availability matters (Himmelberg et al 2005).
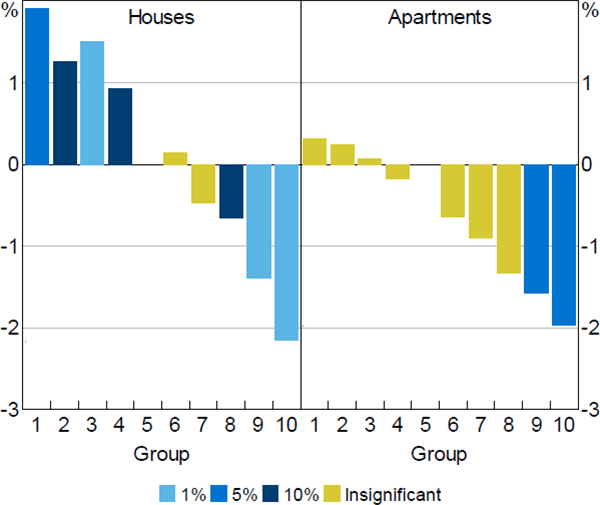
We test this hypothesis by separately estimating the effect of monetary policy on the price distribution of detached homes and apartments across local areas. Detached houses are naturally more sensitive to changes in land value than apartments, as land represents a larger proportion of the value of detached houses (Kendall and Tulip 2018). So, if land availability matters, then monetary policy should be able to affect the price distribution of detached houses more than the price distribution of apartments. In our asset pricing model, this would be represented through a more negative value of for detached houses than apartments.
To estimate these models, we redefine the price deciles for houses and apartments separately. This allows us to directly answer if monetary policy alters the price distribution of houses or apartments.[23] Our results provide some weak evidence for the ‘land availability hypothesis’. We find that the price distribution of detached houses are slightly more sensitive than apartments to cash rate changes (Figure 5). Here, in response to a 100 basis point increase in cash rate, the peak difference between the most expensive 30 per cent of areas and the median group for detached houses and apartments is on average −1.2 and −1.5 percentage points, respectively. The key difference between the responses of houses and apartments occurs at the lower end of the price distribution. For detached houses, areas in the cheapest 30 per cent of areas experience a differential response to the median group of around 1.6 percentage points. These effects are statistically significant. However, for apartments in price groups below the median, the differences in price response to changes in monetary policy relative to the median group are small and statistically insignificant. This provides some evidence to suggest that changes in monetary policy do not meaningfully alter the distribution of apartment prices across regions.
Evaluating the estimates jointly, we find that the differences between the estimates for houses and apartments are not statistically different from one another. Moreover, it is difficult to determine if these effects are confounded by the degree of substitutability between apartments and houses. For example, increases in house prices may spillover into the apartments if the demand to own housing is inelastic. Overall, we view these results as weak evidence to land availability driving the heterogeneous response of housing prices across the distribution of housing wealth.
Note: Colours represent level of significance of estimated coefficients using standard errors clustered across time and state (or territory)
Sources: ABS; Authors' calculations; CoreLogic data; RBA
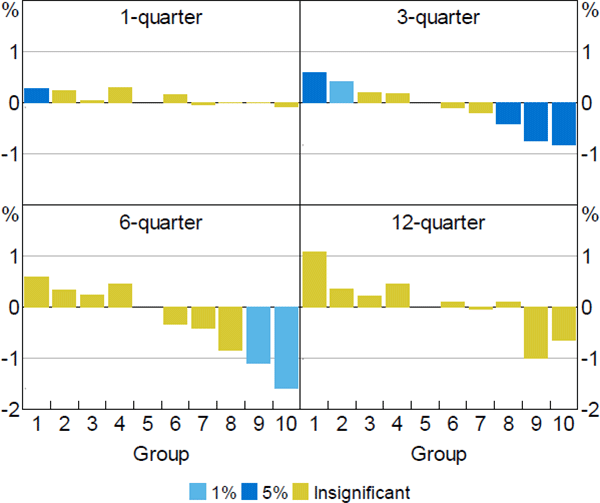
An alternative approach to capture the role of land is to disentangle the land value from the cost of the structure following the methodology of Kendall and Tulip (2018).[24] Specifically, for each local area, we estimate a hedonic regression on home sale unit record data. We then calculate the physical land component of a dwelling by taking the average sales price and multiplying it by the estimated coefficient of land on price (i.e. elasticity of price to land). The local areas can then be divided into deciles based on the share of the sales price that is accounted for by the physical land component. And then we can re-estimate the restricted model using these new groupings and explore the variation across local areas based on the value of physical land.
The deciles using this measure of value determined by land differ from the baseline specification that divides areas by average sales price from the early 1990s. The correlation between the measure of proportion of value determined by land in an area and average sales price is 0.41, suggesting that there is some overlap between the groupings but enough difference to be indicative if the land availability hypothesis is a valid explanation to the differentials generated in our baseline restricted model.
Doing so, we find that housing prices are more sensitive to the cash rate in areas where land is valuable (Figure 6). Specifically, following a 100 basis point increase in the cash rate, the top two deciles experience a larger fall in housing prices relative to then benchmark group. This effect peaks at around –1.34 per cent, six quarters following the change in the cash rate. These effect sizes and timings are comparable to our baseline restricted model estimates. These results are consistent with land availability being an important driver of the heterogeneity in sensitivity to monetary policy across housing price levels.[25]
Note: Colours represent level of significance of estimated coefficients using standard errors clustered across time and state (or territory)
Sources: ABS; Authors' calculations; CoreLogic data; RBA
Overall, we find some evidence to suggest that land availability plays some role in driving the heterogeneous response of housing prices across price deciles. However, the results comparing apartment and housing prices suggest other factors could also be important. This is consistent with the previous section that found a variety of factors related to both supply and demand are important in explaining the distribution of responses of housing prices across all local areas.
6. Robustness Tests
6.1 Alternative Measures of Monetary Policy
We re-estimate the unrestricted model but replace the cash rate with a plausibly exogenous measure of monetary policy. Following Romer and Romer (2004), we estimate a series of monetary policy ‘shocks’. Unlike our baseline models, these shocks attempt to isolate the unexpected component of monetary policy changes.
This monetary policy shock series is constructed by purging changes in the cash rate of information in the Reserve Bank's forecasts of unemployment, real GDP and inflation (Bishop and Tulip 2017). Following Beckers (2020), this shock measure is extended to also account for credit spreads and we also include an autoregressive (AR(1)) forecast of housing prices. We include credit spreads as they appear to have predictive power over and above the Reserve Bank's forecasts in forecasting cash rate changes. Moreover, accounting for an AR(1) forecast of housing prices explicitly models any response in the cash rate to housing price information.[26]
Where:
- is the quarterly change in the cash rate;
- is the quarterly lag of the cash rate level;
- represents the Reserve Bank's forecasts and forecast revisions of real GDP, inflation and unemployment (two-quarters-ahead);
- CSt is a measure of credit spreads used in Beckers (2020), including: the spread between the 3-month bank-accepted bill (BAB) rate and the 3-month Australian dollar overnight indexed swap (OIS), the spread between the average large business variable lending rate and the 3-month BAB rate, and the US BAA 10-year spread;
- is an AR(1) forecast and forecast revisions of real housing prices (two-quarters-ahead).
The estimated residuals represent monetary policy shocks (or deviations from a forward-looking monetary policy rule). Substituting the monetary policy shocks in place for cash rate changes gives us the following equation:
where is the estimated effect of monetary policy on housing prices for region i.
Using this alternate measure of monetary policy in the unrestricted model produces quite a different distribution of housing price responses. Figure 7 compares the distribution of responses using the Romer and Romer-style shocks against the cash rate changes. The results suggest that two years after a 100 basis point increase in monetary policy the median area experiences a 9 percentage point decline in housing prices, while the 25th and 75th percentiles experience declines of 4 per cent and 14 per cent, respectively. The centre of the distribution differs, and the variance of the distribution is clearly larger. This provides further evidence that monetary policy has strong distributional effects across local housing markets. And it may suggest that there are other unobserved factors that drive both changes in monetary policy and heterogeneous effects across local housing markets that are not well captured by the controls for macroeconomic conditions. However, we believe that mismeasurement is also an issue with these shocks as demonstrated by the greater uncertainty around the estimates.
Sources: ABS; Authors' calculations; CoreLogic data; RBA
6.2 Alternative Measures of Local Housing Markets
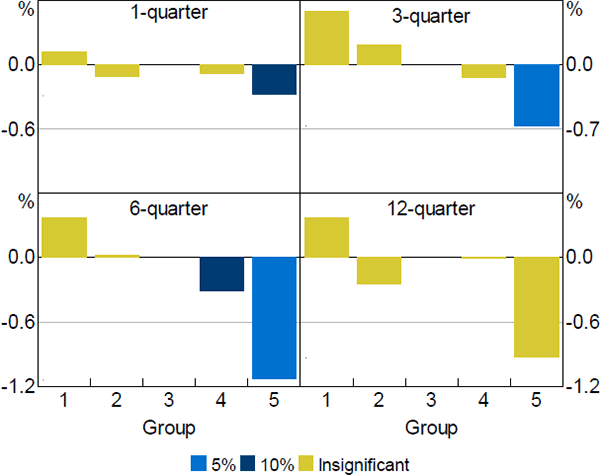
It may be the case that the results from the restricted model are affected by the differences between metropolitan and regional local housing markets. To explore whether metropolitan and regional areas display different levels of heterogeneity, we re-estimate the restricted model using only the sample of metro areas. By removing areas outside of the greater capital cities, the sample of local housing markets is reduced to 156. We divide these metro areas into price quintiles to account for the smaller number of areas.
The results suggest that the variation in housing price responses across local housing markets is only partially explained by differences between regional and metro areas (Figure 8). Even within metro areas, in response to an increase in the cash rate more expensive markets experience larger falls in housing prices relative to the median. This is consistent with the earlier observation that, even within states, housing price growth can vary substantially.
Notes: Colours represent level of significance of estimated coefficients using standard errors clustered across time and state (or territory); price quintiles are calculated using only metropolitan areas
Sources: ABS; Authors' calculations; CoreLogic data; RBA
7. Conclusion
We document a wide distribution in the effect of monetary policy across local housing markets. Looking into this distribution, we find evidence that these differences in local housing price responses to monetary policy are partially explained by factors such as housing supply conditions, mortgage debt, investor concentration and average income. This speaks to the underlying transmission of monetary policy and suggests that the effectiveness of monetary policy through the housing market is dependent on the state of the economy. Specifically, monetary policy could have larger effects on housing prices when supply constraints are binding, mortgage debt is higher, there are more investors and incomes are higher, all other things being equal. And while the estimates are not causal in nature, the results do suggest that it is important to account for a wide range of factors when analysing the effects of monetary policy on housing market dynamics.
We also explore how monetary policy effects the distribution of housing wealth. Our results show that housing prices in the most expensive areas are the most sensitive to interest rate changes, indicating that monetary policy can change the distribution of housing wealth. We find some evidence that the available supply of land partly explains this result. Our results also suggest that the distributional effects on housing wealth are temporary, with the effects of monetary policy across the price distribution converging over time.
Appendix A: Data Description
| Variable | Source | Start date | End date | Frequency |
|---|---|---|---|---|
| Hedonic dwelling price index | CoreLogic | March 1990 | June 2019 | Quarterly |
| Hedonic house price index | CoreLogic | March 1990 | June 2019 | Quarterly |
| Hedonic apartment price index | CoreLogic | March 1990 | June 2019 | Quarterly |
| Median sales price | CoreLogic | March 1990 | June 2019 | Quarterly |
| Cash rate target | RBA | March 1990 | June 2019 | Quarterly |
| GDP growth, year-ended | ABS | March 1990 | June 2019 | Quarterly |
| Unemployment rate | ABS | March 1990 | June 2019 | Quarterly |
| Terms of trade | ABS | March 1990 | June 2019 | Quarterly |
| RBA forecasts of unemployment, real GDP and inflation | RBA | September 1992 | September 2018 | Quarterly |
| Forecast of aggregate real housing index | CoreLogic, ABS and authors' calculations | September 1992 | September 2018 | Quarterly |
| Credit measure spreads | Beckers (2020) | September 1992 | September 2018 | Quarterly |
| Variable | Description | Source | Year |
|---|---|---|---|
| Population density | Population per square metre | ABS Census, Australian Statistical Geography Standard (ASGS) |
1991, 2016 |
| Dwelling density | Number of dwellings per square metre | ABS Census, ASGS | 1991, 2016 |
| Median age | ABS Census | 2016 | |
| Mortgagor rate | Share of dwellings owned with a mortgage; per cent | ABS Census | 2016 |
| Ownership rate | Share of dwellings owned with a mortgage or outright; per cent | ABS Census | 2016 |
| Outright ownership rate | Share of dwellings owned outright; per cent | ABS Census | 2016 |
| Renter rate | Share of dwellings rented; per cent | ABS Census | 2016 |
| Share of workers in mining, manufacturing or financial industry | Share of working-age population; per cent | ABS Census | 2016 |
| Share of workers in ‘cyclical’ industries | Share of working-age population in construction, accommodation, and food or retail trade; per cent | ABS Census | 2016 |
| Apartment share | Share of dwellings that are apartments; per cent | ABS Census | 2016 |
| Income growth | Percentage points | ABS Census | 2006, 2011, 2016 |
| Share rent interest deductions(a) | Share of individuals with rent interest deductions; per cent | ATO | 2016/17 |
| Rent interest deductions per capita | Log level (dollars) | ATO | 2016/17 |
| Share of individuals with rental income(a) |
Per cent | ATO | 2016/17 |
| Rental profit per capita | Log level (dollars) | ATO | 2016/17 |
| Share of individuals with interest income(a) |
Per cent | ATO | 2016/17 |
| Share of individuals with net capital gains(a) |
Per cent | ATO | 2016/17 |
| Net capital gains per capita | Log level (dollars) | ATO | 2016/17 |
| Share of individuals with unfranked dividends(a) |
Per cent | ATO | 2016/17 |
| Share of individuals with franked dividends(a) |
Per cent | ATO | 2016/17 |
| Share of individuals with franked dividend credits(a) |
Per cent | ATO | 2016/17 |
| Share of individuals with dividend deductions(a) |
Per cent | ATO | 2016/17 |
| Unfranked dividends per capita | Log level (dollars) | ATO | 2016/17 |
| Franked dividends per capita | Log level (dollars) | ATO | 2016/17 |
| Franked dividend credits per capita | Log level (dollars) | ATO | 2016/17 |
| Dividend deductions per capita | Log level (dollars) | ATO | 2016/17 |
| Share of individuals with salary or wages(a) |
Per cent | ATO | 2016/17 |
| Salary or wage per capita | Log level (dollars) | ATO | 2016/17 |
| Taxable income per capita | Log level (dollars) | ATO | 2016/17 |
| Share of individuals with low income tax offset(a) |
Per cent | ATO | 2016/17 |
| Low income tax offset per capita | Log level (dollars) | ATO | 2016/17 |
| Share of individuals with allowance, earnings, tips, director fees(a) | Per cent | ATO | 2016/17 |
| Allowance, earnings, tips, director fees per capita | Log level (dollars) | ATO | 2016/17 |
| Median investment income | Log level (dollars) | ABS | 2016 |
| Mean investment income | Log level (dollars) | ABS | 2016 |
| Median employee income | Log level (dollars) | ABS | 2016 |
| Median total income excluding government pensions | Log level (dollars) | ABS | 2016 |
| Share of working-age population earning negative income per week | Per cent | ABS | 2016 |
| Share of working-age population earning no income per week | Per cent | ABS | 2016 |
| Share of working-age population earning between $1–$499 per week | Per cent | ABS | 2016 |
| Share of working-age population earning between $500–$999 per week | Per cent | ABS | 2016 |
| High mortgage servicing | Share of households with mortgage repayments greater than or equal to 30 per cent of household income | ABS | 2016 |
| High rent servicing | Share of households with rental payments greater than or equal to 30 per cent of household income | ABS | 2016 |
| Share of population on age pension | Per cent | ABS | 2018 |
| Household net worth | Log level (dollars) | ABS | 2016 |
| Share of hand-to-mouth households | As defined by La Cava, Hughson and Kaplan (2016); per cent | HILDA | 2002, 2006, 2010, 2014 |
| Share of wealthy hand-to-mouth households | As defined by La Cava et al (2016); per cent | HILDA | 2002, 2006, 2010, 2014 |
| Share of poor hand-to-mouth households | As defined by La Cava et al (2016); per cent | HILDA | 2002, 2006, 2010, 2014 |
| Mean net worth | Log level (dollars) | HILDA | 2002, 2006, 2010, 2014 |
| Mean liquid wealth | Log level (dollars) | HILDA | 2002, 2006, 2010, 2014 |
| Mean illiquid wealth | Log level (dollars) | HILDA | 2002, 2006, 2010, 2014 |
| Share of housing value determined by ‘zoning’ | See Appendix B for details; per cent | CoreLogic; RBA | 2015–16 |
| Share of housing value determined by land | See Appendix B for details; per cent | CoreLogic; RBA | 2015–16 |
| Share of housing value determined by physical land | See Appendix B for details; per cent | CoreLogic; RBA | 2015–16 |
| Share of housing value determined by structure | See Appendix B for details; per cent | CoreLogic; RBA | 2015–16 |
| Mortgage servicing share | Median mortgage payment as a percentage of median household income; per cent | ABS Census | 2016 |
| Rent servicing share | Median rent payment as a percentage of median household income; per cent | ABS Census | 2016 |
| Housing servicing share | Weighted average of mortgage and rent servicing ratios; weighted by share of households with mortgages or are renters | ABS Census | 2016 |
| Investor density (working-age population) | Share of working-age population with investment income; per cent | ABS Census | 2016 |
| Investor density (population) | Share of population with investment income; per cent | ABS Census | 2016 |
| Investment-to-total income ratio | Median investment income divided by median total income excluding government pensions | ABS Census | 2016 |
| Share on government benefits | Share of working-age population that receive Newstart or parenting payments | ABS Census | 2016 |
| Share of working-age population earning at or below $999 per week | Per cent | ABS Census | 2016 |
| Average unemployment rate | Per cent | ABS | 2010–18 |
| Median household income | Log level (dollars) | ABS Census | 1991 |
| Median individual income | Log level (dollars) | ABS Census | 1991 |
| Unemployment rate | Per cent | ABS Census | 1991 |
| Employment-to-working-age population rate | Per cent | ABS Census | 1991 |
| Rental growth | Percentage points | CoreLogic | 2005–18 |
| Average sales growth | Log level (dollars) | CoreLogic | 1991–94 |
| Housing price growth | Growth in hedonic dwelling price index; percentage change | CoreLogic | 1994–19 |
|
Notes: State and territory indicators of SA3s are also included in the elastic net and LAR (a) ‘Share of individuals’ is based on individuals recorded by the ATO based on tax statistics |
|||
Appendix B: Kendall and Tulip
To determine the proportion of value determined by land (physical land – the marginal value of land – and ‘zoning’ effects) in an area, we estimate a hedonic index for each local area (SA3) and impute the proportion of value that can be attributed to structure and land. This approach is the same used in Kendall and Tulip (2018). It assumes that the value of a property can be broken into a land component and a structure component.
The Land component can be further decomposed into a physical land and zoning effect component.
Using the same unit record data from CoreLogic on housing sales, we take all housing sales that meet the following criteria:
- sold in 2015 or 2016; we do not use sales in the early 1990s due to data limitations in building approvals
- land area less than 8093.7 square metres; as used in Kendall and Tulip (2018)
- for the period and SA3 region, the property is not below the 1st percentile or above the 99th percentile in sales price or land area.
For each SA3 area we run the following regression:
where j represents a dwelling in suburb s within an SA3; represent time fixed effects; and represent suburb fixed effects.
To determine the value of structure for each region we impute the average real cost per square metre of houses from building approvals data over the ten years to 2016. These data are sourced from the ABS building approvals data. For areas where more than half the houses sold were built on or before 1950, we again follow Kendall and Tulip (2018) and add a 40 per cent premium to the calculated structure value to account for differentials in the value of various period houses relative to modern houses.
The land component of an area's housing value is determined by the mean sales price minus the calculated value of structure for the area
The value of the physical component of land determined by the structure is the mean sales price multiplied by from Equation (B1). The value of land attributed to ‘zoning’ is the residual value of land not attributed to the physical component.
The proportions are obtained by dividing each component by the mean sales price. We include all proportions in the model selection procedures of Section 4.3. And we only use the proportion of the physical land in Section 5.3, as we find that this variable is significant in our regressions in Table 2.
Appendix C: Rolling Samples
To assess the stability of our estimates we conduct rolling regressions. We re-estimate our baseline model taking 15-year samples from 1990 to 2019. Our full-sample results are robust to this change.
Figure C1 shows the six-quarter-ahead housing price responses using different sub-samples of the data. The earliest sub-sample (1990:Q1–2005:Q2) shows similar results to our baseline; more expensive regions respond more to changes in monetary policy than the median group. However, the magnitudes are slightly larger with the average of the top four deciles being –2.23 percentage points. The latest sub-sample (2004:Q3–2019:Q3) provides some evidence to suggest that the distributional effects of monetary policy on housing wealth has become weaker over time, with more expensive areas experiencing similar housing price responses to the median group. However, the differences between the estimates across sub-samples are not statistically distinguishable from one another.
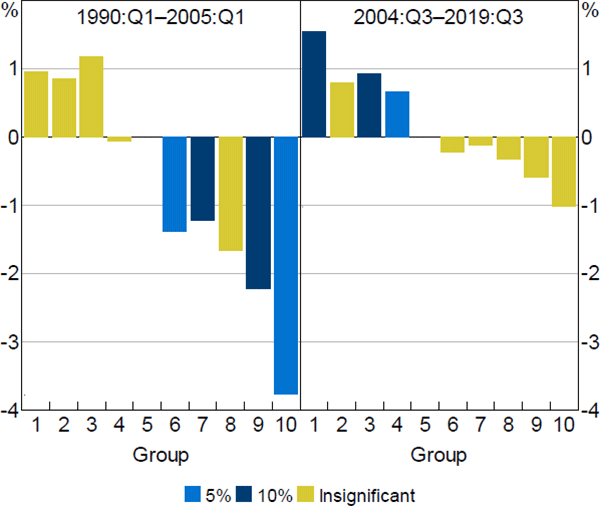
Note: Colours represent level of significance of estimated coefficients using standard errors clustered across time and state (or territory)
Sources: ABS; Authors' calculations; CoreLogic data; RBA
References
Aastveit KA and AK Anundsen (2016), ‘House Prices, Monetary Policy and Regional Heterogeneity’, Unpublished manuscript, Norges Bank, April.
Beckers B (2020), ‘Credit Spreads, Monetary Policy and the Price Puzzle’, RBA Research Discussion Paper No 2020-01.
Ben-David I, P Towbin and S Weber (2019), ‘Expectations during the U.S. Housing Boom: Inferring Beliefs from Actions’, NBER Working Paper No 25702, rev November 2019.
Beraja M, A Fuster, E Hurst and J Vavra (2019), ‘Regional Heterogeneity and the Refinancing Channel of Monetary Policy’, The Quarterly Journal of Economics, 134(1), pp 109–183.
Bishop J and P Tulip (2017), ‘Anticipatory Monetary Policy and the “Price Puzzle”’, RBA Research Discussion Paper No 2017-02.
Campbell JY and RJ Shiller (1988), ‘Stock Prices, Earnings, and Expected Dividends’, The Journal of Finance, 43(3), pp 661–676.
Carlino G and R DeFina (1998), ‘The Differential Regional Effects of Monetary Policy’, The Review of Economics and Statistics, 80(4), pp 572–587.
Carroll C, J Slacalek, K Tokuoka and MN White (2017), ‘The Distribution of Wealth and the Marginal Propensity to Consume’, Quantitative Economics, 8(3), pp 977–1020.
Coibion O, Y Gorodnichenko, L Kueng and J Silvia (2017), ‘Innocent Bystanders? Monetary Policy and Inequality’, Journal of Monetary Economics, 88, pp 70–89.
Colciago A, A Samarina and J de Haan (2019), ‘Central Bank Policies and Income and Wealth Inequality: A Survey’, Journal of Economic Surveys, 33(4), pp 1199–1231.
Cooper D, MJ Luengo-Prado and G Olivei (2016), ‘Monetary Policy and Regional House-Price Appreciation’, Federal Reserve Bank of Boston Research Department Working Papers No 16-18.
Del Negro M and C Otrok (2007), ‘99 Luftballons: Monetary Policy and the House Price Boom across U.S. States’, Journal of Monetary Economics, 54(7), pp 1962–1985.
Doepke M, M Schneider and V Selezneva (2015), ‘Distributional Effects of Monetary Policy’, Paper presented at the Society of Economic Dynamics 2015 Annual Meeting, Warsaw, 25–27 June.
Dokko J, BM Doyle, MT Kiley, J Kim, S Sherlund, J Sim, S Van Den Heuvel and J-P L'Huillier and F Perri (2011), ‘Monetary Policy and the Global Housing Bubble’, Economic Policy, 26(66), pp 237–287.
DSS and Melbourne Institute (Department of Social Services and Melbourne Institute of Applied Economic and Social Research) (2018), ‘The Household, Income and Labour Dynamics in Australia (HILDA) Survey, RESTRICTED RELEASE 17 (Waves 1-17)’, ADA Dataverse, V2, accessed 27 June 2019. Available at <doi:10.26193/OFRKRH>.
Fischer MM, F Huber, M Pfarrhofer and P Staufer-Steinnocher (2018), ‘The Dynamic Impact of Monetary Policy on Regional Housing Prices in the United States’, University of Salzburg Working Papers in Economics No 2018-07.
Fox R and P Tulip (2014), ‘Is Housing Overvalued?’, RBA Research Discussion Paper No 2014-06.
Frederick S, G Loewenstein and T O'Donoghue (2002), ‘Time Discounting and Time Preference: A Critical Review’, Journal of Economic Literature, 40(2), pp 351–401.
Gibbs CG, J Hambur and G Nodari (2018), ‘DSGE Reno: Adding a Housing Block to a Small Open Economy Model’, RBA Research Discussion Paper No 2018-04.
Glaeser EL, JD Gottlieb and J Gyourko (2012), ‘Can Cheap Credit Explain the Housing Boom?’, in EL Glaeser and T Sinai (eds), Housing and the Financial Crisis, National Bureau of Economic Research Conference Report, University of Chicago Press, Chicago, pp 301–359.
Glaeser EL, J Gyourko and A Saiz (2008), ‘Housing Supply and Housing Bubbles’, Journal of Urban Economics, 64(2), pp 198–217.
Glaeser EL, J Gyourko and RE Saks (2006), ‘Urban Growth and Housing Supply’, Journal of Economic Geography, 6(1), pp 71–89.
Gyourko J, C Mayer and T Sinai (2013), ‘Superstar Cities’, American Economic Journal: Economic Policy, 5(4), pp 167–199.
Hastie T, R Tibshirani and J Friedman (2009), The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd edn, Springer Series in Statistics, Springer, New York.
Hiebert P and M Sydow (2009), ‘What Drives Returns to Euro Area Housing? Evidence from a Dynamic Dividend-Discount Model’, European Central Bank Working Paper Series No 1019.
Himmelberg C, C Mayer and T Sinai (2005), ‘Assessing High House Prices: Bubbles, Fundamentals and Misperceptions’, Journal of Economic Perspectives, 19(4), pp 67–92.
Jordà Ò(2005), ‘Estimation and Inference of Impulse Responses by Local Projections’, The American Economic Review, 95(1), pp 161–182.
Jordà Ò, M Schularick and AM Taylor (2015), ‘Betting the House’, Journal of International Economics, 96(Supplement 1), pp S2–S18.
Kaplan G, K Mitman and GL Violante (2019), ‘The Housing Boom and Bust: Model Meets Evidence’, Unpublished manuscript, September. Available at <https://static1.squarespace.com/static/5d69437d65a29d0001ae6520/t/5daa58e5a6cdd33e2a9060e4/1571444967065/kaplan_mitman_violante_sep2019.pdf>.
Kaplan G, B Moll and GL Violante (2018), ‘Monetary Policy According to HANK’, The American Economic Review, 108(3), pp 697–743.
Kendall R and P Tulip (2018), ‘The Effect of Zoning on Housing Prices’, RBA Research Discussion Paper No 2018-03.
Kiyotaki N, A Michaelides and K Nikolov (2011), ‘Winners and Losers in Housing Markets’, Journal of Money, Credit and Banking, 43(2-3), pp 255–296.
La Cava G, H Hughson and G Kaplan (2016), ‘The Household Cash Flow Channel of Monetary Policy’, RBA Research Discussion Paper No 2016-12.
Lim GC and S Tsiaplias (2018), ‘Interest Rates, Local Housing Markets and House Price Over-Reactions’, Economic Record, 94(S1), pp 33–38.
Lowe P (2019), ‘The Housing Market and the Economy’, Keynote address to the Australia Financial Review Business Summit ‘Trust, Purpose and Prosperity’, Sydney, 5–6 March.
Niu G and A van Soest (2014), ‘House Price Expectations’, Institute for the Study of Labor, IZA Discussion Paper No 8536.
Otto G (2007), ‘The Growth of House Prices in Australian Capital Cities: What Do Economic Fundamentals Explain?’, The Australian Economic Review, 40(3), pp 225–238.
Rodriguez-Fuentes C and S Dow (2003), ‘EMU and the Regional Impact of Monetary Policy’, Regional Studies, 37(9), pp 969–980.
Romer CD and DH Romer (2004), ‘A New Measure of Monetary Shocks: Derivation and Implications’, The American Economic Review, 94(4), pp 1055–1084.
Saiz A (2010), ‘The Geographic Determinants of Housing Supply’, The Quarterly Journal of Economics, 125(3), pp 1253–1296.
Saunders T and P Tulip (2019), ‘A Model of the Australian Housing Market’, RBA Research Discussion Paper No 2019-01.
Vespignani JL (2013), ‘The Industrial Impact of Monetary Shocks during the Inflation-Targeting Era in Australia’, Australian Economic History Review, 53(1), pp 47–71.
Williams JC (2016), ‘Measuring the Effects of Monetary Policy on House Prices and the Economy’, in Expanding the Boundaries of Monetary Policy in Asia and the Pacific, Proceedings of a Conference held on 19–21 August 2015 in Jakarta, Indonesia and co-hosted by Bank Indonesia and the Bank for International Settlements, BIS Papers No 88, Bank for International Settlements, Basel, pp 7–16.
Wong A (2019), ‘Refinancing and the Transmission of Monetary Policy to Consumption’, Unpublished manuscript, Princeton University, May. Available at <https://static1.squarespace.com/static/576576adbe659449f97e0d35/t/5ce1f9f23fdc1e00014f3d22/1558313459256/Paper_AERrevision_0519.pdf>.
Copyright and Disclaimer Notices
HILDA Disclaimer
This paper uses unit record data from the Household, Income and Labour Dynamics in Australia (HILDA) Survey. The unit record data from the HILDA Survey was obtained from the Australian Data Archive, which is hosted by The Australian National University. The HILDA Survey was initiated and is funded by the Australian Government Department of Social Services (DSS) and is managed by the Melbourne Institute of Applied Economic and Social Research (Melbourne Institute). The findings and views based on the data, however, are those of the authors and should not be attributed to the Australian Government, DSS, the Melbourne Institute, the Australian Data Archive or The Australian National University and none of those entities bear any responsibility for the analysis or interpretation of the unit record data from the HILDA Survey provided by the authors.
CoreLogic Disclaimer
The following Disclaimer Notice applies to content that uses data from CoreLogic:
This publication contains data, analytics, statistics, results and other information licensed to us by RP Data Pty Ltd trading as CoreLogic Asia Pacific (CoreLogic Data)
© Copyright 2020. RP Data Pty Ltd trading as CoreLogic Asia Pacific (CoreLogic) and its licensors are the sole and exclusive owners of all rights, title and interest (including intellectual property rights) subsisting in the CoreLogic Data reproduced in this publication. All rights reserved.
The CoreLogic Data provided in this publication is of a general nature and should not be construed as specific advice or relied upon in lieu of appropriate professional advice.
While CoreLogic uses commercially reasonable efforts to ensure the CoreLogic Data is current, CoreLogic does not warrant the accuracy, currency or completeness of the CoreLogic Data and to the full extent permitted by law excludes all loss or damage howsoever arising (including through negligence) in connection with the CoreLogic Data.
Acknowledgements
The Discussion Paper series is intended to make the results of the current economic research within the Reserve Bank available to other economists. Its aim is to present preliminary results of research so as to encourage discussion and comment. Views expressed in this paper are those of the authors and not necessarily those of the Reserve Bank. Use of any results from this paper should clearly attribute the work to the authors and not to the Reserve Bank of Australia.
Footnotes
Otto (2007) examines the effect of changes in mortgage interest rates on housing prices across Australian capital cities. However, he does not examine the heterogeneity in responses within cities nor link it to monetary policy. [1]
The only Australian study of which we are aware is Lim and Tsiaplias (2018). They find that the stance of monetary policy has varying (nonlinear) effects across city-based housing markets in Australia. We extend their analysis by allowing the sensitivity of housing prices to interest rates to vary for each individual local housing market. We also more closely examine which economic variables matter to this sensitivity. [2]
Cooper et al (2016) is the study most similar to this paper, although they ask a slightly different research question. We are interested in the effect of an aggregate shock (national monetary policy changes) on regional housing prices. They study the effect of regional monetary shocks on regional housing prices, with their identification strategy implicitly abstracting from the aggregate effects of national monetary policy changes. The regional monetary policy shocks are estimated based on a counterfactual monetary policy rule for each US state. [3]
Del Negro and Otrok estimate a dynamic factor model on US state data and find that most of the variation in local housing prices is explained by regional shocks, with a limited role for monetary policy. However, their sample period excludes the national housing price cycle over the mid to late 2000s, which some have linked to the stance of monetary policy. For a summary of the debate on this, see Dokko et al (2011). [4]
Beraja et al (2019) indicates that the regional distribution of housing equity influences the aggregate effect of monetary policy, and that lower levels of equity are associated with regions being less responsive to interest rate cuts due to a reduced ability to refinance mortgages. [5]
For an overview of research on the links between monetary policy and inequality, see Colciago, Samarina and de Haan (2019). [6]
We could instead derive empirical predictions from a user cost of capital model, as used, for example, by Fox and Tulip 2014 (and references therein). This is basically the same framework, with a focus on housing price growth (rather than rental yields) and without the added complexity of introducing depreciation and taxes on housing in deriving the required rate of return. [7]
This implicitly assumes that the housing price-to-rent ratio is approximately constant over time, which is a reasonable assumption over the sample period from 1990 to 2019. [8]
The weight is equal to where is the sample average of the log ratio of rents to housing prices. [9]
The specification assumes that the correlation between changes in housing prices and current rents does not vary by local housing market, which is essentially the same as assuming a stationary price-to-rent ratio. [10]
We also have estimates of current rents by SA3 and quarter so that current rental growth can be included as an explanatory variable in the model. However, the available time series of these data only cover the period since 2005. So these data are mainly used for robustness. [11]
This provides some tentative evidence that the effects of monetary policy on housing price growth are not coming through current rents but instead through its effect on housing price expectations and discount rates. But the lack of data, and hence degrees of freedom, reduces the precision of the estimates. [12]
These estimates are smaller than estimates for other recent Australian studies. For example, Saunders and Tulip (2019) and the RBA's MARTIN model estimate a peak effect of around 9 per cent and 4 per cent respectively, following a temporary 100 basis point change in the cash rate. However, the Saunders and Tulip estimates are based off a temporary three-year increase in the cash rate. [13]
In the model, the coefficient would be positive and relatively large, which implies a larger negative effect of monetary policy on housing prices. [14]
The sample is smaller than the population of SA3 regions due to missing data. [15]
More information on these methods can be found in Hastie, Tibshirani and Friedman (2009). [16]
The ABS regional data are typically drawn from the Census or Australian Taxation Office (ATO) data. The full list of variables can be found in Appendix A. [17]
To fully account for the dynamics of housing price responses to monetary policy it is important to consider different time horizons. It is possible that a variable may be important at one horizon but not at others. Though model selection methods could be used we do not think that would produce interpretable results across multiple horizons. For more consistent and interpretable results across time horizons we take signal from our model selection results while applying judgement and focusing on OLS estimates. [18]
Elastic net is less discriminate than LAR. This is because elastic net is designed to allow for ‘groupings’, which allows for multiple highly correlated variables to be selected by averaging their effects, as opposed to choosing one over the rest. [19]
It is also consistent with US research that suggests that financing constraints have a limited effect on housing prices because constrained individuals comprise a small share of the housing market. Instead, it is the unconstrained individuals that drive housing prices (Kiyotaki, Michaelides and Nikolov 2011). [20]
It is worth noting that there are many variables that were tested and proved to not be correlated with the local housing price sensitivity. These variables include those that have been identified in past research as being potentially important, such as the age structure of the population (Wong 2019) and the industry composition of each region (Vespignani 2013). [21]
The analysis uses a hedonic index to measure housing prices so as to abstract from differences in the quality of housing. But part of the heterogeneity in the response of local housing markets may be through changes in housing quality, leading us to underestimate the differential effects of monetary policy. We also estimate the restricted model using median sales prices as the dependent variable. The baseline results are robust to this change. The expensive areas respond by more, and the heterogeneity in price responses across regions is very similar. This suggests that the quality of the housing stock does not change much in response to monetary policy over a two-year horizon. [22]
Estimates when using the price groups defined in our baseline restricted model produce a similar finding that there is no strong evidence for land availability driving the heterogeneous response of housing prices across the distribution of housing wealth. [23]
More details in Appendix B. [24]
We also tested whether supply constraints were driving the price responses by examining how dwelling investment responds to monetary policy changes across local housing markets. However, our proxy for dwelling investment – home building approvals – was too noisy at a quarterly frequency (and over a relatively short time window) to generate any meaningful results. [25]
It is possible to calculate the absolute effects of monetary policy on housing prices across regions using these shocks. However, an ideal measure of monetary policy shocks would purge changes in the cash rate only from anticipated changes in housing prices. This measure purges more than just the anticipated changes. [26]