RDP 2019-10: Emergency Liquidity Injections 2. The Model
October 2019
- Download the Paper 2,094KB
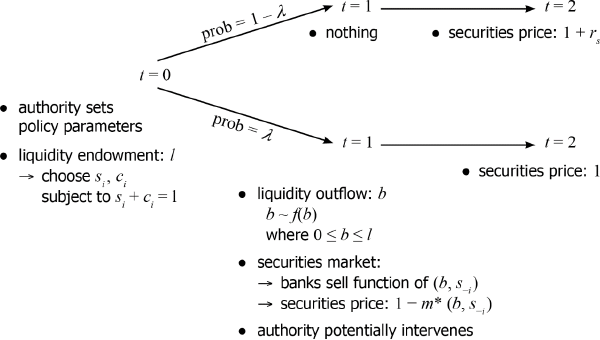
The model has three dates, t = 0, 1, 2, and three types of agents: the authority, a continuum of risk-neutral banks, and securities buyers. The modelling goal is to compare policies by how well the authority can achieve its objectives given banks' reactions to the policy and their interactions with securities buyers. The time line is:
- The authority announces its policy parameters, such as the interest rate on emergency lending, given the type of liquidity injection policy. Banks then choose their asset-side liquidity risk to maximise their expected date 2 pay-off .
- A liquidity shock may occur, whereby banks experience a randomly drawn outflow of cash. Banks can cover a cash shortage by selling securities to securities buyers or by obtaining emergency funds from the authority. The market price for securities equilibrates banks' demand for liquidity via sales with securities buyers' optimal liquidity supply.
- If there was a liquidity shock at date 1, market liquidity and the securities price recover. If there was no liquidity shock, securities pay positive returns.[4]
2.1 Banks and the Liquidity Shock
At date 0 the continuum of risk-neutral banks each have a liquid endowment l. They can allocate l between two types of liquid assets – securities ‘s’ and cash ‘c’. Securities have positive expected returns, but if there is a liquidity shock, market illiquidity can depress their prices. Cash has zero net return but always holds its value. Denote bank i's securities choice by si. The date 0 securities price is normalised to 1 so ci + si = 1 for all i.
Denote the set of choices (i.e. the strategy profile) of a unit measure of banks that excludes bank i as s–i, and the set of all banks' choices as s. This can be thought of as the mapping s : [0, 1] → [0, l], which is assumed non-decreasing and integrable in i. Total securities held by banks is defined as . The statement s–i = S indicates that a unit measure of banks each hold S – i.e. a (virtually) symmetric choice across other banks – and indicates there is a positive measure of banks not choosing S. The statement s = S indicates fully symmetric choices at S.
At date 1, with probability , where , nothing happens and at date 2 securities are worth 1 + rs > 1. With probability there is a liquidity shock and every bank must provide cash b, drawn randomly from distribution f (b) which is positive and continuous on [0, l). The shock b can be interpreted as short-term creditors not rolling over debt, withdrawing depositors, credit line drawdowns, or unexpected margin requirements.
2.1.1 Discussion
The investment decision resembles the classic portfolio decision in Diamond and Dybvig (1983). Cash ci represents cash and highly liquid low-return securities such as government bonds, whereas securities can be thought of as relatively safe privately issued debt. Banks' other non-marketable assets are treated as outside this liquidity management decision. The simplifying dichotomy resembles how liquidity risk management is interpreted by the liquidity coverage ratio (LCR) of Basel III, which requires banks to hold a sufficient quantity of high-quality assets with low market liquidity risk, distinguishing them from lower quality securities.[5] It is also motivated by the fact that banks had high exposures to assets with markets that were liquid before the crisis, but became illiquid during the crisis, as documented with respect to private secured lending markets by Hordähl and King (2008) and Gorton and Metrick (2012), and with respect to asset-backed securities markets by, for example, Brunnermeier (2009).
2.2 Securities Buyers and the Date 1 Securities Market
Given a liquidity shock at date 1, if ci < b then bank i must satisfy its cash shortage by selling securities or borrowing from the authority. Banks can sell securities to securities buyers or other banks with spare cash (although the paper focuses on symmetric bank choices). For now, assume that bank i only borrows from the authority any shortage it cannot meet with its cash and securities. This assumption permits the authority's behaviour to be described separately; it is relaxed in Section 2.4.
Securities buyers maximise profit by allocating their limited cash across securities purchases and an outside investment option. The outside investment has continuously decreasing net returns that are bounded and equal zero when all their cash is invested. Securities buyers are assumed capable of short selling, which prevents prices rising above 1, and have at least l cash, so can buy all securities held by banks if the returns are high enough. Given date 1 securities price 1 − m, securities buyers' optimal expenditure on securities (LS) therefore satisfies:
where and is positive and continuous. The market-clearing securities price is written 1 – m* where m* represents market illiquidity. The characteristics of securities buyers imply for any demand schedule.
Banks' total demand for liquidity from the securities market, in cash value, is written LD. Denote the quantity of securities sold by bank i as sim, and the total quantity of securities sold by banks as Sm, implying that . For example, if b > ci for all i and no bank needs to borrow from the authority, then sim (1 – m) = b – ci and
Date 1 securities market equilibrium requires that m* satisfies
where b is exogenous, and other variables in LD are determined at date 0.
Figure 1 illustrates m* for two different forms of LD (which correspond to the functional form in Equation (5) later in this section). When banks have spare cash, so , market illiquidity m* is zero, illustrated by and . If LD(m) > 0 then securities buyers buy securities from banks, and m* is where the price is low enough that securities buyers are willing to divert sufficient funds from their outside option to meet the liquidity demand. This is illustrated by and .
Market illiquidity m* is an implicit function and in some cases can be more intuitively expressed as the inverse of the Ls function. This is denoted M such that . The characteristics of LS imply that M (LD) = 0 for all , and that the first derivative of M, written M′, is continuous and positive for all LD > 0. The general expression for equilibrium market illiquidity used throughout this paper, given policy P, is , acknowledging that banks' date 1 securities selling Sm is determined by b and their date 0 securities choices s–i. Sometimes the P subscript will be dropped if the policy type is obvious or irrelevant.
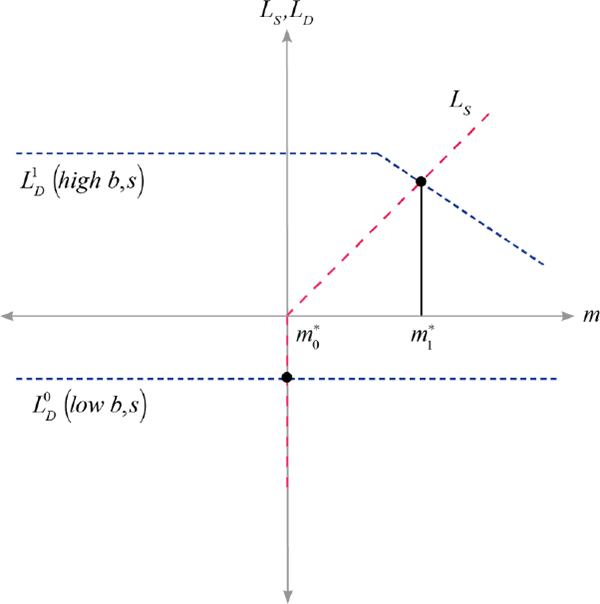
Notes: Illustrates equilibrium securities market illiquidity m*, corresponding to equilibrium price 1 – m*, as the intersection between supply of liquidity from securities buyers and demand for liquidity by banks. LS is a representation of Equation (1). The two schedules of LD are consistent with Equation (5), with representing higher b and/or s than . The kink in reflects the point at which banks are selling all their securities. The axis lines are at zero.
The date 1 value of bank i's liquid assets – its cash and securities prior to any borrowing from the authority – is ci + si (1 – m*) = l – sim*. Therefore, when it does not borrow from the authority, its date 1 liquidity position is l – sim* –b. The liquidity shock that would expend precisely all of bank i's liquid assets is written . Specifically, the implicit function is defined by
If then bank i can meet its cash shortage by selling securities. Banks are assumed to buy at date 1 if they have spare cash and are indifferent between buying and selling. If then bank i is liquidity deficient and must obtain funds from the authority. Given the temporary assumption that banks minimise borrowing from the authority, if s = S (i.e. symmetry) then market illiquidity takes the form
2.2.1 Discussion
Securities market illiquidity is the key market imperfection in the model, caused by bounds on private entities' supply of cash. Banks would never become distressed if securities could always be liquidated at net present value. The market clearing mechanism is similar to Diamond and Rajan (2011) and Stein (2012). It is a generalisation of the cash-in-the-market pricing of Allen and Gale (1994), such that the cash available for securities purchases continuously increases as the market price falls. Ample liquidity returns to the market at a later date, bringing the securities price back to its net present value. Liquidity-driven selling can therefore push prices below their (discounted) future value, consistent with empirical studies of securities prices such as Coval and Stafford (2007), Hameed, Kang and Viswanathan (2010), Longstaff (2010) and Merrill et al (2014).
Funding liquidity and market liquidity are linked by the constraint that if a bank's outflow of short-term liabilities cannot be funded by cash, it must be met by liquidating assets. This link is why the LCR requires banks to hold a quantity of HQLA that depends on their short-term liabilities. It is empirically documented by Nyborg and Östberg (2014), who term such securities liquidation as ‘liquidity pullback’, and by Fontaine and Garcia (2012). This model feature resembles the ‘liquidity spiral’ in Brunnermeier and Pedersen (2009), whereby to meet a tightened capital constraint, investors must sell assets, pushing down the asset price and further reducing the value of their capital.
2.3 An Example of m* and
Consider the market illiquidity function
where . Assume that s = S and market illiquidity is consistent with Equation (5). Symmetry implies that is the same for all banks; denote this . Market illiquidity satisfies
From Equation (4), the threshold can be solved as
Figure 2 plots the market illiquidity function (Equation (6)) for two fixed values of S such that 0 <S′ < S″ < l. Given S, for b below the first kink (on the x axis), at b = l – S, banks' net securities sales are zero and there is no market illiquidity, as is the case for in Figure 1. Above the second kink at , banks are liquidity deficient and selling all their securities to securities buyers, so m* is flat. When S increases, market illiquidity rises at all b > l – S and both kinks shift left.
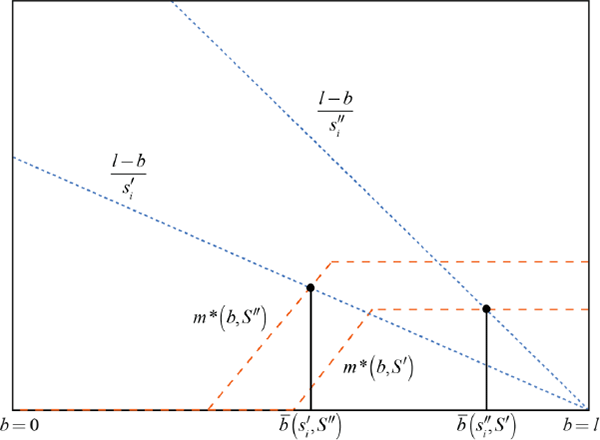
Notes: Represents as the intersection between: (i) market illiquidity m*, which is increasing in b as described in Section 2.2; and (ii) the bank's ability to handle market illiquidity, which is decreasing in b because the higher the liquidity shock, the more liquidity the bank needs to obtain through securities sales. Market illiquidity m* is as characterised in Equation (5) with and . Securities holdings satisfy
Also shown is bank i's capacity to survive market illiquidity (l – b)/si for two fixed values of si such that . The intersection of m* and (l – b)/si determines because bank i avoids liquidity deficiency if and only if . For any si > 0, at b = l bank i cannot survive any market illiquidity because the liquidity withdrawal requires its full date 0 liquid endowment. An increase in si pivots bank i's illiquidity capacity anticlockwise around (l, 0), lowering its and reducing its probability of avoiding liquidity deficiency for any given S.
2.4 The Authority and Equilibrium
The model outcomes are compared across different types of liquidity injection policies P. The authority has full information and, given policy P, announces the policy parameters p (such as the interest rate) at the start of date 0. At date 1, the authority provides liquidity on the terms announced. Banks always accept a liquidity injection rather than failing.[6] Figure 3 summarises the time line of events.
The authority sets the policy parameters to maximise its objective W, defined on: whether there are any bank failures banks' liquidity risk (S), which maps directly to the probability of an intervention being required; and banks' expected profits , which represents ex post banking system health. Preventing bank failures is prioritised above all else, but given this, no particular weighting is assumed on the other two objectives. Specifically, the authority maximises the objective function
where w1 is a positive constant such that w1 > maxp{w2}, and w2 satisfies and
The authority is assumed to prioritise the objectives embedded in W over any effects on its own balance sheet. This objective function represents the view that, during a severe crisis, profits and balance sheet exposure are less of a concern to the authority than the health of the financial system. Consistent with this view, the crisis in this model involves excess demand for liquidity, so for a liquidity-rich authority, interventions tend to have low risk relative to returns. Indeed, authorities made profits on several of the crisis interventions in 2008 and 2009. Swiss National Bank (2013) writes about its liquidity provisions to UBS: ‘attaining a profit was never an objective in its own right. The prime reason for the establishment of the StabFund was its contribution to strengthening the Swiss financial system’.
The preferences represented by W are assumed time consistent. Otherwise, the authority could announce penalty rates in an attempt to induce low liquidity risk, then at date 1 charge lower rates than it announced, to raise banks' post-crisis profits. Time consistency of this objective function is appropriate for two reasons. First, the too-big-to-fail problem is built directly into the authority's first priority – policies under which banks fail are time inconsistent. Second, penalty rates have the ex post benefit to the authority of deterring excessive use of its balance sheet, which is the justification for penalty rates put forward by Bagehot (1920).
The paper focuses on the following three policies (P, p):
- Unsecured lending (u, ru): the authority lends any quantity of emergency funds to bank i, with repayment at date 2 of ei (1 + ru), where ru > 0.
- Secured lending (also called repo) (R,(rR,h)): the authority lends any quantity of funds to bank i, provided that bank i provides the authority ei/(1 – h) securities as collateral (where h is the haircut), with repayment at date 2 of ei (1 + rR), where rR > 0.
- Securities purchase (S,mS (b)): the authority determines an acceptable schedule of market illiquidity mS (b) and purchases sufficient securities such that the date 1 market price does not fall below 1 – mS(b).
Denote by the pay-off maximising securities holdings for bank i given the choices of other banks and the policy. That is,
An equilibrium (p) is a choice set satisfying for all i, with corresponding aggregate securities holdings written . An optimal equilibrium is an equilibrium in which policy parameters p are set to maximise W; specifically,
The P subscripts will sometimes be dropped when there is no ambiguity.
Footnotes
It is a simplifying assumption that, given a liquidity shock, the date 2 securities price is 1 rather than 1 + rs. This could easily be relaxed but would complicate the notation. [4]
[t]he objective of the LCR is to promote the short-term resilience of the liquidity risk profile of banks. It does this by ensuring that banks have an adequate stock of unencumbered high-quality liquid assets (HQLA) that can be converted easily and immediately in private markets into cash … (Basel Committee for Banking Supervision 2013, paragraph 1)The approach also matches Saunders and Cornett (2008)'s textbook definition of liability-side liquidity risk management:
When liability holders demand cash by withdrawing deposits, the [financial institution] FI needs to borrow additional funds or sell assets to meet the withdrawal. The most liquid asset is cash; FIs use this asset to pay claim holders who seek to withdraw funds. However, FIs tend to minimize their holdings of cash reserves as assets because those reserves pay no interest. To generate interest revenues, most FIs invest in less liquid and/or longer-maturity assets. While most assets can be turned into cash eventually, for some assets this can be done only at a high cost when the asset must be liquidated immediately. The price the asset holder must accept for immediate sale may be far less than it would receive with a longer horizon over which to negotiate a sale. (pp 493–494)[5]
A sufficiently high cost of failure would induce the same results. For example, banks could be assumed to hold non-marketable assets with very high liquidation or transfer-of-ownership costs. [6]