RDP 2019-10: Emergency Liquidity Injections 4. Liquidity Injection through Secured Lending
October 2019
- Download the Paper 2,094KB
Under a secured lending policy, when a bank borrows from the authority it must provide securities as collateral, which introduces a constraint on its securities sales. The policy can be interpreted as raising the amount of liquidity that a bank can extract from its securities holdings. A security's ‘liquidity value’ if sold is the illiquid price 1 – m*, and if used as collateral is 1 – h where h is the haircut set by the authority. If banks would fail without an intervention, then h < m* is a necessary condition for the policy to avert bank failures. For tractability the following assumes that the authority sets h = 0, which is the lowest non-negative haircut that eliminates its counterparty risk, and which also permits the simplification that h does not depend on b (from the requirement that h < m*). The assumption that h = 0 implies securities retain their full liquidity value if used as collateral, which is discussed later in this section.
The secured lending policy is characterised by Equation (9) (after replacing ru with rR) and Equation (10), but the feasibility constraint Equation (11) is replaced by the collateral constraint:[10]
The collateral constraint does not bind if: (i) bank i has spare liquidity or (ii) borrowing from the authority is not more costly than selling securities , in which case bank i can maximise its pay-off with sim = 0. In these cases the securities market outcomes resemble the unsecured lending policy. As under the unsecured lending policy, if rR < rpen then there is some b at which the interest rate places an upper bound on market illiquidity at rR/(1 + rR). Alternatively, if rR > rpen then condition (ii) never holds.
Lemma 3. For given symmetric s > 0, if rR ≤ ru then expected market illiquidity m* (across b) is strictly lower under the secured lending policy than under the unsecured lending policy, because there is necessarily some b at which the collateral constraint Equation (17) binds.
Figure 4 illustrates Lemma 3. A bank's collateral constraint binds whenever its collateral obligations force it to divert securities away from another use. Collateral constraints necessarily bind for high enough liquidity shocks, when banks have large borrowing requirements and most of their securities are being provided as collateral. If rR is sufficiently high, collateral constraints also bind for smaller shocks, when banks' borrowing needs are low but they would still prefer to sell all their securities and borrow less. Either way, binding collateral constraints mean fewer securities are sold, and market illiquidity is lower, than would be the case without collateral constraints.[11]
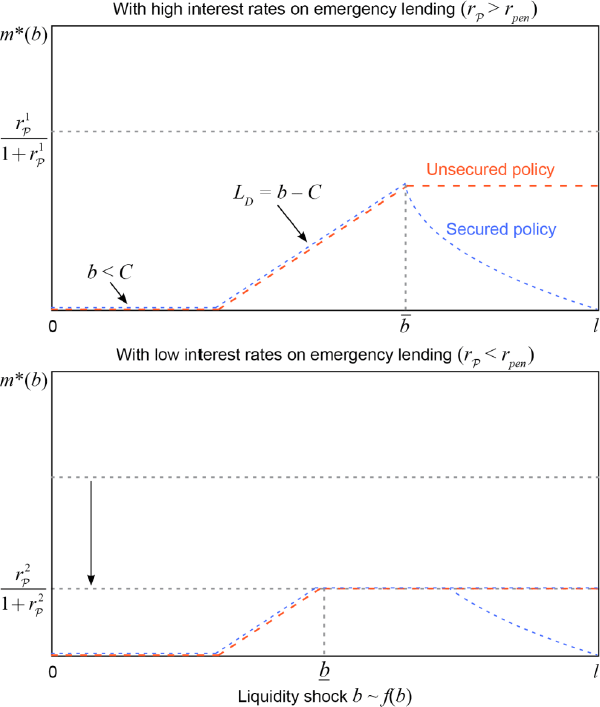
Notes: The two panels illustrate market-clearing market illiquidity m* across b, holding s constant, for two different interest rates , but equal interest rates across the two policies. In the lower panel, , imposes a bound on market illiquidity.
When Equation (17) binds, Equations (10) and (17) hold with equality, implying that bank i's borrowing is
and securities sales are
A binding collateral constraint means that the quantity of securities sold (l – b)/m* does not depend on securities held si, because liquidity deficiency implies that any increase in si (and corresponding reduction in ci) raises bank i's borrowing needs one for one. Therefore, any additional securities held are simply used as collateral. If h were assumed positive, sim would be negatively related to si, because an increase in si would raise borrowing needs by more than the additional securities could collateralise.
Therefore, if , bank i's ex post pay-off (from Equation (9)) is
The return on liquidity rR /m* is the interest cost on necessary borrowing, because collateralising one unit of borrowing means losing 1 – m* liquidity through foregone sales, so to obtain one more unit of liquidity, borrowing must increase by 1/m*. This imposes (1 + rR)/m* repayment cost and saves 1/m* on securities used as collateral rather than sold. Observe that m* = rR /(1 + rR) implies 1/ (1 – m*) = rR / m*, so the ex post pay-off satisfies Equation (20) whenever .
Bank i's pay-off is therefore
Proposition 4. Assuming symmetric choices s, there is a unique equilibrium . If rs is low enough relative to rR is strictly decreasing in rR, bound below only at zero. If the optimal unsecured policy equilibrium is interior, the optimal secured policy equilibrium has higher W.
Market illiquidity negatively affects bank profits, evident in Equation (21). However, it does not negatively affect the marginal return to securities and incentivise liquidity risk-taking, for two reasons. First, banks individually have no impact on the securities price, so a weakening of the collective impact does not factor into their decision-making. Second, banks with more liquidity risk are just as constrained from participating in the securities market than banks with fewer securities, because they need to collateralise more borrowing. This means that the avoided losses from improved market liquidity are not positively related to ex ante securities holdings. The overall result is that the collateral constraint improves market liquidity, offsetting fire sale externalities, and reducing banks' losses without incentivising greater liquidity risk-taking.
The model demonstrates several other features of a secured lending policy. As mentioned earlier in this section, the authority's haircuts need to be set to ensure banks can get more liquidity from their securities than the private market offers them, or otherwise the policy has little capacity to save banks. Allen and Carletti (2008) make a similar recommendation, arguing that collateral should be valued based on what the price would be in a liquid market, using models and inputs such as prices in other markets that are active. They relate this to the Bagehot (1920) recommendation that ‘advances should be made on all good banking securities’ (p 188) and explain that it is permitted by accounting standards. This principle was arguably followed in 2008 and 2009, when many central banks substantially widened the range of repo-eligible collateral, after private markets for those securities dried up. Cecchetti (2009) writes about the Fed's emergency lending:
The rules of the Term Auction Facility allow banks to pledge collateral that might otherwise have little market value. Under the rules of the auctions, TAF loans must be over-collateralized by at least a factor of two, but in reality the Fed is taking collateral at a price that is almost surely above its actual market price (p 67).
A related implication of this collateral valuation principle is that central banks' haircuts during liquidity crises should not be calibrated only on securities price volatility, which is typical practice during normal times and for haircuts in private markets. If securities price movements reflect market illiquidity, they do not necessarily imply riskier collateral for the central bank, which is not susceptible to liquidity shortages. More importantly, the principle demonstrates that unnecessarily high haircuts can lead to illiquidity-driven bank failures, having the perverse effect of increasing the central bank's counterparty risk rather than decreasing it.
Another policy feature illustrated by the model is that the collateral constraint, when binding, forces banks to borrow more than they would without a constraint, because every unit of borrowing means 1 – m* less liquidity that can be drawn from the securities market. Relative to an unsecured lending policy, this amplifies the penalising effect of a given level of penalty rates, by increasing the borrowing that takes place at those rates. Corollary 5 states this result.[12] Holding liquidity risk-taking constant, this also implies more expansion of the authority's balance sheet for a given shock. A cost of the balance sheet expansion is that a bank's other creditors lose any claim on securities the bank provides the authority as collateral, if the bank were to default at date 2. However, this section has shown that the authority's trade-off between liquidity risk and banking system profits is weaker under the secured policy, so the authority may opt for greater penalties and therefore less borrowing, relative to an unsecured lending policy. Further, the authority arguably takes on less balance sheet risk under the secured lending policy, because its lending is collateralised.
Corollary 5. If rR = ru > rpen then whenever S* < l.
Footnotes
If h were positive, ei in Equation (17) would be replaced by ei /(1 − h). [10]
The same reasoning implies that the degree of market illiquidity would tend to be decreasing in h. [11]
Higher haircuts would increase the degree of amplification, by requiring banks to divert more securities from selling for a given quantity of borrowing. [12]