RDP 2019-09: Australian Money Market Divergence: Arbitrage Opportunity or Illusion? 4. Sensitivity Analysis
September 2019
- Download the Paper 1,465KB
In this section we test the sensitivity of the outputs to the key assumptions of the model in order to test the robustness of our findings.
4.1 Debt Funding Rate
The decline in net returns from money market investments, attributable to the narrowing in the spread between gross returns and the average debt funding rate, is a key result of our methodology.
In the baseline derived above, we defined the debt funding rate as the average of all debt (non-equity) sources. This assumes that all investment activity is funded at the aggregated balance sheet level. We believe this reflects how the major banks broadly manage their balance sheet composition and compliance with prudential standards. For example, equity is raised based on the aggregate balance sheet requirement. However, this is not an entirely accurate description of how banks operate their individual business lines on a day-to-day basis. Money market desks typically either source marginal funding externally or are charged an overlay fee for funding sourced internally (i.e. transfer price).[11] Therefore, the debt funding rate faced by the relevant money market desk might differ from the rate we derive in preceding sections.
To test the sensitivity of net returns from money market investments to a different mix of funding rates, we consider two scenarios and compare them to the baseline results derived above. Both relax the assumption that the average debt funding rate is the relevant input into the calculation of net returns. Instead, debt funding for these money market investments is externally sourced in a market where interest rates are relatively low. The share of equity funding these investments remains unchanged from the baseline.
In the first instance, we make the deliberately extreme assumption that investments can be funded at the overnight cash rate target. In recent years this assumption improves net returns relative to the baseline (Figure 8). Between 2016 and 2018, borrowing at the cash rate and lending into the repo market, the bank bill market, or foreign exchange swaps (JPY or USD), improved on baseline net returns by around 20 basis points. Notably, even when funded at the cash rate, foreign exchange swaps directed into USD were not profitable for the supervised major banks until forward rates began to rise substantially in 2018. However, these results are upwardly biased because funding at the cash rate implies lower costs than any of the accessible money market alternatives.
In the second scenario, we test the sensitivity of the baseline results to a switch in funding to the repo market. Borrowing under repo to lend into the repo market is a zero-sum game. Net returns from borrowing under repo to lend cash into the bank bill market remained negative in 2018. The relative riskiness of the trade implies the use of more equity funding and in the second half of 2018 the repo rate was higher than the bank bill rate. The implication is that there has been insufficient economic incentive to arbitrage between the two markets. Similarly, borrowing in the repo market to lend cash under swap in USD does not appear to have been a profitable investment for the major banks since around the beginning of the sample. For repo funding to yield a positive net return from money market investment requires surprisingly wide spreads such as those observed in the JPY foreign exchange swap market. The net return for major banks borrowing under repo to lend into the JPY swap market peaked at around 50 basis points before narrowing to around 15 basis points for most of 2017–18 and becoming negative since late 2018. This finding also further substantiates the link between the repo rate and foreign exchange swap rates described in Becker and Rickards (2017), whereby non-resident investors borrow in the repo market in order to take advantage of the basis trade.
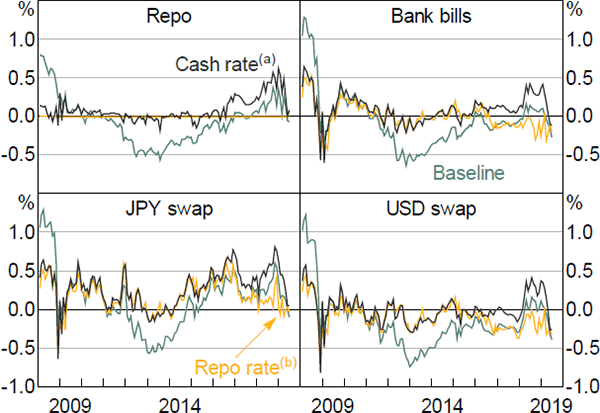
Notes:
(a) Assumes that debt is funded at the cash rate
(b) Assumes that debt is funded at the repo rate
Sources: APRA; Authors' calculations; Bloomberg; RBA
Our approach does not measure the degree to which arbitrage is already reflected in observed money market rates. That is, it could be possible that arbitrage activity has led to a convergence between funding and investment rates so as to exhaust profitable trading opportunities. Some of the changing dynamics in money markets in 2018, where repo, bank bill and foreign exchange swap rates have become more volatile and correlated, may in part be explained by the return to slightly more favourable net returns as described in this paper. However, the methodology is a useful framework to explain why there is not complete convergence between market rates.
4.2 Equity Funding Rate
To test the sensitivity of our results to the equity funding rate we also derive an additional estimate from a specification of the CAPM approach. We assume investors adaptively base their expectations of market risk premia on trends observable in the recent past. Specifically, we calculate the market risk premium at time t as the difference between the average annual return on the All Ordinaries Index of equities over the past 15 years and the yield on 10-year Australian Government securities. This calibration is very sensitive to past market movements (and in particular, the sharp price falls that occurred during the financial crisis) and may be a downward-biased estimate of the equity funding rate. Nonetheless, our results remain largely unchanged from the baseline under this approach (Figure 9).
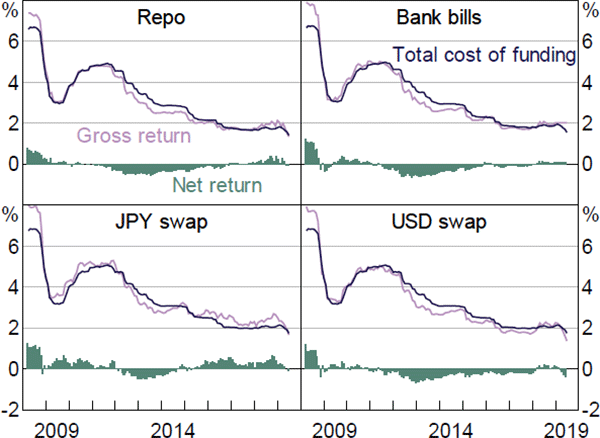
Sources: APRA; Authors' calculations; Bloomberg; RBA
4.3 Risk Weights
The amount of equity required to fund a money market investment is determined by its risk weight. The risk weight is calibrated according to the likelihood and magnitude of potential losses on an investment. Intuitively, trades that are less risky attract lower risk weights. In our analysis, risk weights are driven by two key factors (Table 1). First, the creditworthiness of the borrower is a proxy for their ability to repay the loan at maturity. Lending cash to a borrower with a higher credit rating increases the likelihood of full repayment at maturity and is associated with a lower risk weight. Second, loan collateralisation reduces the risk exposure to the borrower. If the borrower defaults, the cash lender may recoup most (or all) of their investment by selling the collateral. As such, less of their investment is ‘at risk’ and this is associated with a lower risk weight.
| Transaction and borrower characteristics | Probability of default | Loss given default | Likelihood of losses | Size of risk weight |
|---|---|---|---|---|
| Uncollateralised transaction (e.g. bank bills) |
||||
| AA-rated borrower | Lower | High | Lower probability of high losses | Small |
| BBB-rated borrower | Higher | High | Higher probability of high losses | Large |
| Collateralised transaction (e.g. repo) |
||||
| AA-rated borrower | Lower | Low | Lower probability of low losses | Very small |
| BBB-rated borrower | Higher | Low | Higher probability of low losses | Very small |
|
Sources: APRA; Authors' calculations |
||||
Consider two stylised examples to demonstrate how the creditworthiness of the cash borrower and the collateralisation affect the risk weight on an investment. In both examples Bank A is seeking to invest cash for three months.
Bank A can lend the cash on an uncollateralised basis by buying a bank bill issued by Bank B. Bank A is exposed to default on the whole face value of the bank bill. The likelihood of this occurring varies with the creditworthiness of Bank B (the borrower). Therefore, the risk weight on unsecured transactions can vary from low (if the borrower is highly rated) to high (if the borrower has a low credit rating), reflecting the expected loss on the investment. Risk weights on uncollateralised trades vary significantly depending on the creditworthiness of the borrower.
Alternatively, Bank A can collateralise its investment by lending to Bank B under repo. Collateralisation significantly reduces the likelihood – and magnitude – of potential losses. If Bank B defaults, Bank A can sell the collateral to recoup their investment. As a result, risk weights on collateralised trades tend to be lower.
Due to the large variation in possible risk weights, we evaluate the sensitivity of our results to changes in risk weights (Figure 10). We use baseline assumptions for risk weightings where domestic investments are AA-rated (in line with the major banks in Australia), and foreign investments are A-rated to reflect lower credit worthiness (e.g. Japanese banks).
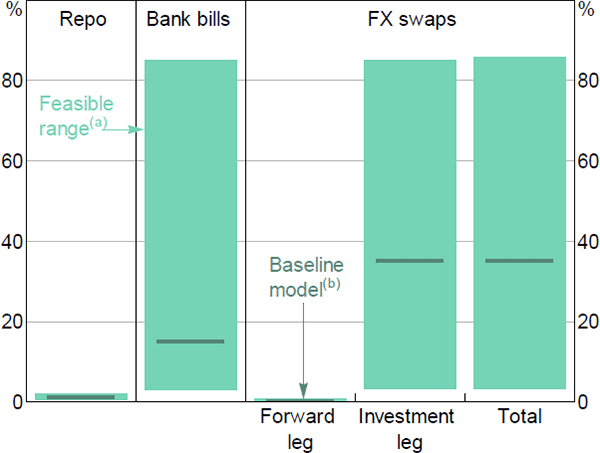
Notes:
(a) Based on counterparty credit rating, from AA (lowest risk weight) to BBB (highest risk weight) and
possible treatment under Trading Book and Banking Book
(b) Based on AA rating for repo and bank bills; and A rating for foreign exchange swaps
Sources: APRA; Authors' calculations; RBA
Figure 11 depicts the possible dispersion in net returns when allowing risk weights to vary. For repo transactions, the range of possible risk weights is narrow since collateralisation reduces the risk exposure of the investor. As a result, net returns do not vary widely with a change in borrower credit rating. In contrast, where the investment is uncollateralised (such as bank bills), the range of possible net returns becomes much wider. For investments involving bank bills (domestic or foreign under swap) we find the net return becomes more negative as borrower creditworthiness deteriorates and the risk weight increases. As the creditworthiness of the borrower improves for swaps into USD, net returns improve but typically remain negative. Over recent years, the baseline net return on JPY swaps would have remained positive even if risk weightings had increased significantly.
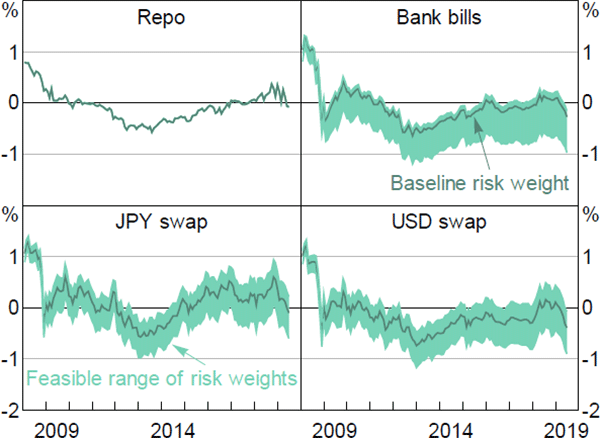
Note: See notes to Figure 10
Sources: APRA; Authors' calculations; Bloomberg; RBA
4.4 Leverage Ratio Considerations
The leverage ratio constrains the amount of debt financing that banks can take on by setting the minimum equity to be held against total assets. Consequently, it also limits the scope banks have to lower their funding costs by substituting relatively cheap debt for equity. Prudential standards require banks to fund total assets with at least 3 per cent of ‘Tier 1’ equity capital.[12] Currently, the leverage ratios of major banks in Australia are significantly above this regulatory minimum so as not to be a binding constraint.
However, the leverage ratio could constrain arbitrage at the margin by limiting the ability of banks to take on the significant amounts of additional leverage that might be required to close the spreads observable to date. There might also be a reluctance, even at the conservative leverage positions, for any one bank to take on significantly more debt than its peers.
Footnotes
In order to disincentivise the use of internal funding for trading activities, treasuries may set the debt funding cost applicable to money market trades higher than the average debt funding rate (Wakeling and Wilson 2010). [11]
APRA (2018) announced plans to increase this requirement to 3.5 per cent for banks using the internal ratings-based approach. [12]