RDP 2019-09: Australian Money Market Divergence: Arbitrage Opportunity or Illusion? 2. Estimating Funding Costs, Gross Returns and Net Returns
September 2019
- Download the Paper 1,465KB
The net return (NRit) a bank earns on a position in an asset i at time t is calculated as the gross return (GRit) on the asset less the total cost of funding the position (TCit):
This methodology explicitly accounts for differences in asset-specific funding costs, which is important because prudential standards generally require banks to fund riskier assets with a higher share of equity capital (which is more expensive than debt).[3] Equation (1) can be rewritten to specifically account for the shares of total funding attributable to equity and debt :
The total cost of equity is calculated as * EFRt where EFRt is the equity funding rate (i.e. the price of equity funding) and is the portion of asset i funded by equity (i.e. the quantity of equity). Similarly, can be expressed as * DFRt where DFRt is the debt funding rate (i.e. the price of debt funding) and is the share of asset i funded by debt (i.e. the quantity of debt). Expanding and in Equation (2):
We estimate the annualised monthly net return (NRit) that major banks could have earned on investing in: (i) repos priced at the Reserve Bank auction rate; (ii) Australian bank bills; and foreign exchange swaps where Australian dollars are lent against (iii) Japanese yen (JPY); and (iv) US dollars (USD). The sample window is monthly data from January 2008 to June 2019 (a total of 138 observations).
2.1 Gross Return on Money Market Investments
We first calculate the average monthly gross return (GRit) on each trade by averaging daily interest rates on the asset during the month. This allows us to match the monthly frequency of funding cost data, abstract from significant daily noise in the data, as well as focus on persistent deviations between interest rates in money markets and the more medium-term considerations that determine the structure of the balance sheet.[4]
We define the gross return on:
- Repos as the rate accepted by the Reserve Bank on one-month reverse repos at its open market operations.[5]
- Bank bills as the average three-month bank bill swap rate.
- Foreign exchange swaps as the implied rate of return from a three-month foreign exchange swap of Australian dollars (AUD) into the foreign currency. Specifically, it is the return earned from lending AUD against the foreign currency in the spot market, investing the foreign currency in three-month JPY or USD London Interbank Offered Rate (LIBOR), and swapping the proceeds back into AUD at the forward rate.
Until 2014, gross returns on money market trades were between 5 and 20 basis points higher than the unsecured overnight cash rate at which banks lend to each other, and traded in a narrow range (Figure 2). Since then, money market interest rates have persistently diverged.
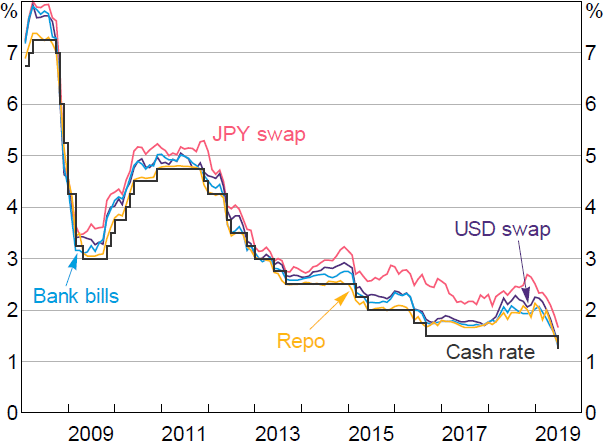
Sources: Bloomberg; RBA
2.2 Deriving Asset-specific Funding Costs
The debt funding rate (DFRt) is the weighted average cost of non-equity funding for major banks estimated by the Reserve Bank (Figure 3).[6] The DFRt moved broadly in line with the cash rate over the sample period. In 2008 and 2009, DFRt was generally lower than the cash rate. As risk was re-evaluated and competition for stable funding increased following the financial crisis, a repricing of longer-term debt and retail deposit rates occurred. As a result, total DFRt rose above the cash rate.[7]
We estimate the cost of equity from a Fama-French three-factor model, a dividend discount model (DDM) and a capital asset pricing model (CAPM). We take the simple average of these three estimates as the equity funding rate (EFRt) in our model (Figure 3). We average the estimates because, while all three models are commonly used, the literature is not unanimous on which method provides the best estimate of the cost of equity. As a crosscheck, we also derive a specification of the CAPM approach that uses a time-varying estimate of the market risk premium (see Section 4). Over the period, the equity funding rate reached almost 15 per cent at its peak and rose by 100 basis points to 12 per cent between 2015 and 2018, before declining in 2019. Noticeably, the spread between EFRt and DFRt widened following a broad repricing of risk in the post-crisis period. This implies that the relative cost of equity has increased over the sample period.
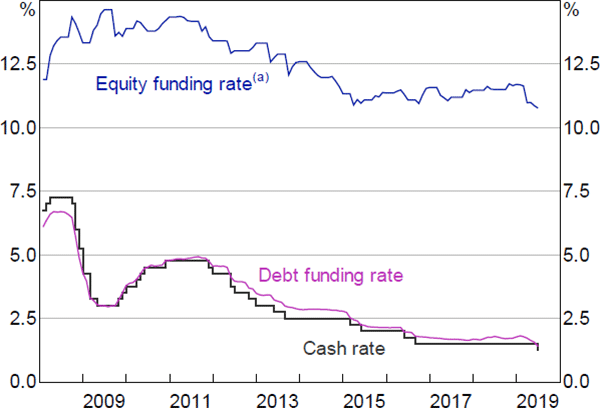
Note: (a) Arithmetic average of CAPM, DDM and Fama-French estimates
Sources: APRA; Authors' calculations; Bloomberg; RBA
Banks are generally required to fund riskier assets with a higher share of equity capital. Consequently, to derive the funding cost for a specific asset, we estimate the share of equity funding implicitly allocated to asset i (denoted by ). The methodology is complicated because the shares represented by are not directly observable. However, we do observe the target that banks set for their overall risk-weighted equity ratio:
We define as the average common equity Tier 1 risk-weighted capital ratio reported by the major banks in period t. Data for are only available since 2013. The back data are estimated by splicing back the Tier 1 capital ratio (Figure 4). We estimate that risk-weighted equity ratios have nearly doubled over the past 10 years as banks built up capital buffers following the financial crisis. This implies that, all else equal, banks funded total assets with around twice as much equity in 2018/19 than they did in 2008.
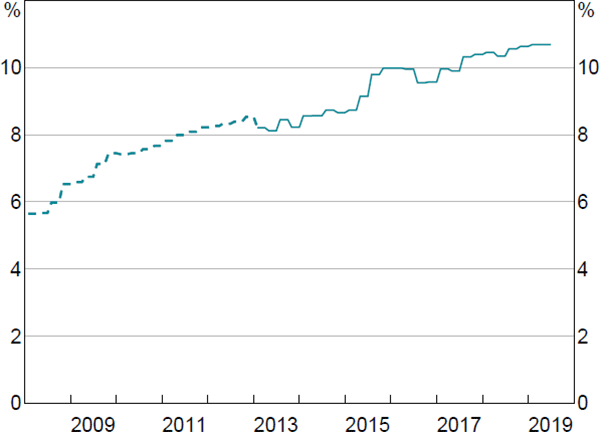
Note: Dashed line is spliced estimates using the Tier 1 capital ratio
Sources: APRA; Authors' calculations
Our approach uses the average to derive the value for .[8] We assume profit-maximising banks choose an optimal funding mix at the ‘aggregate’ balance sheet level, after taking into consideration return-on-equity targets and regulatory requirements.
The approach assumes that when investing in the marginal asset, banks tend to consider the risk-adjusted equity share of funding the asset as being the average that applies at the aggregate balance sheet level. If the marginal investment decision were based on a smaller share of equity capital funding than the average, it would imply higher profitability but an erosion of the target . On the other hand, if the marginal investment decision were based on a higher share of equity capital funding than the average, it would imply lower profitability but a higher-than-targeted . Therefore, we assume that, after accounting for risk, the marginal funding decision for each individual asset i is the same as the average funding decision implied at the balance sheet level:[9]
where Equityit is the value of common equity Tier 1 capital funding specifically attributed to asset i at time t, and Risk-weighted exposureit is the risk-weighted exposure to asset i at time t. The value of equity that is attributable to asset i (Equityit) is unobservable. We estimate the denominator of Equation (6) to derive Equityit. The risk-weighted exposure to asset i at time t, is calculated as the notional risk weight (wi) that applies to the asset, times the total value of the asset:[10]
We liaised with specialist teams at APRA to construct time-invariant stylised risk weights (wi) for each money market trade i in accordance with current Australian prudential standards. For any asset i at time t, the nominal share of equity funding is calculated as:
Recall, this is an estimate of the concept of introduced in Equation (3) earlier, but which was later noted as being an unobservable variable.
Footnotes
While the Modigliani-Miller theorem suggests that the funding mix should not affect the total cost of funding, we assume that the marginal costs of debt and equity are fixed at any given time (which would likely be the case if the debt and equity are raised before the asset allocation decision is made). Further, there is some evidence (e.g. Aboura and Lépinette 2015; Cline 2015) that Modigliani-Miller does not hold for banks. If this is true, banks should always prefer to minimise equity funding. [3]
An extension to our approach would be to use higher-frequency data to more accurately reflect the aspects involved in managing trading positions and address research questions related to day-to-day trading activity. However, we choose to strike a balance that more explicitly acknowledges broader balance sheet considerations relevant over the medium term. The main aim is not to capture a dynamic trading decision, which might be relevant at the margin over a shorter horizon. [4]
Note that this is not intended to suggest that private sector repos outside open market operations necessarily have the same return profile. The gross return on private sector repos might be significantly higher for a range of transactions not directly visible to the Reserve Bank due to the over-the-counter nature of the repo market. [5]
See Black and Titkov (2019) for the latest update on banks' funding costs calculated by the Reserve Bank. [6]
In the post-crisis period we would argue that the marginal and average cost of debt are equal. This is likely to be the case because banks are now required to demonstrate more stable sources of funds and probably have a target for the share of deposits in overall debt funding. [7]
This analysis focuses on risk-weighted capital constraints rather than the leverage ratio (which is not a risk-weighted constraint) because the Australian Prudential Regulation Authority (APRA) focuses on risk-weighted capital in its ‘unquestionably strong’ benchmark. Risk-weighted capital constraints are more binding for major banks than the leverage ratio (APRA 2018). [8]
Equation (6) is the asset-specific counterpart to the broader aggregated balance sheet Equation (5). [9]
Here we account for the difference between the notional dollar value of the asset and the institution's risk exposure to the asset. For bank bills, the notional and exposure values are identical, but they differ for hedged or collateralised trades such as repos and foreign exchange swaps. See the discussion in Section 4.3 for more details, including on the calibration of risk weights in the baseline results. [10]