Research Discussion Paper – RDP 2019-09 Australian Money Market Divergence: Arbitrage Opportunity or Illusion?
September 2019
1. Introduction
Short-term money markets primarily consist of unsecured cash market transactions, repurchase agreements (repos), bank bills and foreign exchange swaps. If markets are efficient and the risk characteristics of financial instruments are taken into account, there is no reason why the price of Australian dollar cash should differ across markets; that is, the law of one price should hold. Under these conditions, market participants would exploit deviations in interest rates if they represent a profit opportunity by borrowing in the market where rates are lowest and lending to the market where rates are higher, until it is no longer profitable to do so.
In recent years, however, interest rates in short-term money markets have significantly and persistently deviated from each other, and from overnight cash rate expectations as captured by overnight indexed swaps (Figure 1). A commonly cited example of this divergence is the Japanese yen basis, which has remained unusually wide for a number of years.[1]
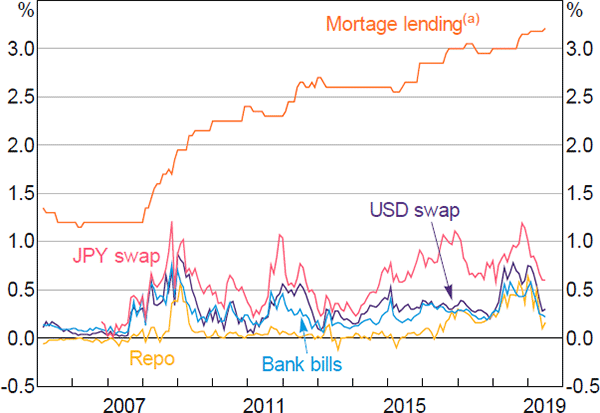
Note: (a) Discounted variable rates on owner-occupier housing loans; spread to cash rate
Sources: Bloomberg; RBA
The issue of unexploited arbitrage opportunities in foreign exchange markets and the breakdown of the covered interest parity condition has been well documented.[2] Possible explanations include increased demand to hedge US dollar exposures, changes which have reduced balance sheet capacity for such trades (Sushko et al 2016), increasingly segmented money markets, and greater heterogeneity in the funding costs of banks after accounting for risk and transaction costs (Rime, Schrimpf and Syrstad 2017).
We expand on this literature by estimating the average funding cost for major banks in Australia with respect to trading in short-term money markets. Similar to Boyarchenko et al (2018) whose work focuses on US money markets, our research examines the net returns from trades in different segments of domestic money markets. However, we go a step further and develop a novel approach to identify the cost of funding each money market trade.
This paper explores important reasons why the four major Australian banks have not transacted in a manner that would close the observed divergences between money market rates. Specifically, we estimate the profits major banks can earn on lending Australian dollar cash in the markets for repos, bank bills and foreign exchange swaps. To assess profitability we take into consideration how the major banks fund themselves. The cost of equity and non-equity funding both play an important role. Throughout, we refer to non-equity as ‘debt’, but note that it also includes deposits. The main finding is that the cost of funding trading positions with debt has not fallen as much in the low interest rate period as the available return in money markets. That is, the cost of debt funding has risen relative to the return that can be earned by investing in money markets. The relative cost of debt funding has not only eroded narrow trading margins, but has made such trades unprofitable over much of the past decade. In addition, in the post-2008 crisis period, increased equity funding has also weighed on profitability, particularly in bank bill and foreign exchange swap markets. It appears that, until recently, higher funding costs (debt and equity) have reduced the incentive to lend into money markets, despite the observed spread between interest rates.
We also compare returns on money market trades with returns earned by major banks on mortgage lending, to assess the opportunity cost of deploying their balance sheet to arbitrage differences in money market rates.
2. Estimating Funding Costs, Gross Returns and Net Returns
The net return (NRit) a bank earns on a position in an asset i at time t is calculated as the gross return (GRit) on the asset less the total cost of funding the position (TCit):
This methodology explicitly accounts for differences in asset-specific funding costs, which is important because prudential standards generally require banks to fund riskier assets with a higher share of equity capital (which is more expensive than debt).[3] Equation (1) can be rewritten to specifically account for the shares of total funding attributable to equity and debt :
The total cost of equity is calculated as * EFRt where EFRt is the equity funding rate (i.e. the price of equity funding) and is the portion of asset i funded by equity (i.e. the quantity of equity). Similarly, can be expressed as * DFRt where DFRt is the debt funding rate (i.e. the price of debt funding) and is the share of asset i funded by debt (i.e. the quantity of debt). Expanding and in Equation (2):
We estimate the annualised monthly net return (NRit) that major banks could have earned on investing in: (i) repos priced at the Reserve Bank auction rate; (ii) Australian bank bills; and foreign exchange swaps where Australian dollars are lent against (iii) Japanese yen (JPY); and (iv) US dollars (USD). The sample window is monthly data from January 2008 to June 2019 (a total of 138 observations).
2.1 Gross Return on Money Market Investments
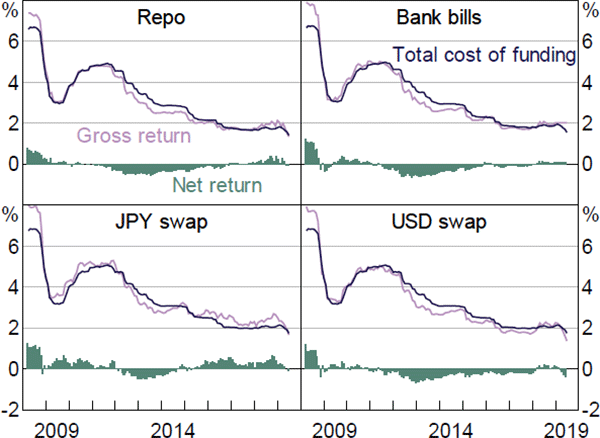
We first calculate the average monthly gross return (GRit) on each trade by averaging daily interest rates on the asset during the month. This allows us to match the monthly frequency of funding cost data, abstract from significant daily noise in the data, as well as focus on persistent deviations between interest rates in money markets and the more medium-term considerations that determine the structure of the balance sheet.[4]
We define the gross return on:
- Repos as the rate accepted by the Reserve Bank on one-month reverse repos at its open market operations.[5]
- Bank bills as the average three-month bank bill swap rate.
- Foreign exchange swaps as the implied rate of return from a three-month foreign exchange swap of Australian dollars (AUD) into the foreign currency. Specifically, it is the return earned from lending AUD against the foreign currency in the spot market, investing the foreign currency in three-month JPY or USD London Interbank Offered Rate (LIBOR), and swapping the proceeds back into AUD at the forward rate.
Until 2014, gross returns on money market trades were between 5 and 20 basis points higher than the unsecured overnight cash rate at which banks lend to each other, and traded in a narrow range (Figure 2). Since then, money market interest rates have persistently diverged.
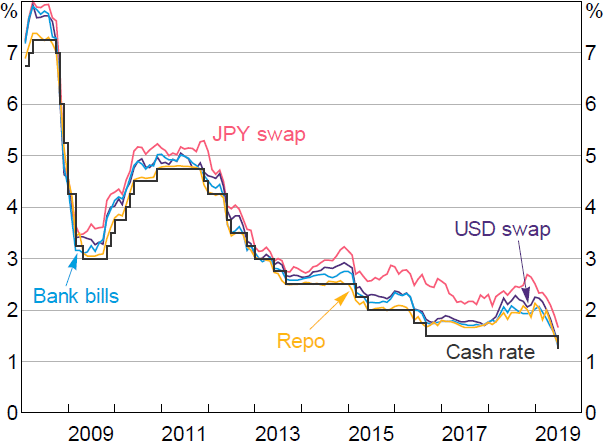
Sources: Bloomberg; RBA
2.2 Deriving Asset-specific Funding Costs
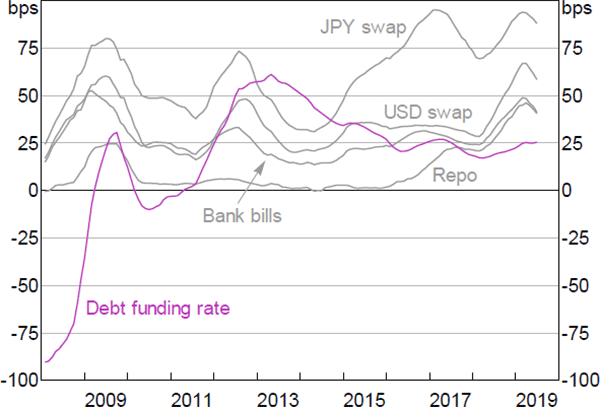
The debt funding rate (DFRt) is the weighted average cost of non-equity funding for major banks estimated by the Reserve Bank (Figure 3).[6] The DFRt moved broadly in line with the cash rate over the sample period. In 2008 and 2009, DFRt was generally lower than the cash rate. As risk was re-evaluated and competition for stable funding increased following the financial crisis, a repricing of longer-term debt and retail deposit rates occurred. As a result, total DFRt rose above the cash rate.[7]
We estimate the cost of equity from a Fama-French three-factor model, a dividend discount model (DDM) and a capital asset pricing model (CAPM). We take the simple average of these three estimates as the equity funding rate (EFRt) in our model (Figure 3). We average the estimates because, while all three models are commonly used, the literature is not unanimous on which method provides the best estimate of the cost of equity. As a crosscheck, we also derive a specification of the CAPM approach that uses a time-varying estimate of the market risk premium (see Section 4). Over the period, the equity funding rate reached almost 15 per cent at its peak and rose by 100 basis points to 12 per cent between 2015 and 2018, before declining in 2019. Noticeably, the spread between EFRt and DFRt widened following a broad repricing of risk in the post-crisis period. This implies that the relative cost of equity has increased over the sample period.
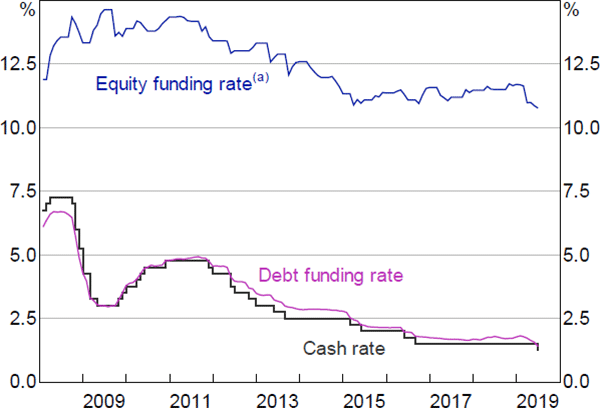
Note: (a) Arithmetic average of CAPM, DDM and Fama-French estimates
Sources: APRA; Authors' calculations; Bloomberg; RBA
Banks are generally required to fund riskier assets with a higher share of equity capital. Consequently, to derive the funding cost for a specific asset, we estimate the share of equity funding implicitly allocated to asset i (denoted by ). The methodology is complicated because the shares represented by are not directly observable. However, we do observe the target that banks set for their overall risk-weighted equity ratio:
We define as the average common equity Tier 1 risk-weighted capital ratio reported by the major banks in period t. Data for are only available since 2013. The back data are estimated by splicing back the Tier 1 capital ratio (Figure 4). We estimate that risk-weighted equity ratios have nearly doubled over the past 10 years as banks built up capital buffers following the financial crisis. This implies that, all else equal, banks funded total assets with around twice as much equity in 2018/19 than they did in 2008.
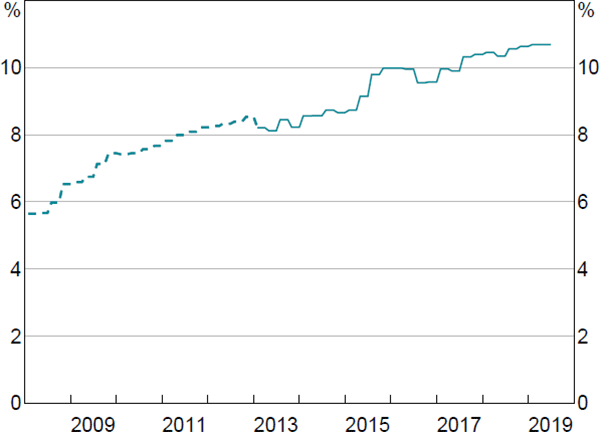
Note: Dashed line is spliced estimates using the Tier 1 capital ratio
Sources: APRA; Authors' calculations
Our approach uses the average to derive the value for .[8] We assume profit-maximising banks choose an optimal funding mix at the ‘aggregate’ balance sheet level, after taking into consideration return-on-equity targets and regulatory requirements.
The approach assumes that when investing in the marginal asset, banks tend to consider the risk-adjusted equity share of funding the asset as being the average that applies at the aggregate balance sheet level. If the marginal investment decision were based on a smaller share of equity capital funding than the average, it would imply higher profitability but an erosion of the target . On the other hand, if the marginal investment decision were based on a higher share of equity capital funding than the average, it would imply lower profitability but a higher-than-targeted . Therefore, we assume that, after accounting for risk, the marginal funding decision for each individual asset i is the same as the average funding decision implied at the balance sheet level:[9]
where Equityit is the value of common equity Tier 1 capital funding specifically attributed to asset i at time t, and Risk-weighted exposureit is the risk-weighted exposure to asset i at time t. The value of equity that is attributable to asset i (Equityit) is unobservable. We estimate the denominator of Equation (6) to derive Equityit. The risk-weighted exposure to asset i at time t, is calculated as the notional risk weight (wi) that applies to the asset, times the total value of the asset:[10]
We liaised with specialist teams at APRA to construct time-invariant stylised risk weights (wi) for each money market trade i in accordance with current Australian prudential standards. For any asset i at time t, the nominal share of equity funding is calculated as:
Recall, this is an estimate of the concept of introduced in Equation (3) earlier, but which was later noted as being an unobservable variable.
3. Estimation Results
We estimate the net return the major banks could earn on each money market trade for every month from January 2008 to June 2019 (see Table A1 for a data summary). By substituting for in Equation (4), the net return on asset i at time t is given by:
Most of the variation in the total cost of funding money market positions has been due to developments in debt funding. The total cost of debt has fallen significantly since 2008 (Figure 5). This decline can be attributed to the fall in the average interest rate payable on debt. At the beginning of the sample, the debt funding rate was well below the cash and other money market rates (Figure 6). While the debt funding rate has broadly moved lower in absolute terms over the period in line with the stance of monetary policy, it was around 25 basis points higher than the cash rate during 2018, reflecting that there was less than full pass-through. The increase in the debt funding spread to cash was largely due to competition for deposits and longer-term debt following the financial crisis (Atkin and Cheung 2017).
Trends in the total cost of funding positions have been similar in all four money markets but the composition has changed noticeably (Figure 5). At the same time as the total cost of funding debt declined by around 500 basis points, the total cost of equity rose marginally. This was mainly due to increased equity funding. In the repo market this has not had any material consequences since positions are funded with almost no equity at all. The higher risk profile of bank bills relative to collateralised trades, such as repos, makes equity funding a little more important for investing in this market. However, because under our methodology foreign exchange swaps attract a relatively high risk weight (based on prudential standards), the role of equity funding is much more important for these positions. Equity accounted for around 20 per cent of the total cost of funding these assets by 2018, up from around 5 per cent in 2008.
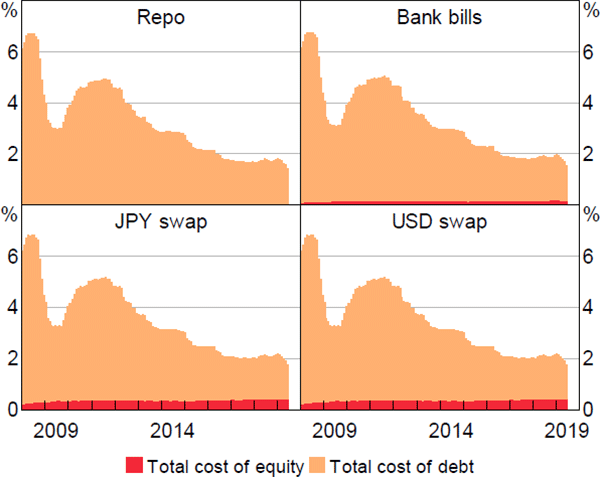
Sources: APRA; Authors' calculations; Bloomberg; RBA
Sources: Authors' calculations; Bloomberg; RBA
During the first half of 2008, major banks could earn a net return on investing in bank bills and foreign exchange swaps of around 110 basis points, and around 60 basis points on repo (Figure 7). The profitability of money market trades declined in the second half of 2008 and net returns have generally been negative (or marginally positive) since 2011. Two main developments have driven this result. The cost of debt has risen relative to gross returns. At the same time, the proportion of more expensive equity funding has increased.
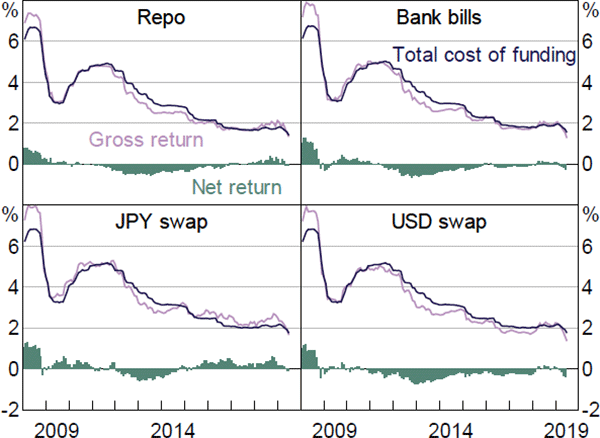
Sources: APRA; Authors' calculations; Bloomberg; RBA
The increase in the repo rate during 2018 made lending cash under repo only marginally profitable. The repo spread to cash averaged around 40 basis points, but the net return from lending under repo is estimated to have been less than 20 basis points. Bank bill rates also rose over this period, but not sufficiently to make investing in bills a profitable money market trade. Gross returns from lending Australian dollar cash in the foreign exchange swap market also rose in 2018. The bases measured in both USD and JPY have persisted since 2014. Relative to cash rate expectations, the gross return on USD swaps increased to 60 basis points. However, under our methodology, the net return of lending cash under USD swap remains close to zero. This outcome is due to swaps being attributed higher risk weights, resulting in a larger share of equity funding. The gross return on JPY swaps also increased to 90 basis points relative to cash rate expectations. Under our methodology this has been associated with positive net returns from lending Australian dollar cash into the JPY swap market of around 30 basis points. Subsequently in 2019, net returns in all these money markets declined as the spread between money market rates and cash rate expectations narrowed.
Our results do not in any way address whether banks are less active as market makers for customers who continue to take investment positions. Nor should the approach be interpreted as suggesting that the major banks have no position at all in money markets.
4. Sensitivity Analysis
In this section we test the sensitivity of the outputs to the key assumptions of the model in order to test the robustness of our findings.
4.1 Debt Funding Rate
The decline in net returns from money market investments, attributable to the narrowing in the spread between gross returns and the average debt funding rate, is a key result of our methodology.
In the baseline derived above, we defined the debt funding rate as the average of all debt (non-equity) sources. This assumes that all investment activity is funded at the aggregated balance sheet level. We believe this reflects how the major banks broadly manage their balance sheet composition and compliance with prudential standards. For example, equity is raised based on the aggregate balance sheet requirement. However, this is not an entirely accurate description of how banks operate their individual business lines on a day-to-day basis. Money market desks typically either source marginal funding externally or are charged an overlay fee for funding sourced internally (i.e. transfer price).[11] Therefore, the debt funding rate faced by the relevant money market desk might differ from the rate we derive in preceding sections.
To test the sensitivity of net returns from money market investments to a different mix of funding rates, we consider two scenarios and compare them to the baseline results derived above. Both relax the assumption that the average debt funding rate is the relevant input into the calculation of net returns. Instead, debt funding for these money market investments is externally sourced in a market where interest rates are relatively low. The share of equity funding these investments remains unchanged from the baseline.
In the first instance, we make the deliberately extreme assumption that investments can be funded at the overnight cash rate target. In recent years this assumption improves net returns relative to the baseline (Figure 8). Between 2016 and 2018, borrowing at the cash rate and lending into the repo market, the bank bill market, or foreign exchange swaps (JPY or USD), improved on baseline net returns by around 20 basis points. Notably, even when funded at the cash rate, foreign exchange swaps directed into USD were not profitable for the supervised major banks until forward rates began to rise substantially in 2018. However, these results are upwardly biased because funding at the cash rate implies lower costs than any of the accessible money market alternatives.
In the second scenario, we test the sensitivity of the baseline results to a switch in funding to the repo market. Borrowing under repo to lend into the repo market is a zero-sum game. Net returns from borrowing under repo to lend cash into the bank bill market remained negative in 2018. The relative riskiness of the trade implies the use of more equity funding and in the second half of 2018 the repo rate was higher than the bank bill rate. The implication is that there has been insufficient economic incentive to arbitrage between the two markets. Similarly, borrowing in the repo market to lend cash under swap in USD does not appear to have been a profitable investment for the major banks since around the beginning of the sample. For repo funding to yield a positive net return from money market investment requires surprisingly wide spreads such as those observed in the JPY foreign exchange swap market. The net return for major banks borrowing under repo to lend into the JPY swap market peaked at around 50 basis points before narrowing to around 15 basis points for most of 2017–18 and becoming negative since late 2018. This finding also further substantiates the link between the repo rate and foreign exchange swap rates described in Becker and Rickards (2017), whereby non-resident investors borrow in the repo market in order to take advantage of the basis trade.
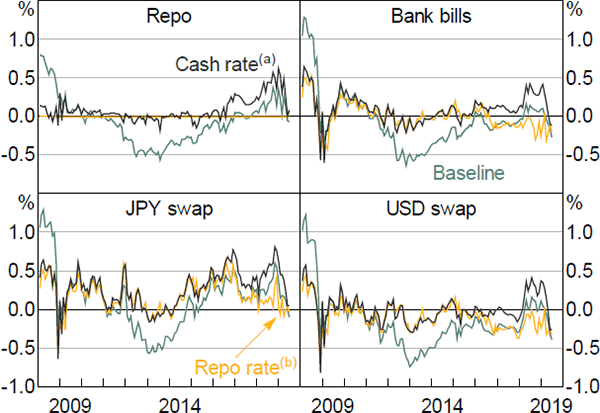
Notes:
(a) Assumes that debt is funded at the cash rate
(b) Assumes that debt is funded at the repo rate
Sources: APRA; Authors' calculations; Bloomberg; RBA
Our approach does not measure the degree to which arbitrage is already reflected in observed money market rates. That is, it could be possible that arbitrage activity has led to a convergence between funding and investment rates so as to exhaust profitable trading opportunities. Some of the changing dynamics in money markets in 2018, where repo, bank bill and foreign exchange swap rates have become more volatile and correlated, may in part be explained by the return to slightly more favourable net returns as described in this paper. However, the methodology is a useful framework to explain why there is not complete convergence between market rates.
4.2 Equity Funding Rate
To test the sensitivity of our results to the equity funding rate we also derive an additional estimate from a specification of the CAPM approach. We assume investors adaptively base their expectations of market risk premia on trends observable in the recent past. Specifically, we calculate the market risk premium at time t as the difference between the average annual return on the All Ordinaries Index of equities over the past 15 years and the yield on 10-year Australian Government securities. This calibration is very sensitive to past market movements (and in particular, the sharp price falls that occurred during the financial crisis) and may be a downward-biased estimate of the equity funding rate. Nonetheless, our results remain largely unchanged from the baseline under this approach (Figure 9).
Sources: APRA; Authors' calculations; Bloomberg; RBA
4.3 Risk Weights
The amount of equity required to fund a money market investment is determined by its risk weight. The risk weight is calibrated according to the likelihood and magnitude of potential losses on an investment. Intuitively, trades that are less risky attract lower risk weights. In our analysis, risk weights are driven by two key factors (Table 1). First, the creditworthiness of the borrower is a proxy for their ability to repay the loan at maturity. Lending cash to a borrower with a higher credit rating increases the likelihood of full repayment at maturity and is associated with a lower risk weight. Second, loan collateralisation reduces the risk exposure to the borrower. If the borrower defaults, the cash lender may recoup most (or all) of their investment by selling the collateral. As such, less of their investment is ‘at risk’ and this is associated with a lower risk weight.
| Transaction and borrower characteristics | Probability of default | Loss given default | Likelihood of losses | Size of risk weight |
|---|---|---|---|---|
| Uncollateralised transaction (e.g. bank bills) |
||||
| AA-rated borrower | Lower | High | Lower probability of high losses | Small |
| BBB-rated borrower | Higher | High | Higher probability of high losses | Large |
| Collateralised transaction (e.g. repo) |
||||
| AA-rated borrower | Lower | Low | Lower probability of low losses | Very small |
| BBB-rated borrower | Higher | Low | Higher probability of low losses | Very small |
|
Sources: APRA; Authors' calculations |
||||
Consider two stylised examples to demonstrate how the creditworthiness of the cash borrower and the collateralisation affect the risk weight on an investment. In both examples Bank A is seeking to invest cash for three months.
Bank A can lend the cash on an uncollateralised basis by buying a bank bill issued by Bank B. Bank A is exposed to default on the whole face value of the bank bill. The likelihood of this occurring varies with the creditworthiness of Bank B (the borrower). Therefore, the risk weight on unsecured transactions can vary from low (if the borrower is highly rated) to high (if the borrower has a low credit rating), reflecting the expected loss on the investment. Risk weights on uncollateralised trades vary significantly depending on the creditworthiness of the borrower.
Alternatively, Bank A can collateralise its investment by lending to Bank B under repo. Collateralisation significantly reduces the likelihood – and magnitude – of potential losses. If Bank B defaults, Bank A can sell the collateral to recoup their investment. As a result, risk weights on collateralised trades tend to be lower.
Due to the large variation in possible risk weights, we evaluate the sensitivity of our results to changes in risk weights (Figure 10). We use baseline assumptions for risk weightings where domestic investments are AA-rated (in line with the major banks in Australia), and foreign investments are A-rated to reflect lower credit worthiness (e.g. Japanese banks).
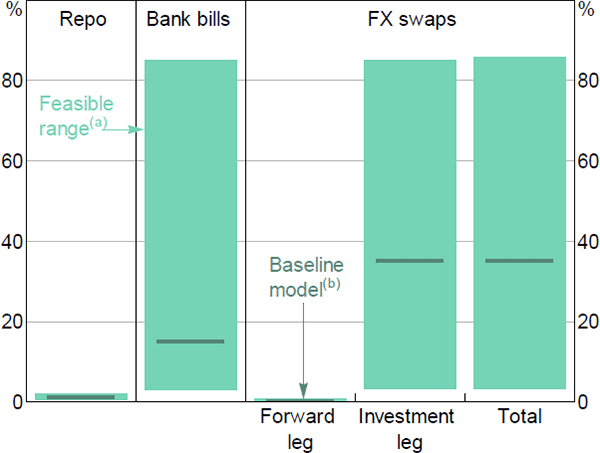
Notes:
(a) Based on counterparty credit rating, from AA (lowest risk weight) to BBB (highest risk weight) and
possible treatment under Trading Book and Banking Book
(b) Based on AA rating for repo and bank bills; and A rating for foreign exchange swaps
Sources: APRA; Authors' calculations; RBA
Figure 11 depicts the possible dispersion in net returns when allowing risk weights to vary. For repo transactions, the range of possible risk weights is narrow since collateralisation reduces the risk exposure of the investor. As a result, net returns do not vary widely with a change in borrower credit rating. In contrast, where the investment is uncollateralised (such as bank bills), the range of possible net returns becomes much wider. For investments involving bank bills (domestic or foreign under swap) we find the net return becomes more negative as borrower creditworthiness deteriorates and the risk weight increases. As the creditworthiness of the borrower improves for swaps into USD, net returns improve but typically remain negative. Over recent years, the baseline net return on JPY swaps would have remained positive even if risk weightings had increased significantly.
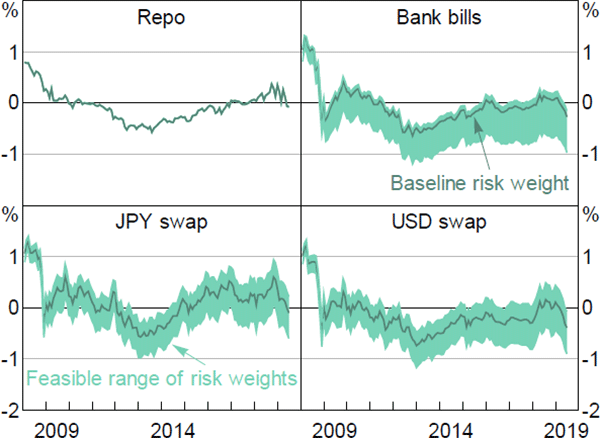
Note: See notes to Figure 10
Sources: APRA; Authors' calculations; Bloomberg; RBA
4.4 Leverage Ratio Considerations
The leverage ratio constrains the amount of debt financing that banks can take on by setting the minimum equity to be held against total assets. Consequently, it also limits the scope banks have to lower their funding costs by substituting relatively cheap debt for equity. Prudential standards require banks to fund total assets with at least 3 per cent of ‘Tier 1’ equity capital.[12] Currently, the leverage ratios of major banks in Australia are significantly above this regulatory minimum so as not to be a binding constraint.
However, the leverage ratio could constrain arbitrage at the margin by limiting the ability of banks to take on the significant amounts of additional leverage that might be required to close the spreads observable to date. There might also be a reluctance, even at the conservative leverage positions, for any one bank to take on significantly more debt than its peers.
5. Leverage, Profitability and the Consequences for Money Markets
We use the results derived in the previous sections to describe the funding structure of an investment and its profitability. Figure 12 graphs the profitability of a foreign exchange swap funded under repo on the y-axis, and its funding mix on the x-axis. The funding composition is measured by the debt-to-equity ratio. We define the break-even frontier as the minimum spread required between gross returns on a foreign exchange swap and the repo rate for the investment to break even (i.e. cover the associated cost of equity). This implies that, for a given level of leverage, the spread must be on the frontier or higher for the investment to be viable. The break-even frontier is convex to the origin and increases exponentially as the debt-to-equity ratio approaches zero. Intuitively, as investments get funded with greater amounts of relatively expensive equity, the minimum spread required for a foreign exchange swap to break even widens to cover the increase in funding costs. If a foreign exchange swap were fully funded by equity, the minimum break-even spread would converge to the difference between the cost of equity and the repo rate. If a foreign exchange swap were entirely funded through repo, the break-even spread would be zero (i.e. this trade would be profitable when the return on swaps is at least as high as the cost of funding the trade in repo).
Prior to the financial crisis, foreign exchange swaps required a minimum spread of around 15 basis points to break even at the estimated debt-to-equity ratio at that time (point A, Figure 12). At the debt-to-equity ratio of around 50, this implies the foreign exchange swap was being funded with approximately 2 per cent equity and 98 per cent debt. In 2018, the minimum spread required by banks to break even on foreign exchange swaps increased to around 35 basis points (point B, Figure 12). This reflects two developments. First, the entire break-even frontier shifted upwards due to the increase in the relative cost of equity over the period. For any given degree of leverage, this implies that the minimum break-even spread is higher than in 2008. Second, the debt-to-equity ratio for foreign exchange swaps has almost halved over the period, moving the break-even point left along the frontier. For every dollar of equity funding the swap, we estimate that the swap is funded by $25 of debt funding in 2018. This is consistent with a leverage ratio of just under 4 per cent. Effectively, the hurdle to achieve profitable arbitrage has been raised substantially.
Major banks were important providers of liquidity in money markets prior to the financial crisis. Since then, a reduced tolerance for risk has diminished the ability and willingness of banks to engage in either proprietary trading or market-making activities (CGFS 2014; ASIC 2018). Since 2008, net returns on money market investments have declined, and are either negative or close to zero if they are funded in the repo market. Our results support the idea that major banks have a reduced incentive to lend in money markets, and may help to explain the persistent price divergence across money markets.
If banks no longer have an incentive to arbitrage, then are there any participants whose funding structure permits arbitrage? In the domestic repo market, around half the cash lent by dealers is borrowed by non-residents. Some of these borrowers are likely to be non-banks which might be better able to take advantage of arbitrage opportunities across money markets, as they are typically not bound by leverage and capital requirements to the same extent as banks. We observe repo rates co-moving with the JPY basis in recent years where the repo-funded yen basis trade has remained marginally profitable. This may indicate non-bank institutions have been bidding up the repo rate to the point where the yen basis trade is no longer a viable investment strategy from the aggregate balance sheet perspective of a bank.
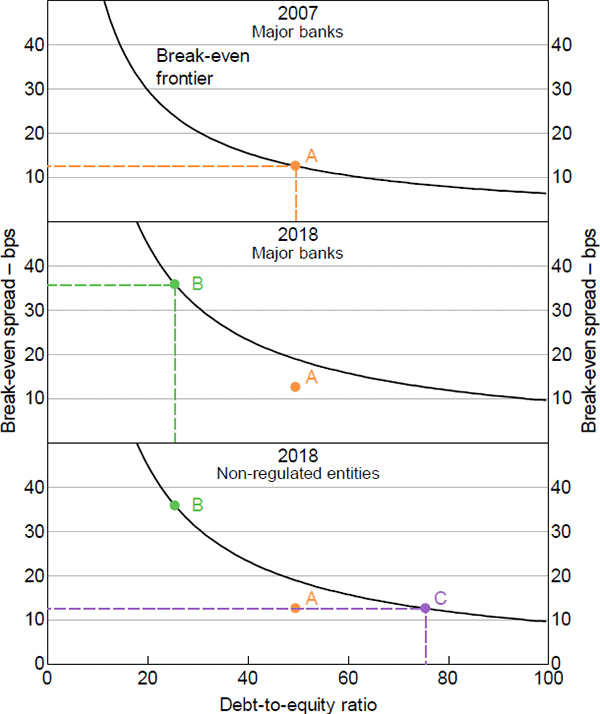
Sources: APRA; Authors' calculations; RBA
Consider the case of a non-regulated entity seeking to arbitrage across the repo and foreign exchange swap markets. How would this foreign exchange swap need to be funded in order for break-even spreads to return to pre-crisis levels (point C, Figure 12)? In order to return a profit for an institution that exhibits the same funding costs as a major bank, the foreign exchange swap must be funded by a debt-to-equity ratio of more than 75. This corresponds to a leverage ratio of approximately 1.3 per cent. This is well below the regulatory minimum of 3 per cent stipulated by current prudential standards applicable to supervised banking institutions. Consequently, only entities not regulated by prudential standards would have the capacity to leverage up to this extent. This result is based on a break-even frontier which is a function of banks' equity costs. However, the cost of equity faced by a highly leveraged non-regulated entity is likely to be much higher than the cost of equity depicted for a prudentially regulated bank. If this is the case, then the break-even frontier depicted in Figure 12 would shift upwards, and the minimum break-even spread required would widen. Consequently, even our framework underestimates the degree of leverage non-regulated entities would require for arbitrage investments to be profitable.
Non-regulated entities have more flexibility in taking on leverage because they do not face regulatory minimum equity requirements. However, constraints on the balance sheets of the regulated banking sector may also limit arbitrage activities of non-regulated entities who rely on lines of credit from major banks. This is because the ability of banks to lend funds to these institutions will be dependent on regulatory requirements. In the United States, Boyarchenko et al (2018) suggests restrictions applying to broker-dealers have spilled over to non-regulated entities because regulated institutions are less willing to extend credit than in the past. Consequently, this has affected the ability of non-regulated entities to pursue arbitrage opportunities. It is difficult to assess the extent to which funding to non-regulated entities may have been constrained in the Australian context. However, it is possible that bank lending volumes to non-regulated entities in the domestic repo market are too small to close persistent money market arbitrage opportunities (Becker and Rickards 2017).
6. Opportunity Cost of Money Market Lending
A final consideration is whether there are more profitable uses for bank funding. We compare returns on money market trades with residential mortgages, the core business activity of major banks, to assess the opportunity cost of deploying their balance sheet to arbitrage differences in money market rates. Applying the same methodology, we find margins on residential mortgages have been significantly wider than those on money market trades during the sample period (Figure 13).[13] This suggests there is a significant opportunity cost associated with deploying equity funding away from mortgages and towards low-margin activities such as money market trading. Note, however, that there are fixed and variable costs – such as branches, personnel, information technology and other costs (including fees and commissions) – that banks face in writing mortgages which are not explicitly accounted for in our framework.[14] Some sources of revenue are also omitted, such as fees, charges and the revenue earned from market-making activities.
Different constraints apply to foreign banks operating in Australia. This affects their trading activities and is reflected in their balance sheets. Foreign banks (either through their branches or subsidiaries) tend to have smaller mortgage books and so might face a lower opportunity cost of arbitraging price differences in money markets. However, research suggests that the ability of large global banks to arbitrage across money markets may be constrained by various regulatory rules (see Boyarchenko et al (2018) for US banks and Aldasoro, Ehlers and Eren (2018) for European and, indirectly, Japanese banks). This may be an even more binding constraint than for the major Australian banks.
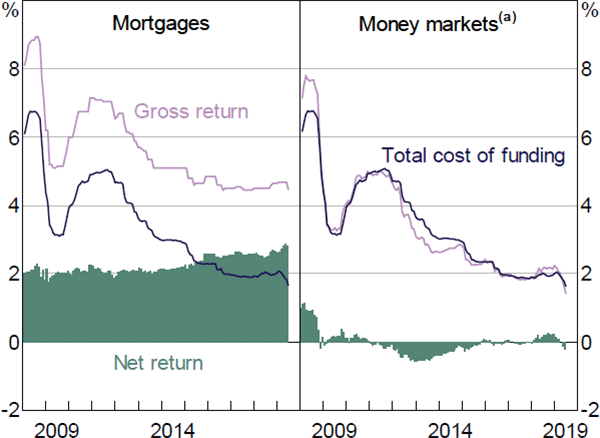
Note: (a) Average of estimates for bank bills, repos and swaps into JPY and USD
Sources: APRA; Authors' calculations; Bloomberg; RBA
More broadly, a reassessment of how banks optimise both capital and liquidity has meant that banks must utilise an internal liquidity transfer pricing model which fully reflects the cost of obtaining equivalent liquidity externally. A transfer pricing model which appropriately reflects funding costs will affect profit allocation and disincentivise activity of less profitable business units, such as money market trading desks. In the United Kingdom, banks surveyed by the Prudential Regulation Authority have revealed a more prominent role for capital efficiency in determining how banks assess business unit performance against other strategies (Bajaj et al 2018).
7. Conclusion
Opportunities to arbitrage across Australian money markets have seemingly widened and remained persistent in recent years. However, using a broad and comprehensive methodology for evaluating such opportunities indicates that arbitrage trades would have generally been unprofitable for major Australian banks. Once asset-specific funding costs are taken into account, or if money market desks are self-funded, profit opportunities are less apparent. An increase in debt funding costs relative to the cash rate has been a significant driver in reducing profitability of money market trades. A higher proportion of equity funding (which is more costly than debt) has also been a factor. Furthermore, there is a significant opportunity cost involved in undertaking money market trades when compared with higher-return business activities, such as lending for residential housing. This is reflected in the large share of mortgage and commercial loans that characterises the balance sheets of the major banks.
Consequently, money market rates may continue to diverge unless arbitrage becomes more profitable for banks, or non-bank participants replace banks as the principal arbitrageurs in these markets.
Appendix A: Data Summary
| Series | Series description | Source | Notes |
|---|---|---|---|
| Gross returns (GRit) | |||
| Mortgages | Discounted variable lending rate on housing loans | RBA statistical table F5 ‘Lending Rates’ | |
| Repurchase agreement | Repo rate (1 month bucket) from open market operations | RBA | |
| Japanese yen swap | Implied return rate from hedged 3-month swap of AUD into JPY |
Bloomberg | We assume the JPY leg is invested in Japanese LIBOR (3-month) |
| US dollar swap | Implied return rate from hedged 3-month swap of AUD into USD |
Bloomberg | We assume the USD leg is invested in US LIBOR (3-month) |
| Bank bills | 3-month bank bill swap rate | ASX; RBA | |
| Risk weights (wt) | |||
| Bank bills, foreign exchange swaps, repos, mortgages | Estimated | APRA | Stylised risk weights |
| CET1 capital ratio | |||
| Reported CET1 capital ratio | CET1 capital / risk exposure | APRA form ARF_110_0_1 | CET1 capital ratios are only available from 2013:Q1, back history is estimated by splicing Tier 1 capital ratio |
| Cost of funding | |||
| Debt (DFRit) | Cost of debt for Australian major banks | Black and Titkov (2019) | Includes deposit funding |
| Equity (EFRit) | Cost of equity for Australian major banks | Bloomberg | Arithmetic average of CAPM, DDM and Fama-French estimates |
References
Aboura S and E Lépinette (2015), ‘Do Banks Satisfy the Modigliani-Miller Theorem?’, Economics Bulletin, 35(2), pp 924–935.
Aldasoro I, T Ehlers and E Eren (2018), ‘Global Banks, Dollar Funding, and Regulation’, BIS Working Papers No 708, rev May 2019.
APRA (Australian Prudential Regulation Authority) (2018), ‘Leverage Ratio Requirement for Authorised Deposit-Taking Institutions’, Response to Submissions, 27 November.
ASIC (Australian Securities and Investment Commission) (2018), ‘High-Frequency Trading in Australian Equities and the Australian–US Dollar Cross Rate’, Report 597.
Atkin T and B Cheung (2017), ‘How Have Australian Banks Responded to Tighter Capital and Liquidity Requirements?’, RBA Bulletin, June, pp 41–50.
Bajaj R, A Binmore, R Dasgupta and Q-A Vo (2018), ‘Banks' Internal Capital Markets: How Do Banks Allocate Capital Internally?’, Bank of England Quarterly Bulletin, Q2.
Becker C, A Fang and JC Wang (2016), ‘Developments in the Australian Repo Market’, RBA Bulletin, September, pp 41–46.
Becker C and P Rickards (2017), ‘Secured Money Market Transactions: Trends in the Australian Repo Rate’, Paper presented at the 22nd Melbourne Money & Finance Conference ‘Evolutionary Trends in the Australian Financial Sector’, Hosted by the Australian Centre for Financial Studies, Melbourne, 10–11 July.
Black S and D Titkov (2019), ‘Developments in Banks' Funding Costs and Lending Rates’, RBA Bulletin, March, viewed 14 August 2019. Available at <https://www.rba.gov.au/publications/bulletin/2019/mar/developments-in-banks-funding-costs-and-lending-rates.html>.
Borio C, R McCauley, P McGuire and V Sushko (2016), ‘Covered Interest Parity Lost: Understanding the Cross-Currency Basis’, BIS Quarterly Review, September, pp 45–64.
Boyarchenko N, TM Eisenbach, P Gupta, O Shachar and P Van Tassel (2018), ‘Bank-Intermediated Arbitrage’, Federal Reserve Bank of New York Staff Report No 858, rev July 2018.
CGFS (Committee on the Global Financial System) (2014), Market-Making and Proprietary Trading: Industry Trends, Drivers and Policy Implications, CGFS Papers No 52, Bank for International Settlements, Basel.
Cline WR (2015), ‘Testing the Modigliani-Miller Theorem of Capital Structure Irrelevance for Banks’, Peterson Institute for International Economics Working Paper WP 15-8.
Debelle G (2010), ‘The Financial Situation Three Years On’, Address given at the Westpac Macro Strategy Forum, Sydney, 9 September.
Debelle G (2017), ‘How I Learned to Stop Worrying and Love the Basis’, Dinner Address given at the BIS Symposium ‘CIP ‐ RIP?’, Basel, 22–23 May.
Du W, A Tepper and A Verdelhan (2018), ‘Deviations from Covered Interest Rate Parity’, The Journal of Finance, 73(3), pp 915–957.
RBA (Reserve Bank of Australia) (2014), ‘Box B: Australian Major Banks' Cost-to-Income Ratios’, Financial Stability Review, September, pp 35–38.
RBA (2018), ‘Operations in Financial Markets’, Annual Report, pp 53–70.
Rime D, A Schrimpf and O Syrstad (2017), ‘Segmented Money Markets and Covered Interest Parity Arbitrage’, BIS Working Papers No 651.
Sushko V, C Borio, R McCauley and P McGuire (2016), ‘The Failure of Covered Interest Parity: FX Hedging Demand and Costly Balance Sheets’, BIS Working Papers No 590.
Wakeling D and I Wilson (2010), ‘The Repo Market in Australia’, RBA Bulletin, December, pp 27–35.
Acknowledgements
The paper has benefited from initial conceptual discussions with Chris Becker and was further developed in a series of internal Reserve Bank seminars. We also thank Andrew Alexandratos, Samuel Chui, Anthony Coleman and Justin Wang from the Australian Prudential Regulation Authority for their insights and useful advice on the application of regulatory aspects in this paper. The views expressed in this paper are our own and do not necessarily reflect those of the Reserve Bank of Australia or the Australian Prudential Regulation Authority. Any remaining errors are our own.
Footnotes
For more information on the Japanese yen basis, see Debelle (2017). The return enhancement offered by the persistently wide basis is regularly utilised by the Reserve Bank in its liquidity management operations (RBA 2018). However, the central bank does not face the same constraints as private market participants who are less inclined to enter the arbitrage trade. [1]
See Becker, Fang and Wang (2016), Becker and Rickards (2017), Borio et al (2016), Debelle (2010, 2017), as well as Du, Tepper and Verdelhan (2018). [2]
While the Modigliani-Miller theorem suggests that the funding mix should not affect the total cost of funding, we assume that the marginal costs of debt and equity are fixed at any given time (which would likely be the case if the debt and equity are raised before the asset allocation decision is made). Further, there is some evidence (e.g. Aboura and Lépinette 2015; Cline 2015) that Modigliani-Miller does not hold for banks. If this is true, banks should always prefer to minimise equity funding. [3]
An extension to our approach would be to use higher-frequency data to more accurately reflect the aspects involved in managing trading positions and address research questions related to day-to-day trading activity. However, we choose to strike a balance that more explicitly acknowledges broader balance sheet considerations relevant over the medium term. The main aim is not to capture a dynamic trading decision, which might be relevant at the margin over a shorter horizon. [4]
Note that this is not intended to suggest that private sector repos outside open market operations necessarily have the same return profile. The gross return on private sector repos might be significantly higher for a range of transactions not directly visible to the Reserve Bank due to the over-the-counter nature of the repo market. [5]
See Black and Titkov (2019) for the latest update on banks' funding costs calculated by the Reserve Bank. [6]
In the post-crisis period we would argue that the marginal and average cost of debt are equal. This is likely to be the case because banks are now required to demonstrate more stable sources of funds and probably have a target for the share of deposits in overall debt funding. [7]
This analysis focuses on risk-weighted capital constraints rather than the leverage ratio (which is not a risk-weighted constraint) because the Australian Prudential Regulation Authority (APRA) focuses on risk-weighted capital in its ‘unquestionably strong’ benchmark. Risk-weighted capital constraints are more binding for major banks than the leverage ratio (APRA 2018). [8]
Equation (6) is the asset-specific counterpart to the broader aggregated balance sheet Equation (5). [9]
Here we account for the difference between the notional dollar value of the asset and the institution's risk exposure to the asset. For bank bills, the notional and exposure values are identical, but they differ for hedged or collateralised trades such as repos and foreign exchange swaps. See the discussion in Section 4.3 for more details, including on the calibration of risk weights in the baseline results. [10]
In order to disincentivise the use of internal funding for trading activities, treasuries may set the debt funding cost applicable to money market trades higher than the average debt funding rate (Wakeling and Wilson 2010). [11]
APRA (2018) announced plans to increase this requirement to 3.5 per cent for banks using the internal ratings-based approach. [12]
Banks report the cost of funding new mortgages to APRA every month, which we use to evaluate our estimate of TCit for mortgages. Our calculated measure follows the same trends as the reported series but is consistently lower. This suggests that TCit is a conservatively low estimate of the actual total cost of funding mortgages. While it is difficult to draw conclusions on the bias, this gives us confidence that our approach does not over-inflate the cost of funding. [13]
For further discussion on the cost-to-income ratios of Australian banks, see RBA (2014). [14]