RDP 2019-06: The Effect of Mortgage Debt on Consumer Spending: Evidence from Household-level Data 7. Implications for Aggregate Household Spending
July 2019
- Download the Paper 1,513KB
The results so far provide some evidence for the debt overhang effect at the household level. A key question for policymakers is whether the results generalise to the aggregate level. Few papers have attempted to infer the aggregate implications from higher debt on spending, with the exception of Bunn and Rostom (2015). In this section, we use our preferred estimates from the FE model to draw some conclusions about the potential aggregate implications. We conduct two thought experiments. In the first experiment we use macro data and ask what aggregate consumption would have looked like had household debt remained at its 2006 level. In the second experiment we use our household-level data and compare actual spending of households in 2010 to their spending had their debt level remained at its 2006 level.
There are several limitations of these approaches and the estimates should be used as a rough guide only. Both experiments identify a partial effect of debt on aggregate spending. In particular, we only capture the (negative) effect on spending of home buyers that take on new mortgage debt but do not capture the (positive) spending response of the seller. But, if one household is buying a house for the first time or trading-up to a larger, more expensive house, often another household is on the other side of the transaction and selling their existing house. This household is liquidating their housing wealth. While the seller may invest in another house again, some share of the liquidated wealth will likely end up in consumption at some point, thereby lifting aggregate spending.[21] Mortgage-financed housing demand may further stimulate construction and, in consequence, lift aggregate consumption. Additionally, an increase in demand for mortgages should raise mortgage interest rates (all else equal). This could induce saving by other households and increase the returns to lenders. Finally, for both thought experiments we do not allow the sensitivity of spending to debt to vary across households.[22] Moreover, for the first thought experiment we assume that the aggregate effect of higher debt does not depend on the distribution of that debt, or that distribution, to change over time.
7.1 Using Macro Data
Using macro data allows us to gauge the aggregate effect of debt on consumption beyond the HILDA Survey sample period. Our elasticity estimate of –0.03 from the FE model (Table 1) and the observed average annual growth in real owner-occupier housing debt of around 5 per cent between 2006 and 2017 suggests that real annual consumption growth would have been around 0.15 percentage points higher had debt remained at its 2006 level (all else equal). This suggests that by 2016, consumption would have been around 1.6 per cent higher had there been no increase in debt since 2006 (Figure 7).
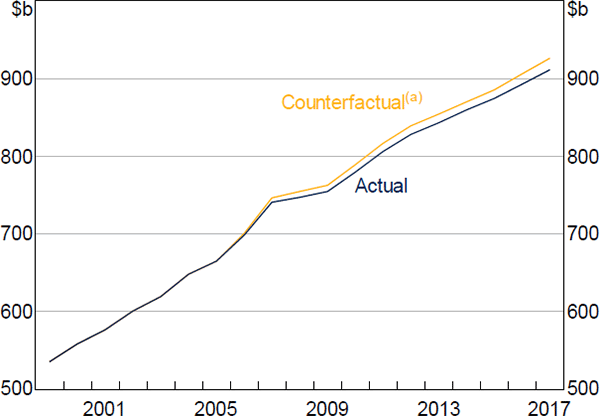
Note: (a) Assumes no change in debt between 2006 and 2017, an elasticity estimate of −0.03 and average annual growth in real owner-occupier housing debt of around 5 per cent
Sources: ABS; Authors' calculations
It is important to stress that this analysis assumes that all other economic trends that supported consumption over the period would have occurred anyway. For instance, housing prices increased strongly between 2006 and 2016, supporting consumption. But some of the increase in housing prices was likely driven by higher debt. Had debt remained at its 2006 level, house prices would not have increased by the same amount. As a consequence, the actual path of consumption includes the stimulatory effect of higher house prices through higher debt. Our estimates of a 1.6 per cent increase in consumption in the absence of an increase in debt therefore assume that housing prices would have increased for non-debt related reasons. Furthermore, we assume that all households increased their debt holdings uniformly and adjusted their spending in the same way.
7.2 Using Micro Data
To address some of the distributional concerns of differential changes in debt across households, we use the HILDA Survey data to examine how much each household changed spending due to changes in its debt holdings between 2006 and 2010, and then sum these differences across all households. In contrast to the previous section, this allows for heterogeneity in debt growth across households.[23] For each household, we compare the observed level of spending (Eh,t) with a counterfactual level of spending under the assumption that debt did not change .
The counterfactual level of spending is estimated by taking the difference between the observed spending and the attributed effect of the change in debt of each household and then summing these differences across all households. We use the level change in household debt instead of the percentage change in order to keep households in the sample without any debt in 2006 for which the percentage change would be undefined. Using the level change in debt, however, requires us to transform our elasticity estimates (the percentage spending response to a percentage change in debt) to estimates of the marginal propensity to consume (MPC, the level spending response to a level change in debt).
Using the MPC instead of elasticities is in line with the related literature on the effects of changes in wealth on consumption. We can obtain an aggregate MPC out of mortgage debt in two ways. First, we can scale our estimated elasticity coefficient by the ratio of aggregate total consumption expenditure to lagged mortgage debt. From 2006 to 2010, the ratio of annual consumption to owner-occupier mortgage debt averaged at around 105 per cent, which – multiplied with our coefficient of −0.03 from the FE model in Table 1 – implies an aggregate MPC of −3.2 cents per dollar increase in mortgage debt. Second, we can estimate the MPC directly by re-specifying our regression in level changes rather than using the IHS transformation. Our dependent variable is then the change in household spending, and our three main independent variables are level changes in income, lagged housing debt and lagged home value. The average MPC we obtain using this approach is around – 2.0 cents per dollar (not statistically significant at the 10 per cent level).[24]
Using our estimates for the MPC, we can then obtain the counterfactual level of aggregate spending as:
The results of the counterfactual exercise are presented in Table 8. Interestingly, the micro data estimates suggest that the effect of debt on aggregate spending is of similar magnitude to the effect using macro data estimates. Using the elasticity-implied MPC out of debt of −3.2 cents per dollar suggests that the changes in mortgage debt between 2006 and 2010 reduced annual aggregate total spending growth over this period by 0.36 percentage points. Using the directly estimated MPC of −2.0 cents per dollar lowers this estimate to 0.24 percentage points lower aggregate total spending growth annually.
| Aggregate total spending growth | |
|---|---|
| Elasticity-implied MPC out of debt | −0.36 |
| (−3.1 cents per dollar) | [−0.72, <0.00] |
| Estimated MPC out of debt | −0.24 |
| (−2.0 cents per dollar) | [−0.71, 0.24] |
|
Note: 95 per cent confidence intervals provided in square brackets Sources: Authors' calculations; HILDA Survey Release 17.0 |
|
Overall, both the macro data and micro data estimates imply that higher aggregate debt levels alone can have an economically significant effect on macroeconomic activity. Again, it is important to note that these estimate do not account for possible stimulatory effects of debt. Furthermore, while this exercise captures differences in changes in debt across households, we do not consider how the MPC varies across households. As discussed in Section 7.1, it is possible that there are meaningful differences in the effect of debt across households and this variation could have important implications for the aggregate effect.
Footnotes
Household survey estimates indicate that, in 2004, households spent only around 13 per cent of the equity withdrawn in the process of a property transaction on consumption items, mainly durables, and in particular motor vehicles (Schwartz et al 2006). [21]
To best understand the effect on the aggregate, one could use a structural model that explicitly allows for heterogeneous agents, financing frictions and general equilibrium effects (e.g. Kaplan, Moll and Violante 2018). We leave this for future work. [22]
It also allows us to consider the full sample of households, not only households with mortgage debt. [23]
When we control for level changes in lagged housing equity instead of lagged home value, we obtain an MPC of 2.5 cents per dollar. Our three estimates for the MPC out of mortgage debt are broadly of similar size compared to estimates for the MPC out of housing wealth for Australia of around 2.5 cents per dollar (Dvornak and Kohler 2007; Windsor, Jääskelä and Finlay 2013; Gillitzer and Wang 2015). [24]