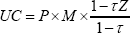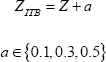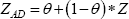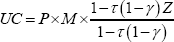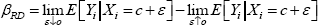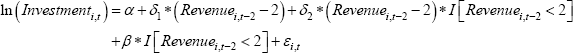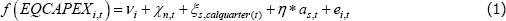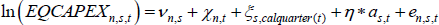Research Discussion Paper – RDP 2018-07 The GFC Investment Tax Break
1. Introduction
The effect of business taxation on investment remains a relevant question, more than 50 years after Hall and Jorgensen (1967) kick started its modern study. As was the case then, policymakers still frequently use investment tax incentives as a countercyclical tool.[1] The potential for higher investment is a key argument in current debates around lowering company tax rates.[2] The relationship between tax and investment has implications for the potency of monetary policy, as monetary policy is often considered to act through a similar intertemporal substitution channel.[3]
Most recent work indicates that tax incentives raise investment. Zwick and Mahon (2017) find that accelerated depreciation available in the United States during two periods in the 2000s raised investment in eligible capital considerably. House and Shapiro (2008) found a similar result for the earlier of the two periods. The more interesting question now is probably: what mechanisms underlie the response of investment? Zwick and Mahon found that financially constrained companies react more strongly than other companies, and that companies only respond when incentives reduce tax payable in the current year. These findings suggest that tax incentives operate at least partly through mechanisms other than lowering the cost of capital.
We study the effect of an investment tax break that was in effect in Australia during the global financial crisis (GFC). An (almost) unique feature of Australia's tax system – corporate dividend imputation – means that our work provides direct evidence on the mechanisms underlying the investment response to tax incentives.[4] Under dividend imputation, tax paid by companies becomes a credit for personal income tax for resident shareholders. This means that the (small) companies that we study faced no fall in their cost of capital from the tax break, so any measured response is being driven by other, ‘non-standard’, mechanisms. Some features of the policy itself also make it worth studying. It was around five times more generous than the US policies that were in effect during the 2000s, was available for a much shorter period, and provided the same benefit no matter the effective life of the asset. This means it provides a test of intertemporal substitution: the primary mechanism through which tax incentives operate in a standard model.
The tax break we study was part of the Australian Government's stimulus response to the global financial crisis.[5] No previous empirical work has been done assessing the effectiveness of the investment tax break, so our work is also of direct interest to Australian policymakers. Differences in taxation systems (other than dividend imputation) and economic structure mean that the response of investment to tax incentives is likely to vary across countries.
What did the tax break involve? During the first half of 2009, all businesses received an extra tax deduction of at least 30 per cent on investment in equipment, plant and machinery. For business profits taxed at a rate of 30 per cent, this is equivalent to a fall of around 12 per cent in the after-tax cost of investment, when evaluated in a standard investment model. During the second half of 2009, smaller businesses – those with revenue below $2 million – received extra deductions of 50 per cent, generating even larger falls in the after-tax cost of investment, whereas larger businesses received a benefit of 10 per cent. Australian Taxation Office data indicate that businesses claimed at least $15 billion of extra deductions under the investment tax break (ATO 2016).
We use large business-level datasets and modern policy evaluation techniques to study the effect of the tax break. The design of the tax break means that the best way to study its effect is to look at differences between small and large businesses, so a dataset separating the investment of small and large businesses is needed. Data that distinguish between investment in equipment, plant and machinery (‘equipment’ investment) and investment in building and structures (‘building’ investment) are also useful, as the tax break applied only to the former. Our datasets, tax data on the population of businesses from the Business Longitudinal Analysis Data Environment (BLADE)[6] and business-level data from the Survey of New Capital Expenditure (both provided by the Australian Bureau of Statistics (ABS)), have these features.
We apply both difference-in-differences (DD) and regression discontinuity (RD) methods to the datasets. Our DD strategy compares the investment of small and large businesses within a given industry, and, after accounting for a number of other controls, takes this difference as the effect of the tax break. This strategy controls for differing industry conditions, a key improvement on past studies. Our RD strategy refines this by using the large discrete difference in the generosity of the tax break around the $2 million revenue threshold to identify its effect.
All of our statistical work indicates that businesses responded strongly to the tax break. Moreover, we find that – despite the existence of dividend imputation in Australia – companies increased their investment significantly in response to the tax break. This indicates that the effect of tax incentives on investment operates at least partly through non-standard mechanisms. One potential such mechanism is a relaxation of financial constraints, as the tax break frees up additional cash flows by allowing the company to delay the taxation of income. To the extent that this is the case, it may suggest that such polices are more effective during downturns when financial constraints are more binding. We also find no indications of intertemporal substitution, which provides more evidence for the importance of non-standard mechanisms. Specifically, we find that businesses eligible for the highest rates of the tax break did not invest less than other businesses in the years after its expiry.
Our estimate of the aggregate tax elasticity of investment is below that provided for the United States by Zwick and Mahon (2017), consistent with the different tax treatment of companies in Australia. When we instead focus on unincorporated businesses, which are subject to a similar taxation regime to US companies, the estimates are similar to those for the United States.
On the policy front, we provide partial and general equilibrium estimates of the macroeconomic importance of the tax break. These estimates suggest that both GDP growth and the cash rate would have been significantly lower in 2009 in the absence of the tax break.
While our work suggests that tax rates and breaks can affect real decisions for Australian companies, despite the existence of the dividend imputation system, it provides only limited guidance on the potential effects of policies other than the one we study. Other policies will differ in terms of their timing, permanence and targeting, all of which could influence their effectiveness.
2. Related Theory and Literature
This section reviews the economic theory regarding the determinants of business investment and outlines how the tax break we study relates to this theory.
The modern study of the relationship between business taxation and investment began with Hall and Jorgenson (1967), who derived an expression for the cost to a company of employing fixed assets:
This user cost of capital is a key determinant of investment choices in a standard investment model. P is the real price of investment goods and M is the weighted average cost of funds (debt and equity) of the company. τ is the company tax rate. The user cost for an unincorporated business replaces τ with the average marginal tax rate of its owners. Z is the ratio of the present value of future depreciation allowances to the initial purchase price of the asset. These allowances permit businesses to deduct the cost of the capital investment from their taxable income over a multi-year period that approximates the economic life of the asset.
Given discounting of future cash flows, in normal times Z is always less than 1. For equipment in Australia, a reasonable baseline value is 0.85. The investment tax break we study involves an additive increase to Z:
The early literature (including Hall and Jorgenson) used aggregate time-series data to show that the user cost was a significant determinant of investment. This early literature is well surveyed by Hassett and Hubbard (2002). While there was some apparent success, later contributions showed that most of the apparent relationship was due to the relationship between recent economic growth and current investment: this is the standard ‘accelerator effect’ that has been known about since Clark (1917). Cockerell and Pennings (2007) provide an Australian version of this result. In their models, the cost of capital generally has a statistically significant negative coefficient, but most of the explanatory power is provided by other cyclical variables such as business confidence and the real exchange rate.
The more recent literature has focused on using changes in tax parameters to estimate the relationship between the cost of capital and investment. Such changes are more plausibly exogenous than variation in financing costs (Cummins, Hassett and Hubbard 1994), and are less prone to measurement error. This is the approach taken in the two papers cited in Section 1: Zwick and Mahon ((2017); henceforth ZM) and House and Shapiro ((2008); henceforth HS).
These papers focus on policies allowing for accelerated depreciation of equipment investment that were in force in the United States during 2001–04 and 2008–11. Accelerated depreciation differs from the investment tax break we study – it brings forward depreciation deductions to the first year of an asset's life, rather than simply increasing their aggregate nominal value. This leads to additive and multiplicative adjustments to the present value of depreciation deductions. If θ represents the share of depreciation deductions accelerated into the first year, then:
Accelerated depreciation is more valuable to businesses with longer-lived capital, for whom Z is lower. Both studies use this cross-sectional heterogeneity in the effective lives of capital, and therefore the value of accelerated depreciation, for identification.
ZM use firm-level US tax data in a continuous DD set-up, as they have data to measure ZAD accurately across industries. They find a relationship between investment and the cost of capital that is significantly stronger than that found in the early literature. Their estimates indicate that accelerated depreciation raised eligible investment by 10 per cent during 2001–04 and by 17 per cent in 2008–10, relative to ineligible investment. These are significant changes, given that accelerated depreciation increased average Z by around 5 percentage points in the first period and 7 percentage points in the second period. As noted above, the investment tax break we study raised Z by between 10 and 50 percentage points.
HS build a structural model of investment, and show that under certain assumptions, the parameters governing the relationship between tax incentives and investment can be easily estimated. The assumptions they require are that the tax incentive is sufficiently temporary, and that capital is sufficiently long-lived. Under these assumptions they show that the intertemporal elasticity for investment is essentially infinite, as businesses face very large incentives to bring forward investment in long-lived capital to periods when they face lower after-tax prices. This implies that the responsiveness of investment to changes in the cost of capital (i.e. the supply elasticity) can be estimated directly from data on investment quantities. Using industry-level data on investment quantities from the first bonus depreciation period, HS estimate a supply elasticity that – once data differences are accounted for – is similar to that estimated by ZM.
HS also provide a useful discussion of earlier work that found little effect of tax incentives on investment. Goolsbee (1998) shows that investment tax incentives in the United States have a significant effect on capital prices and concludes that the supply elasticity is low. HS point out that with a very high demand elasticity, before-tax prices adjust to reflect the full cost of any subsidies, so focusing on prices is not a robust way to estimate supply elasticities. In addition, HS do not find similar price effects to Goolsbee in their analysis. HS also point out that the DD analysis performed by Cohen and Cummins (2006) used treatment and control groups that both received quite similar benefits from the policy under examination, and that this explains why they found the policy to be ineffective.
There has been less empirical analysis of the relationship between taxes and business investment in Australia. This is despite a rich history of relevant changes in taxation, including a sharp change in the depreciation schedule in 1999 (Reinhardt and Steel 2006). La Cava (2005) uses panel data to analyse the importance of financial factors on company investment, but does not examine the effect of legislative changes to depreciation schedules. AlphaBeta (2018) is a recent example that examines changes to the company tax rate for small companies that occurred in 2015. They find that affected businesses increased investment and employment.
Australia offers an interesting prism through which to examine the interaction between tax changes and business investment, given the different tax arrangements for unincorporated businesses and companies, with the latter having access to dividend imputation. A number of papers have found that dividend imputation affects the financial choices of companies in Australia. Callen, Morling and Pleban (1992) find that dividend imputation increased dividend payouts by about 20 per cent in the five years after its introduction. Twite (2001) presents evidence that businesses adjusted their capital structure away from debt after the introduction of dividend imputation.
Officer (1994) provided a user cost of capital formula applicable to a company under dividend imputation:
The difference in the user cost equations is γ ∈[0,1], which measures the value of a dollar of tax paid at the company level to a shareholder. This value reflects the fact that, under dividend imputation, tax paid at the company level is a credit for personal income tax for resident shareholders. If the value of γ is 1, indicating that the tax paid at the company level lowers shareholders' tax dollar-for-dollar, then company taxation does not appear in the user cost formula. Moreover, Z does not affect the cost of capital in this situation.
The evidence on the value of γ in Australia is mixed. Many large Australian companies raise equity from international investors, who derive no benefit from dividend imputation. As such, γ is unlikely to be 1 for these businesses. Applied evidence based on samples of listed companies finds a range of values for γ (Swan 2018). Our analysis focuses on smaller companies, who have very few non-resident shareholders. A company owned entirely by residents should have a value of γ close to 1 (this is discussed further below).
3. Background on the Tax Break
In this section we make the theory outlined in Section 2 more concrete by providing further detail on the tax break and Australia's business taxation rules.
For equipment investment committed to between 13 December 2008 and the end of 2009, businesses could make an extra, immediate, tax deduction equal to a proportion of the value of the asset. This extra tax deduction did not affect the standard tax depreciation deductions for the asset, so allowed businesses to make deductions exceeding 100 per cent of the value of an asset over its life. The extra tax deduction was immediate in the sense that it could be deducted in the current tax year. The official title of the investment tax break was the ‘Small Business and General Business Tax Break’. Notably, the tax break applied only to equipment investment, and provided no benefit for building investment.[7]
When the policy was first announced in December 2008, the tax break afforded all businesses an extra deduction of 10 per cent (Swan 2008). Subsequent government announcements over the first half of 2009 made the tax break more generous, until it reached its final form in mid May 2009 (Swan 2009a, 2009b). The final form included differentiated deductions for small and large businesses, with small businesses afforded a 50 per cent deduction, and large businesses being afforded a 30 per cent deduction for investments committed to before 30 June 2009 and a 10 per cent deduction for those committed to during the second half of 2009.
The time-series profile of bonus deductions is shown in Figure 1. While the final rates announced in May 2009 applied retroactively to earlier investment, it is the rates that businesses thought to be applicable in each period that would have governed their behaviour, and so we focus on the rates as announced.
The legal definition of a small business, and thus eligibility for the higher rate of tax break, is complicated. Under the relevant law, a business qualifies if any of these conditions are satisfied:
- revenue in the previous financial year was less than $2 million;
- revenue in the current year is likely to be less than $2 million (as judged at the start of the year), provided revenue in at least one of the two previous years was less than $2 million; or
- revenue in the current year is less than $2 million (measured at the end of the current year).[8]
Businesses that do not meet any of these criteria are considered to be large businesses and are therefore only eligible for the lower rates of bonus deductions.
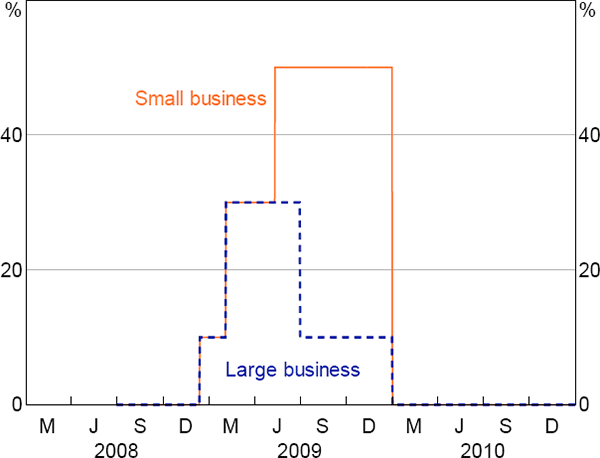
Sources: Swan (2008, 2009a, 2009b)
Table 1 presents hypothetical tax deductions for a $100,000 piece of equipment capital under normal rules and varying rates of tax break. Under the normal depreciation rules, a business is allowed to deduct 20 per cent of the value of its investment, or $20,000, in each year of the effective life of the item. Assuming the marginal tax rate of the business is constant at 30 per cent, this equates to a reduction in tax payable of $6,000 per year. Using a reasonable discount rate, the present value of these deductions is around $88,000, or 0.88 of the purchase price (this is Z). The present value of tax benefits is around $26,000, or 0.26 of the purchase price (this is τZ).
The tax break changed this sequence of deductions and tax benefits only in the first year. With an extra deduction equivalent to 10 per cent of the value of the item, a business can make a $30,000 deduction in the first year, which translates to a tax benefit of $9,000. With 50 per cent bonus depreciation, the tax benefit in the first year is $21,000, $15,000 higher than under normal depreciation. The tax break increases Z from 0.88 under normal rules to 0.98 with a 10 per cent deduction, and to 1.38 with a 50 per cent deduction.
How do these tax benefits flow through to the owners of businesses with different legal types? For owners of unincorporated businesses, the tax benefits are exactly as shown in Table 1, with 30 per cent replaced by the relevant marginal tax rate of the owner(s). Table 2 outlines the benefits of the investment tax break for a company owned (solely) by a resident shareholder and a company owned (solely) by a non-resident shareholder. The hypothetical company makes $200,000 in net profit and receives an extra $20,000 deduction from the tax break. The key point is that the resident shareholder receives no increase in after-tax income, while the non-resident shareholder receives a benefit.
| Years ($'000) | Present value | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | $'000 | Share of purchase price | ||
| Normal depreciation | ||||||||
| Deduction | 20 | 20 | 20 | 20 | 20 | 87.7 | 0.88 | |
| Tax benefit (at 30 per cent marginal tax rate) | 6 | 6 | 6 | 6 | 6 | 26.3 | 0.26 | |
| With 10 per cent bonus deduction | ||||||||
| Deduction | 30 | 20 | 20 | 20 | 20 | 97.7 | 0.98 | |
| Tax benefit (at 30 per cent marginal tax rate) | 9 | 6 | 6 | 6 | 6 | 29.3 | 0.29 | |
| With 50 per cent bonus deduction | ||||||||
| Deduction | 70 | 20 | 20 | 20 | 20 | 137.7 | 1.38 | |
| Tax benefit (at 30 per cent marginal tax rate) | 21 | 6 | 6 | 6 | 6 | 41.3 | 0.41 | |
| Notes: 7 per cent discount rate used for present value; example constructed using the prime cost method | ||||||||
| Australian resident (γ = 1) | Non-resident (γ = 0) | ||||
|---|---|---|---|---|---|
| Without tax break | With tax break | Without tax break | With tax break | ||
| Company level | |||||
| Profit before depreciation | 200 | 200 | 200 | 200 | |
| Investment tax break deductions | 0 | 20 | 0 | 20 | |
| Taxable profit | 200 | 180 | 200 | 180 | |
| Company tax (30 per cent flat rate) | 60 | 54 | 60 | 54 | |
| Dividend paid | 140 | 146 | 140 | 146 | |
| Franking credits distributed | 60 | 54 | 60 | 54 | |
| Shareholder level | |||||
| Assessable income (in resident country)(a) | 200 | 200 | 140 | 146 | |
| Income tax (30 per cent flat rate)(b) | 60 | 60 | 42 | 44 | |
| Value of imputation credit received | 60 | 54 | 0 | 0 | |
| Net tax payable | 0 | 6 | 42 | 44 | |
| After-tax income | 140 | 140 | 98 | 103 | |
|
Notes: (a) Dividends plus franking credits for resident; for non-residents, we abstract from Australian withholding taxes and associated foreign income tax credits |
|||||
This example shows how different assumptions about the residency of shareholders, and therefore about the value of γ, can lead to very different conclusions about the effect of the tax breaks on companies' costs of capital. The common assumption in computable general equilibrium models, which are often used in modelling the effects of tax changes on macroeconomic outcomes, is that Australia is a price-taker in capital markets. This means that the cost of capital is set by foreign investors who receive no benefit from the imputation credits. That is, γ is effectively equal to zero. Examples of this approach include Dixon and Nassios (2016) and Kouparitsas, Prihardini and Beames (2016).
This assumption makes sense in the context of these papers, though it does contrast with recent empirical evidence from Swan (2018). It requires perfect international capital mobility, which might be the case over the long horizons examined in these papers. Moreover, much of the investment undertaken in Australia is done by large listed companies, who frequently have a significant proportion of non-resident shareholders, and so assuming γ is equal to zero might be reasonable when trying to model aggregate macroeconomic outcomes.
For our purposes, however, the assumption that γ is equal to zero is unlikely to be appropriate. We study small companies with revenue around the $2 million threshold. Tax data indicate that these companies are almost exclusively owned by Australian residents, who get full value from the imputation credits. It is unlikely that capital markets are so complete that the cost of capital for these companies is wholly determined by non-resident investors. This is particularly true over the short horizon we consider. For these reasons, we think that it is reasonable to assume that the value of γ in the user cost equation is close to 1 for our sample.
In this case, there will be no change in the user cost of capital for companies as a result of the tax break. For this reason, we interpret any significant response from companies as evidence that the investment tax breaks operate through other, non-standard, mechanisms. As a corollary, we also expect companies to respond less strongly to the tax incentives than (similar) unincorporated businesses, who benefit both from a lower cost of capital and these non-standard mechanisms.
The key non-standard mechanism that we suggest is financial constraints on companies' investment decisions, which may be particularly relevant for the small companies we consider. Such constraints may include very high costs of external finance, or the inability to access such finance. As a concrete example, the extra cash available as a result of the tax break could make a range of investments feasible by lowering the amount of external finance required. The same story could be told for companies relying entirely on internal finance: the extra cash available could make it possible to finance some additional investment using their own internal resources.
4. Data and Methodology
This section explains the two different methodologies and two different datasets that we use to measure the effect of the tax break.
4.1 RD with BLADE
The definition of a small business lends itself to RD methods. This is because whether or not a business is small (the treatment), and therefore the level of the tax break, depends on whether a continuous ‘forcing’ variable (revenue in past years) is above or below a threshold ($2 million). Our RD set-up looks at investment for businesses with revenue just above the threshold, and those with revenue just below the threshold, and takes the difference to be the effect of the treatment. The underlying assumption is that businesses just either side of the cut-off will be nearly identical along all relevant dimensions, except for the size of the tax break. Under certain assumptions – including that the businesses cannot manipulate revenue and so self-select into treatment – treatment is as good as randomly assigned and the approach is equivalent to a randomised experiment.[9] This is the approach we take in Section 5.
Establishing a clean regression discontinuity requires us to focus on a subset of businesses. For the RD analysis, we focus on 2009/10, which we refer to as time t. This is the year in which the difference in the tax break for small and large businesses was at its largest.[10] We further limit the dataset to businesses with revenue above $2 million in 2008/09 (t − 1). Based on the tax rules, these businesses could qualify as small businesses only if:
- their revenue in 2009/10 (measured at the end of the year) was below $2 million; or
- they had revenue below $2 million in 2007/08 (t − 2) and they expected revenue in 2009/10 to be below $2 million.
As condition (a) provides a possible way to manipulate treatment, we drop any businesses with revenue in 2009/10 below $2 million from the sample. Condition (b) then provides an appropriate forcing variable for our subset of businesses: revenue in 2007/08. The remaining businesses in the sample were large if their revenue in 2007/08 was above $2 million. Otherwise, they were small businesses, provided they could reasonably expect their revenue in 2009/10 to be less than $2 million.
To deal with this expectational requirement, we further exclude businesses in 2008/09 with revenue above a ceiling. We do so because revenue in the previous year is one of the most relevant considerations when projecting current year revenue (ATO 2017b), and so businesses with revenue above a ceiling in the previous year would be unlikely to be able to argue that they are small. Setting the ceiling too high would mean that we treat some large businesses as small businesses and, under the maintained hypothesis, this would bias our estimates down. Setting the ceiling too low would mean that we are throwing away useful observations and would lead to a loss of efficiency. We choose a ceiling of $2.5 million. While somewhat arbitrary, the results are robust to the choice of ceiling (see Appendix B).
Figure 2 provides a visual representation of this selection rule. We are left with businesses with: revenue in 2008/09 between $2 million and $2.5 million; and revenue in 2009/10 above $2 million. We then focus on a subset of businesses with revenue in 2007/08 within an interval around the $2 million threshold (we discuss the selection of this ‘bandwidth’ in Section 5.1).
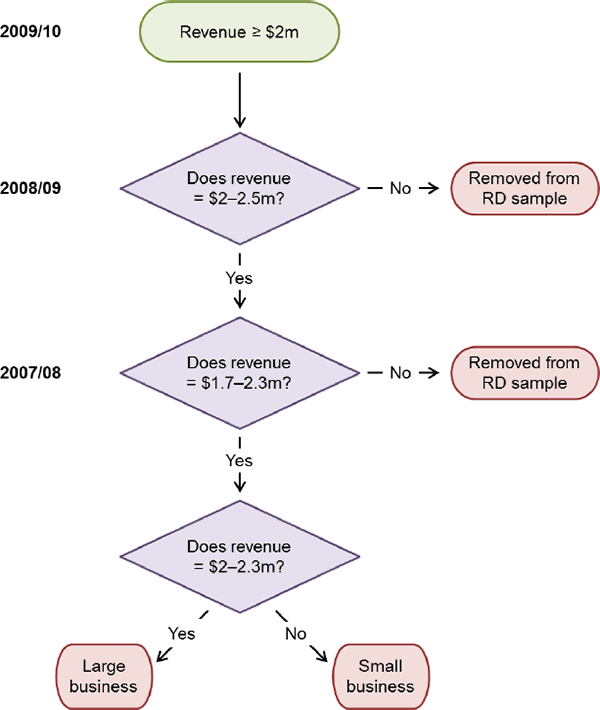
We apply RD methods to a dataset derived from the ABS's BLADE (Hansell and Rafi 2018). This dataset contains administrative tax data for almost the entire population of Australian companies and unincorporated businesses.[11] The size of this dataset makes it ideally suited to the RD approach, which requires enough observations close to the threshold to form an estimate of the effect (once we have applied the trimming discussed above).
Our RD results with the BLADE data provide our most robust estimate of the causal effect of the investment tax break upon investment. But some elements of this approach are unsatisfactory. First, the BLADE data only contains data on aggregate building and equipment investment, while the tax break applied only to the latter.[12] This means that we are estimating the response of total investment to an equipment investment tax break when using BLADE. Second, despite its large size, once we narrow the BLADE sample sufficiently to run our RD model there almost no unincorporated businesses left. As such, the approach provides estimates for companies only and does not allow us to check for heterogeneous responses across business types. Finally, the treatment effect estimated using RD is very local, as it only tells us about the effect of the treatment for businesses with revenue close to the threshold, and even then only businesses that have a revenue path that meets our trimming rules (i.e. that grow somewhat year-to-year). The response to the tax break for these businesses might differ from that of businesses of different sizes and growth paths.
4.2 DD with Capex Survey Data
Our second dataset – business-level data from the ABS's Survey of New Capital Expenditure (Capex Survey) – allows us to address some the weaknesses of the RD analysis. This survey seeks responses from around 9,000 businesses each quarter, and is used to estimate quarterly population-level capital expenditure (capex) aggregates for Australia. It separates equipment and building investment, which allows us to concentrate on equipment investment, and to run a placebo test using (ineligible) building investment. An additional advantage is that we can work with population-level data by applying sampling weights. This approach allows us to easily estimate an aggregate response to the tax break, and evaluate its macroeconomic importance.
The dataset has two key drawbacks. First, the Capex Survey dataset does not allow us to measure past revenue as precisely as in BLADE due to sample rotation. As such, we take the simple approach of designating businesses with revenue below $2 million in the financial year prior to the current quarter as small, and all other businesses as large. This is an approximation of the detailed eligibility rules discussed above. The second key drawback of this dataset is that we cannot use RD methods – it does not have sufficient observations in the vicinity of the threshold.
Instead we apply a DD model to the Capex Survey data. This approach relies on identifying a control group (large businesses) and a treatment group (small businesses). It measures the effect of the tax break as the difference between the change in investment for the treatment group across the treatment and non-treatment periods, and the change for the control group across the two periods. The key assumption underlying this approach is that in the absence of treatment, the control group and the treatment group would have behaved similarly (the parallel trends assumption).
The causal identification in the DD model is likely to be weaker than in the RD model. This is because the parallel trends assumption is a much stronger assumption than that used in RD. Still, we present evidence below that the parallel trends assumption is satisfied, particularly for our preferred control group of businesses with lagged revenue between $2 million and $10 million.
Moreover, because of the less data-intensive nature of DD, it allows us to examine heterogeneity across business types and sizes.[13]
5. RD with BLADE
Before outlining the formal model, we provide a graphical version of the RD analysis. Figure 3 plots log investment against revenue in 2007/08. The dots represent the mean investment by businesses falling into different revenue buckets ($20,000 wide). The red and blue lines are lines of best fit, estimated separately for businesses above and below the $2 million threshold using a linear (OLS) model and a local quadratic polynomial, respectively. All three provide evidence of a sizeable fall in investment at the threshold, indicating that the tax break affected investment. This is even clearer if we plot the residuals from a regression of investment on industry dummies, instead of investment itself, which accounts for the fact that businesses in certain industries are likely to invest more heavily (Figure 4).
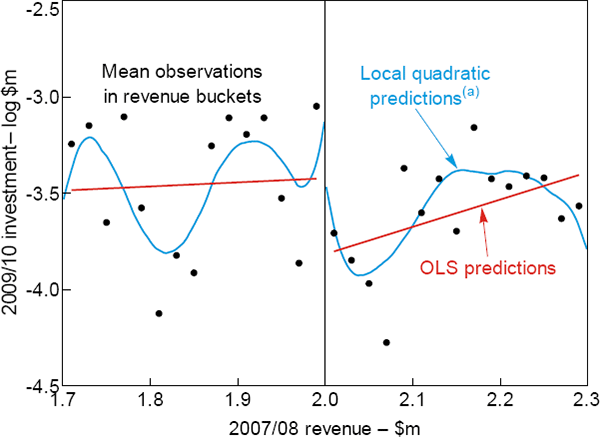
Note: (a) Modelled using Epanechikov kernel with a bandwidth of 0.05
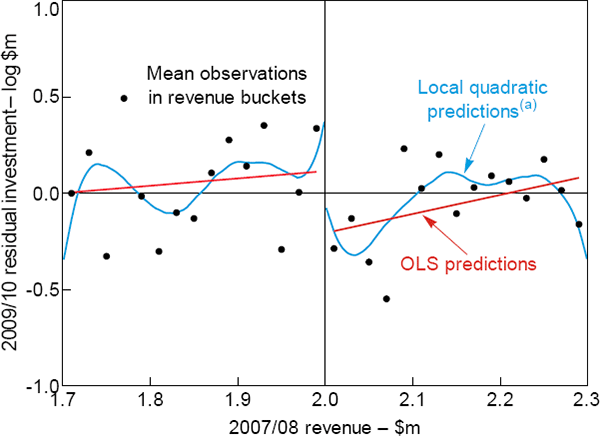
Notes:
Residual investment is from regression of log investment in 2009/10 on industry fixed effects
(a) Modelled using Epanechikov kernel with a bandwidth of 0.05
5.1 Econometric Methodology
In an RD model, the estimate of the effect of the treatment, β, is taken as the difference between the conditional mean just below the threshold and the conditional mean just above the threshold. That is:
where βRD is the regression discontinuity estimate, Yi is the variable of interest, Xi is the forcing variable and c is the threshold.
The problem can be thought of as estimating a local polynominal model on either side of the threshold to estimate the conditional means. This leads to three modelling choices:
- Bandwidth: This determines whether observations a long way away from the point of interest are included in the regression. A high bandwidth means we include observations a long way away from the threshold, whereas a low bandwidth means we focus only on near observations. Bandwidth choice amounts to weighing up bias, which increases with the bandwidth as we are including observations far away from the point of interest, with efficiency, which rises with the bandwidth as we are including more observations and getting more information. We choose a bandwidth of $270,000 based on the mean squared error minimising plug-in estimator of Imbens and Kalyanaraman (2012).
- Kernel choice: The choice of kernel determines the weights different observations are given in the polynomial regression. We use a rectangular or uniform kernel, which gives equal weight to all observations and amounts to only including observations within the bandwidth (i.e. revenue in 2007/08 between $1.73 million and $2 million for the conditional mean below the threshold, and between $2 million and $2.27 million for the conditional mean above).
- Polynomial order: This is the order of the polynomial in the forcing variable that is used to fit the data. A higher-order polynomial will more flexibly fit the data, especially if we have to use a high bandwidth due to a lack of observations around the threshold. However, increasing the order of the polynomial could lead to overfitting. We focus on a polynomial of order 1 (i.e. a linear model). We use the test suggested by Lee and Lemieux (2010) and find this is sufficient for our baseline bandwidth.[14]
Appendix B provides robustness testing around these modelling choices.
Given these modelling choices, our RD model is:
where the business identifier is i, t is the year 2009/10, and I is an indicator variable that takes on the value 1 if the condition in the brackets is met. The coefficient of interest, β, captures the discontinuity at the revenue threshold. A significant and positive estimate for this coefficient would indicate that the higher tax break led small businesses to invest more.
As we model the log of investment, any observation of zero investment is discarded. This accounts for a non-negligible portion of the sample. As such, the estimates are estimates of the effect of the tax break on businesses' investment at the intensive margin (i.e. how much they invest, conditional on investing). We use the log of investment, instead of levels, as this enables us to compare our estimates to the semi-elasticities reported in the existing literature.
5.2 Baseline Results
Table 3 shows the results from this baseline model.[15] Model 1 is the model outlined in the previous subsection. Models 2 and 3 incorporate some additional covariates, namely revenue in period t and t − 1, and ANZSIC division dummies.[16] While the RD approach does not require the inclusion of covariates, doing so can increase the efficiency of the estimates and help to eliminate small sample biases (Imbens and Lemieux 2008). Finally, Models 4 and 5 present the results from estimating the model using a polynomial of order 2 (i.e. a quadratic) in Revenuei,t − 2. Calonico, Cattaneo and Titiunik (2014) suggest that this is a simple way to account for asymptotic bias introduced by standard bandwidth selection methods, which tend to be too ‘large’ in asymptotic terms.[17]
| Model | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| β | 0.49** (0.19) |
0.50*** (0.19) |
0.49*** (0.19) |
0.71** (0.28) |
0.77*** (0.28) |
| Controls | |||||
| δ1 | 2.36*** (0.80) |
2.22*** (0.80) |
2.41*** (0.78) |
3.40 (1.16) |
4.64 (3.22) |
| δ2 | −1.94 (1.32) |
−1.46 (1.33) |
−1.76 (1.31) |
1.16 (4.94) |
0.35 (4.85) |
| Revenuei,t | na | 0.29** (0.14) |
0.33** (0.16) |
na | 0.34** (0.17) |
| Revenuei,t − 1 | na | 0.26 (0.42) |
0.16 (0.42) |
na | 0.13 (0.43) |
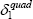 |
na | na | na | −3.81 (11.42) |
−8.18 (11.32) |
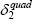 |
na | na | na | 19.89 (18.02) |
25.11 (17.64) |
| Dummies | None | None | Division | Division | Division |
| Bandwidth ($m) | 0.27 | 0.27 | 0.27 | 0.27 | 0.27 |
| Kernel | Uniform | Uniform | Uniform | Uniform | Uniform |
| Observations | 1,245 | 1,228 | 1,228 | 1,245 | 1,228 |
|
Notes: ***,**,* represent statistical significance at the 10, 5 and 1 per cent significance levels, respectively; standard errors are in parentheses |
|||||
The estimated treatment effect, β, is positive and significant in all models. Most of the estimates are around 0.5, indicating that qualifying for the higher rates of tax break available to small businesses caused businesses to invest around 65 per cent more. Using the average difference in tax break rates over 2009/10 of 20 percentage points, this translates into a semi-elasticity of investment with respect to the tax break rate of 3.25 (i.e. a 10 percentage point increase in the tax break raises investment by about 33 per cent). Given the expiry of the credit was known in advance, meaning that businesses may have brought their investment forward to the first half of the year, it is also reasonable to treat the average difference for the full year as that prevailing over the first half of 2009/10: this would give a semi-elasticity of 1.63.
Given our assumption that the tax break does not affect the user cost of capital for companies in our sample, we interpret this strong response as indicating that the tax break influences company investment through some other mechanisms. As discussed above, one potential mechanism is the relaxation of financial constraints.
The fact that we find evidence of a role for other mechanisms is consistent with ZM's finding that businesses in their sample respond more strongly when they are tax profitable, such that investment deductions reduce their current year tax, or when they are more financially constrained.
Still, these estimated elasticities are somewhat smaller than those from ZM. ZM provide a baseline semi-elasticity for their sample of 3.7, but this is estimated using a sample of companies that are mostly much larger than our RD sample (median revenue in their dataset is $26 million). Their estimate for the bottom three deciles of their sample, which are more comparable in size to our sample, is 6.3. The fact that companies in the United States respond more strongly to tax breaks than Australian companies is consistent with the difference in taxation arrangements. The United States has a classical company taxation regime whereby company dividends are subject to individual income taxes, so company tax deductions are valuable to shareholders.[18] The fact that we use total capital expenditure instead of equipment expenditure could also help to explain why our estimated coefficients are below those for the United States, as the additional noise would introduce a downwards bias. However, given we focus on small businesses that are unlikely to frequently engage in building investment, we think this bias will be very small.
The RD approach also allows us to test whether the increased investment in response to the tax break was merely brought forward from future years, or whether it represented an actual increase in the total amount of investment, and therefore the capital stock. In the former case, we would expect lower investment from small businesses in later years to make up for the higher investment in 2009/10.
We can test for this by replacing the left-hand side variable with investment in 2010/11, or in 2011/12, or the sum of the two. The results from doing so, using the specification from Model 2, are contained in Table 4. There is no evidence of lower future investment for small businesses, indicating that the investment tax break generated genuine additional investment, rather than simply bringing forward investment. This is consistent with the findings in HS and ZM. The results are robust to the choice of controls, and to re-selecting the optimal bandwidth.
| Investment for year | |||
|---|---|---|---|
| 2010/11 | 2011/12 | 2010/11–2011/12 | |
| β | 0.21 (0.22) |
0.15 (0.21) |
0.12 (0.40) |
| Dummies | None | None | None |
| Bandwidth ($m) | 0.27 | 0.27 | 0.27 |
| Kernel | Uniform | Uniform | Uniform |
| Observations | 1,150 | 1,088 | 903 |
|
Notes: Uses Model 2 from above; standard errors are in parentheses |
|||
5.3 Validity Testing
5.3.1 Placebo tests
The above results indicate that qualifying for small business status led these businesses to invest significantly more in 2009/10. One concern is that this may be unrelated to the tax break itself. There are, for example, a number of other tax concessions that were available to small businesses at the time that could have caused businesses to invest more if they were considered small for tax purposes. These include reduced taxation of capital gains, accelerated depreciation for assets worth less than $1,000, income and sales tax concessions for businesses with revenue below $75,000, and reductions in intra-year tax instalments. A table detailing these policies is provided in Appendix D.
Most of these concessions were in place prior to the financial crisis or remained in place after 2009/10. As such, if they are substantially affecting our results in 2009/10, their effect should also be evident during other years. In contrast, the effect of the tax break should only be evident in 2009/10, and possibly in 2008/09 given the tax break rate differed for the final month and a half of this year. This suggests the natural placebo test of re-running our RD model using data for other years.
We perform the placebo testing using Model 2 from above, but the results are robust to other choices. Figure 5 plots the estimated treatment effects and confidence bounds. For all years with no tax break, the treatment effect is not statistically significantly different from zero. For 2008/09, the treatment effect is significant and is estimated to be around half the size of that in 2009/10. The fact that we find a significant effect despite the relatively short portion of 2008/09 during which the tax break rates differed suggests that firms placed a high value on receiving the tax benefit immediately, rather than waiting to receive the benefit at the end of the next tax year.
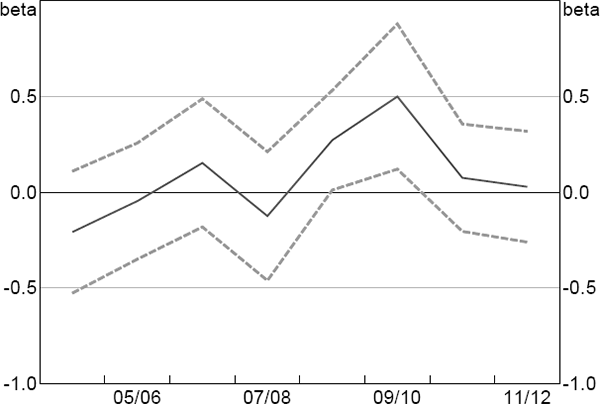
Notes: Estimated using Model 2; dashed lines are 95 per cent confidence intervals
Placebo tests can also be used to test for confounding factors that were only present during 2009/10. For example, while we are not aware of any relevant tax rules that differed by size and applied only in the years we investigate, such differences may have escaped our notice. The appropriate tests examine whether other observables that are less likely to be affected by the treatment are continuous in the forcing variable. We examine both revenue in 2009/10 and full-time equivalent employment. Using a specification based on Model 1, we find no evidence of a discontinuity.[19]
5.3.2 Manipulation tests
One of the requirements for valid RD is that businesses cannot manipulate the forcing variable, Revenue, to change their treatment status. If businesses could self-select in this way, the assumption that businesses just above and below the cut-off are identical would be violated. Businesses with a higher ex ante propensity to invest would have a greater incentive to select into treatment. In our case, manipulation of the forcing variable – revenue measured about a year before the announcement of the differential tax break – is improbable. Consistent with this, there is no graphical evidence of bunching of businesses just below $2 million of revenue in 2007/08, which we would expect to see if businesses were lowering revenue to get under the threshold (Figure 6). Applying the formal test suggested by Cattaneo, Jansson and Ma (2017) confirms this finding.
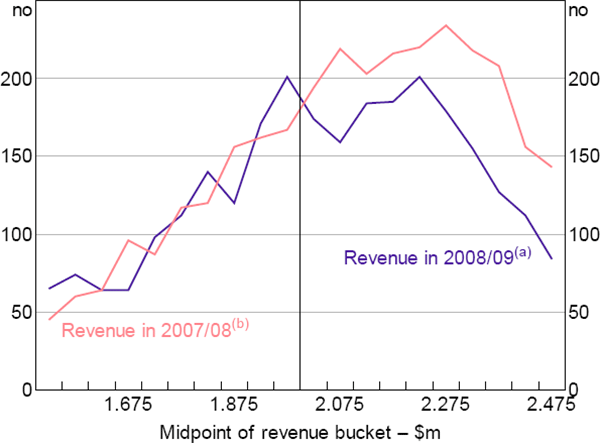
Notes:
Buckets are $50,000 wide
(a) Businesses with revenue in 2007/08 between $1.73–2.27 million
(b) Businesses with revenue in 2008/09 between $2–2.5 million and revenue in 2009/10 above $2 million
One additional concern that is fairly unique to our RD set-up is that businesses might be manipulating their way out of the estimation sample. In particular, businesses with revenue above $2 million in 2007/08, and who forecast revenue just above $2 million in 2008/09 or 2009/10, might have the incentive to manipulate their revenue in those years to qualify for the tax breaks. Based on our inclusion criteria, these businesses will drop out of our estimation sample. Moreover, businesses with a higher propensity to invest would have a greater incentive to manipulate their revenue. This would cause our sample of large businesses to have a lower propensity to investment, compared to the ‘true’ population.
There is some evidence of businesses manipulating revenue in 2008/09 to get below the threshold, with a spike in the number of businesses with revenue just below the threshold. This provides further evidence that the tax breaks were valuable to companies, as otherwise there would be no reason to manipulate their revenue. But it does suggest that there may be some threat to the validity of our identification strategy, even if the number of businesses that appear to manipulate is small relative to the total sample size.
One way to test whether our samples of small and large businesses are different is to test whether pre-determined covariates are continuous in the forcing variable. If businesses either side of the threshold really are identical apart from the treatment, their pre-determined covariates should also be identical. We test this using investment in 2007/08, before the introduction of the investment tax break, and find no evidence of a discontinuity. In the parlance of the RD literature, the density of investment in 2007/08 appears to be continuous at the threshold. This suggests the two samples do not have differing propensities to invest and supports the validity of the RD approach.
Still, even if businesses either side of the threshold had similar propensities to invest in 2007/08, it does not mean that this would necessarily be the case in 2009/10. To account for this, we rely on the fact that businesses are only likely to be able to manipulate their revenue to a certain extent. Businesses with revenue just above $2 million will likely be able to manipulate their revenue down, but businesses with revenue well above $2 million could not. As such, manipulation out of the sample, and therefore a potentially downwardly biased propensity to invest, should only be an issue for large businesses with revenue in 2008/09 and 2009/10 just above $2 million.
Table 5 contains the results from removing businesses with revenue between $2 million and $2.1 million in 2008/09 and 2009/10 from the sample. While somewhat arbitrary, the choice of a $100,000 ‘buffer’ range is supported by Figure 6. Models 6 and 7 show the results using the same bandwidth as in our baseline model, while Models 8 and 9 show the results using the automatic bandwidth selection and bias adjustment of Calonico et al (2014).
| Model | ||||
|---|---|---|---|---|
| 6 | 7 | 8 | 9 | |
| β | 0.53** (0.24) |
0.57** (0.24) |
0.45** (0.23) |
0.54** (0.23) |
| Controls | None | Revenue | None | Revenue |
| Bandwidth ($m) | 0.27 | 0.27 | 0.38 | 0.36 |
| Kernel | Uniform | Uniform | Triangular | Triangular |
| Observations | 899 | 885 | 2,371 | 2,317 |
|
Notes: Sample excludes businesses with revenue in 2008/09 or 2009/10 between $2 million and $2.1 million; ***,**,* represent statistical significance at the 10, 5 and 1 per cent significance levels, respectively; standard errors are in parentheses |
||||
Using the same bandwidth, the estimated treatment effects are broadly the same as in the baseline specification, though the point estimates are slightly higher. However, once we re-select the bandwidth, we get point estimates that are slightly below our baseline estimates. Nevertheless, the difference in the estimates is small and not statistically significant, suggesting that the fact that businesses are manipulating out of our sample is not substantially biasing our baseline estimates.
6. DD with Capex Survey Data
As discussed above, the DD approach examines differences in the behaviour of the treatment and control groups, in the treatment and non-treatment periods. In our analysis, we take businesses with revenue below $2 million in the previous financial year to be our treatment group, and other businesses to be our control group.
Again, we start by providing a graphical analysis. Figure 7 presents total equipment capex in Australia, disaggregated by revenue of the responsible business for the previous year. These data show a very clear distinction between the businesses eligible for the highest tax break rate and larger businesses during the period that the differential tax break was in effect. Equipment capex by businesses with revenue below $2 million was 58 per cent higher in 2009 than in 2008, and 40 per cent higher in 2009 than in 2010. In contrast, equipment capex by businesses with revenue between $2 million and $10 million, who were not eligible for the 50 per cent bonus rate, was only 28 per cent higher in 2009 than in 2008, and was about the same in 2009 as in 2010. Further graphical analysis of the tax break using aggregate data is provided in Rodgers (2017).
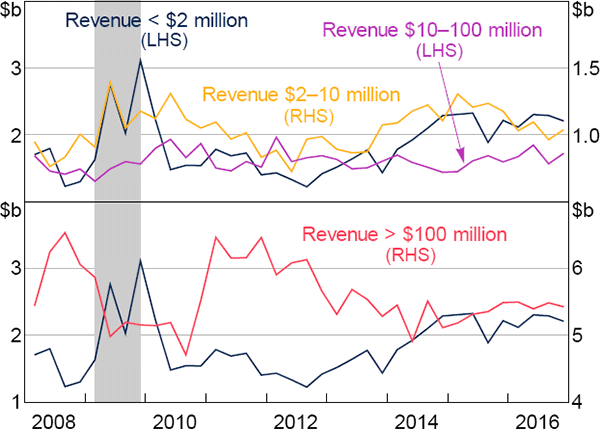
Note: Employing businesses in non-mining divisions
Source: ABS
These data also indicate reasonably parallel trends between the treatment and control groups in the non-treatment periods (2008 and 2010 onwards). Small business investment began to rise from 2013 onwards, which coincides with a number of other tax changes introduced for these businesses.
6.1 Econometric Methodology
We estimate a DD model using business-level data. We model the extensive margin (i.e. whether they invest) and the intensive margin (i.e. how much they invest, conditional on investing) separately, as in ZM. Most small businesses do not invest in a given quarter, so this approach allows us to use all of the data.
The generic specification for the models is given below. For the intensive margin model, the dependent variable (f(EQCAPEXi,t)) is the natural log of equipment capex (zero observations are excluded). For the extensive margin model, the dependent variable is the log-odds of EQCAPEXi,t > 0, calculated at the division-turnover category level, as in ZM.[20] Aggregating the extensive margin dependant variable in this way allows us to include fixed effects without losing data on businesses that invest in every quarter (or no quarters).
In the specification, i denotes a business, s denotes the revenue size categories (< $2 million, $2–10 million, $10–100 million, and > $100 million), n denotes ANZSIC divisions, and t denotes time (which is quarterly in this dataset). The explanatory variables are:
- Business fixed effects (νi): these control for characteristics of each business that drive investment but do not vary over time.
- Industry-quarter dummy variables (Χn,t): These control for differing conditions across industries during our sample period. In particular, they control for different industry experiences during the GFC.
- Seasonal dummy variables by size bucket (ξs,calquarter(t)): These control for differing seasonal patterns across businesses of different size.
- The level of the investment tax break (as,t): This is our treatment variable, and we parameterise it with the data shown in Figure 1.[21] Treatment intensity differs between small and large businesses in the final three quarters of the 2009 calendar year. These differences allow us to estimate η, the semi-elasticity of investment with respect to the tax break.
We estimate this model using data from the first quarter of 2008, as we cannot measure the business size for earlier capex observations. We stop the estimation in the middle of 2012 to abstract from the effect of other investment tax breaks for small businesses.[22]
Businesses in the revenue categories above $2 million – who received lower levels of the investment tax break – are the control group in this DD set-up. Our basic identification assumption is that differences in equipment capex between businesses with revenue below $2 million and this control group are entirely due to the investment tax break. To be more nuanced, this comparison is done after accounting for the average difference in equipment capex between small and large businesses within each industry across time. Or to put it another way, we are comparing investment for small and large businesses within each industry.
We use the $2 million to $10 million revenue size category as our baseline control group, but we also present results using a broader control group. Our motivation for concentrating on the narrower control group is that the parallel trends assumption required for identification seems more reasonable for small and medium businesses, than for small and large businesses. It seems more likely that conditions during the crisis would have affected investment by small and medium businesses similarly, compared with small and large businesses. A further issue is that ZM found that larger businesses have a weaker response to tax breaks. Heterogeneity of this type will bias our estimate of η upwards.
6.2 Baseline Results
Table 6 contains the baseline results from the intensive margin DD model for the Capex Survey dataset. When the control group is businesses with revenue in the $2–10 million range, the estimated semi-elasticity is around 1, and is statistically significant at the 1 per cent level. This translates into a 10 per cent increase in equipment capex in response to a 10 percentage point increase in the investment tax break, and an elasticity of investment with respect to the cost of capital of 2.5. When the control group is all businesses with revenue above $2 million, the estimated semi-elasticity is bit larger.
| Control group | ||
|---|---|---|
| $2–10 million | > $2 million | |
| η | 0.98*** (0.30) |
1.40*** (0.18) |
| Clusters (businesses) | 5,724 | 11,019 |
| Business fixed effects | Yes | Yes |
| Observations | 14,379 | 58,856 |
|
Notes: *** indicates significance at the 1 per cent level; standard errors are in parentheses and are clustered at the business level |
||
This baseline semi-elasticity from the DD model is slightly below the range estimated using the RD model. We think the most likely reason for this is that the estimate from the RD model is very local and is potentially only valid for the small range of businesses used in the estimation. The estimate from the DD model applies to a broader range of businesses, though the causal identification is less robust. In this sense, they are both ‘true’ estimates of the effect, but for different samples of businesses.
There are also some factors that could potentially be biasing our estimates from the DD model towards zero:
- The rule used to determine whether businesses are small when using the Capex Survey data could misclassify some small businesses as large. Some businesses might have been able to qualify as small based on having revenue below $2 million two years ago. If there are a large number of such businesses, under our maintained hypothesis this would bias our results down. The spike in investment by businesses in the $2–10 million bracket in June quarter 2009 would be consistent with this story. Businesses with revenue below $2 million in 2006/07, above in 2007/08, and that also met the expectational requirement, would have a strong incentive to take advantage of larger deductions before they start being considered large businesses for tax purposes in 2009/10.
- There may be timing differences between when investment is undertaken for tax purposes, and when it is undertaken for the purposes of the Capex Survey. This might be particularly problematic given the use of quarterly data.
Turning now to the different responses of incorporated and unincorporated businesses, the results from estimating the model separately for each business structure are in Table 7. They suggest that a 10 percentage point increase in the tax break leads to an increase in company investment of 12 per cent and an increase in unincorporated business investment of around 60 per cent. The p-value from a test of the equality of these coefficients is less than 1 per cent. This result aligns with our priors regarding the effects of dividend imputation.
| Companies | Unincorporated businesses (sole traders and partnerships) |
|
|---|---|---|
| η | 1.13*** (0.38) |
4.89*** (1.27) |
| Clusters (businesses) | 3,415 | 908 |
| Observations | 8,783 | 1,862 |
|
Notes: Control group is businesses of the same legal type with revenue $2–10 million; *** indicates significance at the 1 per cent level; standard errors are in parentheses and are clustered at the business level |
||
The estimated semi-elasticity for unincorporated businesses is broadly in line with estimates for small US companies in ZM (around 6.3). This is consistent with the fact that the US tax system does not allow for dividend imputation, and so is more comparable to the tax arrangements available to the owners of unincorporated businesses in Australia.
Interestingly, the estimate for companies is higher than the pooled estimate from above. Given the differing elasticities, this is not entirely surprising: large unincorporated businesses would be a poor control group for small companies, as they would respond quite strongly even to the 10 per cent tax break. Nevertheless, the estimated semi-elasticity for companies remains below the range estimated by the RD model.
Finally, Table 8 shows the results from the extensive margin model. The results indicate that a 10 percentage point increase in the tax break rate increases the odds of a business investing by 4 per cent. The average probability of a small business investing in a non-treatment quarter is 16 per cent, so the 50 per cent deduction for small businesses would raise the probability of investing to about 20 per cent. Again, the estimated effect is a bit larger when we use the broader control group.
As with the RD model, we can also examine whether businesses brought forward investment. We do this by including lags of the tax credit one and two years prior to the current quarter. If businesses simply brought forward investment, the coefficients on these variables should be negative and significant, as earlier higher levels of tax breaks should induce lower current investment. We focus on the intensive margin and find no evidence of statistically or economically significant intertemporal substitution of this type (Table 9).
| Control group | ||
|---|---|---|
| $2–10 million | > $2 million | |
| η | 0.43*** (0.01) |
1.10*** (0.02) |
| Clusters (ANZSIC division) | 14 | 14 |
| Business fixed effects | Yes | Yes |
| Observations | 61,210 | 117,759 |
|
Notes: *** indicates significance at the 1 per cent level; standard errors are in parentheses and are clustered at the industry level |
||
| Control group – $2–10 million | ||
|---|---|---|
| One lag of tax break | Two lags of tax break | |
| η | 0.87*** (0.31) |
0.96*** (0.32) |
| Tax break lagged one year | −0.36 (0.28) |
−0.25 (0.29) |
| Tax break lagged two years | 0.26 (0.30) |
|
| Clusters (businesses) | 5,724 | 5,724 |
| Business fixed effects | Yes | Yes |
| Observations | 14,379 | 14,379 |
|
Notes: *** indicates significance at the 1 per cent level; standard errors are in parentheses and are clustered at the business level |
||
6.3 Placebo Test
The Capex Survey dataset also provides information on building capex. As this type of capital expenditure was not covered by the investment tax break, it provides a natural setting for a placebo test of our DD strategy. If the parallel trends assumption is valid, equipment investment would have evolved similarly for the control and treatment groups in the absence of the tax break. As the tax break did not apply to building investment, this should still be the case even with the tax break. So re-running the model with building investment as the dependent variable should lead to estimates close to zero if the parallel trends assumption is valid.
Table 10 contains results for the baseline intensive margin model with building capex as the left-hand side variable. With the baseline control group, the response of building capex is close to zero. With the broader control group the response is larger, but is not statistically significant. A version of this model that includes equipment investment on the right-hand side – to control for potential complementarities or substitutability – provides similar results. This placebo test provides support for the parallel trends assumption, particularly for the narrow control group.
| Control group | ||
|---|---|---|
| $2–10 million | > $2 million | |
| η | 0.03 (1.03) |
0.56 (0.64) |
| Clusters (businesses) | 1,603 | 4,296 |
| Business fixed effects | Yes | Yes |
| Observations | 2,639 | 16,427 |
|
Note: Standard errors are in parentheses and are clustered at the business level |
||
The extensive margin placebo test has different results (Table 11). It indicates that small businesses, who received the largest tax breaks, were less likely to invest in buildings during the period in which the tax breaks were in place. One explanation could be that equipment and building investment are substitutes along the extensive margin. We try to account for this by including a variable that indicates whether or not businesses invested in equipment. However, when we do so the results suggest that building and equipment investment are, in fact, complements, and the estimate of η remains largely unchanged. It is still possible that the short-lived nature of the tax breaks caused building and equipment investment to become substitutes during the relevant period. But this seems unlikely given there is no evidence of such a change in the intensive margin placebo test.
| Control group | ||
|---|---|---|
| $2–10 million | > $2 million | |
| η | −0.69*** (0.03) |
−0.09*** (0.02) |
| Clusters (division) | 14 | 14 |
| Business fixed effects | Yes | Yes |
| Observations | 61,210 | 118,548 |
|
Notes: *** indicates significance at 1 per cent level; standard errors are in parentheses and are clustered at the division level |
||
The more likely explanation is that the parallel trends assumption does not hold for the extensive margin. It is plausible that this breach relates specifically to building investment, in which case it has no implications for our earlier results. For example, tighter borrowing conditions for small businesses may have affected building investment more than equipment investment due to the larger and lumpier nature of building investment. But, if it relates to both building and equipment investment, it indicates that our earlier results for the extensive margin were biased down and so understate the effect of the tax break.
6.4 Heterogeneous Responses by Business Size
ZM provide evidence that η is negatively correlated with business size – that is, small businesses respond more strongly to tax breaks. We analyse this by providing estimates from DD models that use different ranges of business size as the control group (Table 12). If the tax semi-elasticity for larger control groups is lower, estimates of η should increase with the size of the control group.
This is because the estimates should be increasingly upwardly biased, as the treatment group would be responding more than the control group to the 10 per cent tax break, even in the absence of the additional 40 percentage point tax break (the treatment). This exercise uses data for companies only, in order to abstract from differences across business legal types, and concentrates on the intensive margin.
| Control group | ||||||
|---|---|---|---|---|---|---|
| $2–10 million | $10–50 million | $50–100 million | $100–500 million | $500 million–$1 billion | > $1 billion | |
| η | 1.13*** (0.38) |
1.50*** (0.31) |
1.52*** (0.33) |
1.83*** (0.30) |
1.66*** (0.37) |
1.67*** (0.37) |
| Clusters (companies) | 3,415 | 4,337 | 3,441 | 3,872 | 2,662 | 2,500 |
| Company fixed effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 8,783 | 14,434 | 11,254 | 19,178 | 8,572 | 8,211 |
|
Notes: *** indicates significance at the 1 per cent level; standard errors are in parentheses and are clustered at the company level |
||||||
Estimated elasticities rise with the size of the control group used, up to around $500 million in revenue. However, the confidence intervals for most of the estimates overlap, suggesting that the coefficients cannot be statistically distinguished. So these results are somewhat consistent with the size heterogeneity found by ZM.[23]
The results of this exercise should be treated with caution. This is because it is unclear whether the differences in estimated semi-elasticities reflect differing elasticities, or other differences in economic and financial conditions between businesses of different sizes. The latter would likely bias our estimates downwards given most plausible trends in small and large business conditions during the GFC involve worse conditions for small businesses. For example, credit spreads for business lending rose during 2009, but by more for small businesses than for large (e.g. Hambur and La Cava 2018). Both the fact that these larger control groups pass placebo tests using building investment, and the fact that the estimated elasticities rise with business size, suggest the former explanation. In either case, the results support our choice to limit the baseline control group to businesses with revenue to $10 million.
6.5 Macroeconomic Effect
The estimated elasticity of aggregate equipment investment to the tax break can be used to calculate its macroeconomic effects. This elasticity can be obtained from a model using investment data aggregated to the division-by-business size level using sample weights provided by the ABS (see Appendix C for these results). This aggregation allows us to abstract from the separate effects of the tax break on businesses' investment at the extensive and intensive margins.[24]
We take the semi-elasticity estimated using businesses with revenue to $10 million as the control group to be our ‘true’ elasticity for all businesses with revenue less than $10 million. This elasticity is 1.76. Given the above evidence, we apply a lower elasticity to larger businesses using an ad hoc approach. We calculate this based on the difference between the estimated elasticity using the baseline control group, and that estimated using larger control groups. Specifically, we use the following formula: 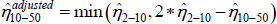 (e.g. for the $10 million to $50 million group). This formula restricts elasticities for the larger groups to be less than or equal to that for the baseline control group. In theory this method allows zero or negative elasticities for larger groups, if the results from the regressions with the control groups indicate that this is warranted. In practice, the adjusted elasticities range from 0.88–1.76.
(e.g. for the $10 million to $50 million group). This formula restricts elasticities for the larger groups to be less than or equal to that for the baseline control group. In theory this method allows zero or negative elasticities for larger groups, if the results from the regressions with the control groups indicate that this is warranted. In practice, the adjusted elasticities range from 0.88–1.76.
Applying these elasticities, we calculate that non-mining equipment capex would have been 29 per cent lower in 2009 if the investment tax break had not been in place. It is illustrative to translate this share of non-mining equipment capex into shares of other macroeconomic aggregates. Real private equipment investment in 2009 was $75.2 billion, and 29 per cent of this is $21.8 billion. If we adjust this down to account for the fact that around 25 per cent of investment in Australia is done using imported goods (Bussière et al 2013) and remove the remainder from 2009 real GDP, it implies year-average growth over 2009 of 0.5 per cent, well below actual growth of 1.7 per cent.[25] If this exercise is performed on a quarterly basis, real GDP declines in the March and June quarters of 2009 (actual GDP fell only in the December quarter of 2008). Using different elasticities for companies and unincorporated businesses (as well as size) changes this result only slightly. Using the elasticity from the RD model would massively increase the estimated effect of the tax break. But, given the estimate is very ‘local’, doing so seems inappropriate when estimating aggregate effects.
The above are partial equilibrium estimates. They do not account for other changes in the economy that would have occurred as a result of lower investment. If general equilibrium responses were included, it is likely that the reduction in GDP growth would be significantly smaller. Such general equilibrium responses include lower interest rates from a likely easing of monetary policy.
To account for general equilibrium effects, we use the dynamic stochastic general equilibrium model laid out in Gibbs, Hambur and Nodari (2018).[26] Without the additional investment induced by the tax break, adjusted down for the import share, the model suggests that year-ended GDP growth over 2009 would have been 0.8 per cent. In part, the smaller decline in GDP in this general equilibrium setting reflects additional monetary easing, with the model predicting that the cash rate would have been about 50 basis points lower in the absence of the investment tax break.
7. Future Directions for Research
Several facets of our results are worth discussing in the context of the academic literature. The fact that Australian companies responded to the tax break suggests that it worked through non-standard mechanisms. We provide no direct evidence on what these non-standard mechanisms might be, but a key candidate is a relaxation in company-level financial constraints. Future work could examine the particular mechanisms that underlie the response of Australian companies to the tax break. The datasets we use include many markers of financial constraints and so would be well suited to the analysis, but including these markers may require different identification methods.
In this context, it is worth noting that most of the large elasticity estimates in the literature are based on data from economic downturns, including the GFC. Financial constraints are likely to be particularly binding during such periods, which might make the investment incentives more effective than they would have been during ‘normal’ times. Further work examining the effect of similar policies in normal times could be useful, especially if policymakers want to use estimates from empirical studies to help them to evaluate future polices.
Further data-driven research on the effect of taxation on real business decisions in Australia seems worthwhile. For example, while our work suggests that tax rates and breaks can affect real decisions for Australian companies despite the existence of the dividend imputation system, it provides only limited guidance on the potential effects of permanent changes, such as a permanent cut to the company tax rate. The fact that we find no evidence of a fall in businesses' investment after the expiry of the policy suggests that permanent changes might have similar effects. But studies based on temporary and permanent policies in the United States have often generated quite different results (see discussion in House and Shapiro (2008)). Future Australian-focused studies could examine changes to simplified depreciation rules for small businesses from 2012, the sharp change to the depreciation schedule that occurred in 1999, or the change in company tax rates for small companies in 2015 (as examined in AlphaBeta (2018)).
8. Conclusion
Using two different statistical methods, we find that the investment tax break that the Australian Government introduced in response to the GFC substantially raised investment. Our results indicate that the tax breaks affected investment, at least in part, through non-standard mechanisms, such as by relaxing financial constraints.
We find no evidence that businesses brought forward investment from the future, indicating that the tax breaks led to an actual increase in the total amount of investment and, therefore, the capital stock. Moreover, based on our estimates of the size of the tax break's effects on aggregate investment and GDP, it should be considered an important part of Australia's macroeconomic history.
Appendix A: Data
The specific data items we use from BLADE are reported in businesses' business activity statements (BAS). The measure of investment we use is capital purchases, which includes plant and equipment, as well as land and buildings. It does not include intangible assets (ATO 2017a). We use total revenue as the measure of revenue. We exclude the mining division to abstract from the mining boom, and the finance division due to data issues.
The Capex Survey seeks responses from a sample of around 9,000 businesses each quarter. The largest businesses in Australia, roughly 3,000, are included in every quarter of the survey. This is necessary to accurately estimate aggregate capital expenditure, given the skewed distribution of capex. The capex of smaller businesses is estimated based on a random sample that is stratified by industry and size. For example, in a particular quarter, there were around 1,200 manufacturing businesses with between 50 and 99 employees in Australia. The survey sought responses from 10 of these businesses, and a weight of 120 was applied to each response when estimating total capex for this subset of businesses. Responses from the larger businesses that are always in the sample are assigned a weight of 1.
The design of the Capex Survey changed in the September quarter of 2009, in a way that is material for the analysis in this paper. Non-employing businesses were included in the survey population from this quarter. This generated an increase in aggregate estimates of capex, as estimates now approximated the capex of a larger set of businesses. Our primary approach to dealing with this change is to construct capex estimates for the population of employing businesses only. As with the BLADE data, we exclude businesses in the mining division to abstract from the direct effects of the mining boom (particularly in the graphical analysis).
| Mean | P10 | Median | P90 | Number of businesses | |
|---|---|---|---|---|---|
| Full sample | |||||
| Equipment capex ($'000) | 901 | 0 | 0 | 936 | 120,269 |
| Ln(equipment capex) | 12 | 8 | 12 | 15 | 58,856 |
| Building capex ($'000) | 729 | 0 | 0 | 25 | 120,269 |
| Ln(building capex) | 12 | 8 | 12 | 16 | 16,427 |
| Revenue ($'000) | 237,000 | 148 | 7,997 | 401,000 | 120,269 |
| Small business status (as a share of sample) | 40 | 0 | 0 | 100 | 120,269 |
| Small business | |||||
| Equipment capex ($'000) | 13 | 0 | 0 | 4 | 48,127 |
| Ln(equipment capex) | 9 | 7 | 9 | 11 | 8,617 |
| Building capex ($'000) | 78 | 0 | 0 | 25 | 48,127 |
| Ln(building capex) | 8 | 5 | 8 | 12 | 1,668 |
| Revenue ($'000) | 589 | 67 | 304 | 1,397 | 48,127 |
| Large business | |||||
| Equipment capex ($'000) | 1,493 | 0 | 50 | 2,071 | 72,142 |
| Ln(equipment capex) | 12 | 9 | 12 | 15 | 50,239 |
| Building capex ($'000) | 1,163 | 0 | 0 | 204 | 72,142 |
| Ln(building capex) | 12 | 9 | 12 | 16 | 14,759 |
| Revenue ($'000) | 395,000 | 4,807 | 60,000 | 698,000 | 72,142 |
|
Sources: ABS; Authors' calculations |
|||||
Appendix B: Extra RD Results
As noted in Section 5, for the RD specification we make a number of choices regarding the bandwidth, kernel, polynomial order and revenue ceiling. Below we show that the results are reasonably robust to these choices.
Figures B1 and B2 show the estimated treatment effects and 95 per cent confidence intervals using polynomials of order 1–4, with differing bandwidths. The results using a linear model are unsurprisingly somewhat sensitive to the choice of bandwidth, though they are not knife edge, as there is a moderate region around $0.2 million where the results are significant. Using higher-order polynomials we also find evidence of a significant treatment effect. These tend to be at higher bandwidths, reflecting the fact that we need a more flexible model once we look at a larger region. Importantly, the point estimates tend to be around 0.5–0.7, as in the baseline model. This gives us confidence that the results are reasonably robust.
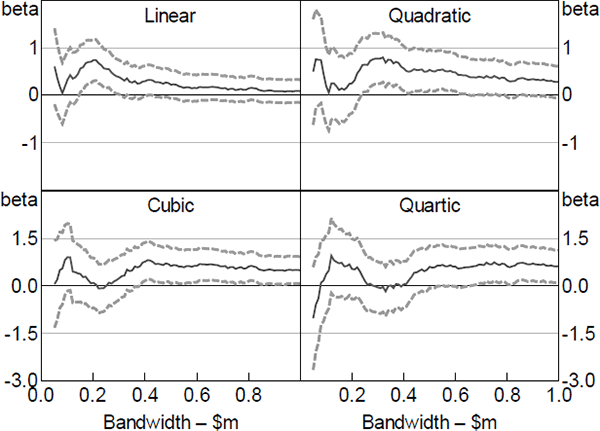
Notes: No covariates; bandwidth is 2007/08 revenue in $ million; dashed lines are 95 per cent confidence intervals
Figure B3 shows the estimated treatment effects and confidence intervals using the same bandwidth as in the baseline model, but with differing ceilings for revenue in 2008/09. Overall, the results are reasonably robust to this choice, as long as the ceiling is not set very low.
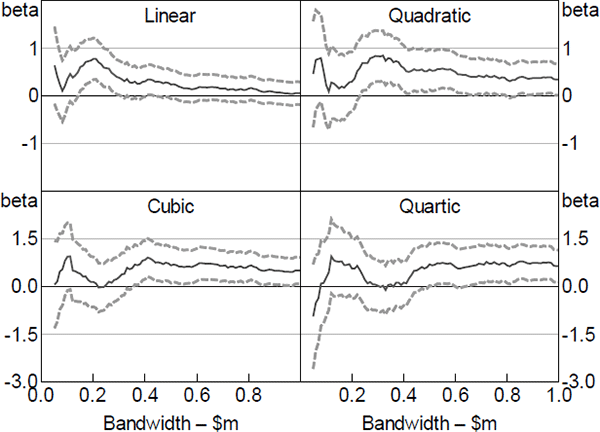
Notes: Notes: Includes revenue in 2008/09 and 2009/10 as covariates; bandwidth is 2007/08 revenue in $ million; dashed lines are 95 per cent confidence intervals
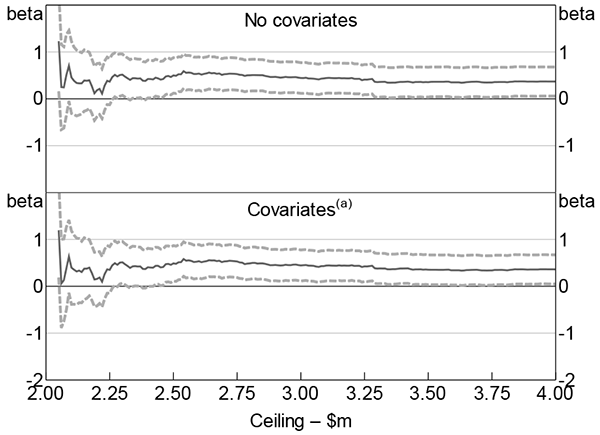
Notes:
Bandwidth set at baseline optimal of $0.27 million in 2007/08 revenue; ceiling is 2008/09 revenue in $ million; dashed lines are 95 per cent confidence intervals
(a) Includes revenue in 2008/09 and 2009/10
Appendix C: Extra DD Results
This appendix presents results from DD models using Capex Survey data aggregated to the division-by-business size level. The key difference from the business-level specification, Equation (1), is the replacement of the business fixed effects with ANZSIC division by size dummies.
| Control group | ||
|---|---|---|
| $2–10 million | > $2 million | |
| η | 1.76*** (0.57) |
2.04*** (0.36) |
| Clusters (division by size) | 28 | 98 |
| Observations | 504 | 1,750 |
|
Notes: *** indicates significance at the 1 per cent level; standard errors are in parentheses and are clustered at the division by size level |
||
Figure C1 shows the estimated aggregate elasticities using different control groups. These are the elasticities used to construct the estimates of the macroeconomic effects in Section 6.5.
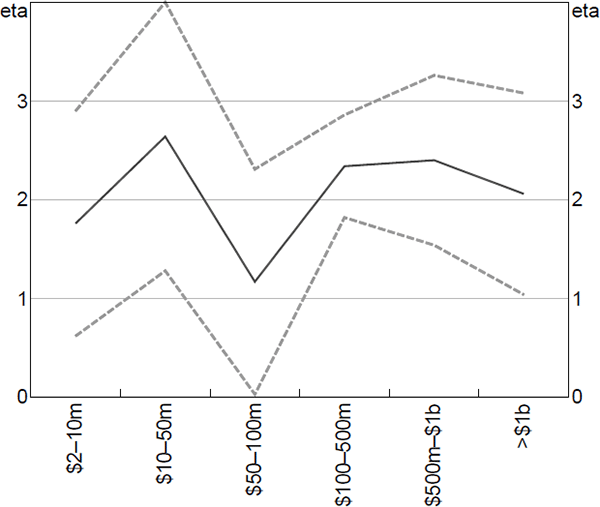
Note: Dashed lines are 95 per cent confidence intervals
Appendix D: Other Small Business Tax Policies
| Policy | Eligibility dependent upon small business status? | In force at the same time as investment tax break? |
| Capital gains concessions | No, businesses could qualify via $6m net asset value threshold | In force prior to and including investment tax break period |
| Accelerated depreciation for assets < $1,000 | Yes | In force prior to and including investment tax break period |
| Entrepreneurs tax offset | No, requires revenue < $75K | In force prior to and including investment tax break period |
| GST exemption | No, requires revenue < $75K | In force prior to and including investment tax break period |
| Reduction in intra-year tax instalments: 20% reduction in PAYG instalments for December quarter 2008 and CPI growth rate for PAYG and GST instalments during 2009/10 | No, businesses could qualify via assessable income (profit) < $2m | Yes |
References
AlphaBeta (2018), ‘Do Company Tax Cuts Boost Jobs, Wages and Investment?’, Report produced for Xero Small Business Insights, May. Available at <http://www.alphabeta.com/wp-content/uploads/2018/05/Xero-SBI-AlphaBeta-Tax-Report_May-2018.pdf>.
Atkin T and G La Cava (2017), ‘The Transmission of Monetary Policy: How Does It Work?’, RBA Bulletin, September, pp 1–8.
ATO (Australian Taxation Office) (2016), ‘Taxation Statistics 2013–14’, accessed 16 January 2018. Available at <https://data.gov.au/dataset/taxation-statistics-2013-14>.
ATO (2017a), ‘Step 3: Purchases’, viewed 16 January 2018. Available at <https://www.ato.gov.au/Business/GST/In-detail/Managing-GST-in-your-business/Reporting,-paying-and-activity-statements/GST---completing-your-activity-statement/?anchor=Step3Purchases#Step3Purchases>.
ATO (2017b), ‘Work Out if You're a Small Business for the Income Year’, viewed 22 December 2017. Available at <https://www.ato.gov.au/business/small-business-entity-concessions/eligibility/work-out-if-you-re-a-small-business-for-the-income-year/>.
Bussière M, G Callegari, F Ghironi, G Sestieri and N Yamano (2013), ‘Estimating Trade Elasticities: Demand Composition and the Trade Collapse of 2008–2009’, American Economic Journal: Macroeconomics, 5(3), pp 118–151.
Callen T, S Morling and J Pleban (1992), ‘Dividends and Taxation: A Preliminary Investigation’, RBA Research Discussion Paper No 9211.
Calonico S, MD Cattaneo and R Titiunik (2014), ‘Robust Nonparametric Confidence Intervals for Regression-Discontinuity Designs’, Econometrica, 82(6), pp 2295–2326.
Cattaneo MD, M Jansson and X Ma (2017), ‘Simple Local Polynomial Density Estimators’, Unpublished Manuscript, 27 September. Available at <http://www-personal.umich.edu/~cattaneo/papers/Cattaneo-Jansson-Ma_2017_LocPolDensity.pdf>.
Clark JM (1917), ‘Business Acceleration and the Law of Demand: A Technical Factor in Economic Cycles’, Journal of Political Economy, 25(3), pp 217–235.
Cockerell L and S Pennings (2007), ‘Private Business Investment in Australia’, RBA Research Discussion Paper No 2007-09.
Cohen D and J Cummins (2006), ‘A Retrospective Evaluation of the Effects of Temporary Partial Expensing’, Board of Governors of the Federal Reserve System Finance and Economics Discussion Series No 2006-19.
Coorey P (2018), ‘Labor Promises New Tax Write-Offs for Business’, Australian Financial Review online, 13 March, viewed 18 April 2018. Available at <http://www.afr.com/news/labor-promises-new-tax-writeoffs-for-business-20180312-h0xduq>.
Cummins JG, KA Hassett and RG Hubbard (1994), ‘A Reconsideration of Investment Behavior Using Tax Reforms as Natural Experiments’, Brookings Papers on Economic Activity, 2, pp 1–59, 70–74.
Dixon JM and J Nassios (2016), ‘Modelling the Impacts of a Cut to Company Tax in Australia’, Centre of Policy Studies Working Paper No G-260.
Economist, The (2017), ‘Will Corporate Tax Cuts Boost Workers’ Wages?', The Economist online, 26 October, viewed 11 March 2018. Available at <https://www.economist.com/news/finance-and-economics/21730696-white-house-report-puts-economists-each-others-throats-will-corporate-tax-cuts>.
Gibbs CG, J Hambur and G Nodari (2018), ‘DSGE Reno: Adding a Housing Block to a Small Open Economy Model’, RBA Research Discussion Paper No 2018-04.
Goolsbee A (1998), ‘Investment Tax Incentives and the Price of Capital Goods’, The Quarterly Journal of Economics, 113(1), pp 121–148.
Hall RE and DW Jorgenson (1967), ‘Tax Policy and Investment Behavior’, The American Economic Review, 57(3), pp 391–414.
Hambur J and G La Cava (2018), ‘Do Interest Rates Affect Business Investment? Evidence from Australian Company-Level Data’, RBA Research Discussion Paper No 2018-05.
Hansell D and B Rafi (2018), ‘Firm-Level Analysis Using the ABS’ Business Longitudinal Analysis Data Enviroment (BLADE)', The Australian Economic Review, 51(1), pp 132–138.
Hassett KA and RG Hubbard (2002), ‘Tax Policy and Business Investment’, in AJ Auerbach and M Feldstein (eds), Handbook of Public Economics: Volume 3, Handbooks in Economics 4, Elsevier, Amsterdam, pp 1293–1343.
House CL and MD Shapiro (2008), ‘Temporary Investment Tax Incentives: Theory with Evidence from Bonus Depreciation’, The American Economic Review, 98(3), pp 737–768.
Imbens GW and K Kalyanaraman (2012), ‘Optimal Bandwidth Choice for the Regression Discontinuity Estimator’, The Review of Economic Studies, 79(3), pp 933–959.
Imbens GW and T Lemieux (2008), ‘Regression Discontinuity Designs: A Guide to Practice’, Journal of Econometrics, 142(2), pp 615–635.
Kouparitsas M, D Prihardini and A Beames (2016), ‘Analysis of the Long Term Effects of a Company Tax Cut’, Australian Treasury, Treasury Working Paper No 2016-02.
La Cava G (2005), ‘Financial Constraints, the User Cost of Capital and Corporate Investment in Australia’, RBA Research Discussion Paper No 2005-12.
Lee DS and T Lemieux (2010), ‘Regression Discontinuity Designs in Economics’, Journal of Economic Literature, 48(2), pp 281–355.
Leigh A (2012), ‘How Much Did the 2009 Australian Fiscal Stimulus Boost Demand? Evidence from Household-Reported Spending Effects’, The B.E. Journal of Macroeconomics, 12(1), Contributions, Article 4.
Li SM and AH Spencer (2016), ‘Effectiveness of the Australian Fiscal Stimulus Package: A DSGE Analysis’, Economic Record, 92(296), pp 94–120.
Makin T (2016), ‘The Effectiveness of Federal Fiscal Policy: a Review’, Treasury Research Institute External Paper No 2016-01.
Officer RR (1994), ‘The Cost of Capital of a Company under an Imputation Tax System’, Accounting & Finance, 34(1), pp 1–17.
Reinhardt S and L Steel (2006), ‘A Brief History of Australia's Tax System’, Economic Roundup, Winter, pp 1–26.
Rodgers D (2017), ‘The GFC Investment Tax Credit’, in ‘Private New Capital Expenditure and Expected Expenditure, Australia, March Quarter 2017’, ABS Cat No 5625.0.
Senate (Senate Economics References Committee) (2009), Government's Economic Stimulus Initiatives, (A Eggleston, Chair), Commonwealth of Australia, Canberra.
Sraer D and D Thesmar (2018), ‘A Sufficient Statistics Approach for Aggregating Firm-Level Experiments’, NBER Working Paper No 24208.
Swan PL (2018), ‘Investment, the Corporate Tax Rate, and the Pricing of Franking Credits’, Unpublished Manuscript, UNSW Business School, March.
Swan W (Treasurer) (2008), ‘Investment Allowance to Boost Business Investment’, Press Release No 141, Canberra, 12 December.
Swan W (Treasurer) (2009a), ‘Small Business and General Business Tax Break’, Press Release No 013, Joint Media Release with the Prime Minister and Minster for Small Business, Canberra, 3 February.
Swan W (Treasurer) (2009b), ‘Small Business Tax Break Boost’, Press Release No 061, Joint Press Release with the Hon Dr Craig Emerson MP Minister for Small Business, Independent Contractors and the Service Economy, Canberra, 12 May.
Tingle L and P Coorey (2018), ‘Scott Morrison Talks up Wage Benefits of Company Tax Cut’, Australian Financial Review online, 4 February, viewed 11 March 2018. Available at <http://www.afr.com/news/scott-morrison-talks-up-wage-benefits-of-company-tax-cut-20180204-h0tcic>.
Twite G (2001), ‘Capital Structure Choices and Taxes: Evidence from the Australian Dividend Imputation Tax System’, International Review of Finance, 2(4), pp 217–234.
Zwick E and J Mahon (2017), ‘Tax Policy and Heterogeneous Investment Behavior’, The American Economic Review, 107(1), pp 217–248.
Copyright and Disclaimer Notice
BLADE Disclaimer
The results of these studies are based, in part, on ABR data supplied by the Registrar to the ABS under A New Tax System (Australian Business Number) Act 1999 and tax data supplied by the ATO to the ABS under the Taxation Administration Act 1953. These require that such data are only used for the purpose of carrying out functions of the ABS. No individual information collected under the Census and Statistics Act 1905 is provided back to the Registrar or ATO for administrative or regulatory purposes. Any discussion of data limitations or weaknesses is in the context of using the data for statistical purposes, and is not related to the ability of the data to support the ABR or ATO's core operational requirements. Legislative requirements to ensure privacy and secrecy of this data have been followed. Only people authorised under the Australian Bureau of Statistics Act 1975 have been allowed to view data about any particular firm in conducting these analyses. In accordance with the Census and Statistics Act 1905, results have been confidentialised to ensure that they are not likely to enable identification of a particular person or organisation.
Acknowledgements
David Rodgers completed much of this work while on secondment from the RBA to the Australian Bureau of Statistics. We would like to thank the Australian Bureau of Statistics for providing data access, advice and assistance during the preparation of this paper. We would also like to thank Christian Gillitzer, James Bishop, Matthew Shapiro, Gianni La Cava, Ben Ralston, Michelle van der Merwe and John Simon for useful comments and suggestions, as well as seminar participants at the RBA, the UNSW Macroeconomics Reading Group, and the Australian Treasury. The views expressed in this paper are those of the authors and do not represent those of any institution. All errors are our own.
Footnotes
Economic Research Department, Reserve Bank of Australia and UNSW Sydney [*]
Economic Research Department, Reserve Bank of Australia [**]
The United States, the Netherlands, and South Korea used investment tax incentives during the global financial crisis (GFC). More recently, the 2017 US tax reform incorporates a significant investment tax incentive (full expensing). A similar policy has recently been suggested in Australia (Tingle and Coorey 2018). [1]
See The Economist (2017), and for an Australian perspective, Coorey (2018). [2]
See Atkin and La Cava (2017) for a discussion of the ‘saving and investment’, or intertemporal substitution, channel. [3]
Currently, only New Zealand, Chile and Mexico have dividend imputation systems comparable to that in Australia. Other OECD countries have had dividend imputation in the past. [4]
See Leigh (2012) and Li and Spencer (2016) for studies of the other components of the stimulus. The investment tax break is mentioned in a Senate inquiry into the effectiveness of the stimulus held in late 2009 (Senate 2009), but received almost no attention in a recent review of the stimulus (Makin 2016). [5]
See the Copyright and Disclaimer Notice. [6]
The tax credit applied to depreciating assets for which deductions were available under Subdivision 40-B of the Income Tax Assessment Act 1997. This subdivision captures most equipment investment. Building investment is generally dealt with under another section of the Income Tax Assessment Act 1997 (the capital works expenditure rules). [7]
See Section 328-110 of the Income Tax Assessment Act 1997 as in force 29 May 2009; <https://www.legislation.gov.au/Details/C2009C00226>. [8]
For discussions of the theory and practice of the RD approach, see, for example, Imbens and Lemieux (2008) and Lee and Lemieux (2010). [9]
The tax break also differed for the final 1.5 months of 2008/09. We discuss this in Section 5.3 below. [10]
Businesses not registered for the goods and services tax (GST) are not included in the dataset. Very small businesses, that either never have sales above $75,000, or that never employ a worker, are removed from the dataset. [11]
For details on the particular data we use, see Appendix A. [12]
We could estimate a DD model using the BLADE data to examine these heterogeneities. But we prefer to use the Capex Survey given it differentiates between investment types and is available at a quarterly frequency, which allows us to exploit quarter-to-quarter variation in the deduction rates. BLADE data are only available at an annual frequency. [13]
They suggest including a full set of bin dummies in the regression, and jointly testing whether the coefficients are zero. The advantage of this approach is that it would also pick up other discontinuities in investment. [14]
Clustering the errors by 4-digit ANZSIC group leads to slightly higher p-values, but does not change the significance of the results. [15]
Unless the covariates have very high explanatory power, their inclusion should not affect the optimal bandwidth (Imbens and Kalyanaraman 2012). As such, we use the same bandwidth for these models. [16]
We also tried using their bandwidth selection rules and variance estimator, as implemented using the Stata ‘rdrobust’ package. The estimated treatment effects were generally around 0.5–0.6 across a number of specifications with different kernels and covariates. [17]
Some US corporates (S corporations) are taxed on a pass-through basis akin to the treatment of unincorporated businesses in Australia. [18]
The latter also suggests that businesses did not ‘fund’ the investment by substituting away from labour. This is broadly consistent with the findings in ZM, though they actually find that employment increased. [19]
So it is log 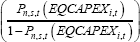 . The four granular turnover categories are those shown in Figure 7.
[20]
. The four granular turnover categories are those shown in Figure 7.
[20]
The variable is equivalent to the discounted cash flow measure used in ZM, given that for the Australian investment tax break the full tax benefit accrues in the first year. [21]
The regressions are unweighted, so we are effectively treating the responses underlying the Capex Survey as a simple random sample. Weighted regressions that use the Capex Survey sample weights, and models that exclude the large businesses that are always selected into the sample, generate similar results. [22]
An interesting feature of the results is that the estimated semi-elasticities actually decline for very large companies – with revenue above $500 million – indicating that these companies responded more strongly to the tax breaks than companies with revenue of $100 to $500 million. This is consistent with very large companies having more foreign investors, and therefore a lower γ in their user cost, making their costs of capital more sensitive to the tax break. [23]
While these aggregate results indicate that building and equipment investment are complements, we abstract from any potential positive spillovers to building investment in this analysis. [24]
Equipment investment is likely to be more import-intensive than other types of investment, such as non-residential construction. As such, the adjustment we make is probably too small, and so the effects of the tax break are likely to be a bit overstated. [25]
The approach suggested in Sraer and Thesmar (2018) offers another potential way forward here. [26]