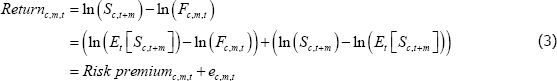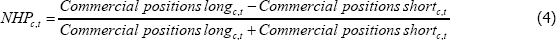RDP 2017-03: Financialisation and the Term Structure of Commodity Risk Premiums 3. Data and Measurement of Commodity Risk Premiums
May 2017
3.1 Risk Premiums
As discussed above, commodity risk premiums can be defined as the difference between the expected spot price at some specific future date and the price set for a futures contract maturing at that same date. Ideally, commodity risk premiums would be measured ex ante using information on market participants' expectations for the spot price. However, a dataset containing time series of price expectations across a series of forecast horizons and for a broad range of commodities is not readily available. A commonly used alternative is to measure risk premiums ex post by calculating the average annualised return on a futures contract. We measure this as the return from buying a futures contract and settling that contract at expiration.
The realised (continuously compounded) return for any futures contract will be the risk premium plus any unexpected deviation of the observed spot price at expiry from the expected future spot price (as at the purchase date):[18]
Assuming investors' expectations are unbiased, the unexpected deviation (ec,m,t) should average zero in a long enough sample.[19] Therefore, on average the return should be equal to the risk premium.
A dataset of futures contracts was constructed for 26 commodities for the period 1986–2014 (where available).[20] These were then used to calculate returns.[21] Consistent with most previous studies, we find that non-zero individual commodity risk premiums on short-dated contracts (e.g. one- to three-month maturities) are hard to identify statistically (Table 1).
| 1-month | 3-month | 6-month | 9-month | 12-month | |
|---|---|---|---|---|---|
| Agriculture | |||||
| Coffee | 13.4 | −4.3 | −6.6 | −5.7 | −7.2* |
| Corn | −5.4 | −4.2 | −5.8 | −4.5 | −3.5 |
| Cotton | −6.4 | −2.4 | −3.9 | −1.6 | −1.1 |
| Lean hogs | 3.8 | −0.5 | 3.4 | 3.6 | 3.7 |
| Live cattle | 13.0*** | 7.2*** | 5.5*** | 4.6*** | 3.7*** |
| Lumber | −11.0 | −7.5 | −7.2* | −4.7 | 1.4 |
| Milk | 4.0 | 4.3 | 2.3 | 2.8 | 3.7 |
| Orange juice | 9.6 | 1.5 | −2.0 | −2.9 | −3.7 |
| Soybeans | 11.0* | 6.2 | 4.2 | 4.8* | 4.0* |
| Soybean meal | 13.1** | 11.2*** | 9.4*** | 8.7*** | 7.7*** |
| Wheat (Minnesota) | 8.8 | 6.0 | 2.5 | 2.3 | 2.5 |
| Wheat (SRW) | 6.5 | −2.6 | −3.9 | −2.7 | −2.5 |
| Energy | |||||
| Heating oil | 9.0 | 6.8 | 7.0 | 7.5* | 7.5* |
| Natural gas | −16.3 | −14.6 | −9.3 | −6.8 | −3.9 |
| WTI crude oil | 5.7 | 6.7 | 7.4 | 8.0* | 8.4** |
| Metals | |||||
| Copper | 6.7 | 5.9 | 5.3 | 6.2 | 6.9* |
| Palladium | 2.8 | 6.5 | 9.2* | 9.3** | 5.0 |
| Platinum | 15.5 | 6.5 | 5.1 | 2.7 | −0.3 |
|
Notes: SRW denotes soft red wheat; sample period 1986–2014; *, ** and *** indicate returns are significantly different from zero at the 10, 5 and 1 per cent level, respectively; standard errors are robust to serial correlation and heteroskedasticity |
|||||
However, in a number of cases we can identify both economically and statistically significant risk premiums on longer-dated futures contracts (e.g. nine- to twelve-month maturities). Further, Figure 4 shows that for a given commodity, the risk premium is typically not constant across futures contracts with different maturities, and the shape of the ‘risk premium curve’ differs substantially across commodities.[22]
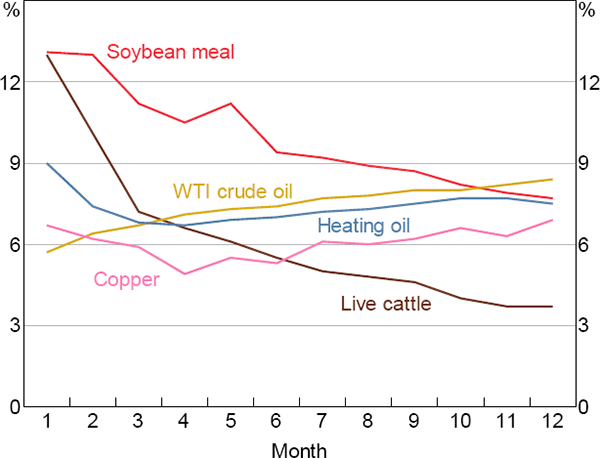
Notes: Average annualised return from buying a futures contract and selling it at expiration; sample period 1986–2014
Sources: Authors' calculations; Pinnacle Data
3.2 Net Hedging Positions
Our NHP is constructed using CFTC data on commercial positions in futures contracts traded on futures exchanges. The CFTC defines a ‘commercial’ position as one belonging to a participant that uses the futures market to hedge exposures that arise as part of their usual operations. As such, it includes positions of producers and consumers, but also of swap dealers who act as intermediaries in these markets. This will introduce some noise into the measure as, while swap dealers often act as intermediaries for producers and consumers, they can also act as intermediaries for speculators.[23]
We define NHP to be net commercial positions, scaled by gross commercial positions, or:
NHP is commodity specific, but not contract specific. That is, while NHP at time t differs between oil and copper, it does not differ between an oil futures contract with a one-month maturity and an oil futures contract with a two-month maturity. This is not ideal, as the NHP for a particular maturity is purported to be the determinant of the risk premium on that commodity futures contract. Using aggregated NHP data could mask differences in the net hedging pressure at different maturities as it is unlikely that the NHP is roughly equal across all maturities. This could make it harder to identify a significant relationship between NHP and risk premiums. Unfortunately, data on commercial positions by maturity are not publically available.
Footnotes
For a full derivation, see Appendix A. [18]
As defined here, Et (ec,m,t) will differ from zero by a small amount due to Jensen's inequality. [19]
For a list of the commodities, see Appendix B. [20]
For more details, see Appendix C. [21]
The upwards slope of the risk premium curve for oil is consistent with Singleton (2014), who finds average weekly returns for longer-dated oil future contracts are higher. [22]
Swap dealers act as intermediaries by entering over-the-counter derivatives contracts. They may then hedge their net exposures using futures markets. For more details, see CFTC (2008). [23]