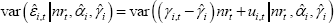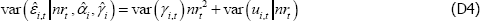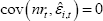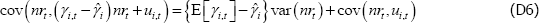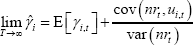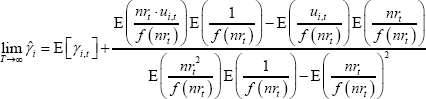RDP 2016-11: Identifying Interbank Loans from Payments Data Appendix D: Derivation of the Model

For simplicity, this appendix assumes that there are no rollovers and that there is no persistence in u_i,t. The intuition when rollovers and persistence are included is the same. Suppose the true data-generating process is (where γ_i,t is the ‘net share’ in session i of day t):

With the net share varying over time, u_i,t consists of loan-identification errors only. However, suppose we estimate:

Then, by combining Equations (D1) and (D2):

Estimating a constant net share causes the conditional variance of 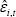(conditional on nr_t, 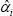and 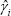to differ from the variance that does not condition on nr_t:

Assuming changes in γ_i,t are independent of both nr_t and u_i,t:

Equation (D4) justifies the functional form we assume for the conditional heteroskedasticity in our model.

Now suppose the parameters are estimated using ordinary least squares (OLS). By construction, the estimated sample covariance between nr_t and 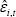will be zero. Assuming the conditions required for the weak law of large numbers hold, the sample covariance converges in probability to the population covariance. Therefore, the following holds for the population covariance:

Which, using Equation (D3), can be rewritten as:

If γ_i,t and nr_t are independent, then the population covariance can be expanded to:

Using Equations (D5) and (D6), and re-arranging, gives the following limit value for 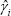(i.e. as T → ∞, where T is the sample size):

So, in the limit, the OLS estimator of the constant net share (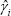) will equal the mean of the net share plus a bias term caused by any correlation between non-rolled loans and the loan-identification error.

If the bias term is non-zero, then an estimator for 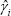that accounts for the conditional heteroskedasticity of 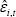(such as the Gaussian maximum likelihood estimator (MLE) used in Section 5.3) will, in general, converge to a different point than the OLS estimator. However, it can be shown that the point of convergence of the Gaussian MLE will have the same form as the OLS estimator; being equal to the mean of the net share plus a bias term:

where f(nr_t) is the limiting conditional variance of 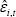. This bias term equals the bias term for the OLS estimator if f(nr_t) is a constant. As with the OLS bias term, this bias term will equal zero if nr_t and u_i,t are uncorrelated.