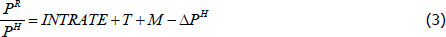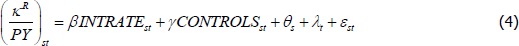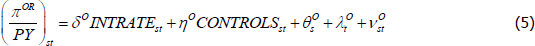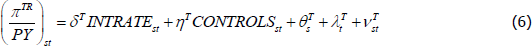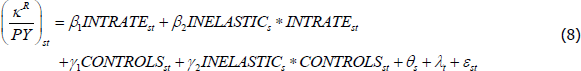RDP 2016-04: Housing Prices, Mortgage Interest Rates and the Rising Share of Capital Income in the United States 5. Statistical Evidence
May 2016
- Download the Paper 1.13MB
5.1 Housing Income and Mortgage Interest Rates
To explore the determinants of the secular rise in housing capital income, and highlight the key role of the trend decline in interest rates, I estimate a state-level panel regression model. The specification of the model is motivated by the housing user cost of capital literature (Poterba 1984; Díaz and Luengo-Prado 2008). Loosely speaking, the user cost model relates the ratio of rents to housing prices to factors including mortgage interest rates, property taxes, maintenance costs and expected capital gains on housing. More formally:
where the rent-to-housing price ratio 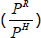 is a function of the nominal mortgage rate (INTRATE), property taxes (T),
maintenance costs (M) and expected housing capital gains (ΔPH).
Note that the user cost formula implies that correlation between mortgage interest rates and the
rent-to-house price ratio is positive. This is because of the underlying arbitrage
condition which implies that a housing investor (including owner-occupiers) should be
indifferent at the margin between purchasing a home (and earning the rental yield) and investing
in alternative assets, such as a bank deposit (and earning the interest rate).[10]
My main focus is on the correlation between mortgage rates and the share of housing capital
income, so I absorb the other terms into a set of control variables and specify a regression
model of the form:
is a function of the nominal mortgage rate (INTRATE), property taxes (T),
maintenance costs (M) and expected housing capital gains (ΔPH).
Note that the user cost formula implies that correlation between mortgage interest rates and the
rent-to-house price ratio is positive. This is because of the underlying arbitrage
condition which implies that a housing investor (including owner-occupiers) should be
indifferent at the margin between purchasing a home (and earning the rental yield) and investing
in alternative assets, such as a bank deposit (and earning the interest rate).[10]
My main focus is on the correlation between mortgage rates and the share of housing capital
income, so I absorb the other terms into a set of control variables and specify a regression
model of the form:
where the dependent variable is housing capital income as a share of total nominal GDP 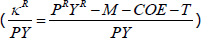 for
state s in t. (Recall that housing capital income at the state level is
proxied using the gross operating surplus of the real estate sector). The key explanatory
variable is the average level of nominal interest rates on new mortgage debt (INTRATE).
The control variables (CONTROLS) include current annual growth in housing prices (as a
proxy for expected capital gains) and average property taxes.
for
state s in t. (Recall that housing capital income at the state level is
proxied using the gross operating surplus of the real estate sector). The key explanatory
variable is the average level of nominal interest rates on new mortgage debt (INTRATE).
The control variables (CONTROLS) include current annual growth in housing prices (as a
proxy for expected capital gains) and average property taxes.
The user cost formula relates specifically to the price of rent, whereas I am interested in
explaining the share of nominal income going to rent 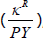 ,
which, as discussed earlier, is a function of the relative price of rent
,
which, as discussed earlier, is a function of the relative price of rent 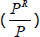 and the relative volume of rent
and the relative volume of rent 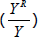 . As such, I also
include demand-side variables that might be expected to influence both the relative price and
relative volume of rent, including population growth and real GDP growth.[11]
. As such, I also
include demand-side variables that might be expected to influence both the relative price and
relative volume of rent, including population growth and real GDP growth.[11]
The specification includes state fixed effects (θs) to control for factors that do not vary with time but potentially determine the proportion of income spent on both market and imputed rent, such as the desirability of the location (e.g. local amenities or distance to the coast).
The model also includes year fixed effects (λt) that control for factors related to the national business cycle (e.g. monetary policy). These fixed effects will absorb all the aggregate time-series variation in each variable, including the net housing capital income share, mortgage interest rates and housing prices. To demonstrate the importance of the time fixed effects I also separately estimate the model with the inclusion of the aggregate federal funds rate (to control for monetary policy) rather than time fixed effects.[12]
I also estimate the same panel regression model but switch the dependent variable from gross housing capital income (as a share of GDP) to net housing profit income (as a share of GDP). This allows for a separate examination of the effect of mortgage interest rates on the income flowing to both owner-occupied and tenant-occupied housing (as the BEA provides these data separately at the state level) as follows:
where I estimate separate regressions for the profits on owner-occupied housing (πOR) and tenant-occupied housing (πTR). All the explanatory variables are as before.
By comparing the estimated effect of mortgage interest rates on housing profit income (πOR) for owner-occupiers and overall housing capital income (κR) we can also gauge the relative importance of the different channels through which interest rates can affect the income flowing to owner-occupiers. Interest rates should have a stronger effect on the net profits of owner-occupiers than on housing capital income. Lower interest rates will boost both net profits and net capital income to the extent that they push up housing prices, but lower interest rates will have an additional effect of increasing net profits by also reducing debt-servicing costs.
The results of estimating Equations (4), (5) and (6) are shown in Table 3. The first three columns show the estimates for housing capital income (κR). The following three columns show the estimates for net housing profits for owner-occupied housing (πOR). The final three columns show the estimates for net housing profits for tenant-occupied housing (πTR).
| Net housing capital income | Net owner-occupied housing profits | Net tenant-occupied housing profits | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |||
| Interest rate | −0.178*** (−6.32) |
−0.082*** (−3.15) |
−0.222* (−1.76) |
−0.203*** (−29.55) |
−0.210*** (−20.19) |
−0.013 (−0.41) |
−0.020*** (−5.90) |
0.015*** (3.78) |
−0.035 (−1.47) |
||
| Housing price growth | −0.030*** (−5.72) |
−0.014* (−1.78) |
−0.003 (−1.15) |
−0.002 (−1.10) |
−0.011*** (−7.85) |
−0.003** (−2.30) |
|||||
| Real GDP growth | −0.052*** (−5.57) |
−0.054*** (−4.64) |
−0.021*** (−6.32) |
−0.007** (−2.41) |
0.001 (0.52) |
−0.005* (−1.84) |
|||||
| Population growth | −0.143*** (−3.07) |
−0.145*** (−2.76) |
−0.016 (−0.53) |
−0.029 (−1.32) |
0.019 (1.29) |
0.011 (0.64) |
|||||
| Federal funds rate | −0.049** (−2.19) |
0.007 (1.23) |
−0.021*** (−8.56) |
||||||||
| State fixed effects | No | Yes | Yes | No | Yes | Yes | No | Yes | Yes | ||
| Year fixed effects | No | No | Yes | No | No | Yes | No | No | Yes | ||
| R2 | 0.055 | 0.272 | 0.339 | 0.605 | 0.647 | 0.927 | 0.033 | 0.230 | 0.611 | ||
| Observations | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | ||
|
Notes: Standard errors are clustered by state; Hausman tests reject the assumption of random state fixed effects; the sample period is that underpinning the regression estimates, which covers the years from 1978 to 2012; ***, **, and * denote significance at the 1, 5 and 10 per cent level, respectively; t statistics in parentheses |
|||||||||||
The results generally indicate that there is a negative correlation between nominal mortgage interest rates and the share of housing income. A 100 basis point decline in nominal mortgage interest rates is associated with the share of housing capital income rising by between 8 basis points (column 2) and 22 basis points (column 3), on average, depending on the regression specification. The same-sized decline in interest rates is also associated with net profits to home owners rising by between 1.3 basis points (column 6) and 21 basis points (column 5), on average. In contrast, there is some tentative evidence that lower interest rates are associated with lower net profits for landlords (column 8). Recall from Equation (3) that the user cost model points to a positive relationship between interest rates and the rental yield, which is suggestive of the user cost model being more applicable in practice to landlords than to home owners.
Given that interest rates fell, on average, at an annual rate of 17 basis points and the share of housing capital income rose by 7.4 basis points, on average, over the sample period, the results in column 3 suggest that lower nominal interest rates could explain around half the long-run rise in the share of housing capital income (i.e. 0.506 = (−0.17 * −0.222)/0.074).
Perhaps the most striking feature of these results is the fact that the negative correlation between mortgage interest rates and housing capital income generally persists even after controlling for changes in monetary policy through the inclusion of year fixed effects (columns 3, 6 and 9). This is remarkable given that there is limited variation in mortgage interest rates across states, with most of the variation coming from the time series.
If we compare across similar model specifications (e.g. columns 2 and 5 or columns 3 and 6), there is some evidence that the correlation between interest rates and the share of owner-occupier profits is economically larger than the same correlation between interest rates and the share of housing capital income. For example, in the model with the federal funds rate, the coefficient estimate is −0.210 for owner-occupier profits (column 5) and −0.082 for housing capital income (column 2). This provides some evidence that lower interest rates affect net housing income through two channels: through their indirect effect on housing demand (apparent in both models) and their direct effect on debt-servicing costs (only apparent in the owner-occupier profit model).[13]
The coefficient estimate on expected housing capital gains (as proxied by current housing price growth) is, in general, negatively signed, which is consistent with the user cost of capital model. The coefficient estimates on the other control variables are somewhat surprising. In general, we would expect higher GDP and population growth to be associated with higher housing demand, and hence a greater share of the state economy going to the housing sector. But the estimates generally point to the opposite, with both growth in real GDP and the population being negatively correlated with the share of income going to housing.
5.2 Housing Income, Real Interest Rates and Consumer Price Inflation
Next, I estimate a specification in which I decompose the nominal interest rate into two components using the Fisher equation: 1) the real interest rate; and 2) consumer price inflation:[14]
where the key explanatory variables are the average level of real interest rates on new mortgage debt (RINTRATE) and average CPI inflation (ΔCPI). This allows for an examination of the channels through which changes in nominal interest rates might have affected the housing capital income share. In particular, if financial deregulation was important we might expect to observe a negative correlation between real interest rates and the housing capital income share, while if disinflation mattered we should observe a negative correlation between CPI inflation and the share of housing capital income.[15] Again, I estimate separate models for net housing capital income and profits.
The results of estimating Equation (7) are shown in Table 4. The decomposition of nominal interest rates into real interest rates and inflation suggests that both factors are negatively correlated with the share of housing income. This is true even after allowing for monetary policy changes through the inclusion of the federal funds rate (columns 2, 5 and 8). However, the inclusion of time dummies results in the estimated coefficients on both terms generally being outside traditionally accepted levels of statistical significance (columns 3, 6 and 9).
Over the sample period, I estimate that consumer price inflation fell by more than the level of real interest rates, on average. Moreover, the coefficient estimate on inflation is, in general, about the same (or slightly larger) than the coefficient estimate on the real interest rate. Taken together, this provides some evidence that lower inflation is more economically important than lower real interest rates in explaining the secular rise in the share of housing capital income.[16]
| Net housing capital income | Net owner-occupied housing profits | Net tenant-occupied housing profits | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |||
| Real interest rate | −0.162*** (−5.88) | −0.124*** (−4.36) | −0.226* (−1.72) | −0.215*** (−30.65) | −0.214*** (−18.26) | −0.016 (−0.49) | −0.005 (−1.59) | 0.001 (0.17) | −0.036 (−1.44) | ||
| CPI inflation | −0.199*** (−6.29) | −0.160*** (−4.28) | −0.072 (−0.48) | −0.204*** (−28.22) | −0.197*** (−14.56) | −0.060 (−1.37) | −0.030*** (−8.10) | −0.016*** (−3.06) | −0.027 (−0.96) | ||
| Housing price growth | −0.026*** (−4.47) | −0.020** (−2.35) | −0.003 (−1.33) | −0.001 (−0.41) | −0.010*** (−6.65) | −0.004** (−2.45) | |||||
| Real GDP growth | −0.057*** (−6.24) | −0.054*** (−4.86) | −0.021*** (−6.33) | −0.007** (−2.41) | 0.001 (−0.28) | −0.005* (−1.86) | |||||
| Population growth | −0.137*** (−2.95) | −0.149*** (−2.84) | −0.018 (−0.62) | −0.028 (−1.31) | 0.022 (1.43) | 0.010 (0.63) | |||||
| Federal funds rate | −0.008 (−0.48) | −0.002 (−0.29) | −0.004* (−1.74) | ||||||||
| State fixed effects | No | Yes | Yes | No | Yes | Yes | No | Yes | Yes | ||
| Year fixed effects | No | No | Yes | No | No | Yes | No | No | Yes | ||
| R2 | 0.058 | 0.278 | 0.342 | 0.606 | 0.650 | 0.928 | 0.073 | 0.258 | 0.612 | ||
| Observations | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | ||
|
Notes: Standard errors are clustered by state; the sample period is that underpinning the regression estimates, which covers the years from 1978 to 2012; ***, **, and * denote significance at the 1, 5 and 10 per cent level, respectively; t statistics in parentheses |
|||||||||||
5.3 Housing Income, Interest Rates and Supply Constraints
If lower interest rates contributed to more income being spent on housing then we would also expect this effect to be particularly strong in states that are constrained in terms of land supply. To test this hypothesis I re-estimate the models and interact each explanatory variable with a dummy variable (INELASTIC) for whether the state is supply-constrained or not:
where all the variables are as before, except the inclusion of the dummy variable INELASTIC which takes the value of one if the state is constrained and is zero otherwise. A state is assumed to be supply-constrained if the Saiz elasticity index is below the median value of 2.1 (measured at the state level). The results of estimating these equations are shown in Table 5.
The results are consistent with the hypothesis that interest rates have a stronger effect on the housing capital income share in supply-constrained areas. In particular, the estimates in column 1 indicate that a 100 basis point decline in nominal interest rates is associated with the housing capital income share rising by about 21.6 basis points in the ‘elastic states’ and by 32.1 basis points in the ‘inelastic states’. Moreover, this difference in the sensitivity of the two types of states is statistically significant. The estimates in column 2 suggest that a 100 basis point decline in real interest rates is associated with a 22.5 basis point rise in the housing capital income share in the elastic states and a 29.4 basis point increase in the inelastic states. This difference is again statistically significant. A fall in inflation of 1 percentage point is associated with a rise in the housing capital income share of 21.8 basis points in the supply-constrained states, on average. In contrast, the effect of disinflation is estimated to be insignificant in the elastic states.
Similar patterns emerge when looking at the effects of interest rates on net profits going to home owners (columns 3 and 4) and to landlords (columns 5 and 6). In general, the negative effect of interest rates is stronger in the supply-constrained states and this negative effect reflects a combination of both real interest rates and inflation.
| Net housing capital income | Net owner-occupied housing profits | Net tenant-occupied housing profits | ||||||
|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |||
| Interest rate | −0.216* (−1.73) |
0.042* (1.87) |
−0.048*** (−3.82) |
|||||
| INELASTIC × interest rate |
−0.105** (−2.37) |
−0.044*** (−4.19) |
−0.023*** (−4.81) |
|||||
| Real interest rate | −0.225* (−1.77) |
0.042* (1.78) |
−0.049*** (−3.80) |
|||||
| INELASTIC × real interest rate |
−0.069* (−1.74) |
−0.046*** (−4.42) |
−0.022*** (−4.41) |
|||||
| CPI inflation | −0.069 (−0.43) |
0.022 (0.75) |
−0.033** (−2.42) |
|||||
| INELASTIC × CPI inflation |
−0.149*** (−2.69) |
−0.045*** (−3.97) |
−0.026*** (−4.74) |
|||||
| Housing price growth | −0.001 (−0.07) |
−0.021 (−1.06) |
0.001 (0.54) |
0.002 (0.61) |
−0.006 (−1.42) |
−0.007* (−1.79) |
||
| INELASTIC × housing price growth |
−0.022 (−1.26) |
−0.002 (−0.12) |
−0.003 (−0.96) |
−0.002 (−0.77) |
0.002 (0.59) |
0.003 (0.99) |
||
| Real GDP growth | −0.052*** (−3.17) |
−0.051*** (−3.36) |
−0.007* (−1.82) |
−0.007* (−1.75) |
−0.003 (−0.85) |
−0.003 (−0.86) |
||
| INELASTIC × real GDP growth |
0.024 (1.17) |
0.015 (0.73) |
0.008** (2.19) |
0.007** (2.06) |
0.003 (0.72) |
0.002 (0.57) |
||
| Population growth | −0.186** (−2.50) |
−0.182** (−2.46) |
−0.028 (−1.11) |
−0.028 (−1.11) |
0.049 (1.54) |
0.049 (1.54) |
||
| INELASTIC × real GDP growth |
0.140 (1.43) |
0.137 (1.36) |
−0.026 (−0.63) |
−0.024 (−0.58) |
−0.044 (−1.36) |
−0.045 (−1.37) |
||
| State fixed effects | Yes | Yes | Yes | Yes | Yes | Yes | ||
| Time fixed effects | Yes | Yes | Yes | Yes | Yes | Yes | ||
| R2 | 0.367 | 0.376 | 0.942 | 0.943 | 0.662 | 0.663 | ||
| Observations | 1,714 | 1,714 | 1,714 | 1,714 | 1,714 | 1,714 | ||
| Notes: Standard errors are clustered by state; the sample period is that underpinning the regression estimates, which covers the years from 1978 to 2012; ***, **, and * denote significance at the 1, 5 and 10 per cent level, respectively; t statistics in parentheses | ||||||||
Footnotes
This is a simplistic description of the user cost model. I ignore various complications associated with, for example, the tax deductibility of mortgage interest payments in the United States. I have estimated similar models that allow mortgage interest payments to be tax deductible (based on state-level information provided by the National Bureau of Economic Research's TAXSIM model). The TAXSIM model calculates federal and state income tax liabilities for each state and year from survey data. Based on this, it is possible to construct after-tax estimates of mortgage interest rates. However, these estimates complicate the interpretation of the models without adding much intuition. Saying that, the results are available upon request. [10]
The main regression results are not affected if I include additional state-level demographic controls such as the average household size and the age composition of the population. These results are available upon request. [11]
The model has also been estimated with quadratic time trends. The estimates are very similar to those of the model that includes the federal funds rate. [12]
The inclusion of year fixed effects in the specification for owner-occupier profits (column 6) results in the negative relationship between interest rates and profits being statistically insignificant at conventional levels. This is because there is more year-to-year variation in owner-occupier profits than in housing capital income and this variation is soaked up by the time dummies. [13]
Specifically, I assume the real interest rate (RINTRATE) is equal to the nominal interest rate (INTRATE) less CPI inflation (ΔCPI) divided by 1 plus CPI inflation. [14]
Disinflation facilitates an expansion of credit to the extent that the binding credit constraint is serviceability (the ratio of mortgage repayments to income) rather than leverage (the ratio of mortgage debt to home purchase price). See Ellis (2005) for more details. [15]
In Appendix C, I exploit a natural experiment based on the removal of interstate bank branching laws to provide more direct evidence that financial deregulation contributed to the secular rise in the share of housing capital income. [16]