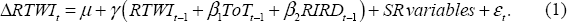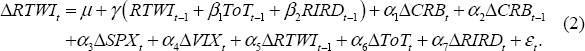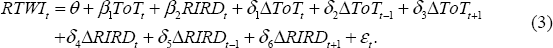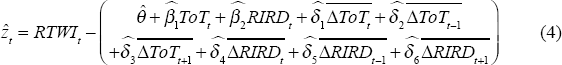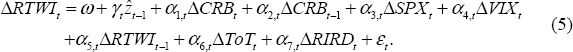RDP 2015-12: Modelling the Australian Dollar 3. The Baseline ECM
October 2015 – ISSN 1448-5109 (Online)
- Download the Paper 1.39MB
The baseline ECM is specified to address the following question:
What is the level of the exchange rate that would be expected to prevail over the medium term based on the exchange rate's historical relationships with other theoretically and empirically relevant variables?
Consistent with the literature's approach to modelling commodity currencies, this model is best described as a BEER model. BEER models are particularly suited to answering the above question as they model the exchange rate as a function of the observed values of relevant economic variables. Nevertheless, it is important to reiterate that this type of model does not attempt to directly estimate the level of the exchange rate that is consistent with desired economic outcomes.
The baseline model is similar to the specification used in Stone et al (2005), which, in turn, was based on Beechey et al (2000).[8] The model is an error correction model (ECM) of the RTWI, which estimates an equilibrium relationship between the (log) RTWI, the (log) goods ToT, and a real interest rate differential (RIRD) which is measured as the real policy rate differential between Australia and G3 economies:
The estimated equilibrium RTWI is the level that the model indicates is consistent with the level of the medium-term determinants (i.e. the ToT and the RIRD) and which should, based on relationships observed in the sample period, exert itself over time. The rate at which the RTWI is expected to converge to this equilibrium is indicated by the speed-of-adjustment coefficient, γ (also known as the error correction coefficient).
The estimation uses a single equation, rather than a system of equations for each of the cointegrating variables. While this can lead to a loss of efficiency in estimation and make it difficult to interpret the estimated cointegrating relationship, Johansen (1992) suggests the single equation approach is equivalent to the system of equations approach as long as there is only one cointegrating relationship between the variables and all other variables are weakly exogenous with respect to the parameters of the cointegrating relationship (in the sense of Engle, Hendry and Richard (1983)). Robustness tests suggest that both of these conditions are likely to hold in the context of this particular model, as well as for the various extensions presented later.[9]
As the variables in the cointegrating relationship are the determinants of the model-implied ‘equilibrium’ RTWI, it is important that their inclusion can be justified on theoretical and empirical grounds. A model that fits the data well, but makes no theoretical sense, is of limited usefulness for policy purposes as it provides no insight into the drivers of the exchange rate. The same can be said of a model that is theoretically justified, but does not perform well empirically. Discussions of the justifications for including the ToT and the RIRD follow in Sections 3.1 and 3.2.
The model also includes a number of additional variables (denoted SRvariables in Equation (1)), which are incorporated to account for shorter-term influences on the exchange rate. Specifically, the cointegrating variables are also included as changes (as opposed to just levels) in order to account for dynamic effects and potential serial correlation. Additional short-run variables also include the CRB index (a widely followed market-based commodity price measure) and two variables that are intended to capture ‘risk sentiment’ in financial markets: the (real) US S&P 500 equity index and the VIX (an index of option-implied expectations of volatility in the S&P 500). All of the short-run variables enter in first differences:
The model is focused on explaining movements in the exchange rate over the medium term. Reflecting this focus, the model is estimated at a quarterly (rather than, say, a daily) frequency, with the sample beginning in 1986.[10] This medium-term focus is also reflected in the choice of the RTWI as the exchange rate measure: a real multilateral exchange rate measure is relatively well-equipped to capture developments in Australia's external competitiveness vis-à-vis its most important trading partners.
3.1 The Terms of Trade
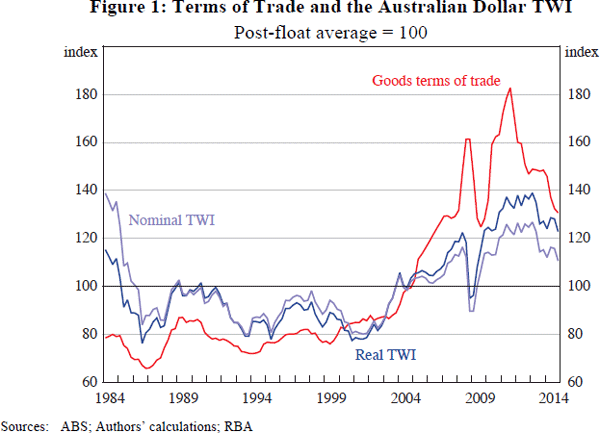
The case for including the ToT in the model is supported both by the strong empirical relationship between Australia's RTWI and ToT (Figure 1), and by the theoretical relationship between the two variables.
Regarding the theoretical relationship, the mechanisms by which the real exchange rate and the ToT are linked have been considered frequently in the literature.[11] While the exact mechanisms involved and frameworks used differ, an increase in the ToT ultimately leads to an appreciation of the RTWI because it means that domestic agents can purchase more imports in return for selling a given basket of exports. All else equal, this should be associated with a transfer of income from overseas to the domestic economy, which can, in turn, have an effect on the real exchange rate via relative price levels and/or the nominal exchange rate.
The relative price effect can arise because the additional income – and/or expectations of future sustained increases in income – stimulates domestic demand and tends to push up domestic prices and cause a real appreciation. In the literature, the increased income often enters the economy in the form of higher wages. Wages in the export sector rise due to the higher marginal product of labour associated with the higher export prices. This, in turn, pushes up wages across the rest of the economy.
The nominal exchange rate effect reflects changes in the relative demand for domestic and foreign currencies that result from the changes in the prices of exports relative to imports. For example, an increase in export prices would lead to an increase in the net demand for domestic currency. In practice, a number of factors could influence the magnitude of this channel, including the extent to which export prices are denominated in local or foreign currency, the price elasticity of foreign demand for these exports, and whether the exporters are domestically or foreign-owned.
Moreover, it should be noted that the relative price and nominal exchange rate channels will likely interact with each other. For example, a nominal exchange rate appreciation would be expected to dampen domestic demand and inflation, thereby offsetting the relative price channel to some degree. A detailed examination of the determinants of the relative importance of each channel is beyond the scope of this paper.
While the positive relationship between the RTWI and the ToT is commonly cited in the theoretical literature, it is important to note that the nature of the relationship could vary depending on the source of the ToT shock (e.g. Jääskelä and Smith 2011; Catão and Chang 2013). If the rise in the ToT reflects increased global demand – and therefore higher prices – for exports, the commonly cited positive relationship is likely to hold, although its magnitude is likely to depend somewhat on which export prices rise (Amano and van Norden 1995).
However, other shocks may lead to other dynamics. For example, the ToT could also increase in response to a positive foreign productivity shock which lowers import prices. Although in this scenario there will still be appreciation pressure stemming from the income transfer, this may be offset by Balassa-Samuelson-type effects related to the decrease in the relative productivity of the domestic economy.[12]
The fact that the RTWI may respond differently depending on the nature of the shock is likely to help explain why empirical studies have found its relationship with the ToT to be more robust for some countries than for others. In small open commodity-exporting economies, where movements in the ToT are more likely to be determined by global developments in the supply of, and demand for, their commodity exports, there is likely to be a more robust positive relationship between the RTWI and the ToT. In contrast, in economies where variation in the ToT is driven by other types of shocks, the relationship could be more varied.[13]
3.2 The Real Interest Rate Differential
While previous papers have tended to observe a significant empirical relationship between the Australian dollar RTWI and measures of the RIRD, this relationship appears to have weakened somewhat over time.[14]
Nevertheless, the uncovered interest parity (UIP) condition provides a strong theoretical basis for including the RIRD in the model. UIP states that the differential in the interest rates available in two economies for a particular time horizon should be equal to the expected future appreciation or depreciation of the exchange rate over that same horizon (abstracting from risk premiums). This ensures that the expected returns from investing in both countries are equalised, which will be associated with an ‘equilibrium’ in cross-border capital flows. However, in practice this relationship tends not to hold, which in part could reflect the fact that investors may require a (time-varying) risk premium to be willing to invest in foreign assets.
Abstracting from this premium, an increase in domestic interest rates should, all else equal, be associated with an initial appreciation of the exchange rate, though this will be offset by expectations of a larger future depreciation (or smaller appreciation) than previously expected. This initial appreciation occurs because the increase in domestic interest rates should attract additional capital from overseas, creating additional demand for the domestic currency and, therefore, pressure for the nominal exchange rate to appreciate.
3.3 Model Estimates
The model is estimated using a ‘one-step’ autoregressive distributed lag (ADL) specification, which means that the equilibrium relationship and short-run dynamics are estimated concurrently. This provides direct estimates of the speed-of-adjustment coefficient, but estimates of the coefficients and standard errors on the cointegrating variables (i.e. the βs in Equation (2)) have to be obtained using the Bewley (1979) transformation.
This approach is used instead of other alternative approaches, such as: the two-step Engle and Granger (1987) approach; the dynamic ordinary least squares (DOLS) estimator of Stock and Watson (1993); and the fully modified least squares approach of Phillips and Hansen (1990). The rationale for this choice is that the one-step approach is likely to be more appropriate in cases where the cointegrating variables are not truly non-stationary, but are instead just highly persistent, given the fact that stationary and non-stationary variables are treated similarly in the model. This may be the case for a number of the variables considered in this paper, in particular, the RIRD. Moreover, Monte Carlo simulations in a number of papers have found that the one-step approach has better small sample properties (e.g. Banerjee et al 1986; Pesaran and Shin 1999; Panopoulou and Pittis 2004; Forest and Turner 2013).[15]
Table 1 contains the results obtained when the baseline model is estimated over a sample beginning in 1986 and ending in 2014. The estimated speed-of-adjustment coefficient is somewhat smaller (in absolute terms) than previously reported, suggesting that the RTWI does not revert towards its equilibrium level as quickly as suggested by previous studies. The estimated coefficient on the ToT is similar to that reported in Stone et al (2005), although it is somewhat smaller than that reported in Beechey et al (2000). Meanwhile, the estimated coefficient on the RIRD is broadly similar in magnitude to those reported in the two earlier papers, but is now only statistically significant at the 10 per cent level.
| Variables | |
|---|---|
| Constant (μ) | 0.41*** (0.11) |
| Speed-of-adjustment (γ) | −0.22*** (0.05) |
| Equilibrium relationships | |
| Terms of trade (β1) | 0.59*** (0.05) |
| Real interest rate differential (β2) | 1.62* (0.92) |
| In-sample fit statistics | |
| R2 | 0.54 |
| Adjusted R2 | 0.49 |
| Out-of-sample forecast statistics (p-values)(a) | |
| Clark-West bootstrapped | |
| One-quarter horizon | 0.04 |
| Four-quarter horizon | 0.09 |
| Sixteen-quarter horizon | 0.20 |
| Diebold-Mariano bootstrapped | |
| One-quarter horizon | 0.00 |
| Four-quarter horizon | 0.01 |
| Sixteen-quarter horizon | 0.12 |
|
Notes: The equation is estimated by ordinary least squares using quarterly data;
***, ** and * denote significance at the 1, 5 and 10 per cent levels, respectively;
standard errors are reported in parentheses (a) H0: forecast equivalence to a random walk; calculated using rolling windows |
|
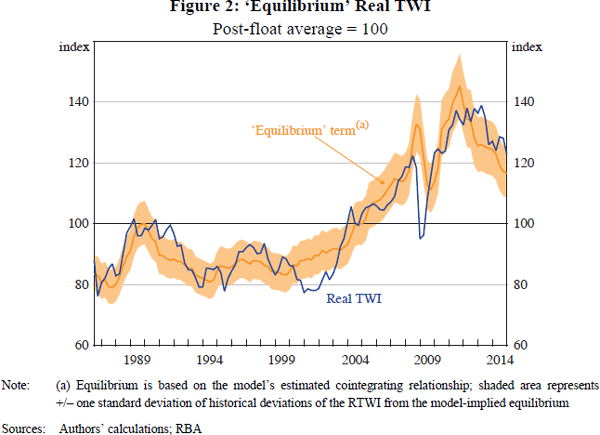
Overall, the model explains around 50 per cent of the variation in the quarterly changes in the RTWI over the sample period. Although there have been episodes of unusually large or sustained divergences between the observed RTWI and the estimated equilibrium level within the sample period, in most cases these reflect the short-run dynamics of the model, rather than the model residuals (Figure 2). Consequently, previous attempts to find variables other than the ToT (and the RIRD) that consistently explain medium-term movements in the RTWI have been largely unsuccessful.
While neither the baseline model nor any of the variants described in this paper are used for forecasting purposes, their out-of-sample performance can still be used to assess the robustness of their explanatory power.[16] This is because a robust model of the exchange rate should, in general, embed enough information about the relationship between the exchange rate and its determinants to produce reasonable forecasts. Based on Clark and West (CW) and Diebold and Mariano (DM) statistics, the baseline model produces more accurate forecasts than a naïve random walk model at one-quarter horizons (more details are available in Appendix A). There is also some evidence to suggest that the model produces more accurate forecasts at the four-quarter and sixteen-quarter horizons, though care should be taken in interpreting these results as it is possible that the explanatory variables are not ‘strongly exogenous’ in the sense of Engle et al (1983).[17]
Still, there have been some episodes since 1986 when the model's (short-run) residuals have accounted for a relatively large share of the (medium-run) divergence between the observed RTWI and the model's estimated equilibrium. Relatedly, in previous RBA papers, which are generally estimated over shorter sub-periods, some additional medium-term variables have been found to be significant determinants of the RTWI. This suggests that there may be some relevant variables that are omitted from the model as it is currently specified (potentially because they have not had a sufficiently consistent effect on the exchange rate over the entire post-1986 period), but which may nevertheless have affected the exchange rate at different points in time. This could reflect the possibility that some of these variables have always been relevant, but have only exerted an identifiable effect on the RTWI during certain sub-periods, or, alternatively, it could simply reflect the fact that financial market participants often appear to focus on different variables at different points in time (Debelle and Plumb 2006).
For example, during the information technology boom in the early 2000s the RTWI remained persistently below the estimated equilibrium level, apparently reflecting investors' strong preferences during this episode for currencies that were aligned with so called ‘new’ economies (which did not include Australia). Similarly, during the early stages of the global financial crisis in 2008, the RTWI depreciated sharply – reflecting the heightened level of risk and the global shortage of US dollars – while the estimated equilibrium term (and the ToT) remained at a high level. More recently, in 2010–11, the RTWI was somewhat below its estimated equilibrium level, while in 2012 and early 2013 the RTWI remained high relative to its estimated equilibrium level. This continued throughout much of 2014.
While it is possible to incorporate some of these factors by adding dummy variables to the model ex post, as in Stone et al (2005), such an exercise is less useful when trying to understand developments in the Australian dollar on an ongoing basis. Instead, it may be preferable to consider extensions which allow the estimated parameters to vary over time (considered in Sections 3.4 and 4), or which augment the model with additional theoretically relevant variables that capture these potential omitted influences directly (considered in Sections 5 and 6).
3.4 A Rolling Error Correction Model
A simple way of allowing the model's estimated parameters to vary is to estimate rolling regressions. This approach takes an agnostic view of whether, and what, additional factors may be influencing the RTWI at any point in time. Such an approach can also be seen as a robustness test for the model, as a high degree of instability would suggest the model is poorly specified.
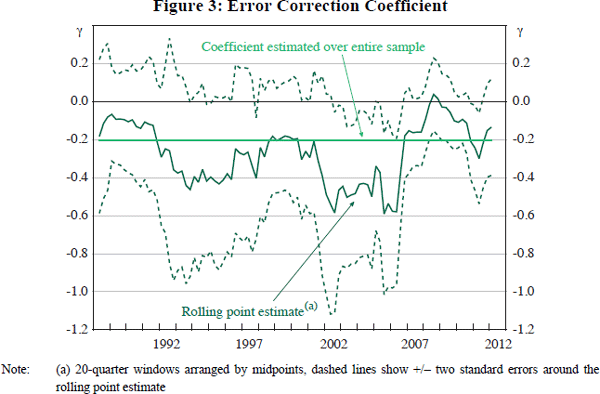
Given that a key requirement of any ECM is a stable cointegrating relationship between the long-run variables, we focus on changes in the short-run dynamics of the model while keeping the cointegrating relationship stable. In this regard, particular attention is paid to the estimated speed-of-adjustment coefficient as it enables some judgements to be made about changes in the RTWI's behaviour around the estimated equilibrium.[18] If the magnitude of the coefficient is smaller, it suggests that the exchange rate adjusts towards its equilibrium more slowly and deviations will tend to be more persistent. In other words, persistent – but not directly observable – shocks to the RTWI can be represented as a change in the regime governing the error correction term.
To examine changes in the speed-of-adjustment coefficient, a rolling ECM can be estimated using a two-step procedure which holds the long-run relationship constant while allowing the short-run dynamics to vary over time. More specifically, the cointegrating relationship can first be estimated over the entire sample period using DOLS (Stock and Watson 1993):[19]
The deviation from the ‘estimated’ equilibrium from this model can then be calculated as:
where the bars reflect averages over the sample.
The deviations from the estimated equilibrium (ẑt), lagged by one quarter, can then be used to estimate a short-run model in differences over rolling samples:
To examine how the speed-of-adjustment coefficient (γt) evolves over time, 95 separate regressions were generated using 20-quarter windows between 1986:Q2 and 2014:Q3.[20]
The rolling point estimates of the speed-of-adjustment coefficient (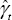 )
have varied somewhat and, as expected, the adjustment appears to have been
somewhat slower (
)
have varied somewhat and, as expected, the adjustment appears to have been
somewhat slower (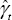 has been less negative) during periods when
the RTWI has diverged persistently from the estimated equilibrium (particularly
following the global financial crisis;
Figure 3).[21]
Nevertheless, given the wide error bands, the rolling ECM does not provide
substantial evidence of changes in the RTWI's rate of reversion back to
the estimated
equilibrium.[22]
has been less negative) during periods when
the RTWI has diverged persistently from the estimated equilibrium (particularly
following the global financial crisis;
Figure 3).[21]
Nevertheless, given the wide error bands, the rolling ECM does not provide
substantial evidence of changes in the RTWI's rate of reversion back to
the estimated
equilibrium.[22]
Footnotes
Nevertheless, there are a few small differences. Most notably, the dummy variable – which was included in the Stone et al (2005) model to account for a sustained period of divergence between the RTWI and the ToT in the late 1990s and early 2000s – is no longer included. [8]
Johansen tests of cointegration suggest that there is only one cointegrating relationship for the baseline model and the extensions presented in this paper. Regarding weak exogeneity, a number of papers have noted that the ToT may not be weakly exogenous with respect to the RTWI, reflecting gradual nominal price adjustments and incomplete pass through of exchange rate movements (e.g. Chen and Rogoff 2003). Stone et al (2005) note that these issues are more likely to be evident in services trade and so use the goods ToT, in place of the goods and services ToT, in modelling the Australian dollar. We follow their methodology. Formal tests performed using a vector error correction model approach also suggest that the cointegrating variables (other than the RTWI) are weakly exogenous. Again this is true for both the baseline model and the other models that are subsequently presented in this paper. [9]
A longer sample is not used as prior work by the RBA has suggested that the behaviour of the exchange rate changed somewhat after the Australian dollar was floated in 1983. The exact choice of start date also reflects the availability of data for some of the explanatory variables. [10]
For example, Blundell-Wignall and Gregory (1990), Blundell-Wignall et al (1993), Dwyer and Lowe (1993), Chen and Rogoff (2003), and Cashin et al (2004) all provide explanations for why an increase in the ToT should be associated with an appreciation of the real exchange rate. For intuitive treatments which also discuss the nominal exchange rate's response, see Connolly and Orsmond (2011), Plumb, Kent and Bishop (2013), Stevens (2013) and Kent (2014). [11]
For a detailed exposition, see, for example, Obstfeld and Rogoff (1996, ch 4). [12]
This is despite the fact that both the real exchange rate and the ToT represent the relative prices of baskets of domestic and foreign goods and so should be expected to move together mechanically to some degree. [13]
This is mainly true for the real (short-term) policy rate differential, rather than necessarily for longer-term RIRDs. For a more detailed discussion of the relative merits of using RIRDs based on short- and/or longer-term interest rates, see Section 6. [14]
It should be noted that there is still likely to be some bias in the estimates of the βs, given that they are not estimated directly but are instead calculated as the ratio of other estimated coefficients. [15]
While this approach is common in the literature on exchange rate modelling, Diebold (2015) criticises the use of pseudo-out-of-sample forecast comparisons for this purpose. [16]
Strong exogeneity is necessary when forecasting more than one step ahead using a single equation, rather than a system of equations. Some papers have tentatively suggested that the ToT and the RIRD are not Granger-caused by the RTWI, and so are strongly exogenous (see, for example, Stone et al (2005) for the ToT, and Lubik and Schorfheide (2007) for nominal interest rates). Granger-causality tests conducted for this paper suggest that this is the case for the ToT, though the results for the RIRD are less clear. [17]
While changes in the coefficients on the short-run variables – particularly on the lagged change in the RTWI – can also suggest changes in the behaviour of the exchange rate around its estimated equilibrium, illustrative analysis suggests these considerations are likely to be of second order. [18]
Leads and lags were chosen based on the Schwarz criterion. Newey-West heteroskedasticity and autocorrelation robust standard errors are used. [19]
Although an intercept (ω) is included in the short-run Equation (4), implying a trend in the RTWI's behaviour around the estimated equilibrium, in practice the estimated coefficient is close to zero. [20]
The error correction term estimated using DOLS is slightly less negative than that estimated using the ADL specification. [21]
Different window lengths were tested with similar results. Moreover, rolling point estimates of the coefficients on the short-run variables also fail to provide substantial evidence of changes. [22]