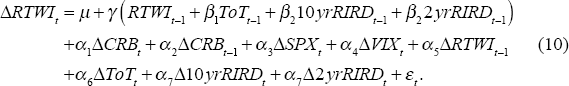RDP 2015-12: Modelling the Australian Dollar 6. Incorporating Unconventional Monetary Policy
October 2015 – ISSN 1448-5109 (Online)
- Download the Paper 1.39MB
In addition to the resources boom, another recent macroeconomic development that may help to identify additional relevant explanatory variables has been the implementation of unconventional monetary policy by a number of major advanced economy central banks – including quantitative easing and explicit forward guidance. A key objective of these actions has been to lower longer-term bond yields as policy rates have approached (and even moved slightly below) zero. This objective appears to have been met; for example, a GDP-weighted average of real yields on US, Japanese and German 10-year government securities declined by around 200 basis points between mid 2009 and end 2014, whereas a similar measure constructed using real policy rates was broadly unchanged over the same period (Figure 13).
In addition to the effect of unconventional monetary policy on longer-term bond yields in the countries concerned, a number of papers have documented the influence of these actions on global asset prices.[40] Of particular interest, Bauer and Neely (2014) and Neely (2014) find evidence that the US Federal Reserve's unconventional monetary policy actions led to lower yields on Australian Government securities (AGS) and to an appreciation of the Australian dollar against the US dollar.
The papers usually point to two main channels through which these effects are propagated:
- the signalling channel, which operates via the effect of unconventional monetary policy on the market's expected future path of (domestic and, potentially, foreign) short-term interest rates;
- the portfolio balance channel, which operates via the effect of central bank asset purchases on the prices of those assets. This can lead investors to substitute towards alternative assets, including foreign assets, in turn pushing up a broader range of asset prices. If this substitution involves cross-border capital flows, there can be implications for exchange rates.
However, the baseline ECM of the RTWI is unlikely to adequately capture these dynamics. This is because the model's RIRD variable is based on policy rates, whereas unconventional monetary policy is more likely to be evident through its effect on longer-term interest rates. In an attempt to better capture these dynamics, we present a number of augmented versions of the existing model that incorporate alternative RIRD measures.[41] To this end, two model variations are presented: (i) models that replace the real policy rate differential variable with a longer-term RIRD (Section 6.1); and (ii) models that include information on both short- and long-term RIRDs (Section 6.2). Importantly, only specifications that can be estimated over the same sample period as the existing model are considered (1986 onward). Consequently, a number of alternative RIRD measures – particularly those based on measures of expected inflation – are excluded owing to data availability constraints.
Although a range of interest rates could be used to calculate longer-term RIRDs, we focus on 10-year yields on government securities for consistency with previous work. The results are nevertheless broadly similar if government debt securities of shorter maturities are used instead (e.g. 2-year or 5 year tenors), and if government bond yields are replaced with swap rates. A more fundamental issue, though, is the choice of which inflation measure to use to deflate nominal yields. When assessing investments, the relevant consideration for forward-looking market participants is expected inflation over the investment horizon. Nevertheless, past papers have tended to use observed inflation over the previous year, which implicitly assumes that inflation expectations are highly adaptive (Gruen and Wilkinson 1991; Blundell-Wignall et al 1993). Although inflation over the previous year could be a reasonable measure of inflation expectations for the near-term – and could therefore be deemed an acceptable deflator for short-term interest rates – it is less likely to reflect inflation expectations over longer horizons.
To address this, a ‘forward-looking’ 10-year RIRD measure is also constructed. This measure uses expectations implied by 10-year inflation-linked government securities as the measure of Australian inflation expectations, and the Federal Reserve Bank of Cleveland's survey-based measure of expected inflation over the next 10 years as the measure of US inflation expectations.[42]
6.1 Policy Rates and Longer-term Rates
Past RBA work has found RIRDs based on longer-term interest rates to be significant determinants of the RTWI, (Gruen and Wilkinson 1991; Blundell-Wignall et al 1993). This is consistent with the forward-looking nature of foreign exchange markets. For example, assuming that the expectations hypothesis holds, if market participants believe that a country's central bank has shifted to an easing bias and will soon begin to reduce its policy rate, longer-term rates should decline and the exchange rate would generally be expected to depreciate even though the observed policy rate will initially remain unchanged.
To examine this, models which include 10-year RIRD measures instead of the real policy rate differential were estimated. The results are not reported as the estimated coefficients on the 10-year RIRD measures are negative and statistically insignificant, which is counterintuitive.
One possible explanation for the unexpected negative (and insignificant) coefficients could be the presence of time-varying sovereign ‘risk premia’, which also affect the exchange rate.[43] A decline in such a premium is tantamount to an outwards shift in the demand curve for government debt in that, all else equal, it would lead to higher prices, lower yields and therefore a lower RIRD. However, this lower RIRD is unlikely to be associated with a depreciation of the exchange rate. In fact, if the decline in the risk premium entices foreign investors to purchase additional securities (or domestic investors to shift from foreign to domestic securities) the lower RIRD could even be associated with a local currency appreciation.
This type of dynamic may have been evident in Australia in recent years, as foreign investors have increased their holdings of AGS.[44] Further, it is broadly consistent with the portfolio balance channel of unconventional monetary policy transmission. If such a dynamic has been at play, it will make it more difficult to identify a stable relationship between longer-term RIRDs and the exchange rate. For example, a given increase in the RIRD could reflect either an increase in the risk premium (which would be expected to be associated with, if anything, a depreciation of the RTWI) or an increase in expected interest rates (which would be expected to be associated with an appreciation of the RTWI), or a combination of the two.
6.2 Long- and Short-term Real Interest Rate Differentials
Tarditi (1996) suggests that interest rate differential measures that are based on the slopes of yield curves are likely to provide more explanatory power than measures that are based only on short- or longer-term interest rates. This is because the slope of the yield curve captures both the current stance of monetary policy and the anticipated path of future short-term rates. To examine this, we estimated a number of models that include nominal and real slope differentials instead of the real policy rate differential. Consistent with Tarditi (1996), the estimated coefficients on the slope differentials were negative and statistically significant in all variations. This suggests that a flattening of the Australian yield curve relative to the foreign yield curve has – over the medium term – been associated with an appreciation of the RTWI. Nevertheless, the results are difficult to interpret because changes in the slope of the yield curve can be driven by movements in shorter- and/or longer-term interest rates, with quite different implications for the RTWI depending on the relative contributions of each.
To address this, short- and long-term real rate differentials can instead be allowed to enter the model separately. This can be interpreted as allowing changes in current and/or expected short-term interest rates (proxied using the 2-year government bond yield differential) and in risk premiums (proxied using longer-term rate differentials) to affect the RTWI in different ways. It can also be thought of as allowing the model to separately incorporate the influence of unconventional monetary policy that is transmitted via the signalling channel – often identified in the literature using shorter-term rates – and via the portfolio balance channel – often identified in the literature using longer-term rates (e.g. Rogers et al 2014).
Two specifications are reported. The first – which is subsequently referred to as the ‘backward-looking' model – includes the 10-year RIRD between Australia and the G3 economies and the 2-year RIRD between Australia and the G3, with all rates deflated using the prior year's inflation rate. The second – subsequently referred to as the ‘forward-looking’ model – includes the 10-year RIRD between Australia and the United States, deflated using measures of inflation expectations, and the 2-year rate differential between Australia and the United States, deflated using previous-year inflation:[45]
The results are reported in Table 5.[46] To summarise, the coefficient on the 2-year rate differential is positive and significant in both models, while the coefficient on the 10-year rate differential is negative and significant. The fact that the coefficients on the individual 2-year and 10-year rate differentials become significant when both variables are included in the model suggests that there may be an omitted variable bias in the models that include only one of the variables. Meanwhile, the in-sample and out-of-sample fits of the models with two RIRD variables are similar to that of the baseline model.
| Baseline | Backward-looking | Forward-looking | |
|---|---|---|---|
| Variables | |||
| Constant | 0.41*** (0.11) |
0.40*** (0.12) |
0.44*** (0.12) |
| Speed-of-adjustment | −0.22*** (0.05) |
−0.19*** (0.05) |
−0.22*** (0.05) |
| Equilibrium relationships | |||
| Terms of trade | 0.59*** | 0.52*** | 0.57*** |
| (0.05) | (0.06) | (0.05) | |
| Real interest rate differential – short-term | 1.62* (0.92) |
6.87** (3.18) |
1.35* (0.76) |
| Real interest rate differential – long-term | −7.38* (3.37) |
−4.63*** (2.31) |
|
| In-sample fit statistics | |||
| R2 | 0.54 | 0.55 | 0.53 |
| Adjusted R2 | 0.49 | 0.50 | 0.49 |
| Out-of-sample forecast statistics(a) | |||
| Clark-West bootstrapped | |||
| One-quarter horizon | 0.04 | 0.05 | 0.07 |
| Four-quarter horizon | 0.09 | 0.10 | 0.12 |
| Sixteen-quarter horizon | 0.20 | 0.21 | 0.28 |
| Diebold-Mariano bootstrapped | |||
| One-quarter horizon | 0.00 | 0.00 | 0.00 |
| Four-quarter horizon | 0.01 | 0.03 | 0.03 |
| Sixteen-quarter horizon | 0.12 | 0.10 | 0.19 |
|
Notes: The equation is estimated by ordinary least squares using quarterly data;
***, ** and * denote significance at the 1, 5 and
10 per cent levels, respectively; standard errors are reported in
parentheses (a) H0: forecast equivalence to a random walk; calculated using rolling windows |
|||
It is worth noting that the high degree of positive correlation between the 2-year and 10-year rates means that the estimates of these coefficients are likely to be affected by collinearity, which makes it difficult to interpret the individual coefficients. In turn, this may help to explain the relatively large magnitudes of the two estimated RIRD coefficients. However, given the estimated coefficients have opposite signs, the model will net off the two effects when estimating the overall impact of interest rates on the equilibrium RTWI.
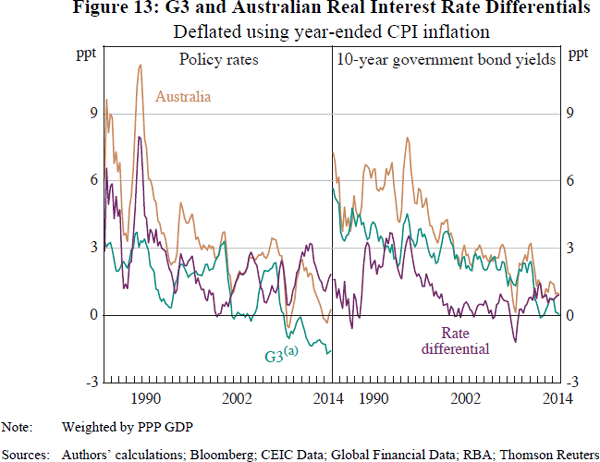
The estimated equilibrium terms from both the backward- and forward-looking models are also similar to the baseline model's estimated equilibrium (Figure 14). However, the estimated equilibrium from the forward-looking model has been a bit higher than the equilibrium from the baseline model in recent years, and has therefore tended to track movements in the observed RTWI somewhat more closely over this period. While this provides some tentative evidence that unconventional monetary policy in the major advanced economies has had some effect on the RTWI over recent years, it does not result in a significant improvement in the overall fit of the model over the entire sample period.
Footnotes
See for example: Bauer and Neely (2014); Neely (2014); Rogers, Scotti and Wright (2014); and Bowman, Londono and Sapriza (2014). [40]
One other approach that was considered, but which is not reported in detail as the estimated coefficient was not significant, is to use ‘shadow rates’, as reported in Wu and Xia (2014), in place of policy rates. Shadow rates are estimates of the short-term rate that would be associated with the stance of monetary policy, if the zero lower bound was not binding. [41]
Liquidity and other issues in the market for Australian inflation-linked government securities could distort the measure of inflation expectations. However, an alternative measure is not available over a sufficient sample. Further, while there could be issues in comparing a market-implied measure (as used for Australia) with a survey measure (as used for the United States), a sufficient time series on US inflation-linked securities was not available. Adequate time series data on Japanese and German inflation expectations are also not available. [42]
Kaminska, Meldrum and Smith (2013) find that a time-varying ‘foreign exchange risk premium’ plays a role in determining exchange rates. In this paper, ‘risk premiums’ is a broad term that encompasses a number of factors, including term premiums and credit spreads. These factors are influenced both by investor expectations and changes in investors' preferences and/or risk aversion. [43]
Models that directly incorporate foreign holdings of AGS were also considered. Neither the level of, nor the change in, foreign holdings of AGS were found to be significant determinants of the RTWI. [44]
The 2-year rate is used instead of the policy rate as it is deemed to be more likely to capture the ‘signalling’ channel. [45]
Unit root tests indicate that the 2-year and 10-year RIRDs are non-stationary over the sample period. [46]